25 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Số phức nâng cao-P1 (có đáp án)

Câu 1:

Cho hai số phức z₁; z₂ khác 0 thỏa mãn $z_{1}^{3} + z_{2}^{3} = 0$ .Gọi A; B lần lượt là các điểm biểu diễn cho số phức z₁; z₂. Khi đó tam giác OAB là:

A. Tam giác đều.

B. Tam giác vuông tại O.

C. Tam giác tù.

D. Tam giác có một góc bằng 45^o.

Xem đáp án

Chọn A.

Ta có ,

suy ra:

Lại có

nên

Suy ra AB = OA= OB

Do đó. Tam giác OAB là tam giác đều.

Câu 2:

Cho số phức z thỏa mãn $(2 z - 1) (1 + i) + (\bar{z} + 1) (1 - i) = 2 - 2 i$ . Giá trị của |z| là ?

A. $\frac{\sqrt{2}}{3}$

B. 2.

C. $\frac{\sqrt{3}}{2}$

D. $\frac{\sqrt{2}}{2}$

Xem đáp án

Chọn A.

Gọi z = a + bi ta có :

Câu 3:

Cho số phức z = a + bi thỏa mãn .Tính P = a + b

A. -3.

B. -1.

C. 1.

D. 2.

Xem đáp án

Chọn C.

Đặt z = a + bi.

Theo giải thiết ta có:

[(a + 1) + (b + 1)i](a - bi - i) + 3i = 9

Suy ra : a( a + 1) + ( b + 1) ²+ a( b + 1) i - ( a + 1) ( b + 1) i = 9 - 3i

Hay a(a + 1) + ( b + 1) ²- ( b +1) i = 9 -3i

Ta có hệ

Do nên a = -1; b = 2

Vậy P = a + b = 1.

Câu 4:

Số nghiệm của phương trình với ẩn số phức z: 4z² + 8|z|² - 3 = 0 là:

A. 3.

B. 2.

C. 4.

D. 1.

Xem đáp án

Chọn C.

Gọi z = a + bi là nghiệm của phương trình.

Ta có: 4(a + bi) ²+ 8(a²+ b²) - 3 = 0

$\Leftrightarrow$ 4(a² – b²+ 2abi) + 8( a²+ b²) - 3 = 0

$\Leftrightarrow$ 12a²+ 4b²+8abi - 3 = 0

$\Leftrightarrow \{\begin{cases} [\begin{matrix} a = 0 \\ b = \pm 1 \end{matrix} \\ [\begin{matrix} a = \pm \frac{1}{2} \\ b = 0 \end{matrix} \end{cases}$

Vậy phương trình có 4 nghiệm.

Câu 5:

Gọi z₁; z₂; z₃; z₄ là các nghiệm phức của phương trình .

Giá trị của là:

A. 17/8

B. 17/9

C. 9/17

D. 17i/9

Xem đáp án

Với mọi z ≠ i/2, ta có:

Câu 6:

Cho số phức z; w thỏa mãn |z – 1 + 2i| = |z + 5i| ; w = iz + 20. Giá trị nhỏ nhất m của |w| là?

Xem đáp án

Chọn B.

Gọi z = x + yi thì M(x; y) là điểm biểu diễn z.

Gọi A(1; -2) và B(0; -5), ta có tập hợp các điểm z thỏa mãn giả thiết đề bài là đường trung trực của AB có phương trình ∆: x + 3y +10 = 0.

Ta có |w| = |iz + 20| = |z – 20i| = CM với M là điểm biểu diễn số phức z và C(0; 20) .

Do đó

Câu 7:

Xét các số phức z thỏa mãn thiết | z + 2 - i| + | z - 4 - 7i|= $6 \sqrt{2}$ . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của |z – 1 + i|. Tính P = m + M.

Xem đáp án

Chọn B.

Ta có:

Suy ra:

Xét điểm A(-2; 1) và B(4; 7) , phương trình đường thẳng AB: x - y + 3 = 0.

Gọi M(x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.

Khi đó ta có và ta thấy , suy ra quỹ tích M thuộc đoạn thẳng AB.

Xét điểm C( 1; -1); ta có , hình chiếu H của C trên đường thẳng AB nằm trên đoạn AB.

Do đó

Vậy

Câu 8:

Cho số phức z thỏa mãn điều kiện |z -2 + 2i | + | z + 1 -3i | = $\sqrt{34}$ . Hãy tìm giá trị lớn nhất, giá trị nhỏ nhất của |z + 1 + i|.

A. $6 \sqrt{34} v à 8$

B. $\frac{6 \sqrt{34}}{17} v à 4$

C. $\sqrt{34} v à 8$

D. Đáp án khác.

Xem đáp án

Chọn B.

Gọi M (x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.

Gọi điểm A(2; -2) ; B(-1; 3) và C(-1; -1)

Phương trình đường thẳng AB: 5x + 3y - 4 = 0.

Khi đó theo đề bài

Ta có . Do đó quỹ tích M là đoạn thẳng AB.

Tính CB = 4 và .

Hình chiếu H của C trên đường thẳng AB nằm trên đoạn AB.

Vậy

Câu 9:

Cho số phức z thoả mãn |z – 1 + 3i| + |z + 2 – i| = 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = |2z + 1 + 2i|.

A. 8 và 4

Xem đáp án

Chọn D.

Ta có P = |2z + 1 + 2i| nên

Ta cần tìm giá trị lớn nhất, giá trị nhỏ nhất của:

Ta có z₁= 1 - 3i; z₂= -2 + i và z₀= -1/2 - i

Ta thấy:

Tính

Suy ra

Vậy Max P = 2.4 = 8 và

Câu 10:

Cho số phức z thỏa mãn |z – 2 – 3i| = 1. Tìm giá trị lớn nhất của |z|?

Xem đáp án

Chọn A.

Gọi M( x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.

Ta thấy tập hợp điểm biểu diễn của số phức z là đường tròn tâm I (2; 3) và bán kính r = 1.

Do đó . ( khi 3 điểm O; I và M thẳng hàng).

Câu 11:

Cho số phức z thỏa mãn |z – 1 – 2i| = 4. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của |z + 2 + i|. Tính S = m²+ M²?

A. 34

B. 82

C. 68

D. 36

Xem đáp án

Chọn C.

Ta có |z – 1 – 2i| = 4. Hay |z – (1 + 2i)| = 4.

Đặt w = z + 2 + i

Gọi M( x; y) là điểm biểu diễn của số phức w trên mặt phẳng Oxy.

Khi đó, tập hợp điểm biểu diễn của số phức w là đường tròn tâm I, với I là điểm biểu diễn của số phức 1 + 2i + 2 + i = 3 + 3i.

Tức là tâm I(3; 3) , bán kính r = 4.

Do đó:

Vậy S = m²+ M²= 68.

Câu 12:

Cho số phức z thỏa mãn |(1+ i )z + 1 -7i | = $\sqrt{2}$ . Tìm giá trị lớn nhất của |z|?

A. 4

B. 3

C. 7

D. 6

Xem đáp án

Chọn D.

Đặt w = ( 1 + i)z , suy ra

Gọi M( x; y) là điểm biểu diễn của số phức w trên mặt phẳng Oxy.

Khi đó tập hợp điểm biểu diễn của số phức w là đường tròn tâm I(-1; 7) , bán kính

Ta có

Vậy

Câu 13:

Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức z thỏa mãn là đường tròn C. Khoảng cách từ tâm I của đường tròn (C) đến trục tung bằng bao nhiêu?

A. d(I; Oy) = 1.

B. d(I ; Oy) = 2.

C. d(I ; Oy) = 0.

D. $d (I; O y) = \sqrt{2}$

Xem đáp án

Chọn A.

Gọi M(x; y) là điểm biểu diễn số phức z = x + yi.

Ta có:

hay ( x+ 1) ²+ y²= 9

Suy ra I(-1; 0) là tâm đường tròn (C)

Câu 14:

Số phức z thỏa mãn điều nào thì có điểm biểu diễn thuộc phần gạch chéo như trên hình.

A. Số phức z = a + bi; |z| ≤ 2; -1 ≤ a ≤ 1.

B. Số phức z = a + bi; |z| ≤ 2; a < -1; a > 1.

C. Số phức z = a + bi; |z| < 2; -1 ≤ a ≤ 1.

D. Số phức z = a + bi; |z| ≤ 2; -1 ≤ b ≤ 1.

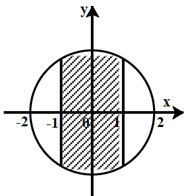
Xem đáp án

Chọn A.

+ Từ hình biểu diễn ta thấy tập hợp các điểm M(a; b) biểu diễn số phức z trong phần gạch chéo đều thuộc đường tròn tâm O(0;0) và bán kính bằng 2; ngoài ra -1 ≤ a ≤ 1.

+ Vậy M(a; b) là điểm biểu diễn của các số phức z = a + bi có mô đun nhỏ hơn hoặc bằng 2 và có phần thực thuộc đoạn [-1;1].

Câu 15:

Trong mặt phẳng phức Oxy, số phức z thỏa điều kiện nào thì có điểm biểu diễn số phức thuộc phần tô màu như hình vẽ

A. 1 ≤ |z| ≤ 2 và phần ảo dương.

B. 1 ≤ |z| ≤ 2 và phần ảo âm.

C. 1 < |z| < 2 và phần ảo dương.

D. 1 < |z| < 2 và phần ảo âm.

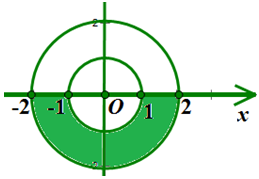
Xem đáp án

Chọn B.

Ta thấy phần tô màu là nửa dưới trục hoành của hình vành khăn được tạo bởi hai đường tròn đồng tâm O(0 ;0) và bán kính lần lượt là 1 và 2.

Vậy đây chính là tập hợp các điểm M(x; y) biểu diễn cho số phức z = x + yi trong mặt phẳng phức với 1 ≤ |z| ≤ 2 và có phần ảo âm.

Câu 16:

Cho số phức z thỏa mãn |z – 4| + |z + 4| = 10. Giá trị lớn nhất và nhỏ nhất của mô – đun của số phức z là

A. 10 và 4

B. 5 và 4

C. 4 và 3

D. 5 và 3

Xem đáp án

Chọn D.

Giả sử z = x + yi có điểm biểu diễn là M(x; y).

Giả sử F₁( 4 ; 0) ; F₂( -4 ; 0) khi đó tập hợp các điểm M thỏa mãn là MF₁+ MF₂= 10 là đường elip (E) có các tiêu điểm là F₁; F₂ và trục lớn bằng 10.

Từ đó ta tìm được 2c = F₁F₂ = 8 nên c = 4.

2a = 10 nên a = 5

suy ra b²= a²- c²= 9 nên b = 3.

Từ đó

Vì M di động trên (E) nên |z| = OM lớn nhất, nhỏ nhất khi OM lần lượt là độ dài nửa bán trục lớn, nửa bán trục nhỏ. Hay max |z| = 5 ; min |z| = 3.

Câu 17:

Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy để với số phức z có phần thực không âm. Tính diện tích hình (H).

Xem đáp án

Chọn A.

+ Giả sử z = a + bi, khi đó , giả thiết của bài toán là

+ Vậy tập hợp các điểm biểu diễn cho số phức z là điểm M(a; b) thuộc miền trong của elip (kể cả các điểm trên biên).

+ Bán trục lớn của ( E) là a = 3, bán trục bé của ( E) là b = 1 nên diện tích cần tính của miền ( H) là S = πab = 3π.

Câu 18:

Có số phức z có phần ảo bằng 164 và n ∈ R* thỏa mãn: . Tìm n?

A. 679

B. 697

C. 567

D. Đáp án khác

Xem đáp án

Chọn B.

Gọi z = a + 164i

Theo giả thiết, ta có

⇔ a + 164i = 4i(a + 164i + n)

Hay a + 164i = -656 + 4(a + n) i

(thỏa mãn)

Vậy n = 697.

Câu 19:

Tìm số phức z thỏa mãn hai điều kiện:| z + 1 - 2i| = | $\bar{z}$ + 3 + 4i| và $\frac{z - 2 i}{\bar{z} + i}$ là một số thuần ảo.

Xem đáp án

Chọn B.

Giả sử z = x + yi. Theo bài ra ta có: |x + 1 + (y – 2)i| = |x + 3 + (4 – y)i|

hay ( x + 1) ²+ ( y - 2) ²= ( x + 3) ²+ ( y - 4) ²

suy ra y = x + 5

Số phức

w là một số thuần ảo

Vậy

Câu 20:

Trong các số phức z thỏa mãn điều kiện | z - 2 + 3i | = $\frac{3}{2}$ . Số phức z có mođun nhỏ nhất có phần thực gần với giá trị nào nhất?

A. 1,17

B. 1,16

C. 1,15

D. 1,14

Xem đáp án

Chọn A.

Đặt z = x+ yi.

Khi đó

Các điểm M biểu diễn số phức z thỏa mãn hệ thức đã cho nằm trên đường tròn tâm I(2;-3) và bán kính R = 3/2.

Ta có: min|z| khi và chỉ khi M nằm trên đường tròn và gần O nhất.

Đó là điểm M₁( là giao điểm của tia IO với đường tròn) (Bạn đọc tự vẽ hình).

Ta có: . Kẻ

Theo định lý Talet ta có:

Vậy

Câu 21:

Tìm số phức z thỏa mãn (z - 1)( $\bar{z}$ + 2i) là số thực và |z| đạt giá trị nhỏ nhất.

A. z = 1+ 2i

Xem đáp án

Chọn B.

Giả sử z = x + yi. Khi đó:

Để là số thực thì ( x - 1) ( 2 - y) + xy = 0 hay 2x + y – 2 = 0.

Suy ra tập hợp các điểm M biểu diễn số phức z thỏa mãn là số thực là đường thẳng $∆$ có phương trình 2x + y - 2 = 0.

Để modul z nhỏ nhất thì M phải là hình chiếu của O ( 0; 0) lên Δ.

Từ đó tìm được nên

Câu 22:

Trong các số phức z thỏa mãn |z - 3i| + | i $\bar{z}$ + 3| =10 , tìm số phức z có mô-đun nhỏ nhất.

A. z = 2 hoặc – 2

B. z= 3 hoặc – 3

C. z = 4 hoặc – 4

D. tất cả sai

Xem đáp án

Chọn C.

Áp dụng công thức:

Ta có:

Giải bất phương trình ta có 0 ≤ |z| ≤ 4

Vậy min|z| = 4 đạt được khi

Câu 23:

Trong các số phức z thỏa mãn | z - 2 + i | = | $\bar{z}$ + 1 -4i | , tìm số phức có mô-đun nhỏ nhất.

A. z = 1

B. z = 1 - i

C. z = -1 - i

D. z = 2 - i

Xem đáp án

Chọn C.

Giả sử z = a+ bi. Khi đó:

z – 2 + i = ( a - 2) + ( b + 1) i và

$\bar{z} + 1 - 4 i = (a + 1) - (b + 4) i$

Khi đó |z| đạt giá trị nhỏ nhất khi b = -1, suy ra a = -2 - (-1) = -1

Vậy z = -1 - i thỏa mãn đề bài.

Câu 24:

Tìm giá trị lớn nhất của |z| biết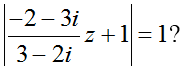

A. $\sqrt{2}$

B. 2

C. 1

D. 3

Xem đáp án

Chọn B.

Ta có

Gọi M(x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.

Khi đó tập hợp điểm biểu diễn của số phức z là đường tròn tâm I( 0; -1), bán kính r = 1.

Vậy Max|z| = OI + r = 1 + 1 = 2.

Câu 25:

Cho số phức z thỏa mãn |z – 2- 3i| = 1. Giá trị lớn nhất của là?

A. $\sqrt{13} + 2$

B. 4

C. 6

D. $\sqrt{13} + 1$

Xem đáp án

Chọn D.

Ta có

Đặt

Gọi M( x; y) là điểm biểu diễn của số phức w trên mặt phẳng Oxy.

Khi đó tập hợp điểm biểu diễn của số phức w là đường tròn tâm I , với tâm I là điểm biểu diễn của số phức 2 -3i + 1 + i = 3 - 2i, tức là I(3; -2), bán kính r = 1.

Vậy

CHỌN BỘ SÁCH BẠN MUỐN XEM

100 câu trắc nghiệm Số phức nâng cao (có đáp án)

100 câu trắc nghiệm Số phức nâng cao-P1 (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương