Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) (Đề 1)
-
3041 lượt thi
-
50 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Nếu hoặc là TCN của đồ thị hàm số.
Cách giải:
Đồ thị hàm số có tiệm cận ngang là:Câu 2:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Sử dụng công thức tính đạo hàm của một tích
Cách giải:
Ta có:Câu 3:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Sử dụng công thức tính thể tích khối cầu.
Cách giải:
Công thức tính V của khối cầu có bán kính r:Câu 4:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng công thức tính thể tích chóp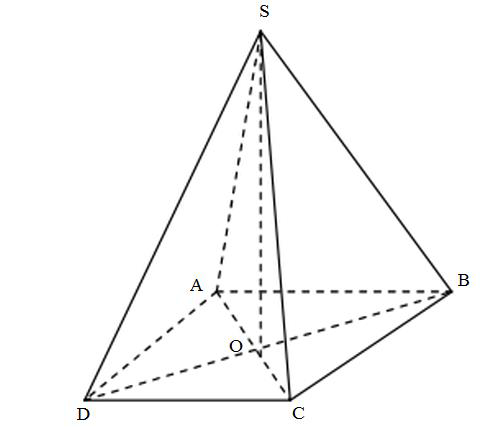
Gọi
Diện tích đáy:
ABCD là hình vuông tâm O
Tam giác SOB vuông tại O
Thể tích khối chóp:
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Hàm số xác định khi và chỉ khi
Cách giải:
ĐKXĐ:
TXĐ:Câu 6:
Cho hình chóp tam giác đều có cạnh bên là b và chiều cao là h (b > h). Tính thể tích của khối chóp đó.
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+) Gọi G là trọng tâm tam giác ABC
+) Tính diện tích tam giác đều ABC theo b và h.Cách giải:
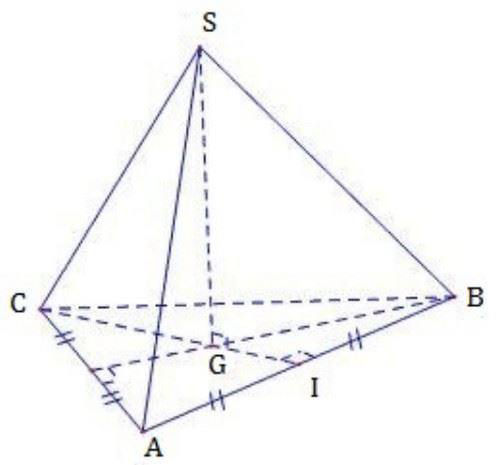
Gọi G là trọng tâm tam giác ABC
Tam giác SCG vuông tại GCâu 7:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
+) Xác định m để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.
+) Cô lập m, sử dụng phương pháp hàm số.
Cách giải:
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
+) : vô lý Phương trình (*) không có nghiệm với mọi m
+)
Xét hàm số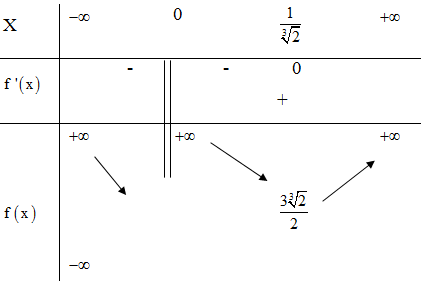
Số nghiệm của phương trình (**) là số giao điểm của đồ thị hàm số và đường thẳng song song với trục hoành.
Để phương trình ban đầu có 3 nghiệm phân biệt có 3 nghiệm phân biệt khác 0Câu 8:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Thể tích khối chóp
Cách giải:
Thể tích khối chóp ban đầu:
Theo đề bài, ta có:
Thể tích khối chóp đó giảm 3 lần.Câu 9:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số và đường thẳng
Cách giải:
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số và đường thẳng
Để (*) có 3 nghiệm thực phân biệt thìCâu 10:
 Xem đáp án
Xem đáp án
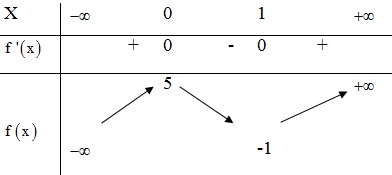
Đáp án D
Phương pháp:
Nếu đổi dấu khi qua điểm là điểm cực trị của hàm số.
Cách giải:
Tại đổi dấu từ âm sang dương Hàm số có điểm cực tiểu bằng 1.Câu 11:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Sử dụng công thức tính logarit của 1 tích.
Cách giải:
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án A
* Định nghĩa tiệm cận ngang của đồ thị hàm số
Nếu hoặc là TCN của đồ thị hàm số.
* Định nghĩa tiệm cận đứng của đồ thị hàm số
Nếu hoặc hoặc thì là TCĐ của đồ thị hàm số.
Cách giải:
TXĐ:
Đồ thị (C) có TCN là
Đồ thị (C) có TCĐ là
Đồ thị hàm số (C) có tất cả 4 đường tiệm cận.
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Thể tích khối hộp chữ nhật:
Cách giải:
Thể tích khối hộp chữ nhật ABCD.A’B’C’D’:Câu 14:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số tại điểm là:
Cách giải:Tiếp tuyến của (C) vuông góc với đường thẳng nên tiếp tuyến có hệ số góc
Gọi là tiếp điểm+) Phương trình tiếp tuyến:
Ta có:Câu 15:
 Xem đáp án
Xem đáp án
Đáp án D.
Phương pháp:+) Gọi
+)Cách giải:
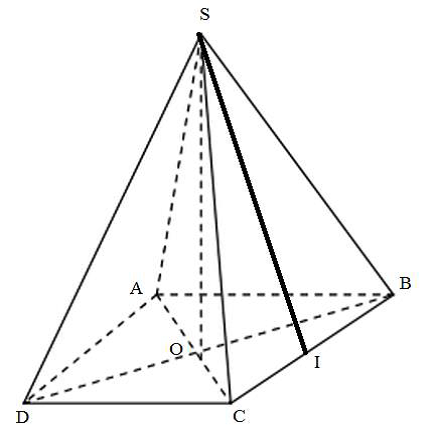
Gọi b là độ dài cạnh bên, I là trung điểm của BC
Tam giác SIB vuông tại I
Diện tích đáy:
Theo đề bài, ta có:
ABCD là hình vuông cạnh a
Gọi
Tam giác SOB vuông tại O
Thể tích của khối chópCâu 16:
 Xem đáp án
Xem đáp án
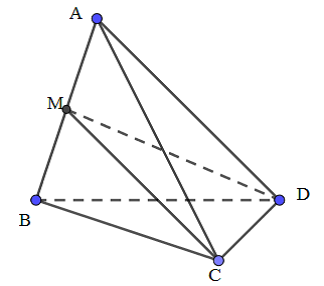
Cách giải:
Mặt phẳng (MCD) chia khối tứ diện ABCD thành hai khối đa diện là: A.MCD và M.BCDCâu 17:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Giải phương trình hoành độ giao điểm.
Cách giải:
Cho
Vậy đồ thị hàm số cắt trục hoành tại 3 điểmCâu 18:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Tính y’, xét dấu y’ và tìm các khoảng đơn điệu của hàm số.
Cách giải:
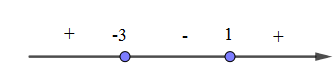
Hàm số nghịch biến trên khoảng (-3;1)
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng các công thức:
Cách giải:Câu 20:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số trên
Bước 1: Tính y’, giải phương trình
+) Bước 2: Tính các giá trị
+) Bước 3:
Cách giải:
Hàm số đã cho liên tục trên đoạn có
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Diện tích xung quanh của hình trụ:
Cách giải:
Diện tích xung quanh của hình trụ:Câu 22:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
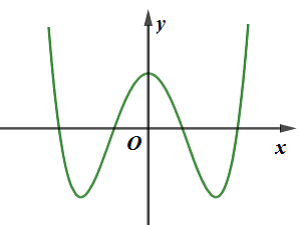
Nhận biết đồ thị hàm số bậc bốn trùng phương, hàm số bậc ba.
Cách giải:
Quan sát đồ thị hàm số, ta thấy: đây không phải đồ thị hàm số bậc 3 Loại bỏ phương án B và D
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương Chọn phương án CCâu 23:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp khối tứ diện là điểm cách đều tất cả các đỉnh của tứ diện.
+) Áp dụng định lí Pytago tính bán kính mặt cầu ngoại tiếp tứ diện.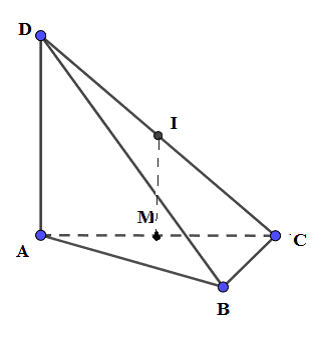
Tam giác ABC vuông tại B, M là trung điểm của AC M là tâm đường tròn ngoại tiếp tam giác ABC
Gọi I là trung điểm của CD
Ta có: IM là đường trung bình của tam giác ACD
Mà
Do đó, IM là trục đường tròn ngoại tiếp tam giác ABC
Từ (1), (2) I là tâm mặt cầu ngoại tiếp tứ diện ABCD, bán kính mặt cầu:Câu 24:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+) Xác định góc giữa SC và mặt đáy là góc giữa SC và hình chiếu của nó trên (ABCD).Cách giải:
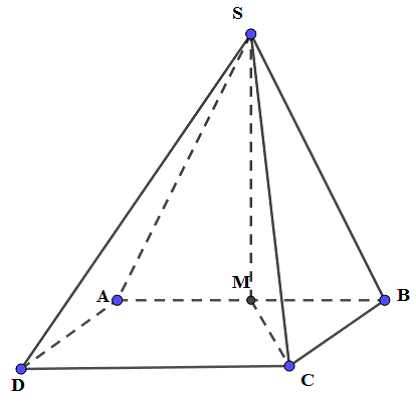
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Thể tích khối chóp vuông
Cách giải:
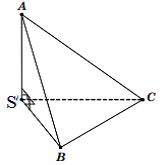
S.ABC có SA, SB, SC đôi một vuông góc với nhau
S.ABC là tứ diện vuông tại đỉnh SCâu 26:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Đặt ẩn phụ, đưa về phương trình bậc hai một ẩn. Giải phương trình và suy ra ẩn t.
Cách giải:Câu 27:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Thay tọa độ điểm M và các hàm số.
Cách giải:
Ta có: luôn đúng nằm trên đồ thị hàm sốCâu 28:
 Xem đáp án
Xem đáp án
Đáp án C
Cách giải:
Công thức diện tích xung quanh của hình nón:Câu 29:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số tại điểm làCâu 30:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Cho hàm sốVới
Với
VớiCách giải:
Vì Hàm số xác định
Vậy tập xác định D của hàm số làCâu 31:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng tính chất:
+) Hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
+) Hàm số chẵn nhận trục Oy làm trục đối xứng.
Cách giải:
+)
Ta có
Hàm số là hàm lẻ Đồ thị nhận điểm O làm tâm đối xứng A đúng
+) Cho Đồ thị hàm số cắt trục tung tại điểm duy nhất B đúng
+) Xét phương trình hoành độ giao điểm Đồ thị cắt trục hoành tại 3 điểm phân biệt D đúng.
Câu 33:
 Xem đáp án
Xem đáp án
Đáp án A
Cách giải:
Khẳng định sai là: Mỗi cạnh là cạnh chung của ít nhất ba mặt.Câu 34:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Xác định tỉ số chiều cao và tỉ số diện tích đáy của chóp I.ABCD và khối hộp ABCD.A’B’C’D’.
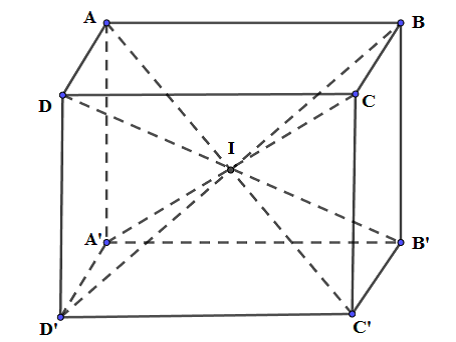
Câu 35:
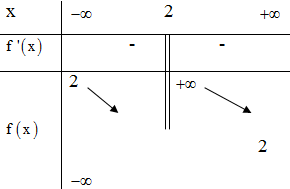
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Dựa vào TCĐ và TCN của đồ thị hàm số.
Cách giải:Câu 36:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Đưa phương trình về dạng tích sau đó giải phương trình logarit cơ bản.
Cách giải:ĐKXĐ:
Ta cóCâu 37:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số trên
Bước 1: Tính y’, giải phương trình
+) Bước 2: Tính các giá trị
+) Bước 3:
Cách giải:Câu 38:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Hàm số nghịch biến trên khi và chỉ khi tại hữu hạn điểm.
Cách giải:Câu 39:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số trên
Bước 1: Tính y’, giải phương trình
+) Bước 2: Tính các giá trị
+) Bước 3:
Cách giải:
Hàm số nghịch biến trênCâu 40:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Thể tích khối lăng trụ:
Cách giải: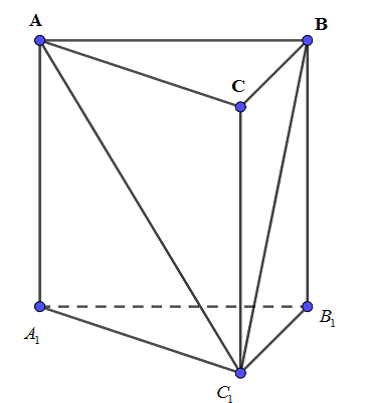
Câu 41:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Xét hàm số
+) : Hàm số đồng biến trên R.
+) : Hàm số nghịch biến trên R.
Cách giải:
Hàm số nào đồng biến trên R là:Câu 42:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Nếu là điểm cực đại của hàm số.
Ta có:
Điểm cực đại của đồ thị hàm số đã cho là:Câu 43:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng công thức đổi cơ số:Cách giải:
Ta cóCâu 45:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Nếu là điểm cực tiểu của hàm số.
Cách giải:
Câu 46:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Giải phương trình logarit cơ bản:
Cách giải:Câu 47:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Công thức lãi kép, không kỳ hạn:
Với: là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%).
Cách giải:
Số tiền ông A rút ra sau 5 năm đầu là: (triệu đồng)
Số tiền ông A tiếp tục gửi là: (triệu đồng)
Số tiền ông A nhận được sau 5 năm còn lại là: (triệu đồng)
Sau 10 năm ông A đã thu được số tiền lãi là: (triệu đồng)Câu 48:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp :
Nếu đổi dấu khi qua điểm là điểm cực trị của hàm số.
Cách giải:
đổi dấu từ - sang + tại Hàm số đạt cực tiểu tạiCâu 49:
 Xem đáp án
Xem đáp án
Đáp án A
* Định nghĩa tiệm cận ngang của đồ thị hàm số
Nếu hoặc là TCN của đồ thị hàm số.
* Định nghĩa tiệm cận đứng của đồ thị hàm số
Nếu hoặc hoặc thì là TCĐ của đồ thị hàm số.
Cách giải:
Hàm số có TCN là , TCĐ
Câu 50:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Xét từng hàm số, giải bất phương trình
Cách giải:
tại điểm duy nhất
Hàm số đồng biến trên khoảng