Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án (P1) (Vận dụng)
-
1349 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Điểm I(2;-3) là tâm đối xứng của những đồ thị hàm số nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án C
Đồ thị hàm số (1) có tâm đối xứng là nên loại.
Đồ thị hàm số (2) có tâm đối xứng là nên đúng.
Đồ thị hàm số (3) có tâm đối xứng là nên đúng
Đồ thị hàm số (4) có tâm đối xứng là nên loại.
Đồ thị hàm số (5) có tâm đối xứng là nên loại.
Câu 2:
Cho hàm số y = f(x) có bảng biến thiên:
Số nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Đáp án A
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng
Ta có BBT:
Dựa bào BBT ta thấy đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt.
Phương trình có 3 nghiệm phân biệt
Câu 4:
Cho hàm số f(x) liên tục trên và có bảng biến thiên dưới đây:
Số nghiệm của phương trình f(x) = 5 là:
 Xem đáp án
Xem đáp án
Đáp án A
Nghiệm của phương trình f(x) = 5 là số giao điểm của đường thẳng y = 5 và đồ thị hàm số
Dựa vào BBT ta thấy đường thẳng y = 5 > 3 cắt đồ thị hàm số tại 1 điểm
Vậy phương trình f(x) = 5 có duy nhất 1 nghiệm
Câu 5:
Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm cực tiểu của nó
 Xem đáp án
Xem đáp án
Đáp án B
Ta có: hoặc hoặc
Ta có bảng biến thiên:
Quan sát bảng biến thiên ta thấy tiếp điểm là và
Vậy phương trình đường tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là y = - 5
Câu 6:
Viết phương trình tiếp tuyến của đồ thị hàm số (C) tại điểm có hoành độ là nghiệm của phương trình y" = 0
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Với x = - 1 ta có:
Khi đó phương trình tiếp tuyến của đồ thị (C) tại điểm M là:
Câu 7:
Cho hàm số Kết luận nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án A
Ta có:
Suy ra hàm số luôn đồng biến trên mỗi khoảng
Do đó: giá trị lớn nhất trên đoạn là
Câu 8:
Cho hàm số . Đường thẳng d: y = x + m với m < 0 cắt đồ thị (C) tại hai điểm A, B phân biệt và khi m nhận giá trị nào trong các giá trị sau đây?
 Xem đáp án
Xem đáp án
Đáp án A

Với thì
![]()
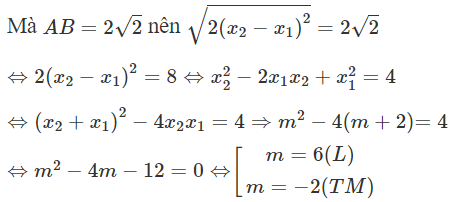
Câu 9:
Tiếp tuyến của đồ thị hàm số song song với đường thẳng có phương trình là:
 Xem đáp án
Xem đáp án
Đáp án A
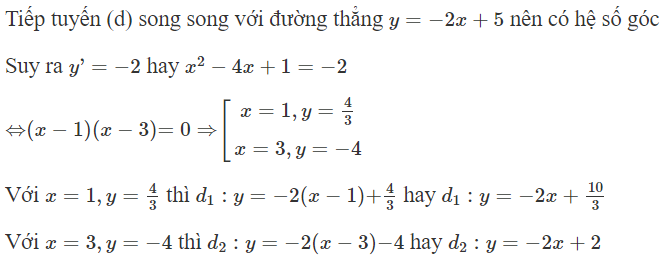
Câu 10:
Tìm giá trị của tham số m sao cho đồ thị của hàm số nhận điểm A(1; 3) làm tâm đối xứng
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Do A (1; 3) là điểm uốn
Câu 11:
Cho hàm số . Trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số nằm trên đường thẳng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án A
Ta có:
Với x = - 1 thì y = - 2. Vậy M (-1; - 2) là trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số.
Mà
Câu 13:
Biết đồ thị hàm số và đường thẳng cắt nhau tại hai điểm phân biệt và . Tính
 Xem đáp án
Xem đáp án
Đáp án D
Phương trình hoành độ giao điểm:
Ta có: mà là nghiệm phương trình (1) nên
Vậy
Câu 15:
Đồ thị hàm số có đường tiệm cận đi qua điểm A(-2; 7) khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án A
Đồ thị hàm số có đường tiệm cận
Đồ thị hàm số có đường tiệm cận đứng x = - 1 và tiệm cận ngang y = 2m + 1
Do đó đường tiệm cận đi qua điểm (thỏa mãn)
Câu 16:
Biết đồ thị hàm số có 2 điểm cực trị là: .Tính ?
 Xem đáp án
Xem đáp án
Đáp án B
có 2 nghiệm
Mà 2 điểm cực trị là (-1; 18) và (3; - 16) thuộc đồ thị nên ta có:
Giải hệ 4 phương trình ta có:
Câu 18:
Cho hàm số có đồ thị như hình vẽ. Xét hàm số . Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
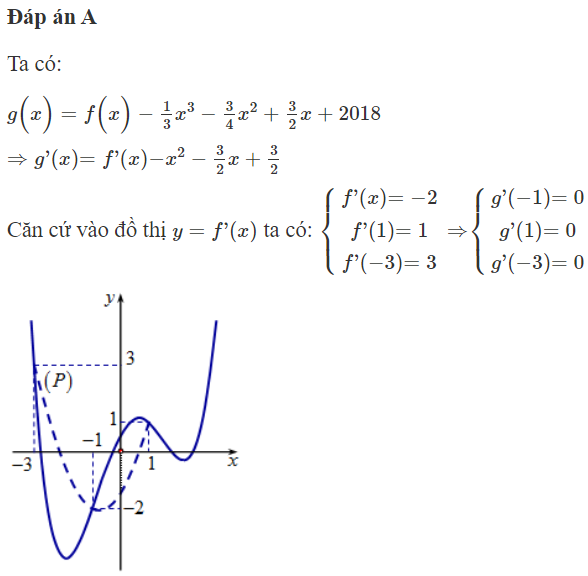
Ngoài ra, vẽ đồ thị (P) của hàm số trên cùng hệ trục tọa độ như hình vẽ bên (đường nét đứt)
ta thấy (P) đi qua các điểm với đỉnh . Rõ ràng:
- Trên khoảng (-1; 1) thì , nên
- Trên khoảng (-3; -1) thì , nên
Từ những nhận định trên, ta có bảng biến thiên của hàm số trên
Câu 20:
Hình vẽ bên là đồ thị hàm trùng phương. Giá trị của m để phương trình có 4 nghiệm đôi một khác nhau là:
 Xem đáp án
Xem đáp án
Đáp án C
Đồ thị là:
Phương trình có 4 nghiệm phân biệt

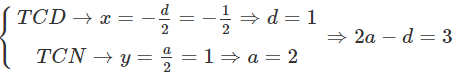
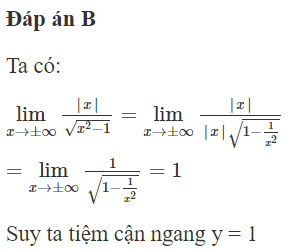
![Tìm tất cả các giá trị của m để hàm số f ( x ) = m x + 1 /x − m có giá trị lớn nhất trên [1; 2] bằng – 2 (ảnh 1)](https://hamchoi.vn/storage/uploads/images/3093/7-1642906123.png)