Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 21)
-
1510 lượt thi
-
71 câu hỏi
-
75 phút
Danh sách câu hỏi
Câu 1:
Tìm x:
x : 0,25 + x ´ 11 = 24
 Xem đáp án
Xem đáp án
x : 0,25 + x ´ 11 = 24
x ´ 4 + x ´ 11 = 24
x ´ (4 + 11) = 24
x ´ 15 = 24
x = 24 : 15
x = 1,6
Vậy x = 1,6.
Câu 2:
Tìm x:
x ´ 8,01 – x : 100 = 38
 Xem đáp án
Xem đáp án
x ´ 8,01 – x ´ 0,01 = 38
x ´ (8,01 – 0,01) = 38
x ´ 8 = 38
x = 38:8
x = 4,75
Vậy x = 4,75
Câu 3:
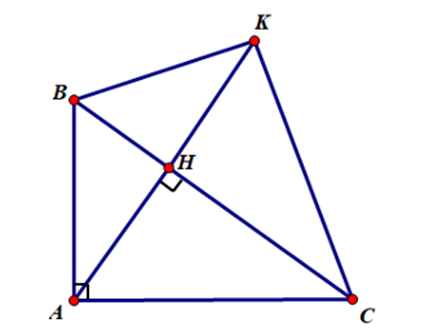
Cho tam giác ABC vuông tại A. Đường cao AH. Kẻ phân giác của cắt AH tại M, kẻ phân giác của cắt BH tại N. Chứng minh rằng MN // AB.
 Xem đáp án
Xem đáp án
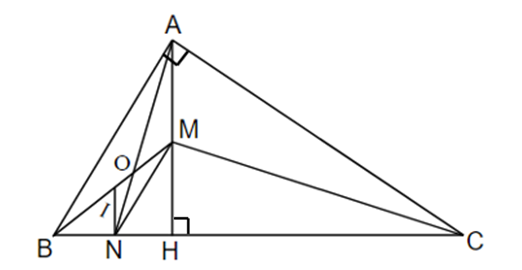
Áp dụng định lý đường phân giác trong tam giác ta có:
Xét ΔAHB và ΔCHA có:
AH chung
(cùng phụ với )
Do đó ΔAHB ᔕ ΔCHA (g.g)
Suy ra
Do đó,
Suy ra MN // AB (định lý Ta-let đảo)
Vậy MN // AB.
Câu 4:
Tìm x:
x × 9,8 – x : 0,25 = 18,096
 Xem đáp án
Xem đáp án
x × 9,8 – x : 0,25 = 18,096
x × 9,8 – x × 4 = 18,096
x × (9,8 – 4) = 18,096
x × 4,8 = 18,096
x = 18,096 : 4,8
x = 3,77
Câu 5:
Tìm x:
0,16 : (x : 3,5) = 2,8
 Xem đáp án
Xem đáp án
0,16 : (x : 3,5) = 2,8
0,16 : x × 3,5 = 2,8
0,56 : x = 2,8
x = 0,56 : 2,8
x = 0,2
Vậy x = 0,2
Câu 6:
Giải phương trình: x4 + 2x2 – 3 = 0
 Xem đáp án
Xem đáp án
x4 + 2x2 – 3 = 0
⇔ (x4 + 2x2 + 1) – 4 = 0
⇔ (x2 + 1)2 − 22 = 0
⇔ (x2 + 1 − 2)(x2 + 1 + 2) = 0
⇔ (x2 – 1)(x2 + 3) = 0
Vì x2 ≥ 0 nên x2 + 3 > 0 với mọi x
Do đó x2 – 1 = 0
⇔ x2 = 1
⇔ x = ± 1
Vậy tập nghiệm của phương trình đã cho là S = {−1; 1}.
Câu 7:
Giải phương trình: x4 – 4x3 – 2x2 + 12x + 5 = 0.
 Xem đáp án
Xem đáp án
x4 – 4x3 – 2x2 + 12x + 5 = 0
⇔ (x4 – 4x3 + 4x2)– 6x2 + 12x + 5 = 0
⇔ (x2 – 2x)2 – 6(x2 – 2x) + 5 = 0
⇔ (x2 – 2x)2 – (x2 – 2x) – 5(x2 – 2x) + 5 = 0
⇔ (x2 – 2x)(x2 – 2x – 1) – 5(x2 – 2x – 1) = 0
⇔ (x2 – 2x – 1)(x2 – 2x – 5) = 0
Vậy tập nghiệm của phương trình đã cho là .
Câu 8:
Phân tích đa thức thành nhân tử: x3 – x2y – xy2 + y3.
 Xem đáp án
Xem đáp án
Ta có: x3 – x2y – xy2 + y3
= x2(x – y) – y2(x – y)
= (x2 – y2)(x – y)
= (x – y)2(x + y)
Câu 9:
Phân tích đa thức thành nhân tử: –6x2 – 9xy + 15y2.
 Xem đáp án
Xem đáp án
–6x2 – 9xy + 15y2
= –(6x2 + 9xy – 15y2)
= –(6x2 – 6xy + 15xy – 15y2)
= –[6x(x – y) + 15y(x – y)]
= –[(x – y)(6x + 15y)]
Câu 10:
Cho a là góc tù và . Tính giá trị của biểu thức: A = 2sin a – cos a.
 Xem đáp án
Xem đáp án
Ta có: sin2 α + cos2 α = 1
⇒ cos2 α = 1 − sin2 α
Mà α là góc tù ⇒ cos α < 0
Vậy
Câu 11:
Cùng một lúc hai xe xuất phát từ hai địa điểm A và B cách nhau 80 km. Chúng chuyển động thẳng đều và cùng chiều từ A đến B. Xe thứ nhất khởi hành từ A với vận tốc 30 km/h. Xe thứ hai đi từ B với vận tốc 40 km/h. Tính khoảng cách giữa hai xe sau 1 giờ kể từ lúc xuất phát.
 Xem đáp án
Xem đáp án
Sau 1 giờ, xe thứ nhất đi được quãng đường là:
30. 1 = 30 (km)
Sau 1 giờ, xe thứ hai đi được quãng đường là:
40. 1 = 40 (km)
Sau 1 giờ, hai xe cách nhau quãng đường là:
80 – 30 – 40 = 10 (km)
Đáp số: 10 km
Câu 12:
Cùng một lúc hai xe xuất phát từ hai địa điểm A và B cách nhau 160 km. Chúng chuyển động thẳng đều và cùng chiều từ A đến B. Xe thứ nhất khởi hành từ A với vận tốc 30 km/h. Xe thứ hai đi từ B với vận tốc 40 km/h. Sau khi xuất phát 1 giờ, xe thứ nhất tăng tốc và đạt tối đa vận tốc 50 km/h. Xác định thời điểm hai xe gặp nhau.
 Xem đáp án
Xem đáp án
Sau 1 giờ, xe thứ nhất đi được quãng đường là:
30. 1 = 30 (km)
Sau 1 giờ, xe thứ hai đi được quãng đường là:
40. 1 = 40 (km)
Sau 1 giờ, hai xe cách nhau quãng đường là:
160 – 30 – 40 = 90 (km)
Sau khi xe thứ nhất tăng tốc, thời gian hai xe gặp nhau là:
90 : (50 + 40) = 1 (giờ)
Tổng thời gian 2 xe đã đi là:
1 + 1 = 2 (giờ)
Đáp số: 2 giờ.
Câu 13:
Tìm m, n nguyên dương thỏa mãn: .
 Xem đáp án
Xem đáp án
Ta có:
Û 7m + 7n – mn = 0
Û m(7 – n) + 7n – 49 = –49
Û m(7 – n) – 7(7 – n) = –49
Û (m – 7)(7 – n) = –49
Lập bảng xét các trường hợp:
|
7 – n |
1 |
–1 |
49 |
–49 |
7 |
–7 |
|
m – 7 |
–49 |
49 |
–1 |
1 |
–7 |
7 |
|
n |
6 |
8 |
–42 |
56 |
0 |
14 |
|
m |
–42 (loại) |
56 (TM) |
6 (loại) |
8 (TM) |
0 (loại) |
14 (TM) |
Vậy các cặp nguyên dương (m; n) thoả mãn là: (56; 8); (8; 56); (14; 14).
Câu 14:
Tìm m, n nguyên thỏa mãn: .
 Xem đáp án
Xem đáp án
Ta có:
Û 3m + 3n – mn = 0
Û m(3 – n) + 3n – 9 = –9
Û m(3 – n) – 3(3 – n) = –9
Û (m – 3)(3 – n) = –9
Lập bảng xét các trường hợp:
|
3 – n |
1 |
– 1 |
9 |
– 9 |
3 |
– 3 |
|
m – 3 |
– 9 |
9 |
– 1 |
1 |
– 3 |
3 |
|
n |
2 |
4 |
– 6 |
12 |
0 |
6 |
|
m |
– 6 (TM) |
12 (TM) |
2 (TM) |
4 (TM) |
0 (TM) |
6 (TM) |
Vậy các cặp nguyên dương (m; n) thoả mãn là: (2; –6 ); (4; 12); (–6; 2); (12; 4); (0; 0); (6; 6)
Câu 15:
Đĩa xích của xe đạp có 80 răng, đĩa líp có 40 răng. Tính số truyền i và cho biết chi tiết nào quay nhanh hơn?
 Xem đáp án
Xem đáp án
Áp dụng công thức ta có:
Vậy tỉ số truyền ở đây là: .
Vậy chi tiết đĩa líp quay nhanh hơn đĩa xích 4 lần.
Câu 16:
 Xem đáp án
Xem đáp án
Vậy tập nghiệm của phương trình đã cho là S = {– 2; 0,2}.
Câu 17:
 Xem đáp án
Xem đáp án
Các thừa số tròn chục trong tích trên là: 10; 20; 30 và 40
Þ Các thừa số trên tạo ra 4 chữ số 0.
Các thừa số có tận cùng là chữ số 5 trong tích trên là: 5; 15; 25; 35 và 45
trong đó, 25 = 5 × 5.
Mỗi thừa số có tận cùng là chữ số 5 nhân với một thừa số chẵn sẽ tạo ra một số có tận cùng là chữ số 0.
Do đó các thừa số trên tạo ra 6 chữ số 0.
Tích 1 × 2 × 3 × 4 × 5 × … × 45 × 46 có tận cùng số chữ số 0 là:
4 + 6 = 10 (chữ số)
Vậy tích 1 × 2 × 3 × 4 × 5 × … × 45 × 46 có tận cùng 10 chữ số 0.
Câu 18:
Tích 2 × 11 × 6 × 14 × 15 × 17 × 18 × 25 × 45 có tận cùng bao nhiêu chữ số 0?
 Xem đáp án
Xem đáp án
Các thừa số có tận cùng là chữ số 5 trong tích trên là: 15; 25 và 45
trong đó, 25 = 5 × 5.
Mỗi thừa số có tận cùng là chữ số 5 nhân với một thừa số chẵn sẽ tạo ra một số có tận cùng là chữ số 0.
Do đó các thừa số trên tạo ra 4 chữ số 0
Vậy 2 × 11 × 6 × 14 × 15 × 17 × 18 × 25 × 45 có tận 4 chữ số 0.
Câu 19:
Xác định hàm số y = ax2 + bx + c có giá trị nhỏ nhất bằng khi và nhận giá trị bằng 1 khi x = 1.
 Xem đáp án
Xem đáp án
Hàm số y = ax2 + bx + c có giá trị nhỏ nhất bằng khi nên ta có:
(1)
(2)
Hàm số y = ax2 + bx + c nhận giá trị bằng 1 khi x = 1 nên ta có:
a + b + c = 1 (3)
Từ (1), (2) và (3) ta có:
Vậy hàm số cần tìm là: y = x2 – x + 1.
Câu 20:
Xác định hàm số y = ax2 + bx + c có giá trị nhỏ nhất bằng 2 khi x = 1 và nhận giá trị bằng 3 khi x = 2.
 Xem đáp án
Xem đáp án
Hàm số y = ax2 + bx + c có giá trị nhỏ nhất bằng 2 khi x = 1 nên ta có:
(1)
2 = a. 12 + b. 1 + c Û a + b + c = 2 (2)
Hàm số y = ax2 + bx + c nhận giá trị bằng 3 khi x = 2 nên ta có:
4a + 2b + c = 3 (3)
Từ (1), (2) và (3) ta có:
Vậy hàm số cần tìm là: y = x2 – 2x + 3.
Câu 21:
Cho đa thức p(x) = ax2 + bx + c (với a, b, c là các số hữu tỉ). Biết P(0), P(1), P(2) là các số nguyên. Chứng minh P(x) có giá trị nguyên với mọi x nguyên.
 Xem đáp án
Xem đáp án
Lời giải
P(0) = c mà P(0) nguyên
Þ c nguyên
P(1) = a + b + c mà P(1) nguyên
Þ a + b + c nguyên mà c nguyên
Þ a + b nguyên
P(2) = 4a + 2b + c mà P(2) nguyên
Þ 4a + 2b + c nguyên mà c nguyên
Þ 4a + 2b nguyên hay 2a + b nguyên
Þ 2a + b − (a + b) nguyên
Þ a nguyên mà a + b nguyên
Þ b nguyên
Do đó a, b, c nguyên
Vậy P(x) có giá trị nguyên với mọi x nguyên.
Câu 22:
Cho tam giác ABC có A’, B’, C’ lần lượt là trung điềm của các cạnh BC, CA, AB. Chứng minh .
 Xem đáp án
Xem đáp án
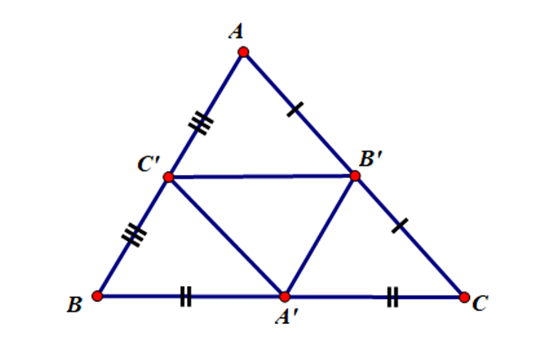
Tam giác ABC có A’B’, B’C’, C’A’ là các đường trung bình của tam giác
Ta có:
(đpcm)
Vậy .
Câu 23:
Cho tam giác ABC, M điểm bất kì, G là trọng tâm. Chứng minh MA2 + MB2 + MC2 = 3MG2 + GA2 + GB2 + GC2.
 Xem đáp án
Xem đáp án
G là trọng tâm tam giác ABC nên
Ta có: MA2 + MB2 + MC2 =
(đpcm)
Vậy MA2 + MB2 + MC2 = 3MG2 + GA2 + GB2 + GC2.
Câu 24:
Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB. Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.
 Xem đáp án
Xem đáp án
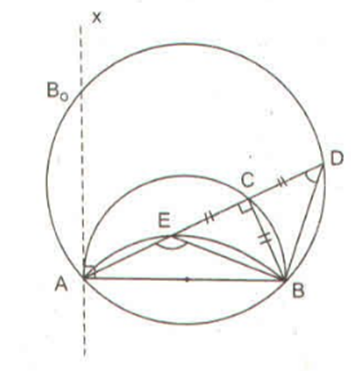
Ta có: AB cố định
(vì tam giác BCD vuông cân)
Suy ra khi C chuyển động trên nửa đường tròn đường kính AB cố định thì D chuyển động trên cung chứa góc 45° dựng trên đoạn thẳng AB cố định.
Gọi B0 là giao điểm của tiếp tuyến Ax với cung chứa góc 45° dựng trên đoạn thẳng AB cố định.
Dây AC thay đổi phụ thuộc vị trí điểm C trên nửa đường tròn đường kính AB cố định.
AC lớn nhất khi AC = AB Û
Khi đó,
AC nhỏ nhất khi AC = 0 Û
Khi đó,
Vậy quỹ tích các điểm D khi C chạy trên nửa đường tròn đường kính AB là cung BB0 nằm trên cung chứa góc 45° dựng trên đoạn thẳng AB cố định, trong nửa mặt phẳng bờ AB có chứa điểm C (bị giới hạn bởi tiếp tuyến).
Câu 25:
Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB. Trên tia CA lấy điểm E sao cho CE = CB. Tìm quỹ tích các điểm E khi C chạy trên nửa đường tròn đã cho.
 Xem đáp án
Xem đáp án
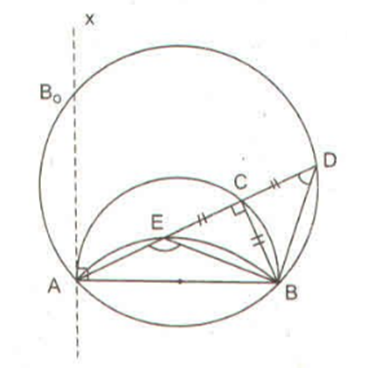
Ta có: AB cố định
(góc ngoài của tam giác BCE vuông cân)
Suy ra khi C chuyển động trên nửa đường tròn đường kính AB cố định thì E chuyển động trên cung chứa góc 135° dựng trên đoạn thẳng AB cố định.
Vậy quỹ tích các điểm E khi C chạy trên nửa đường tròn đường kính AB là cung chứa góc 135° dựng trên đoạn thẳng AB cố định.
Câu 26:
Có 6 quả cầu xanh đánh số từ 1 đến 6, 5 quả cầu đỏ đánh số từ 1 đến 5 và 7 quả màu vàng đánh số từ 1 đến 7. Hỏi có bao nhiêu cách lấy ra 3 quả cầu vừa khác màu vừa khác số?
 Xem đáp án
Xem đáp án
Để lấy ra ba quả cầu vừa khác màu vừa khác số ta phải thực hiện qua ba giai đoạn:
+ Chọn một quả cầu đỏ
+ Chọn một quả cầu xanh
+ Chọn một quả cầu vàng
Chọn quả cầu đỏ có 5 cách chọn
Chọn quả cầu xanh có 5 cách chọn (trừ quả cầu được đánh số trùng với quả cầu đỏ)
Chọn quả cầu vàng có 5 cách chọn (trừ hai quả cầu được đánh số trùng với quả cầu đỏ và quả cầu xanh)
Theo quy tắc nhân ta được 5. 5. 5 = 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số
Vậy có 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số.
Câu 27:
Một hộp đựng 15 viên bi khác nhau gồm 4 bi đỏ, 5 bi trắng và 6 bi vàng. Tính số cách chọn 4 viên bi từ hộp đó sao cho không có đủ 3 màu.
 Xem đáp án
Xem đáp án
Trường hợp 1: chọn 4 bi đỏ hoặc trắng có: (cách)
Trường hợp 2: chọn 4 bi đỏ và vàng hoặc 4 bi vàng có (cách)
Trường hợp 3: chọn 4 bi trắng và vàng có (cách)
Số cách chọn 4 viên bi từ hộp đó sao cho không có đủ 3 màu là:
126 + 209 + 310 = 645 (cách)
Vậy có 645 cách.
Câu 28:
Cho tam giác ABC, . Kẻ đường cao AH. Trên tia đối của tia HA lấy điểm K sao cho HK = HA. Chứng minh ΔABH = ΔKBH.
 Xem đáp án
Xem đáp án
Xét ΔABH và ΔKBH có:
AH = KH (gt)
BH cạnh chung
Do đó ΔABH = ΔKBH (c.g.c)
Câu 29:
Cho các hàm số: y = 2x − 2 và y = (m + 1)x −𝑚2 – 𝑚 (m ≠ −1). Tìm m để đồ thị hai hàm số trên là các đường thẳng song song.
 Xem đáp án
Xem đáp án
Để hai đồ thị hàm số trên song song thì:
(vô lý)
Vậy không tồn tại m để 2 đường thẳng trên song song.
Câu 30:
Tìm m để hai đường thẳng (d): y = 3x + 1 và (d′): y = (m−1)x − 2m song song với nhau.
 Xem đáp án
Xem đáp án
Để d // d’ thì:
Vậy m = 4 thì d // d’.
Câu 31:
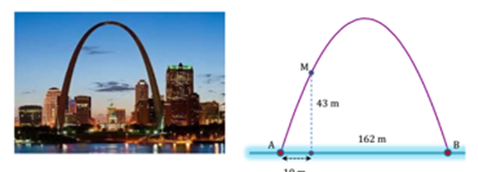
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng).
 Xem đáp án
Xem đáp án
Chọn hệ trục tọa độ Oxy như hình vẽ.
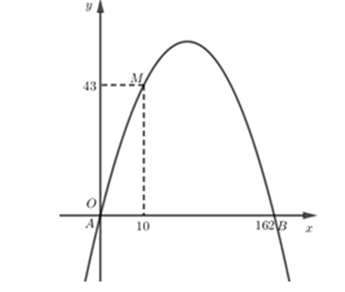
Phương trình Parabol (P) có dạng y = ax2 + bx + c
(P) đi qua điểm A(0; 0), B(162; 0) và M(10; 43) nên ta có:
Do đó chiều cao của cổng là:
Vậy độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng) khoảng 185,6 m.
Câu 33:
Cho phương trình: x2 – 2(m – 1)x + m2 – 3m + 4 = 0. Tìm hệ thức giữa x1 và x2 độc lập với m.
 Xem đáp án
Xem đáp án
Giả sử phương trình có hai nghiệm x1 và x2.
Theo Vi-et ta có:
Vậy hệ thức liên hệ giữa x1 và x2 độc lập với m là .
Câu 34:
Cho phương trình: x2 – 2(m – 1)x + m2 – 3m = 0. Tìm hệ thức giữa x1 và x2 độc lập với m.
 Xem đáp án
Xem đáp án
Giả sử phương trình có hai nghiệm x1 và x2.
Theo Vi-et ta có:
Câu 36:
Cho nửa đường tròn tâm O đường kính AB, tiếp tuyến Ax. Gọi C là một điểm trên nửa đường tròn. Tia phân giác của cắt nửa đường tròn tại E, AE và BC cắt nhau tại K. Chứng minh: ΔABK cân tại B.
 Xem đáp án
Xem đáp án
AE là phân giác của
Mà (góc nội tiếp và góc tạo bởi tiếp tuyến cùng chắn cung )
(1)
Ta có: (vì là góc nội tiếp chắn nửa đường tròn) (2)
Từ (1) và (2) ta có: (vì cùng phụ với hai góc bằng nhau)
Vậy ΔABK cân tại B.
Câu 37:
Cho ΔABC có trọng tâm G. Gọi H là điểm đối xứng của B qua G. Chứng minh .
 Xem đáp án
Xem đáp án
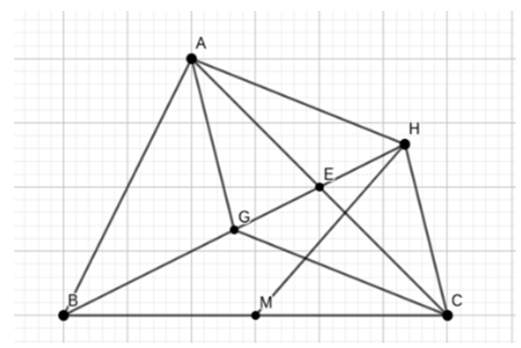
Ta có:
Vậy .
Câu 38:
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Chứng minh MN // (SCD).
 Xem đáp án
Xem đáp án
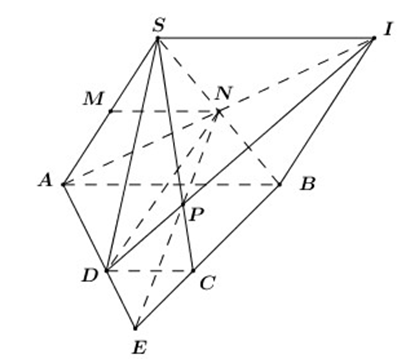
Ta có: MN là đường trung bình của ΔSAB
Þ MN // AB
Mà AB // CD (vì ABCD là hình thang)
Þ MN // CD
Lại có: CD Ì (SCD)
Þ MN // (SCD)
Vậy MN // (SCD).
Câu 39:
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Tìm P là giao điểm của SC và (ADN).
 Xem đáp án
Xem đáp án
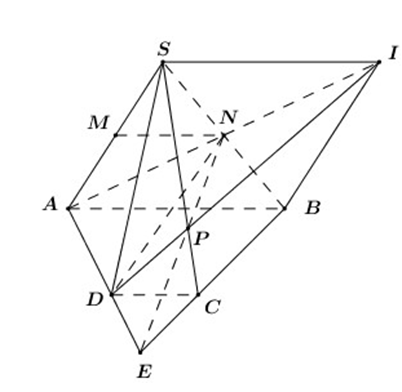
Trong (ABCD) gọi AD Ç BC = {E}
Ta có:
• E Î AD Ì (ADN) Þ E Î (ADN)
• E Î BC Ì (SBC) Þ E Î (SBC)
Do đó E Î (ADN) Ç (SBC)
Þ (ADN) Ç (SBC) = EN
Gọi SC Ç EN = {P}
Ta có: P Î SC
P Î EN Ì (ADN)
Þ P = SC Ç (ADN)
Vậy điểm P cần tìm là giao điểm của SC và ENCâu 40:
Hình thoi ABCD có diện tích 20 cm2 và đường chéo AC bằng 10 cm. Tính độ dài đường chéo BD.
 Xem đáp án
Xem đáp án
Độ dài đường chéo BD là:
Đáp số: 4 cm.
Câu 41:
Hình thoi ABCD có độ dài đường chéo AC là 20 cm. Độ dài đường chéo .Tính diện tích hình thoi ABCD.
 Xem đáp án
Xem đáp án
Độ dài đường chéo BD là:
Diện tích hình thoi ABCD là:
Đáp số: 120 cm2
Câu 42:
Cho đường tròn (O;R), đường kính AB. Vẽ dây cung BC = R. Tính các cạch và các góc chưa biết của tam giác ABC theo R.
 Xem đáp án
Xem đáp án
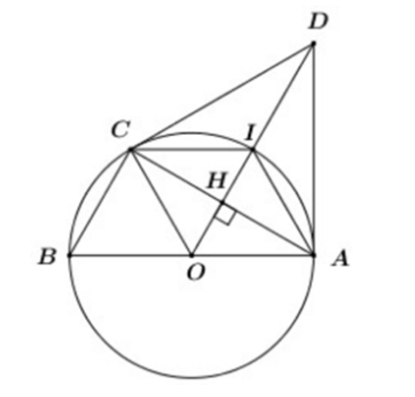
(góc nội tiếp chắn nửa đường tròn)
Áp dụng định lí Py-ta-go trong tam giác vuông ABC, ta có:
AB2 = AC2 + BC2
Û (2R)2 = AC2 + R2
Û AC2 = 3R2
Ta có:
Vậy ; ; .
Câu 43:
Cho đường tròn (O; R), đường kính AB. Vẽ dây cung BC = R. Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn (O) tại D. Chứng minh DC là tiếp tuyến của đường tròn (O).
 Xem đáp án
Xem đáp án
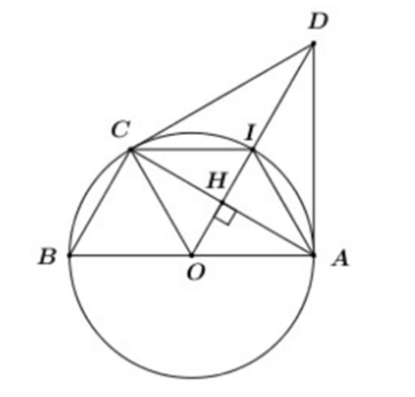
Gọi H = OD ∩ AC
Ta có: OD ⊥ AC tại H
⇒ H là trung điểm của AC
⇒ OD là trung trực của AC
⇒ DA = DC (tính chất đường trung trực).
Xét ΔOAD và ΔOCD có:
OA = OC (= R)
OD chung
DA = DC
Þ ΔOAD = ΔOCD (c.c.c)
Mà
Þ OC ⊥ CD
Vậy CD là tiếp tuyến của đường tròn (O) tại C.
Câu 44:
 Xem đáp án
Xem đáp án
Ta có: A = |x – 3| + |x – 5| + |x – 7|
= |x – 3| + |x – 5| + |7 – x| ≥ | x − 3 + 7 − x | + | x − 5 |
= | 4 | + | x − 5 |
= 4 + | x − 5 |
Do |x – 5| ≥ 0 nên 4 + |x – 5| ≥ 4
Þ |x – 3| + |x – 5| + |7 – x| ≥ 4
Dấu "=" xảy ra khi |x – 5| = 0
⇔ x − 5 = 0
⇔ x = 5
Vậy GTNN của A = 4 khi x = 5.
Câu 45:
 Xem đáp án
Xem đáp án
Ta có: M = |x + 5| + |x + 2| + |x – 7| + |x – 8|
³ |−x + 8 – x – 2 + x + 5 + x + 7| = 18
Dấu bằng xảy ra khi −5 £ x £ −2.
Vậy M có giá trị nhỏ nhất là 18 khi −5 £ x £ −2.
Câu 46:
Tìm n ∈ ℤ, biết:
(n – 3) + (n – 2) + (n – 1) + … + 10 + 11 = 11.
 Xem đáp án
Xem đáp án
(n – 3) + (n – 2) + (n – 1) + … + 10 + 11 = 11
Û (n – 3) + (n – 2) + (n – 1) + … + 10 = 0
Gọi số các số hạng từ n – 3 đến 10 là x (số hạng) ()
Ta có:
[10 + (n – 3)]. x : 2 = 0
Û (n + 7). x = 0
Vì x > 0 nên n + 7 = 0 Û n = –7 (tmđk)
Vậy n = –7.
Câu 47:
Tìm n ∈ ℤ, biết:
(n + 1) + (n + 2) + (n + 3) + (n + 4) = 90
 Xem đáp án
Xem đáp án
(n + 1) + (n + 2) + (n + 3) + (n + 4) = 90
Û 4n + 10 = 90
Û 4n = 80
Û n = 20
Vậy n = 20.
Câu 49:
Giải phương trình: |2x – 1| = 2x – 1.
 Xem đáp án
Xem đáp án
|2x – 1| = x + 2
• Với , ta có |2x – 1| = 2x – 1
Û 2x – 1 = x + 2
Û x = 3 (TMĐK)
• Với , ta có |2x – 1| = 1 – 2x
Û 1 – 2x = x + 2
Û 3x = –1
(TMĐK)
Vậy tập nghiệm của phương trình đã cho là .
Câu 50:
 Xem đáp án
Xem đáp án
(x + 3) – |x + 7| = 0
Û x + 3 = |x + 7|
• Với x ≥ –3, ta có: x + 3 = x + 7
Û 0 = 4 (vô lí)
• Với x < –3, ta có: x + 3 = –x – 7
Û 2x = –10
Û x = –5 (TMĐK)
Vậy nghiệm của phương trình đã cho là x = –5.
Câu 51:
Tìm x, y ∈ ℕ sao cho: xy + x + y = 17.
 Xem đáp án
Xem đáp án
xy + x + y = 17
Û x(y + 1) + (y + 1) = 18
Û (x + 1)(y + 1) = 18
Do x, y ∈ ℕ nên ta có bảng:
|
x + 1 |
1 |
2 |
3 |
6 |
9 |
18 |
|
y + 1 |
18 |
9 |
6 |
3 |
2 |
1 |
|
x |
0 |
1 |
2 |
5 |
8 |
17 |
|
y |
17 |
8 |
5 |
2 |
1 |
0 |
Vậy các cặp số (x, y) là (0; 17), (1; 8), (2; 5), (5; 2), (8; 1), (17; 0).
Câu 52:
Tìm tất cả các số nguyên dương n để n2 + 31 là số chính phương.
 Xem đáp án
Xem đáp án
Đặt n2 + 31 = a2 (a ∈ ℕ)
Û a2 – n2 = 33
Û (a - n)(a + n) = 33 = 1. 31
Dễ thấy a – n < a + n nên ta có:
Vậy n = 15
Câu 53:
Chứng minh rằng với mọi số nguyên x, y thì:
A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y4 là số chính phương.
 Xem đáp án
Xem đáp án
Ta có: A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y4
= (x2 + 5xy + 4y2)( x2 + 5xy + 6y2) + y4
Đặt x2 + 5xy + 5y2 = t (t ∈ ℕ)
A = (t – y2)(t + y2) + y4 = t2 – y4 + y4 = t2
Vậy A là số chính phương.
Câu 54:
Chứng minh A = n(n + 1)(n + 2)(n + 3) + 1 là số chính phương với n là số tự nhiên.
 Xem đáp án
Xem đáp án
Ta có: A = n(n + 1)(n + 2)(n + 3) + 1 = (n2 + 3n)(n2 + 3n + 2) + 1
Đặt n2 + 3n = t (t ∈ ℕ)
A = t(t + 2) + 1
= t2 + 2t + 1 = (t + 1)2
Vậy A là số chính phương.
Câu 55:
Tìm số dư của phép chia 37,99 cho 16 nếu lấy đến 2 chữ số ở phần thập phân của thương.
 Xem đáp án
Xem đáp án
Ta có: 37,99 = 16 × 2,37 + 0,07
Vậy số dư của phép chia 37,99 cho 16 là 0,07.
Câu 56:
Tìm số dư của phép chia 32,451 chia cho 24 nếu lấy đến 3 chữ số ở phần thập phân của thương.
 Xem đáp án
Xem đáp án
Ta có: 32,451 = 24 × 1,352 + 0,003
Vậy số dư của phép chia 32,451 chia cho 24 là 0,003.
Câu 57:
 Xem đáp án
Xem đáp án
Đặt n2 + 2n + 12 = k2
Û n2 + 2n + 1 + 11 = k2
Û (n + 1)2 + 11 = k2
Û k2 – (n + 1)2 = 11
Û (k – n – 1)(k + n + 1) = 11 = 1. 11
Dễ thấy k + n + 1 > k – n – 1 nên ta có:
Vậy n = 4.
Câu 58:
Tìm số tự nhiên n sao cho n2 + 3n là số chính phương.
 Xem đáp án
Xem đáp án
Đặt n2 + 3n = k2
Û 4n2 + 12n + 9 – 9 = 4k2
Û (2n + 3)2 – 4k2 = 9
Û (2n + 3 – 2k)(2n + 3 + 2k) = 9
Dễ thấy 2n + 3 + 2k > 2n + 3 – 2k nên ta có:
Vậy n = 1.
Câu 59:
 Xem đáp án
Xem đáp án
46 – (x – 11) = –48
Û x – 11 = 46 + 8
Û x – 11 = 94
Û x = 94 + 11
Û x = 105
Vậy nghiệm của phương trình đã cho là x = 105.
Câu 60:
Giải phương trình: 4x – 20 = 4
 Xem đáp án
Xem đáp án
4x – 20 = 4
Û 4x = 20 + 4
Û 4x = 24
Û x = 6
Vậy nghiệm của phương trình đã cho là x = 6.
Câu 61:
Giải phương trình:
7x3 + 12x2 – 4x = 0
 Xem đáp án
Xem đáp án
7x3 + 12x2 – 4x = 0
Û x(7x2 + 12x – 4) = 0
Û x(7x2 + 14x – 2x – 4) = 0
Û x[7x(x + 2) – 2(x + 2)] = 0
Û x(x + 2)(7x – 2) = 0
Vậy tập nghiệm của phương trình đã cho là .
Câu 62:
Giải phương trình:
x(x − 3) + 5x = x2 − 8
 Xem đáp án
Xem đáp án
x(x − 3) + 5x = x2−8
Û x(x − 3) + 5x − x2 + 8 = 0
Û x2 − 3x + 5x − x2 + 8 = 0
Û 2x + 8 = 0
Û 2x = −8
Û x = −4
Vậy nghiệm của phương trình đã cho là x = −4.
Câu 63:
Tìm m để hàm số xác định trên khoảng (−∞; −2).
 Xem đáp án
Xem đáp án
Tập xác định của hàm số là tập hợp các giá trị của x thỏa mãn điều kiện:
Để hàm số xác định trên khoảng (−∞;−2) cần có:
Þ m Î [−2; 3]
Vậy m Î [−2; 3].
Câu 64:
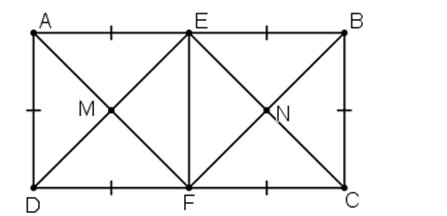
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tứ giác ADFE là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
E, F là trung điểm AB, CD
Ta có: AB = CD hay 2AD = 2BC
Þ AE = EB = BC = CF = FD = DA.
Tứ giác ADFE có AE // DF, AE = DF
Þ ADFE là hình bình hành.
Hình bình hành ADFE có
Þ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE = AD
Þ ADFE là hình vuông
Vậy ADFE là hình vuông.
Câu 65:
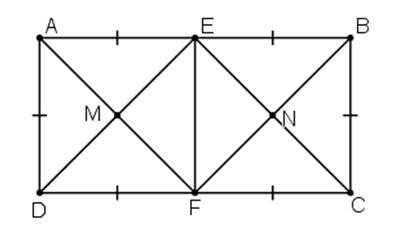
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tứ giác EMFN là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
E, F là trung điểm AB, CD
Ta có: AB = CD hay 2AD = 2BC
Þ AE = EB = BC = CF = FD = DA.
Tứ giác ADFE có AE // DF, AE = DF
Þ ADFE là hình bình hành.
Hình bình hành ADFE có
Þ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE = AD
Þ ADFE là hình vuông
Þ ME = MF, ME ⊥ MF.
Hình bình hành EMFN có nên EMFN là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.
Vậy EMFN là hình vuông.
Câu 66:
 Xem đáp án
Xem đáp án
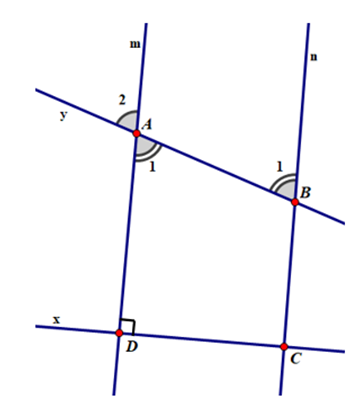
Vì (quan hệ từ vuông góc đến song song)
Vậy x ^ n.
Câu 67:
Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C khác A, B) vẽ tiếp tuyến CM cắt Ax tại M, hạ CH vuông góc với AB, MB cắt (O) tại Q và cắt CH tại N. Chứng minh MA2 = MQ . MB
 Xem đáp án
Xem đáp án
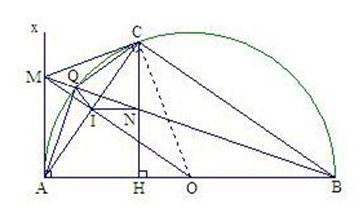
Nối A với Q, ta có: (góc nội tiếp chắn nửa đường tròn)
Lại có tam giác ABM vuông tại A
Þ AQ ^ BM
Xét ΔAMB vuông tại A có:
AQ ^ BM
Þ MA2 = MQ . MB (theo hệ thức lượng trong tam giác vuông)
Vậy MA2 = MQ . MB
Câu 68:
Cho tam giác ABC cân tại A, I là giao điểm các đường phân giác trong tam giác. Chứng minh AC là tiếp tuyến của đường tròn tâm O ngoại tiếp tam giác BIC.
 Xem đáp án
Xem đáp án
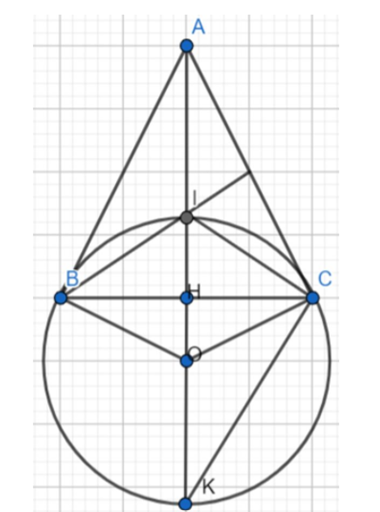
Vì ΔABC cân tại A nên AI vừa là đường phân giác vừa là đường cao
Do đó ba điểm A, I, O thẳng hàng
Þ AO ⊥ BC
(1)
Vì OI = OC = R nên ΔIOC cân tại O
(2)
CI là phân giác của :
(3)
Từ (1); (2) và (3) ta có:
Þ AC ^ CO
Vậy AC là tiếp tuyến của đường tròn tâm O ngoại tiếp tam giác BIC.
Câu 69:
Cho tam giác ABC cân tại A, I là giao điểm các đường phân giác trong tam giác. Gọi H là trung điểm của BC, IK là đường kính của đường tròn tâm O. Chứng minh: AI . HK = AK . HI.
 Xem đáp án
Xem đáp án
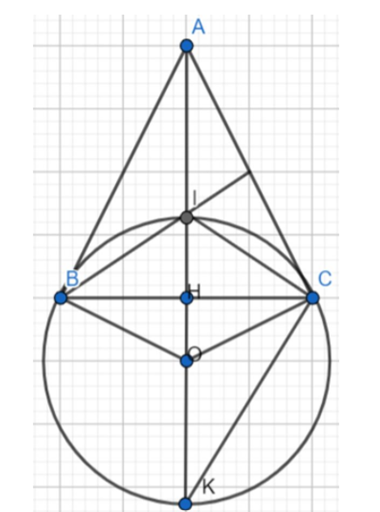
Xét ΔABC có:
CI là phân giác của
CK ^ CI
Þ CK là đường phân giác góc ngoài
(tính chất đường phân giác)
Þ AI. HK = AK. HI (đpcm)
Vậy AI. HK = AK. HI
Câu 70:
Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác ANEB là hình thang vuông.
 Xem đáp án
Xem đáp án
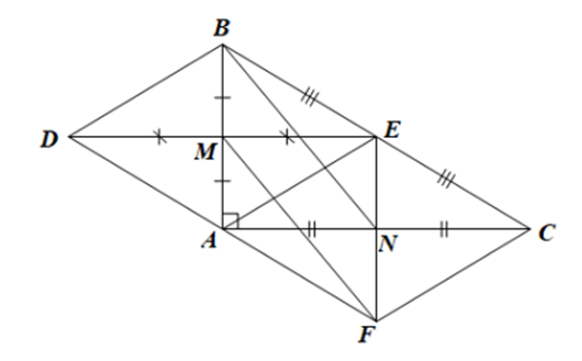
Xét ΔABC vuông tại A có AE là đường trung tuyến ứng với cạnh huyền BC
Suy ra
Vì EA = EC nên E nằm trên đường trung trực của AC.
Vì N là trung điểm của AC nên N nằm trên đường trung trực của AC.
Suy ra EN là đường trung trực của đoạn thẳng AC nên EN ⊥ AC.
Ta có: BA ⊥ AC và EN ⊥ AC nên BA // EN.
Tứ giác ANEB có BA // EN nên ANEB là hình thang
Lại có nên hình thang ANEB là hình thang vuông
Vậy ANEB là hình thang vuông.
Câu 71:
Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác ANEM là hình chữ nhật.
 Xem đáp án
Xem đáp án
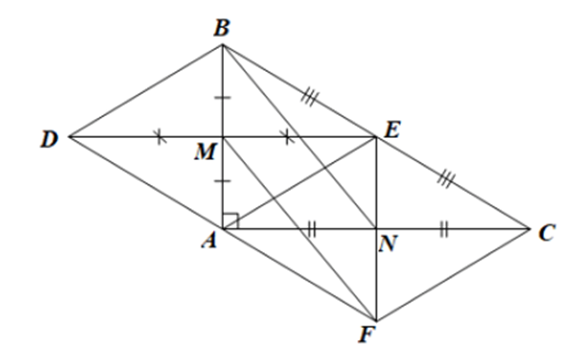
Xét ΔABC vuông tại A có:
AE là đường trung tuyến ứng với cạnh huyền BC
Suy ra
Ta có: EA = EC nên E nằm trên đường trung trực của AC.
N là trung điểm của AC nên N nằm trên đường trung trực của AC.
Þ EN là đường trung trực của đoạn thẳng AC nên EN ⊥ AC
Lại có: EA = EB nên E nằm trên đường trung trực của AB.
M là trung điểm của AB nên M nằm trên đường trung trực của AB.
Þ EM là đường trung trực của AB nên EM ⊥ AB hay 0
Tứ giác AMEN có:
Þ ANEM là hình chữ nhật
Vậy ANEM là hình chữ nhật.
