Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 31)
-
2056 lượt thi
-
97 câu hỏi
-
120 phút
Danh sách câu hỏi
Câu 1:
Một ô tô trong khoảng 1,5 giờ đầu, mỗi giờ đi được 55 km và trong hai giờ sau, mỗi giờ đi được 49,5 km. Hỏi ô tô đi được quãng đường dài bao nhiêu ki–lô–mét?
 Xem đáp án
Xem đáp án
Quãng đường ô tô đi trong 1,5 giờ đầu tiên là:
55 × 1,5 = 82,5 (km)
Quãng đường ô tô đi trong 2 giờ sau là:
49,5 × 2 = 99 (km)
Quãng đường ô tô đã đi được là:
82,5 + 99 = 181,5 (km)
Đáp số: 181,5 km
Câu 2:
Một điểm nằm trên đường thẳng y = 3x – 7 có hoành độ gấp đôi tung độ. Vậy hoành độ của điểm đó có giá trị là bao nhiêu?
 Xem đáp án
Xem đáp án
Hoành độ gấp đôi tung độ: x = 2y
Do điểm này nằm trên đường thẳng y = 3x – 7 nên có:
y = 3 . 2y – 7
y = 6y – 7
y = 1,4
Thay y = 1,4 vào y = 3x – 7 ⇒ x = 2,8.
Câu 3:
Cho hàm số: có đồ thị là (P). Điểm trên (P) (khác gốc tọa độ O(0; 0)) có tung độ gấp ba lần hoành độ thì có hoành độ là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi điểm M (x; y) là điểm cần tìm.
Vì M có tung độ gấp ba lần hoành độ nên M (x; 3x)
Thay tọa độ điểm M vào hàm số ta được:
Vậy điểm trên (P) (khác gốc tọa độ O(0; 0)) có tung độ gấp ba lần hoành độ thì có hoành độ là .
Câu 4:
Phân số sẽ thay đổi như thế nào nếu mẫu số giảm đi 6 lần và tử số giữ nguyên.
 Xem đáp án
Xem đáp án
Gọi phân số đã cho là .
Nếu mẫu số giảm đi 6 lần thì phân số sẽ có dạng
Ta có:
Vậy phân số tăng lên 6 lần.
Câu 5:
Cho số . Số lượng ước của 150 là bao nhiêu?
 Xem đáp án
Xem đáp án
Nếu với a, b, c là số nguyên tố thì m có (x + 1). (y + 1). (z + 1) ước.
Ta có: với x = 1; y = 1; z = 2
Vậy số lượng ước của 150 là:
(1 + 1). (1 + 1). (2 + 1) = 12 (ước).
Câu 6:
 Xem đáp án
Xem đáp án
144 ⋮ a; 192 a a ∈ ƯC (144; 192)
Ta có:
ƯCLN (144; 192) =
Ư(48) = {1; 2; 3; 4; 6; 8; 12; 16; 24; 48}
Mà a > 20 a ∈ {24; 48}.
Câu 7:
 Xem đáp án
Xem đáp án
Vì trong phép chia, số dư luôn nhỏ hơn số chia. Mà theo đề bài số dư là số dư, số chia bằng 9.
Suy ra số dư bằng 8.
Vậy số bị chia là:
125 × 9 + 8 = 1133
Đáp số: 1133.
Câu 10:
Cho một số tự nhiên khi viết thêm một chữ số 0 vào bên phải số đó ta được một số mới. Trung bình cộng của số mới và số cũ là 198. Tìm số tự nhiên đó.
 Xem đáp án
Xem đáp án
Nếu ta viết thêm chữ số 0 vào bên phải số đó thì ta được số mới
Suy ra số mới gấp 10 lần lần số cũ
Tổng số mới và số cũ là:
198 × 2 = 396
Số mới là:
396 : (10 + 1) × 10 = 360
Số tự nhiên ban đầu là:
360 : 10 = 36.
Câu 11:
Hai phân số có tổng là và thương là 2. Ở dạng phân số tối giản thì phân số bé có mẫu số là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi hai phân số cần tìm lần lượt là a và b
Theo đề bài, ta có: (1)
a : b = 2 ⇒ a = 2b thay vào (1) ta có:
Vậy phân số bé là và có mẫu số là 18.
Câu 12:
Lúc 6 giờ 30 phút, ô tô thứ nhất khởi hành từ A. Đến 7 giờ ô tô thứ hai cũng khởi hành từ A với vận tốc lớn hơn vận tốc ô tô thứ nhất 8km/h. Hai xe gặp nhau lúc 10 giờ cùng ngày. Tính quãng đường đi được và vận tốc mỗi xe.
 Xem đáp án
Xem đáp án
Gọi x là vận tốc (km/h) của ô tô thứ nhất (ĐK: x > 0)
Vận tốc của ô tô thứ hai: x + 8 (km/h)
Thời gian ô tô thứ nhất đi đến lúc gặp nhau là:
10 giờ – 6 giờ 30 phút = 3 giờ 30 phút = 3, 5 giờ
Thời gian ô tô thứ hai đi đến lúc gặp nhau là:
10 giờ – 7 giờ = 3 giờ
Hai ô tô gặp nhau nên cùng quãng đường, ta có:
x. 3,5 = (x + 8) . 3
⇔ 0,5x = 24
⇔ x = 48 (km/h)
Vận tốc ô tô thứ nhất là: 48 (km/h)
Vận tốc ô tô thứ hai là: 48 + 8 = 56 (km/h)
Độ dài quãng đường đã đi: 56 . 3 = 168 (km)
Câu 13:
Người ta thu hoạch được ở hai thửa ruộng 3 tấn 6 tạ thóc. Ở thửa ruộng thứ nhất thu hoạch được ít hơn thửa ruộng thứ hai 4 tạ thóc. Hỏi mỗi thửa ruộng, người ta thu hoạch được bao nhiêu ki lô gam thóc?
 Xem đáp án
Xem đáp án
Đổi 3 tấn 6 tạ = 3600 kg
4 tạ = 400 kg
Thửa ruộng thứ nhất thu hoạch được số thóc là:
(3600 – 400) : 2 = 1600 (kg)
Thửa ruộng thứ hai thu hoạch được số thóc là:
3600 – 1600 = 2000 (kg)
Đáp số: thửa ruộng 1: 1600 kg
Thửa ruộng 2: 2000 kg.
Câu 14:
Thu hoạch từ hai thửa ruộng được 5 tấn 2 tạ thóc. Thu hoạch ở thửa ruộng thứ nhất được nhiều hơn ở thửa ruộng thứ hai là 8 tạ thóc. Hỏi thu hoạch ở mỗi thửa ruộng được bao nhiêu ki–lô–gam thóc?
 Xem đáp án
Xem đáp án
Đổi: 5 tấn 2 tạ = 52 tạ
Số thóc thu hoạch ở thửa ruộng thứ nhất là:
(52 + 8) : 2=30 (tạ)
30 tạ = 3000kg
Số thóc thu hoạch ở thửa ruộng thứ hai là:
30 − 8 = 22 (tạ)
22 tạ = 2200kg
Đáp số: Thửa ruộng thứ nhất : 3000kg thóc;
Thửa ruộng thứ hai : 2200kg thóc.
Câu 16:
8 người sơn được 3 ngôi nhà trong vòng 6 giờ. Hỏi 12 người sơn được bao nhiêu ngôi nhà trong vòng 12 giờ.
 Xem đáp án
Xem đáp án
Từ giả thiết 8 người sơn được 3 ngôi nhà trong vòng 6 giờ suy ra trung bình mỗi giờ 8 người sơn được:
(ngôi nhà)
Vậy trung bình 1 người 1 giờ sơn được:
(ngôi nhà)
Do đó trong 12 giờ 12 người sẽ sơn được:
(ngôi nhà)
Đáp số: 9 ngôi nhà
Câu 17:
Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a) Tính độ dài các đoạn thẳng AB, AC, AH.
 Xem đáp án
Xem đáp án
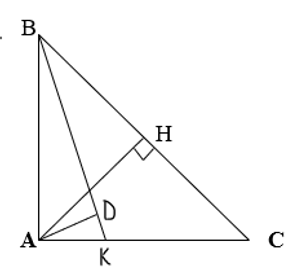
a, Áp dụng HTL tam giác:
Câu 18:
b) Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.
 Xem đáp án
Xem đáp án
b, ADHB nội tiếp
(cùng chắn AD) (1)
Có:
chung
Suy ra
Câu 19:
Cho đoạn thẳng AB, O là trung điểm của đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax, By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By tại D. Chứng minh CD = AC + BD.
 Xem đáp án
Xem đáp án
Kéo dài OC cắt BD tại K.
Khi đó:
Xét và :
OA = OB (gt)
(hai góc đối đỉnh)
Do đó: (g.c.g)
OC = OK; AC = BK (cạnh tương ứng bằng nhau)
Xét và :
OC = OK
OD là cạnh chung
(c.g.c)
Suy ra: CD = DK (cạnh tương ứng bằng nhau)
Ta có: DK = DB + BK mà AC = BK; CD = DK
Do đó: CD = AC + BD.
Câu 20:
Cho đoạn thẳng AB có độ dài 2a .Vẽ về một phía của AB các tia Ax và By vuông góc với AB. Qua trung điểm của M của AB có hai đường thẳng thay đổi luôn vuông góc với nhau và cắt Ax, By theo thứ tự tại C và D. Xác định vị trí của các điểm C, D sao cho tam giác MCD có diện tích nhỏ nhất . Tính diện tích tam giác đó.
 Xem đáp án
Xem đáp án
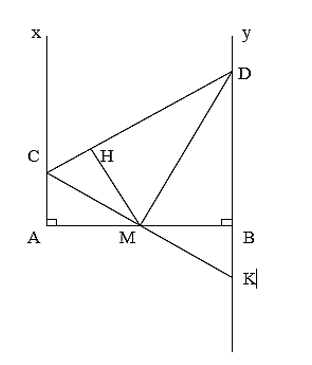
Gọi K là giao điểm của CM và DB
MA = MB; ;
Mặt khác
cân tại tại D
Kẻ
khi đó
Vậy min . Các điểm C, D được xác định trên Ax; By sao cho AC = BD = a .
Câu 21:
Có bao nhiêu số có ba chữ số chia hết cho 3?
 Xem đáp án
Xem đáp án
Số lớn nhất có 3 chữ số chia hết cho 3 là 999.
Số bé nhất có 3 chữ số chia hết cho 3 là 102.
Số số có ba chữ số chia hết cho 3 là:
(999 − 102) : 3 + 1 = 300
Đáp số: 300 số.
Câu 22:
cho tam giác vuông, biết độ dài một cạch góc vuông là 5 cm, độ dài cạnh góc vuông còn lại nhỏ hơn cạnh huyền 3cm. tính diện tích tam giác vuông đó.
 Xem đáp án
Xem đáp án
Gọi độ dài cạnh góc vuông còn lại là x
Suy ra độ dài cạnh huyền là x + 3
Theo đề, ta có:
Câu 23:
Độ dài hai cạnh góc vuông liên tiếp lần lượt là 5cm và 12 cm thì độ dài cạnh huyền là bao nhiêu?
 Xem đáp án
Xem đáp án
Áp dụng định lý Pytago vào tam giác vuông:
suy ra cạnh huyền bằng 13 cm.
Câu 24:
Để lát nền một căn phòng, người ta đã sử dụng hết 200 viên gạch hình vuông có cạnh 40cm. Hỏi căn phòng đó có diện tích bao nhiêu mét vuông, biết diện tích phần mạch vữa không đáng kể?
 Xem đáp án
Xem đáp án
Diện tích của một viên gạch lát nền là:
40 × 40 = 1600 (cm2)
Diện tích căn phòng là:
1600 × 200 = 320000 (cm2) = 32 m2
Đáp số: 32 m2.
Câu 25:
Một thửa ruộng hình chữ nhật có chiều rộng 60m, chiều dài bằng chiều rộng.
a. Tính diện tích thửa ruộng đó.
 Xem đáp án
Xem đáp án
Chiều dài thửa ruộng là:
60 : 3 × 5 = 100 (m)
a, Diện tích thửa ruộng là:
100 × 60 = 6 000 (m2)
Câu 26:
b. Biết rằng, trung bình cứ thu hoạch được 30kg thóc. Hỏi trên cả thửa ruộng đó, người ta thu hoạch được bao nhiêu tạ thóc?
 Xem đáp án
Xem đáp án
b, Số kilogam thóc người ta thu hoạch được là:
600 : 100 × 30 = 180 (kg thóc)
180 kg = 1,8 tạ
Đáp số: a, 6 000 m2
b, 1,8 tạ thóc
Câu 27:
Một huyện miền núi có 8 xã vùng thấp và 9 xã vùng cao. Mỗi xã vùng thấp được cấp 850 quyển truyện, mỗi xã vùng cao được cấp 980 quyển truyện. Hỏi truyện đó được cấp bao nhiêu quyển truyện?
 Xem đáp án
Xem đáp án
Số quyển truyện cấp cho 8 xã vùng thấp là:
850 × 8 = 6800 (quyển truyện)
Số quyển truyện cấp cho 9 xã vùng cao là:
980 × 9 = 8820 (quyển truyện)
Số quyển truyện cấp cho huyện đó là:
6800 + 8820 = 15620 (quyển truyện)
Đáp số: 15620 (quyển truyện)
Câu 28:
Một thùng phi đựng đầy dầu cân nặng 100 kg. Sau khi rót ra số dầu trong thùng thì cả dầu và thùng còn lại cân nặng 71 kg. Hãy tính xem thùng không có dầu cân nặng bao nhiêu kg?
 Xem đáp án
Xem đáp án
số dầu rót ra nặng:
100 – 71 = 29 (kg)
Cân nặng của số dầu trong thùng là:
29 × 3 = 87 (kg)
Cân nặng của thùng khi không có dầu bên trong là:
100 – 87 = 13 (kg)
Đáp số: 13 kg
Câu 29:
Một đội công nhân có 55 người nhận sửa xong một quãng đường trong 11 ngày. Hỏi muốn sửa xong quãng đường đó trong vòng 5 ngày thì cần thêm bao nhiêu công nhân nữa? (biết mức làm của các công nhân là như nhau).
 Xem đáp án
Xem đáp án
Để sửa xong quãng đường trong 1 ngày thì cần số công nhân là:
55 × 11 = 605 (công nhân)
Để sửa xong quãng đường đó trong vòng 5 ngày thì cần:
605 : 5 = 121 (công nhân)
Số công nhân cần thêm là:
121 – 55 = 66 (công nhân)
Đáp số: 66 công nhân.
Câu 30:
Số học sinh khối 6 của một trường không quá 500 em. Nếu xếp hàng 7 thì thừa ra 3 em. Còn nếu xếp hàng 6, hàng 8 hay hàng 10 thì vừa đủ. Hỏi số học sinh khối 6 của trường đó có bao nhiêu em?
 Xem đáp án
Xem đáp án
Ta có:
6 = 2 . 3
;
10 = 2 . 5
Vì số học sinh khi xếp thành hàng 6; hàng 8; hàng 10 đều vừa đủ nên số học sinh khối 6 của trường là bội chung của 6; 8; 10.
BCNN(6; 8; 10) = = 120.
BC(6; 8; 10) = {0; 120; 240; 360; 480; 600…}
Vì số học sinh không quá 500 và khi xếp hàng 7 dư 3 nghĩa là số học sinh không quá 500 em và chia cho 7 dư ra 3 học sinh.
Xét các bội chung nhỏ hơn 500 của 6; 8; 10 ta thấy chỉ có 360 chia 7 dư 3.
Vậy số học snh khối 6 của trường là 360 học sinh.
Câu 32:
Biết rằng số học sinh của khối 4 là 240 em. Hỏi số học sinh của khối 4 là bao nhiêu?
 Xem đáp án
Xem đáp án
Số học sinh khối 4 là:
240 : = 320 (học sinh)
Đáp số: 320 học sinh
Câu 33:
Cho tam giác vuông ABC, có góc A bằng 90 độ, AB = 3 cm, AC = 4 cm. D là một điểm thuộc cạnh BC, I là trung điểm của AC. E là điểm đối xứng của D qua I.
a) Tứ giác AECD là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
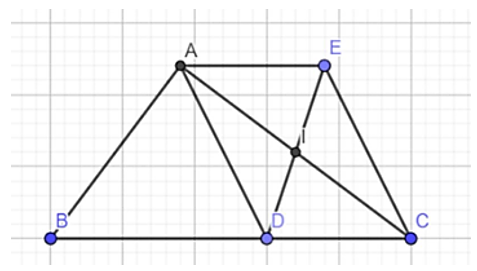
a) Xét tứ giác AECD, có:
ID = IE (E đối xứng với D qua I)
IA = IC (do I là trung điểm của AC)
Do đó, AECD là hình bình hành.
Câu 34:
b) Điểm D ở vị trí nào BC thì tứ giác AECD là hình chữ nhật. Tính độ dài cạnh của hình chữ nhật.
 Xem đáp án
Xem đáp án
b) Để AECD là hình chữ nhật ⇒ AD ⊥ CD
⇒ AD ⊥ BC
⇒ D là chân đường vuông góc hạ từ A xuống BC hay AD là đường cao của tam giác ABC.
Khi đó, theo hệ thức lượng trong tam giác vuông, ta có:
(cm)
Ta có: CD2 = AC2 – AD2 = 42 – 2,42 = 10,24 ⇒ CD = 3,2 (cm).
Câu 35:
Cho đường tròn tâm O đường kính AB. Trên AB lấy điểm E, qua E vẽ CD vuông góc với AB. Trên BE lấy điểm F, vẽ dây CM, DN đi qua F. Chứng minh tứ giác CDMN là hình thang cân.
 Xem đáp án
Xem đáp án
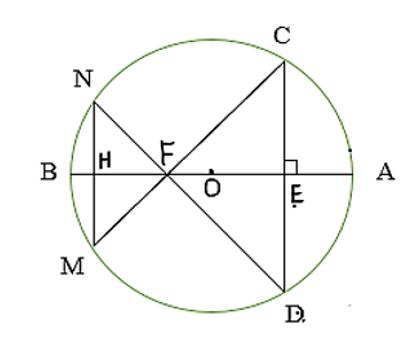
Gọi
Tứ giác CNMD nội tiếp đường tròn tâm O
(cùng chắn dây cung MN)
Xét vuông tại E và vuông tại:
EC = ED (vì AB là trung trực của CD)
EF chung.
suy ra CF = DF
Xét và :
(chứng minh trên)
CF = DF (chứng minh trên)
(hai góc đối đỉnh)
(g.c.g)
(1)
Chứng minh (c.g.c)
mà
Suy ra MN // CD ⇒ MNCD là hình thang (2)
Từ (1) và (2) ⇒ MNCD là hình thang cân.
Câu 36:
Viết các phân số theo thứ tự từ bé đến lớn.
 Xem đáp án
Xem đáp án
Các phân số theo thứ tự từ bé đến lớn là: hay .
Câu 37:
Có bao nhiêu số có 4 chữ số nhỏ hơn 2000.
 Xem đáp án
Xem đáp án
Số có 4 chữ số khác nhau nhỏ hơn 2000 có dạng
Trong đó:
a có 9 cách chọn (do không chọn chữ số 1)
b có 8 cách chọn
c có 7 cách chọn
Số các số có 4 chữ số khác nhau nhỏ hơn 2000 là:
9 × 8 × 7 = 504 (số)
Đáp số: 504 số
Câu 38:
Một mảnh đất hình chữ nhật có nửa chu vi là 64m, chiều dài bằng chiều rộng. Người ta sử dụng diện tích mảnh đất để làm nhà.
a, Tính chiều dài, chiều rộng.
 Xem đáp án
Xem đáp án
Tổng số phần bằng nhau là:
5 + 3 = 8 (phần)
Chiều dài mảnh đất là:
64 : 8 × 5 = 40 (m)
Chiều rộng mảnh đất là:
64 – 40 = 24 (m)
Câu 39:
b, Tính diện tích phần đất làm nhà.
 Xem đáp án
Xem đáp án
b, Diện tích mảnh đất là:
40 × 24 = 960 (m2)
Diện tích phần đất làm nhà là:
960 × = 80 (m2)
Đáp số: a, chiều dài 40m, chiều rộng 24m
b, Diện tích làm nhà 80 (m2)
Câu 40:
Một cửa hàng lương thực có 100 bao gạo, mỗi bao nặng 50 kg. Cửa hàng đã bán được 40 bao gạo. Hỏi cửa hàng đó còn lại bao nhiêu tấn gạo ?
 Xem đáp án
Xem đáp án
Số bao gạo cửa hàng còn lại là:
100 – 40 = 60 (bao)
Số gạo cửa hàng còn lại là:
50 × 60 = 3000 (kg)
Đổi: 3000kg = 3 tấn
Đáp số: 3 tấn gạoCâu 41:
Một lớp có 40 học sinh, trong đó mỗi học sinh giỏi ít nhất một trong hai môn Hóa và Văn, biết rằng có 25 bạn học giỏi môn Hóa, 30 bạn học giỏi môn Văn. Hỏi lớp đó có bao nhiêu học sinh giỏi cả hai môn?
 Xem đáp án
Xem đáp án
Kí hiệu A và B lần lượt là tập các học sinh học giỏi môn hóa và môn văn.
Ta có A ∪ B = 40. Theo quy tắc cộng mở rộng ta có:
n (A ∩ B) = n(A) + n(B) − n(A ∪ B) = 30 + 25 – 40 = 15
Vậy có 15 em học giỏi cả 2 môn.
Câu 42:
Người ta lát sàn gỗ một căn phòng hình chữ nhật có chiều dài 9m, chiều rộng 5m. Hỏi phải tốn bao nhiêu tiền để mua gỗ lát cả căn phòng đó? Biết giá gỗ là 250000 đồng.
 Xem đáp án
Xem đáp án
Diện tích căn phòng hình chữ nhật là:
9 × 5 = 45 ( )
Phải tốn số tiền để mua gỗ lát cả căn phòng đó là:
250000 × 45 = 11250000 (đồng)
Đáp số: 11250000 đồng
Câu 43:
Số học sinh khối 6 của một trường trong khoảng từ 450 đến 500 em. Nếu xếp mỗi hàng 6 em, 8 em hoặc 10 em thì vừa đủ. Hỏi số học sinh khối 6 của trường đó là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi số học sinh khối 6 là a (học sinh)
Vì xếp mỗi hàng 6 em, 8 em hoặc 10 em thì vừa đủ nên a ϵ BC (6; 8; 10)
6 = 2. 3
BCNN (6; 8; 10) =
BC (6; 8; 10) = B(120) = {0; 120; 240; 360; 480; 600; …}
Suy ra a = 480
Vậy số học sinh khối 6 là 480 học sinh.
Câu 44:
Số học sinh khối 6 của một trường trong khoảng từ 200 đến 400, khi xếp hàng 12, hàng 15, hàng 18 đều thừa 5 học sinh. Tính số học sinh đó.
 Xem đáp án
Xem đáp án
Gọi m (m ∈ N và 200 ≤ m ≤ 400) là số học sinh khối 6 cần tìm.
Vì khi xếp hàng 12, hàng 15, hàng 18 đều dư 5 nên ta có:
m – 5 ⋮ 12; m – 5 ⋮ 15 và m – 5 ⋮ 18.
Suy ra: m – 5 là bội chung của 12, 15 và 18
15 = 3. 5
BCNN (12; 15; 18) =
BC (12; 15; 18) = {0; 180; 360; 540; ...}
(m – 5) {0; 180; 360; 540; ...}
m {5; 185; 365; 545; ...}
Vì 200 < m < 400 suy ra: m = 365
Vậy số học sinh khối 6 là 365 em.
Câu 45:
Tìm số trung bình cộng của tất cả các số tự nhiên liên tiếp từ 1 đến 99.
 Xem đáp án
Xem đáp án
Số các số hạng từ 1 đến 99 là:
(99 – 1) : 1 + 1 = 99 (số)
Tổng các số tự nhiên liên tiếp từ 1 đến 99 là:
(99 + 1) × 99 : 2 = 4950
Trung bình cộng của các số tự nhiên liên tiếp từ 1 đến 99 là:
4950 : 99 = 50
Đáp số: 50
Câu 46:
Tìm các số tự nhiên a, b biết a + b = 135 và ƯCLN(a, b) = 27.
 Xem đáp án
Xem đáp án
ƯCLN(a, b) = 27 suy ra a = 27m; b = 27n (1); m, n là các số tự nhiên và nguyên tố cùng nhau.
a + b = 135 (2)
Thay (1) vào (2):
27m + 27n = 135
27. (m + n) = 135
m + n = 5
Vì a; b thuộc ℕ nên m ,n thuộc N
Vì m, n là các số tự nhiên và nguyên tố cùng nhau nên có các cặp (m; n) tương ứng:
TH1: n = 1; m = 4 a = 108; b = 27
TH2: n = 2; m = 3 a = 81; b = 54
TH3: n = 3; m = 2 a = 54; b = 81
TH1: n = 4; m = 1 a = 27; b = 108
Câu 47:
Tìm các số tự nhiên a, b biết a + b = 192 và ƯCLN(a, b) = 24.
 Xem đáp án
Xem đáp án
ƯCLN(a, b) = 24 suy ra a = 24p; b = 24q (1); p, q là các số tự nhiên và nguyên tố cùng nhau.
Thay a = 24p; b = 24q vào a + b = 192 ta được:
24p + 24q = 192
24 (p + q) = 192
p + q = 8.
Vì p; q là các số tự nhiên và nguyên tố cùng nhau nên có các cặp (p; q) tương ứng:
(1; 7), (7; 1), (3; 5), (5; 3).
+) Với p = 1, q = 7 thì a = 24, b = 168;
+) Với p = 7, q = 1 thì a = 168, b = 24;
+) Với p = 3, q = 5 thì a = 72, b =120;
+) Với p = 5, q = 3 thì a = 120, b = 72.
Vậy ta có các cặp (a, b) là: (168; 24), (24; 168), (72; 120), (120; 72).
Câu 48:
Từ các số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên mà mỗi số có 6 chữ số khác nhau và chữ số 2 đứng cạnh chữ số 3?
 Xem đáp án
Xem đáp án
Đặt y = 23, xét các số:
trong đó a; b; c; d; e đôi một khác nhau và thuộc tập {0; 1; y; 4; 5}.
Khi đó có 4 cách chọn a; 4 cách chọn b; 3 cách chọn c; 2 cách chọn d và 1 cách chọn e.
Theo quy tắc nhân có 4.4.3.2 = 96 số
Khi ta hoán vị trong y ta được hai số khác nhau
Nên có 96 . 2 = 192 số thỏa yêu cầu bài toán.
Câu 49:
Chu vi một thửa ruộng hình chữ nhật là 784 m. Biết rằng khi viết thêm chữ số 2 vào trước chiều rộng thì sẽ được chiều dài. Tính diện tích thửa ruộng hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Nửa chu vi hay tổng của chiều dài và chiều rộng là:
784 : 2 = 392 (m)
Theo đầu bài ta thấy chiều rộng phải là số có hai chữ số . Khi viết thêm 2 vào trước chiều rộng thì chiều rộng sẽ tăng thêm 200 đơn vị . Vậy chiều dài hơn chiều rộng là 200 m.
Chiều dài là:
(392 + 200) : 2 = 296 (m)
Chiều rộng là:
296 – 200 = 96 (m)
Diện tích hình chữ nhật đó là:
296 × 96 = 28 416 (m2)
Đáp số: 28 416 m2
Câu 50:
1 tổ công nhân dự định đắp xong 45m đường trong 15 ngày, nhưng do tích cực làm việc nên thời gian hoàn thành sớm hơn 6 ngày. Hỏi mỗi ngày công nhân làm hơn dự định bao nhiêu mét đường?
 Xem đáp án
Xem đáp án
Theo dự định mỗi ngày làm số mét là:
45 : 15 = 3(m)
Thời gian thực tế làm là:
15 – 6 = 9 (ngày)
Khi đó mỗi ngày công nhân làm số mét là:
45 : 9 = 5 (mét)
Mỗi ngày công nhân làm hơn dự định số mét là:
5 – 3 = 2 (m)
Đáp số: 2 m
Câu 51:
Cho tam giác ABC. Về phía ngoài vẽ 3 tam giác đều ABC', BCA', CAB'. Chứng minh AA', BB', CC' bằng nhau và đồng quy.
 Xem đáp án
Xem đáp án
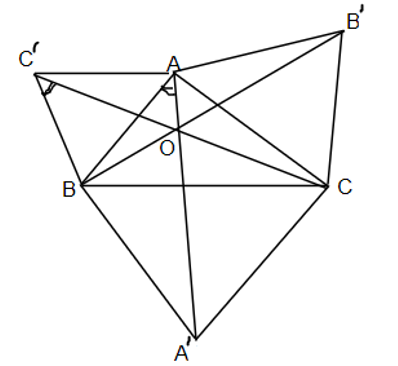
Gọi O là giao điểm của AA' và CC'. Ta chứng minh .
Ta có: vì C'B = AB, BC = BA', .
Do đó, ΔC'BC = ΔABA' (cgc).
Suy ra .
Do đó, C'BOA là tứ giác nội tiếp đường tròn.
và (cùng chắn hai cung có độ dài bằng nhau).
Tương tự ta có các góc AOB', B'OC, COA', A'OB đều bằng 60°.
Suy ra
Vậy BOB' thẳng hàng.
Vậy AA', BB', CC' đồng quy tại O.
Từ ΔC'BC = ΔABA' suy ra CC' = AA'. Chứng minh tương tự suy ra AA' = BB'.
Vậy AA' = BB' = CC'.
Câu 52:
Một tổ công nhân có 4 người dự định chuyển hết 1 kho hàng hóa trong 6 ngày, nhưng có 1 công nhân bị bệnh nên không làm việc. Hỏi kho hàng hóa đó được chuyển xong trong mấy ngày?
 Xem đáp án
Xem đáp án
Một người chuyển hết kho hàng trong:
6 . 4 = 24 (ngày)
Khi có 1 công nhân bị bệnh không làm việc được còn lại số người là:
4 – 1 = 3 (người)
Ba công nhân chuyển hết kho hàng trong số ngày là:
24 : 3 = 8 (ngày)
Đáp số: 8 ngày.
Câu 53:
Dan và Karen sống cách nhau 10 dặm và gặp nhau ở 1 quán café ở hướng bắc nhà Dan và hướng đông nhà Karen. Nếu quán cafe gần nhà Dan hơn nhà Karen 2 dặm thì từ nhà Karen tới quán bao nhiêu dặm?
 Xem đáp án
Xem đáp án
Số dặm từ nhà Karen tới quán café là:
10 – 2 = 8 (dặm)
Đáp số: 8 dặm
Câu 54:
Ba bạn An, Bình, Hà có 44 cái kẹo, số kẹo của ba bạn tỉ lệ với 5; 4; 2. Vậy An nhiều hơn Hà mấy cái kẹo?
 Xem đáp án
Xem đáp án
Gọi số kẹo của An, Bình, Hà là x; y; z (cái kẹo) (x; y; z )
Theo bài ra: x + y + z = 44
Số kẹo của ba bạn tỉ lệ với 5; 4; 2
x : y : z = 5 : 4 : 2
Theo tính chất dãy tỉ số bằng nhau:
x = 5 . 4 = 20
y = 4 . 4 =16
z = 4 . 2 = 8
Vậy An nhiều hơn Hà số kẹo là: 20 – 8 = 12 (cái kẹo)
Câu 55:
Chia số 12 thành 4 phần tỉ lệ với các số 3 5 7 9.
 Xem đáp án
Xem đáp án
Gọi x, y, z, t lần lượt là các phần tỉ lệ với 3; 5; 7; 9.
Ta được:
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
Vậy 4 phần đó lần lượt là:
Câu 56:
Cho các chữ số 1, 3, 4, 7, 8. Từ năm chữ số này có thể lập được tất cả bao nhiêu số chẵn có năm chữ số khác nhau?
 Xem đáp án
Xem đáp án
Từ những số này có thể lập được tất cả 12 số thỏa mãn, đó là:
13784; 17384; 71384; 73184; 37184; 31784;
13748; 17348; 71348; 73148; 37148; 31748.
Câu 57:
Chứng tỏ rằng nếu p là số nguyên tố lớn hơn 3 và 2p + 1 cũng là số nguyên tố thì 4p + 1 hợp số.
 Xem đáp án
Xem đáp án
Vì p là số nguyên tố lớn hơn 3, nên p = 3k + 1 hoặc p = 3k + 2 ( )
Nếu p = 3k + 1 thì 2p + 1 = 2(3k + 1) + 1 = 6k + 3 chia hết cho 3 (vô lý) vì 2p + 1 là số nguyên tố.
Vậy p = 3k + 2. Khi đó 4p + 1 = 4(3k + 2) + 1 = 12k + 9 3
Suy ra 4p + 1 là hợp số.
Câu 58:
Một cano xuôi dòng từ A đến B với vận tốc 50km/h, đi ngược dòng từ B về A với vận tốc 40km/h. Biết thời gian đi xuôi dòng ít hơn thời gian đi ngược dòng là 30 phút. Tính độ dài quãng đường AB.
 Xem đáp án
Xem đáp án
Tỉ số vận tốc khi xuôi dòng và khi ngược dòng là :
Tỉ số thời gian khi xuôi dòng và khi ngược dòng là
Đổi 30 phút = 0,5 giờ
Thời gian ca nô xuôi dòng từ A đến B là :
0,5 : (5 – 4) × 4 = 2 (giờ)
Quãng đường AB dài là:
50 × 2 = 100 (km)
Đáp số: 100 km.
Câu 59:
Cho . Chữ số thích hợp viết vào ô trống là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì 9 > 8 nên 13967 > 13867. Vậy chữ số cần điền là 9.
Câu 60:
Trên các cạnh của một miếng đất hình chữ nhật có chiều dài 2877 m và chiều rộng 1869 m người ta dự định trồng những cây cách đều nhau (mỗi gốc có 1 cây). Hỏi có bao nhiêu cách trồng cây? Cách trồng cây nào cần số cây ít nhất? Tính số cây lúc đó.
 Xem đáp án
Xem đáp án
Gọi a là khoảng cách giữa hai cây.
Vì các cây cách đều nhau nên a là ước chung của 2877 và 1869.
Ta có: 2877 = 3 . 7 . 137 và 1869 = 3 . 7 . 89.
Suy ra ƯCLN(2877, 1869) = 3 . 7 = 21.
Do đó, a = Ư(21) = {1; 3; 7; 21}.
Vậy có 4 cách trồng cây, đó là trồng cây cách đều nhau với khoảng cách 1 m, hoặc 3 m, hoặc 7 m, hoặc 21 m.
Để số cây trồng là ít nhất thì khoảng cách giữa hai cây phải lớn nhất, tức a = 21. Khi đó,Câu 61:
Cho đường thẳng (d): y = (m – 2)x + 3 với m là tham số. Hỏi (d) luôn đi qua điểm nào với mọi giá trị của m?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Với x = 0 ta luôn có y = (m – 2) . 0 + 3 = 3 với mọi m.
Do đó, đường thẳng (d) luôn đi qua điểm có tọa độ (0; 3) với mọi giá trị của m.
Câu 62:
Có 100 quyển vở và 90 cái bút bi. Cô giáo chủ nhiệm muốn chia số vở và bút thành một số phần thưởng như nhau gồm cả vở và bút để phát thưởng cho học sinh. Như vậy còn lại 4 quyển vở và 18 bút bi không thể chia đều cho các học sinh. Tính số học sinh được thưởng.
 Xem đáp án
Xem đáp án
Số bút bi được chia đều cho các học sinh là:
90 – 18 = 72 (bút)
Số quyển vở được chia đều cho các học sinh là:
100 – 4 = 96 (quyển)
Số học sinh được thưởng là ƯC(96; 72) và số học sinh lớn hơn 18.
Vậy số học sinh được thưởng là 24 học sinh.
Câu 63:
Có thể lập được bao nhiêu số tự nhiên có 4 chữ số luôn có mặt chữ số 1.
 Xem đáp án
Xem đáp án
Gọi số cần lập là (a ∈ {1; 2; ...; 9}; b, c, d ∈ {0; 1; ...; 9}).
Vì luôn có mặt chữ số 1 nên ta có 2 trường hợp sau:
TH1: a = 1, khi đó có 10 cách chọn b, 10 cách chọn c và 10 cách chọn d.
Suy ra có 103 = 1000 số thỏa mãn.
TH2: a ≠ 1, a có 8 cách chọn.
Có 3 cách chọn vị trí bắt buộc để có mặt chữ số 1 là ở b hoặc c hoặc d.
Hai chữ số còn lại, mỗi chữ số có 10 cách chọn.
Suy ra trường hợp này có 8 . 3 . 102 = 2400 số thỏa mãn.
Vậy có tất cả 1000 + 2400 = 3400 số thỏa mãn.
Câu 64:
Mua 15 quyển vở hết 60 000 đồng. Hỏi mua 20 quyển vở như vậy hết bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Mua 1 quyển vở hết số tiền là:
60 000 : 15 = 4000 (đồng)
Mua 20 quyển vở hết số tiền là:
4000 × 20 = 80 000 (đồng)
Đáp số: 80 000 đồng.
Câu 65:
Chị an chia kẹo cho các em bé. Nếu chia cho mỗi em 3 viên thì thừa 2 viên, nếu chia cho mỗi em 4 viên thì thiếu 2 viên. Hỏi chị Lan có bao nhiêu viên kẹo và có bao nhiêu em bé được chia kẹo?
 Xem đáp án
Xem đáp án
Vì nếu mỗi người được 3 viên thì thừa 2 viên, mỗi người 4 viên thì thiếu 2 viên, nên ta có:
Số kẹo đủ để chia cho 1 em 4 viên nhiều hơn số kẹo đủ chia cho 1 em 3 viên là:
2 + 2 = 4 (viên)
1 em chia 4 viên nhiều hơn 1 em chia 3 viên là:
4 – 3 = 1 (viên)
Số em được chia kẹo là:
4 : 1 = 4 (em)
Số kẹo là: 3 × 4 + 2 = 14 (viên)
Câu 66:
Trong 1 lớp học nếu xếp 3 học sinh ngồi cùng 1 bàn thì có 4 em không có chỗ ngồi, nếu xếp 4 học sinh ngồi vào 1 bộ bàn ghế thì còn dư 2 bộ bàn ghế. Hỏi lớp có bao nhiêu bộ bàn ghế và có bao nhiêu học sinh?
 Xem đáp án
Xem đáp án
Nếu xếp mỗi bàn 4 bạn và bỏ 2 bàn trống thì số học sinh dư ra:
4 × 2 + 1 = 9 (học sinh)
Lấy 9 học sinh này thêm vào mỗi bàn 1 bạn (5 bạn) vẫn còn dư 2 bàn:
Số bàn là: 9 + 2 = 11 (bàn)
Số học sinh là:
11 × 4 + 1 = 45 (học sinh)
Câu 67:
Chứng minh rằng: n(n + 1) không là số chính phương.
 Xem đáp án
Xem đáp án
Ta có: và
hay n(n + 1) không là số chính phươngCâu 68:
Một đội công nhân, trong 3 ngày đầu, mỗi ngày sửa được 2,05km đường tàu, 5 ngày sau, mỗi ngày sửa được 2,17km đường tàu. Hỏi trung bình mỗi ngày đội công nhân đó sửa được bai nhiêu ki – lô – mét đường tàu?
 Xem đáp án
Xem đáp án
Số ki – lô –mét đường tàu đội công nhân sửa trong 3 ngày:
2,05 × 3 = 6,15 (km)
Số ki –lô –mét đường tàu đội công nhân sửa trong 5 ngày:
2,17 × 5 = 10,85 (km)
Số ki – lô – mét đường tàu đội công nhân sửa trong 8 ngày:
6,15 + 10,85 = 17(km)
Trung bình mỗi ngày đội công nhân đó sửa được:
17 : 8 = 2,125 (km)
Đáp số: 2,125 km.
Câu 69:
Một căn phòng hình chữ nhật có chiều dài hơn chiều rộng 4m, chiều rộng bằng chiều dài. Người ta lát nền phòng bằng gạch men hình vuông có cạnh 2dm. Hỏi cần bao nhiêu viên gạch men để lát kín phòng đó (không tính mạch vữa).
 Xem đáp án
Xem đáp án
Chiều rộng căn phòng là:
4 : (4 – 3) × 3 = 12 (m)
Chiều dài căn phòng là:
12 + 4 = 16 (m)
Diện tích căn phòng là:
12 × 16 = 192
Diện tích 1 viên gạch men là:
2 × 2 = 4
Đổi
Cần số gạch để lát căn phòng là:
192 : 0,04 = 4800 (viên)
Câu 70:
Một căn phòng có chiều dài là 7m và hơn chiều rộng 3m. Người ta lát căn phòng đó bằng viên gạch hình vuông có cạnh 50cm. Tính số viên gạch cần lát nền căn phòng đó, biết rằng diện tích các mạch vữa không đáng kể.
 Xem đáp án
Xem đáp án
Chiều rộng căn phòng đó là:
7 – 3 = 4 (m)
Diện tích căn phòng là:
7 × 4 = 28
Đổi
Diện tích viên gạch men là:
50 × 50 = 2500
Cần số viên gạch để lát kín nền căn phòng này là:
280000 : 2500 = 112 (viên)
Câu 71:
Trung bình cộng của hai số là 65, biết rằng một trong hai số đó là 80. Tìm số còn lại.
 Xem đáp án
Xem đáp án
Tổng hai số là:
65 × 2 = 130
Số còn lại là:
130 – 80 = 50
Câu 72:
Tìm hai số có tỉ số là . Biết rằng số lớn là số có 3 chữ số và nếu xóa chữ số 4 ở hàng trăm của số lớn ta được số bé.
 Xem đáp án
Xem đáp án
Ta gọi số lớn là , số bé là .
Hiệu hai số là: – = 400
Hiệu số phần bằng nhau là:
9 – 1 = 8 (phần)
Số bé là:
400 : 8 × 1 = 50
Số lớn là:
50 + 400 = 450
Đáp số: số bé: 50; số lớn: 450.
Câu 73:
 Xem đáp án
Xem đáp án
Gọi hai số phải tìm là x và y.
Theo đề bài, ta có:
Từ (1)
(2)
x = –1,2 . 12 = – 14,4
y = –1,2 . 15 = –18
vậy hai số cần tìm là: –14,4 và –18.
Câu 74:
Để chở hết số gạo của một kho phải cần 5 xe tải vận chuyển trong 9 giờ. Hỏi muốn vận chuyển hết số gạo ở kho trong 5 giờ thì phải bổ sung thêm mấy xe tải như thế? (biết sức chở của mỗi xe là như nhau).
 Xem đáp án
Xem đáp án
1 xe tải vận chuyển hết số gạo trong:
9 × 5 = 45 (giờ)
Để vận chuyển hết số gạo trong 5 giờ cần số xe là:
45 : 5 = 9 (xe)
Phải bổ sung thêm số xe là:
9 – 5 = 4 (xe)
Đáp số: 4 xe.
Câu 75:
Một cửa hàng bán một số mét vải trong 3 ngày. Ngày thứ nhất bán số mét vải. Ngày thứ hai bán số mét vải còn lại. Ngày thứ ba bán nốt 40 mét vải. Tính tổng số mét vải của hàng đã bán.
 Xem đáp án
Xem đáp án
Số vải còn lại sau ngày bán thứ nhất bằng:
(tổng số)
Số vải bán trong ngày thứ hai bằng :
(tổng số)
Số vải bán trong ngày thứ ba bằng:
(tổng số)
tổng số mét vải này chính là 40 m.
Vậy tổng số mét vải cửa hàng đã bán là :
= 140 (m)
Câu 77:
 Xem đáp án
Xem đáp án
Ta có: x ⋮ 5
x thuộc B(5)
B(5) = {0; 5; 10; 15; 20; 25; 30;…}
Vì x thuộc B(5) và x nhỏ hơn hoặc bằng 30
x ∈ {0; 5; 10; 15; 20; 25; 30}
Câu 78:
Tìm x thuộc ℕ biết x chia hết cho 9, chia hết cho 15 và 100 < x < 150.
 Xem đáp án
Xem đáp án
x chia hết cho 9, x chia hết cho 15 nên x ∈ BC(9; 15)
Ta có:
15 = 3.5
BCNN(9; 15) =
BC(9;15) = {0; 45; 90; 135; 180;…}
Vì 100 < x < 150 suy ra x = 135.
Câu 79:
Tìm x, biết:
a) 2x3 + 4 = 58;
b) (5 – x)5 = 32;
 Xem đáp án
Xem đáp án
a) 2x3 + 4 = 58
2x3 = 58 – 4
2x3 = 54
x3 = 27
Mà 27 = 33.
Vậy x = 3.
b) (5 – x)5 = 32
Vì 32 = 25
Do đó, (5 – x)5 = 25, suy ra 5 – x = 2, suy ra x = 3.
Câu 80:
Tìm x, biết:
c) (5x – 6)3 = 64;
d) (3x)3 = (2x + 1)3.
 Xem đáp án
Xem đáp án
c) (5x – 6)3 = 64
Vì 64 = 43. Khi đó ta có
(5x – 6)3 = 43
Suy ra 5x – 6 = 4
5x = 10
x = 2
Vậy x = 2.
d) (3x)3 = (2x + 1)3
Suy ra 3x = 2x + 1
3x – 2x = 1
x = 1
Vậy x = 1.
Câu 81:
Tìm n để (25n + 3) 53.
 Xem đáp án
Xem đáp án
(25n + 3) 53
⇒ 25n + 3 – 53 53
⇒ 25n – 50 ⋮ 53
⇒ 25 (n – 2) 53
⇒ n – 2 53 (vì ƯCLN (25; 53) = 1)
⇒ n – 2 = 53k ( )
⇒ n = 53k + 2
Vậy n có dạng 53k + 2 khi 25n + 3 53Câu 82:
Cho ΔABC và điểm M ∈ AB. Gọi N là trung điểm AC. Trên tia MN lấy điểm P sao cho NP = MN. Chứng minh:
a) MC // AP và MC = AP
 Xem đáp án
Xem đáp án
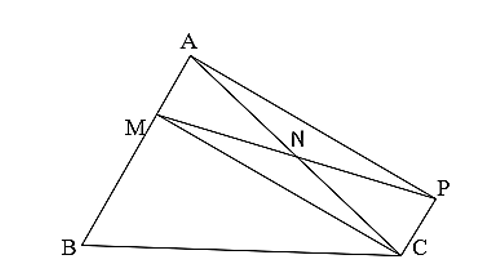
a, Vì N là trung điểm của AC
suy ra AN = CN
Xét và :
AN = CN
MN = NP
(hai góc đối đỉnh)
⇒ MC = AP và mà hai góc này so le trong
⇒ MC // AP
Câu 83:
Chứng minh:
b) PC // AM và PC = AM.
 Xem đáp án
Xem đáp án
b)
Xét và có:
AN = CN
NO = MN
(hai góc đối đỉnh)
(c.g.c)
PC = AM và mà hai góc này so le trong
⇒ PC // AM.
Câu 84:
Có 26 con vừa gà vừa chó, biết số chân gà nhiều hơn chân chó là 16 chân. Hỏi có bao nhiêu con gà, bao nhiêu con chó?
 Xem đáp án
Xem đáp án
Gọi số con gà là x, số con chó là y. Theo đề bài ta có: x + y = 26 => x = 26 – y
Vì số chân gà nhiều hơn chân chó là 16 chân nên: 2x – 4y = 16
⇒ 2. (26 – y) – 4y = 16
52 – 2y – 4y = 16
52 – 6y = 16
6y = 36
y = 6
Số gà là: 26 – 6 = 20 (con)
Vậy có 20 con gà, 6 con chó.
Câu 85:
Diện tích của một tam giác là 27 cm2, biết rằng tỉ số giữa một cạnh và đường cao tương ứng của tam giác là 1,5. Tính độ dài cạnh và đường cao nói trên.
 Xem đáp án
Xem đáp án
Giả sử đường cao là a thì cạnh tương ứng với nó sẽ là 1,5a (a > 0)
Diện tích tam giác:
Độ dài cạnh tương ứng là: 1,5 . 6 = 9 (cm)
Vậy cạnh của tam giác là 9cm và đường cao tương ứng là 6cm.
Câu 86:
Hình vuông có diện tích là 81 cm2. Một hình chữ nhật có chu vi bằng chu vi hình vuông và chiều dài hơn chiều rộng 8 cm. Tính chiều rộng, chiều dài hình chữ nhật?
 Xem đáp án
Xem đáp án
81 = 9 × 9
Cạnh của hình vuông là: 9 cm
Chu vi của HCN chính là chu vi của hình vuông là:
4 × 9 = 36 (cm)
Nửa chu vi của HCN là:
36 : 2 =18 (cm)
Chiều dài của HCN là:
(18 + 8) : 2 = 13 (cm)
Chiều rộng của HCN là:
18 – 13 = 5 (cm)
Đáp số: 13cm và 5cm.
Câu 87:
Một đội văn nghệ gồm 80 nam và 96 nữ được chia thành từng tổ sao cho số nam và số nữ được chia đều vào các tổ. Hỏi có bao nhiêu cách chia tổ?
 Xem đáp án
Xem đáp án
Gọi số cách chia tổ là a.
Vì 80 học sinh nam và 96 học sinh nữ chia đều vào các tổ nên 80 chia hết cho a, 96 chia hết cho a
⇒ a ∈ ƯC (80; 96)
Ta có:
ƯCLN (80; 96) = = 16
Số ƯC của 80 và 96 là:: 4 + 1 = 5 (cách)
Vậy có 5 cách chia tổ.
Câu 88:
Số thứ nhất là 180, số thứ hai là x. Số trung bình cộng của hai số trên là 100. Tính x.
 Xem đáp án
Xem đáp án
Tổng hai số là: 100 × 2 = 200
Theo đề bài ra ta có:
180 + x = 200
x = 200 – 180
x = 20
Câu 89:
Tìm ba số tự nhiên khác nhau biết trung bình cộng của ba số đó là 2.
 Xem đáp án
Xem đáp án
Tổng của ba số đó là:
2 × 3 = 6
Ba số tự nhiên khác nhau có tổng là 6 là:
1; 2; 3 hoặc 0; 1; 5 hoặc 0; 2; 4
Câu 90:
Có bao nhiêu số có 9 chữ số chỉ là số chẵn?
 Xem đáp án
Xem đáp án
Số chẵn lớn nhất có 9 chữ số là: 999 999 998
Số chẵn nhỏ nhất có 9 chữ số là: 100 000 000
Số các số chẵn có 9 chữ số là:
(999 999 998 – 100 000 000) : 2 + 1 = 450 000 000 (số)Câu 91:
Có bao nhiêu số chẵn có 3 chữ số?
 Xem đáp án
Xem đáp án
Số chẵn lớn nhất có 3 chữ số là: 998
Số chẵn nhỏ nhất có 3 chữ số là: 100
Số các số chẵn có 3 chữ số là:
(998 – 100) : 2 +1 = 500 (số)
Câu 92:
Tổng của 124,2 và 27,91 hơn hiệu của chúng lá bao nhiêu?
 Xem đáp án
Xem đáp án
Tổng của 124,2 và 27,91 là: 124,2 + 27,91 = 152,11
Hiệu của 124,2 và 27,91 là: 124,2 – 27,91 = 96,29
Tổng hơn hiệu là: 152,11 – 96,29 = 55,82
Đáp số: 55,82
Câu 93:
Cho hình thang ABCD có AB // CD (AB < CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với hai đáy của hình thang cắt hai đường chéo BD và AC tại E và F, cắt BC tại N. Chứng minh rằng N, E, F lần lượt là trung điểm của BC, BD, AC.
 Xem đáp án
Xem đáp án
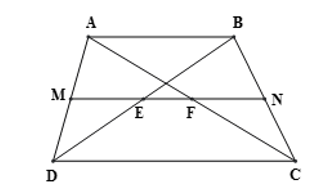
Xét hình thang ABCD có:
MA = MD
N ∈ BC
MN // AB // CD
Suy ra N là trung điểm của BC.
Xét có:
MA = MD; MF // DC
⇒ FA = FC ⇒ F là trung điểm của AC.
Xét có:
MA = MD; ME // AB
⇒ DE = BE ⇒ E là trung điểm của BDCâu 94:
Lớp 5A có 35 học sinh tham gia trồng cây. Tổ 1 có 12 em trồng được 48 cây. Nếu số cây mỗi học sinh trồng được như nhau thì lớp 5A trồng được bao nhiêu cây?
 Xem đáp án
Xem đáp án
Mỗi học sinh trồng được số cây là:
48 : 12 = 4 (cây)
Lớp 5A trồng được số cây là:
35 × 4 = 140 (cây)
Đáp số: 140 cây
Câu 95:
Tìm số tự nhiên biết trung bình cộng của hai số là 79, một trong hai số bằng 38.
 Xem đáp án
Xem đáp án
Tổng hai số là:
79 × 2 = 158
Số tự nhiên còn lại là:
158 – 38 = 120
Đáp số: 120
Câu 96:
Tổ công nhân có 5 người trong 6 ngày sản xuất được 360 sản phẩm. Hỏi tổ công nhân khác có 15 người, trong 3 ngày sản xuất được bao nhiêu sản phẩm? (biết năng suất mỗi công nhân là như nhau).
 Xem đáp án
Xem đáp án
Trong 1 ngày tổ công nhân thứ nhất sản xuất được số sản phẩm là:
360 : 6 = 60 (sản phẩm)
Một người làm được số sản phẩm là:
60 : 5 = 12 (sản phẩm)
Tổ công nhân khác có 15 người thì 1 ngày làm được số sản phẩm là:
12 × 15 = 180 (sản phẩm)
Trong 3 ngày thì sản xuất được:
180 × 3 = 540 (sản phẩm)
Đáp số: 540 sản phẩm.
Câu 97:
Một công nhân mỗi ngày làm được 5 sản phẩm. Hỏi sau 16 ngày người công nhân đó làm được bao nhiêu sản phẩm? Biết mỗi ngày người công nhân đó làm được số sản phẩm là như nhau.
 Xem đáp án
Xem đáp án
Sau 16 ngày người công nhân đó sản xuất được số sản phẩm là:
16 × 5 = 80 (sản phẩm)
Đáp số: 80 sản phẩm.
