39 câu hỏi trắc nghiệm thuộc 80 câu trắc nghiệm: Thể tích khối đa diện (có đáp án) (P1) - hamchoi.vn

80 câu trắc nghiệm: Thể tích khối đa diện (có đáp án)

80 câu trắc nghiệm: Thể tích khối đa diện (có đáp án) (P1)

1165 lượt thi
39 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

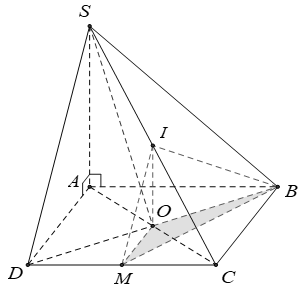
Tính thể tích V của hình chóp S.ABC có đáy là tam giác đều có cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng $\sqrt{3}$ $\frac{\sqrt{3} a}{4}$ . Thể tích của hình chóp S.ABC là:

A. $V = \frac{\sqrt{3} a^{3}}{8}$

B. $V = \frac{\sqrt{2} a^{3}}{12}$

C. $V = \frac{\sqrt{3} a^{3}}{12}$

D. $V = \frac{\sqrt{3} a^{3}}{24}$

Đáp án D

Gọi M là trung điểm của BC, H là chân đường vuông góc kẻ từ A đến SM. Khi đó khoảng cách từ A đến mặt phẳng (SBC) bằng AH. Ta có:

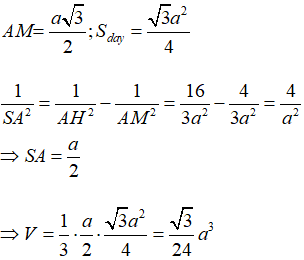
Câu 2:

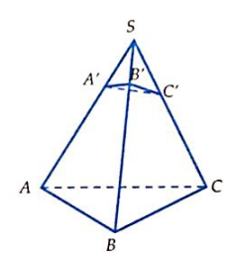
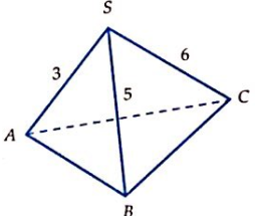
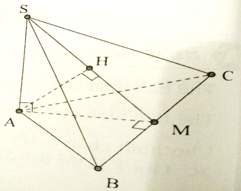
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = $\frac{a}{2}$ , SC = BC = $a \sqrt{22}$ $\sqrt{2}$ . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số $k = \frac{V'}{V}$

A. $k = \frac{1}{3}$

B. $k = \frac{\sqrt{2}}{4}$

C. $k = \frac{4}{9}$

D. $k = \frac{2}{3}$

Đáp án C

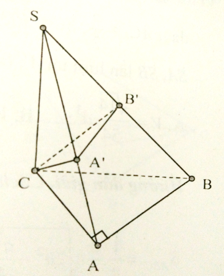
Do CS = CB nên B’ là trung điểm của SB.

Ta có:

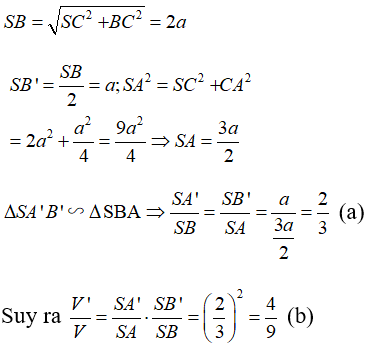
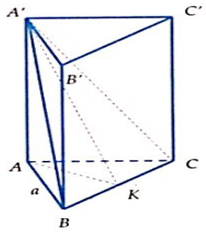
Câu 3:

Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = $\frac{a}{2}$ , SC = BC = $a \sqrt{2}$ . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Tính thể tích V của hình chóp S.A’B’C.

A. $V = \frac{\sqrt{14}}{54} a^{3}$

B. $V = \frac{\sqrt{14}}{64} a^{3}$

C. $V = \frac{\sqrt{14}}{49} a^{3}$

D. $V = \frac{4}{61} a^{3}$

Đáp án A

Áp dụng ví dụ 2, ta có:

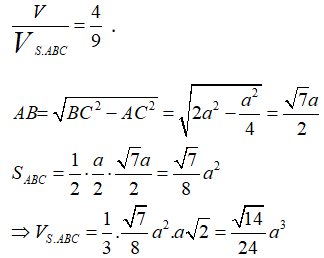
Từ đó suy ra

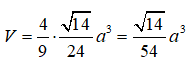
Câu 4:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng $a \sqrt{2}$ , tam giác SAD cân tại S, mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích S.ABCD bằng $\frac{4 a^{3}}{3}$ . Tính khoảng cách h từ B đến mặt phẳng (SCD).

A. $h = \frac{2}{3} a$

B. $h = \frac{4}{3} a$

C. $h = \frac{8}{3} a$

D. $h = \frac{3}{4} a$

Đáp án B

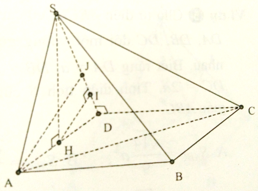
Gọi H là trung điểm của AD, vì ΔASD cân ở S nên SH ⊥ AD.

Vì (SAD)⊥(ABCD) nên SH ⊥ (ABCD). Kẻ HI ⊥ SD.

Vì DC ⊥ AD, DC ⊥ SH nên DC ⊥ (SAD). Do đó DC ⊥ HI.

Kết hợp với HI ⊥ SD, suy ra HI ⊥ (SDC).

Vì AB // (SDC) nên d(B; (SDC)) = d(A; (SDC)) = 2HI

Ta có

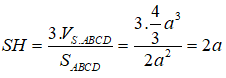
Ta lại có

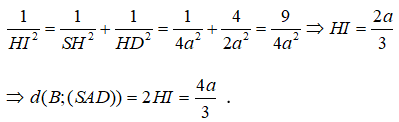
Câu 5:

Cho tứ diện ABCD, có các cạnh DA, DB, DC đôi một vuông góc với nhau. Biết rằng DA = a, DB = $a \sqrt{2}$ , DC = 2a. Tính diện tích S của tam giác ABC.

A. $S_{A B C} = \frac{\sqrt{14}}{9} a^{2}$

B. $S_{A B C} = \frac{\sqrt{14}}{6} a^{2}$

C. $S_{A B C} = \frac{\sqrt{14}}{4} a^{2}$

D. $S_{A B C} = \frac{\sqrt{14}}{2} a^{2}$

Đáp án D

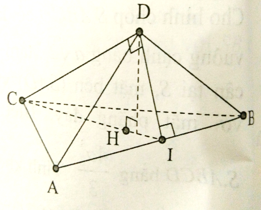
Kẻ DI ⊥ AB, DH ⊥ CI. Khi đó DH ⊥ (BCA).

Suy ra

Câu 6:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng $a \sqrt{2}$ $\sqrt{2}$ . Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại E, I, F. Tính tỉ số k giữa thể tích hình chóp S.AEIF và thể tích hình chóp S.ABCD.

A. $k = \frac{1}{4}$

B. $k = \frac{1}{3}$

C. $k = \frac{1}{6}$

D. $k = \frac{2}{9}$

Đáp án B

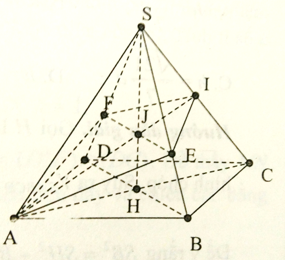
Do các cạnh bên bằng nhau nên hình chiếu của S lên (ABCD) phải trùng với tâm H của hình vuông ABCD.

Do ABCD là hình vuông có cạnh bằng a nên đường chéo BD = $a \sqrt{2}$

Suy ra $∆ S B D$ đều $\Rightarrow$ I là trung điểm của SC.

Gọi J là giao điểm của AI và SH

vì BD ⊥ SC, nên BD//(P). Từ J kẻ đường thẳng song song với BD cắt SB tại E, cắt SD tại F

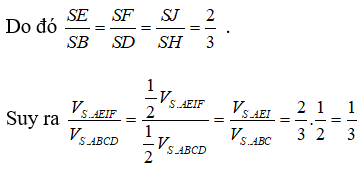
Câu 7:

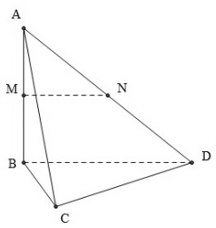
Cho hình chóp S.ABCD có đáy là hình chữ nhật, hình chiếu của S lên đáy trùng với trung điểm của AB. Tính thể tích V của hình chóp đã cho, biết rằng AB = a, BC = $a \sqrt{6}$ $\sqrt{6}$ , khoảng cách từ A đến mặt (SCD) bằng $\sqrt{6}$ $\frac{a \sqrt{6}}{3}$

A. $\frac{a^{3} \sqrt{6}}{6}$

B. $\frac{a^{3} \sqrt{2}}{4}$

C. $\frac{a^{3} \sqrt{2}}{2}$

D. $\frac{a^{3} \sqrt{2}}{6}$

Đáp án C

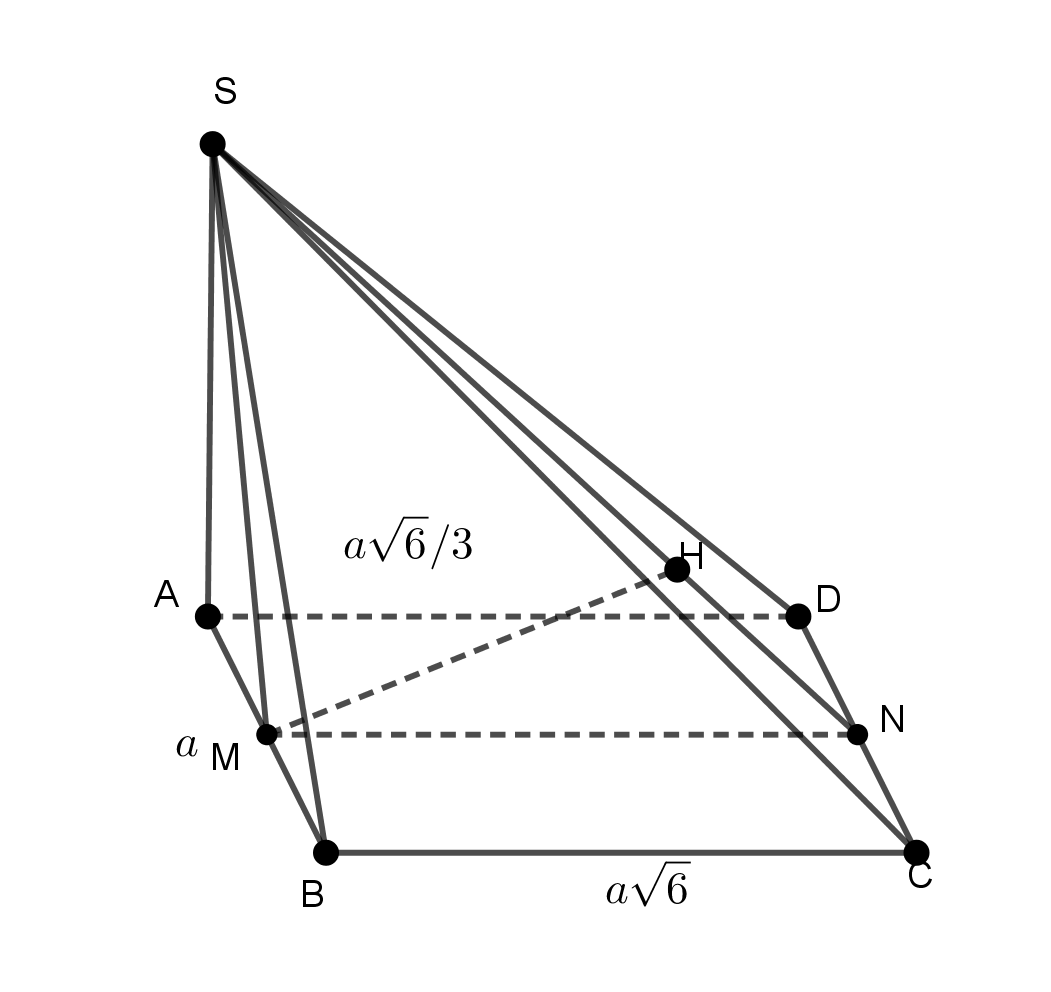
Gọi M, N lần lượt là trung điểm của AB, CD, H là chân đường vuông góc kẻ từ M tới SN. Khi đó SM ⊥ (ABCD). Vì AB // CD nên AB // (SCD), do đó d(A, (SCD)) = d(M, (SCD)) = MH

Ta có

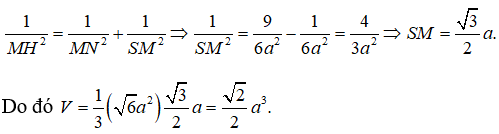
Câu 8:

Cho hình chóp S.ABCD, có đáy là hình vuông cạnh a, SCD là tam giác đều và (SCD) vuông góc với đáy. Tính khoảng cách h từ A đến mặt phẳng (SBD).

A. $h = \frac{3 a}{7}$

B. $h = \frac{2 \sqrt{3} a}{7}$

C. $h = \frac{\sqrt{21} a}{7}$

D. $h = \frac{\sqrt{42} a}{7}$

Đáp án C

Gọi H là trung điểm của CD, dễ thấy SH là đường cao của hình chóp.

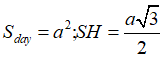
Suy ra

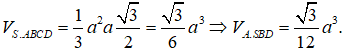
Để ý rằng ${SB}^{2} = {SH}^{2} + {BH}^{2} = {SH}^{2} + {BC}^{2} + {CH}^{2}$ = $\frac{3 a^{2}}{4} + a^{2} + \frac{a^{2}}{2}$ $3 a^{2} / 4 + a^{2} + a^{2} / 4 = 2 a^{2}$ .

Suy ra BS = BD = $a \sqrt{22}$ $\sqrt{2}$ , gọi K là trung điểm của SD ta có:

Câu 9:

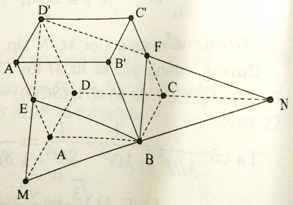
Cho hình hộp ABCD.A'B'C'D'. Gọi E, F tương ứng là trung điểm của các cạnh A’A, C’C. Gọi M = (D'E) ∩ (DA), N = (D'F) ∩ (DC). Tính tỉ số giữa thể tích hình chóp D’.DMN và thể tích hình hộp ABCD.A'B'C'D'

A. $k = \frac{1}{3}$

B. $k = \frac{2}{3}$

C. $k = \frac{3}{4}$

D. $k = 1$

Đáp án B

Dễ thấy MN đi qua B, MD = 2AD, ND = 2CD. Hình chóp và hình hộp nói trên có chung chiều cao h .

Nếu diện tích đáy của hình hộp bằng S thì diện tích đáy của hình chóp bằng 2S.

Ta có:

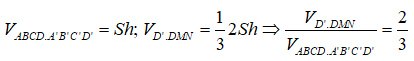
Câu 10:

Cho hình hộp ABCD.A'B'C'D'. Gọi E, F tương ứng là trung điểm các cạnh A’A, C’C. Mặt phẳng (D’EF) chia hình hộp thành hai hình đa diện. Gọi (H) là hình đa diện chứa đỉnh A, (H’) là hình đa diện còn lại. Tính tỉ số k giữa thể tích hình (H) và thể tích hình (H’).

A. $k = \frac{1}{3}$

B. $k = \frac{2}{3}$

C. $k = \frac{3}{4}$

D. $k = 1$

Đáp án D

Gọi M = D'E ∩ DA, N = D'F ∩ DC. Dễ thấy MN đi qua B, các hình chóp E.AMB và F.CNB có diện tích đáy và chiều cao bằng nhau.

Ta có:

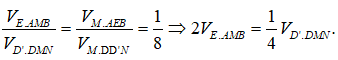
Áp dụng ví dụ 9, ta có:

Suy ra V_(H) = V_(H'). Do đó k = 1.

Câu 11:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng $60 °$ . Tính theo a thể tích khối chóp S.ABCD

A. $\frac{4 a^{3} \sqrt{3}}{3}$

B. $\frac{a^{3} \sqrt{3}}{3}$

C. $\frac{2 a^{3} \sqrt{3}}{3}$

D. $\frac{2 a^{3} \sqrt{6}}{3}$

Đáp án A

Gọi O là tâm hình vuông ABCD, M là trung điểm CD.

Khi đó SO là đường cao hình chóp, góc SMO là góc giữa mặt bên và mặt đáy của hình chóp.

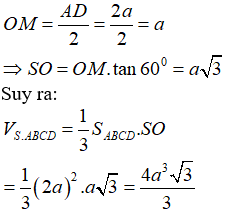
Câu 12:

Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a. Mặt bên tạo với mặt đáy một góc 60°. Tính thể tích V của hình chóp S.ABC.

A. $V = \frac{a^{3} \sqrt{3}}{2}$

B. $V = \frac{a^{3} \sqrt{3}}{6}$

C. $V = \frac{a^{3} \sqrt{3}}{12}$

D. $V = \frac{a^{3} \sqrt{3}}{24}$

Đáp án D

Gọi H là tâm của tam giác ABC. Trong (SBC), kẻ SI vuông góc BC.

Do góc giữa mặt bên và mặt đáy là $60 °$ suy ra

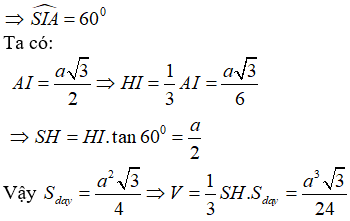
Câu 13:

Hình chóp tứ giác đều có tất cả các cạnh bằng a. Thể tích khối chóp đó bằng:

A. $\frac{a^{3} \sqrt{2}}{2}$

B. $\frac{a^{3} \sqrt{2}}{6}$

C. $\frac{a^{3} \sqrt{2}}{3}$

D. $\frac{a^{3} \sqrt{3}}{3}$

Đáp án B

Câu 14:

Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau: BA = BC = 3a, BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD Tính thể tích khối chóp C.BDNM.

A. $V = 8 a^{3}$

B. $V = \frac{2 a^{3}}{3}$

C. $V = \frac{9 a^{3}}{4}$

D. $V = a^{3}$

Câu 15:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2a. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45°. Thể tích hình chóp S.ABCD bằng

A. $\frac{\sqrt{6} a^{3}}{18}$

B. $\frac{2 \sqrt{2} a^{3}}{3}$

C. $\frac{a^{3}}{3}$

D. $\frac{2 a^{3}}{3}$

Câu 16:

Cho hình chóp tam giác đều đáy có cạnh bằng a, góc tạo bởi các mặt bên và đáy bằng 60°. Thể tích khối chóp là:

A. $V = \frac{a^{3} \sqrt{3}}{24}$

B. $V = \frac{a^{3} \sqrt{6}}{24}$

C. $V = \frac{a^{3} \sqrt{3}}{8}$

D. $V = \frac{a^{3}}{8}$

Đáp án A

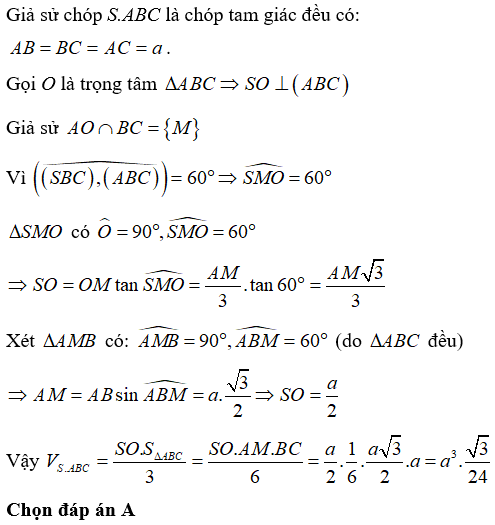
Câu 17:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = a, AC = $a \sqrt{2}$ $\sqrt{2}$ , SA vuông góc với mp đáy. Góc tạo bởi (SBC) và mặt đáy bằng 30°. Thể tích S.ABC bằng

A. $\frac{a^{3} \sqrt{2}}{4}$

B. $\frac{a^{3} \sqrt{2}}{6}$

C. $\frac{a^{3}}{9}$

D. $\frac{a^{3} \sqrt{2}}{2}$

Kẻ AH $⊥$ BC

Câu 18:

Cho khối chóp S.ABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm A', B', C' sao cho $S A' = \frac{1}{3} S A; S B' = \frac{1}{4} S B; S C' = \frac{1}{2} S C .$ Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S'.A'B'C'. Khi đó tỷ số $\frac{V'}{V}$ là:

A. 12

B. 24

C. $\frac{1}{12}$

D. $\frac{1}{24}$

Câu 19:

Cho lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60° AB = a. Khi đó thể tích của khối ABCC'B' bằng:

A. $a^{3} \sqrt{3}$

B. $\frac{3 a^{3}}{4}$

C. $\frac{\sqrt{3} a^{3}}{4}$

D. $\frac{3 a^{3} \sqrt{3}}{4}$

Câu 20:

Tính thể tích V của khối hộp chữ nhật ABCD.A'B'C'D', biết AB = a, AD = $a \sqrt{22}$ $\sqrt{2}$ và AC' hợp với đáy một góc 60°.

A. $V = 2 a^{3} \sqrt{6}$

B. $V = a^{3} \sqrt{2}$

C. $V = 3 a^{3} \sqrt{2}$

D. $V = \frac{3 a^{3} \sqrt{2}}{2}$

Câu 21:

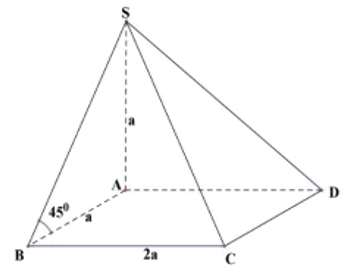
Cho hình chóp S.ABCD có SC ⊥ (ABCD), đáy ABCD là hình thoi có cạnh bằng a $\sqrt{3}$ và $\hat{ABC} = 120^{o}$ . Biết rằng góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45°. Tính theo a thể tích khối chóp S.ABCD.

A. $\frac{a^{3} \sqrt{3}}{12}$

B. $\frac{3 a^{3} \sqrt{3}}{12}$

C. $\frac{a^{3} \sqrt{3}}{4}$

D. $\frac{3 a^{3} \sqrt{3}}{4}$

Đáp án D

Câu 22:

Cho hình chóp đều S.ABCD có cạnh đáy bằng a, biết góc giữa cạnh bên và mặt đáy bằng 45°. Tính thể tích V của khối chóp S.ABCD.

A. $V = \frac{\sqrt{2}}{6} a^{3}$

B. $V = \frac{\sqrt{3}}{4} a^{3}$

C. $V = \frac{\sqrt{3}}{12} a^{3}$

D. $V = \frac{3 \sqrt{3}}{4} a^{3}$

Câu 23:

Một hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích của khối chóp đó là:

A. $\frac{a^{2}}{4} \sqrt{3 b^{2} - a^{2}}$

B. $\frac{a^{2}}{12} \sqrt{3 b^{2} - a^{2}}$

C. $\frac{a^{2}}{6} \sqrt{3 b^{2} - a^{2}}$

D. $a^{2} \sqrt{3 b^{2} - a^{2}}$

Câu 24:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy, cạnh bên SC tạo với mặt phẳng (SAB) một góc 30°. Thể tích của khối chóp đó bằng:

A. $\frac{a^{3} \sqrt{3}}{3}$

B. $\frac{a^{3} \sqrt{2}}{4}$

C. $\frac{a^{3} \sqrt{2}}{2}$

D. $\frac{a^{3} \sqrt{2}}{3}$

Câu 25:

Cho khối chóp S.ABC với SA ⊥ SB , SB ⊥ SC , SC ⊥SA . Biết độ dài SA, SB, SC lần lượt là 3, 5, 6. Thể tích của khối chóp đó bằng:

A. 20

B. 10

C. 15

D. 30

Câu 26:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a; mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông cân tại S. Tính thể tích V của khối chóp S.ABC.

A. $V = \frac{a^{3} \sqrt{3}}{12}$

B. $V = \frac{a^{3} \sqrt{3}}{24}$

C. $V = \frac{a^{3} \sqrt{3}}{6}$

D. $V = \frac{a^{3} \sqrt{3}}{8}$

Câu 27:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại đỉnh B, AB = a, SA = 2a và SA vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối tứ diện S.AHK.

A. $V = \frac{4 a^{3}}{15}$

B. $V = \frac{8 a^{3}}{45}$

C. $V = \frac{8 a^{3}}{15}$

D. $V = \frac{4 a^{3}}{5}$

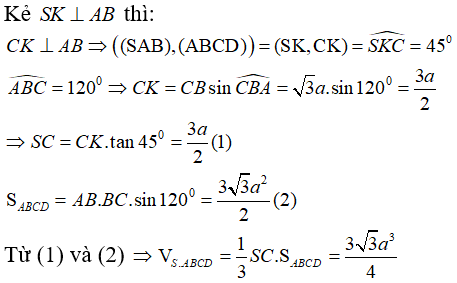
Câu 28:

Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = $a \sqrt{2}$ $\sqrt{2}$ ; SA ⊥ (ABCD), góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:

A. $a^{3} \sqrt{2}$

B. $3 a^{3}$

C. $a^{3} \sqrt{6}$

D. $3 a^{3} \sqrt{2}$

Đáp án A

Câu 29:

Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài đường cao không đổi thì thể tích S.ABC tăng lên bao nhiêu lần?

A. 4.

B. 2.

C. 3.

D. $\frac{1}{2}$ .

Đáp án A

Khi độ dài cạnh đáy tăng lên 2 lần thì diện tích đáy tăng lên 4 lần.

⇒ Thể tích khối chóp tăng lên 4 lần.

Câu 30:

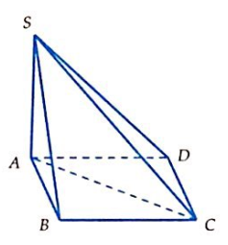
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết ΔSAB là tam giác đều và thuộc mặt phẳng vuông góc với mặt phẳng (ABC). Tính thể tích khối chóp S.ABC biết AB = a, AC = $a \sqrt{33}$ $\sqrt{3}$ .

A. $\frac{a^{3} \sqrt{6}}{12}$

B. $\frac{a^{3} \sqrt{6}}{4}$

C. $\frac{a^{3} \sqrt{2}}{6}$

D. $\frac{a^{3}}{4}$

Đáp án A

Câu 31:

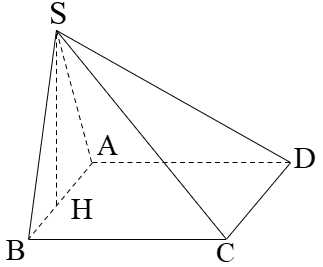
Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt bên (SAB) là tam giác vuông cân tại S và thuộc mặt phẳng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD biết BD = a, AC = $a \sqrt{3}$ $\sqrt{3}$ .

A. $a^{3}$

B. $\frac{a^{3} \sqrt{3}}{4}$

C. $\frac{a^{3} \sqrt{3}}{12}$

D. $\frac{a^{3}}{3}$

Đáp án C

Câu 32:

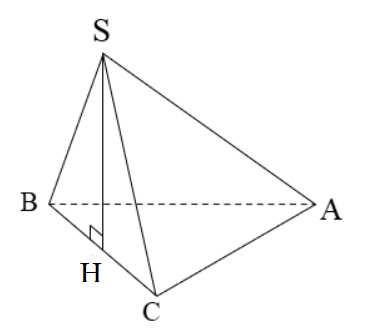
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Tính thể tích khối chóp S.ABC biết AB = a, AC = a $\sqrt{3}$ , SB = a $\sqrt{2}$ .

A. $\frac{a^{3} \sqrt{6}}{6}$

B. $\frac{a^{3} \sqrt{3}}{2}$

C. $\frac{a^{3} \sqrt{3}}{6}$

D. $\frac{a^{3} \sqrt{6}}{2}$

Đáp án C

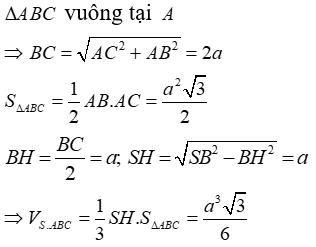
Câu 33:

Cho hình chóp S.ABCD có đáy ABCD hình vuông cạnh a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AD. Tính thể tích khối chóp S.ABCD biết SB = $\frac{3 a}{2}$ .

A. $\frac{a^{3}}{3}$

B. $a^{3}$

C. $\frac{a^{3}}{2}$

D. $\frac{3 a^{3}}{2}$

Đáp án A

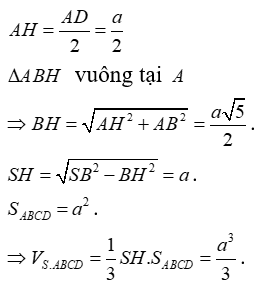
Câu 34:

Hình chóp S.ABCD đáy là hình vuông cạnh a, SD = $\frac{a \sqrt{13}}{2}$ . Hình chiếu của S lên (ABCD) là trung điểm H của AB. Thể tích khối chóp là

A. $\frac{a^{3} \sqrt{2}}{3}$

B. $\frac{2 a^{3}}{3}$

C. $a^{3} \sqrt{12}$

D. $\frac{a^{3}}{3}$

Đáp án A

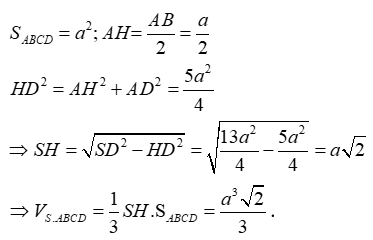
Câu 35:

Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, $A D = a \sqrt{2}$ $\sqrt{2}$ , SA⊥(ABCD) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:

A. $a^{3} \sqrt{2}$

B. $3 a^{3} \sqrt{2}$

C. $3 a^{3}$

D. $a^{3} \sqrt{6}$

Đáp án A

Theo bài ra ta có:

SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).

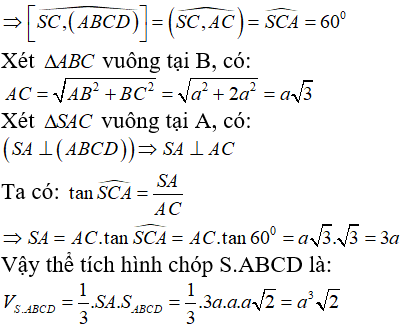
Câu 36:

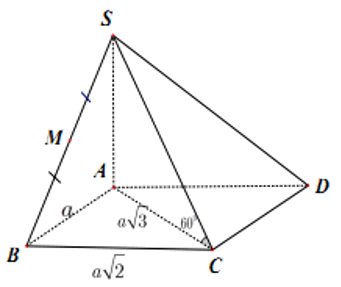
Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, $A D = a \sqrt{2}$ $\sqrt{2}$ , SA⊥(ABCD) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:

A. $a^{3} \sqrt{2}$

B. $a^{3} \sqrt{6}$

C. $3 a^{3}$

D. $3 a^{3} \sqrt{2}$

SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).

Xét ΔABC vuông tại B, có

Câu 37:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh BC = a $\sqrt{2}$ , cạnh bên SA vuông góc với mặt phẳng đáy; mặt bên (SBC) tạo với mặt đáy (ABC) một góc bằng 45°. Thể tích khối chóp S.ABC theo a bằng

A. $\frac{a^{3} \sqrt{2}}{6}$

B. $\frac{a^{3} \sqrt{2}}{2}$

C. $\frac{a^{3} \sqrt{2}}{4}$

D. $\frac{a^{3} \sqrt{2}}{12}$

Đáp án D

Gọi M là trung điểm của BC

Vì $∆ A B C$ cân tại A nên $A M ⊥ B C$

Ta có: $S A ⊥ (A B C D) \Rightarrow S A ⊥ B C$

Mà $A M ⊥ B C$

nên $B C ⊥ (S A M) \Rightarrow B C ⊥ S M \Rightarrow \hat{((S B C); (A B C D))} = \hat{S M A} = 45 °$

Xét $∆ A B C$ vuông cân tại A, có $B C = a \sqrt{2}$

$B C = a \sqrt{2}$ $B C = a \sqrt{2}$

$B C = a \sqrt{2}$

$\tan \hat{S A M} = \frac{S A}{A M}$

Câu 38:

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC cân tại A. Cạnh bên SB lần lượt tạo với mặt phẳng đáy, mặt phẳng trung trực của BC các góc bằng 30° và 45°, khoảng cách từ S đến cạnh BC bằng a. Tính thể tích khối chóp S.ABC

A. $V = a^{3}$

B. $V = \frac{a^{3}}{2}$

C. $V = \frac{a^{3}}{3}$

D. $V = \frac{a^{3}}{6}$

Câu 39:

Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM.

A. $\frac{a^{3}}{24}$

B. $\frac{3 a^{3}}{24}$

C. $\frac{a^{3} \sqrt{3}}{24}$

D. $\frac{a^{3} \sqrt{2}}{24}$

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương