Trắc nghiệm Sự đồng biến, nghịch biến của hàm số có đáp án
-
1067 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số y = f (x) xác định và có đạo hàm trên R. Chọn kết luận đúng:
 Xem đáp án
Xem đáp án
Ta có: và nên hàm số đồng biến trên R.
Đáp án cần chọn là: A
Câu 2:
Cho hàm số y = f (x) nghịch biến và có đạo hàm trên (-5;5). Khi đó:
 Xem đáp án
Xem đáp án
Vì y = f(x) nghịch biến trên (-5;5) nên
Vậy
Đáp án cần chọn là: B
Câu 3:
Cho hàm số y = f (x) có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng:
 Xem đáp án
Xem đáp án
A, B sai vì hàm số chỉ nghịch biến trên các khoảng và (0;2)
D sai vì hàm số chỉ đồng biến trên khoảng và
C đúng vì giá trị thấp nhất của y trên bảng biến thiên là 0.
Đáp án cần chọn là: C
Câu 4:
Cho hàm số y = f (x) có bảng biến thiên như sau:
Hàm số y = f (x) nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Quan sát bảng biến thiên ta thấy hàm số nghịch biến trên các khoảng và
Mà khoảng nằm trong khoảng (- 2;0) nên hàm số đã cho cũng nghịch biến trên
Đáp án cần chọn là: A
Câu 5:
Cho hàm số y = f (x) xác định liên tục trên , có bảng biến thiên như hình sau. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên ta thấy:
Hàm số đồng biến trên
Hàm số đồng biến trên do đó cũng đồng biến trên
Trên các khoảng và hàm số không đơn điệu (đồng biến hay nghịch biến)
Đáp án cần chọn là: B
Câu 6:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số nghịch biến trên khoảng
 Xem đáp án
Xem đáp án
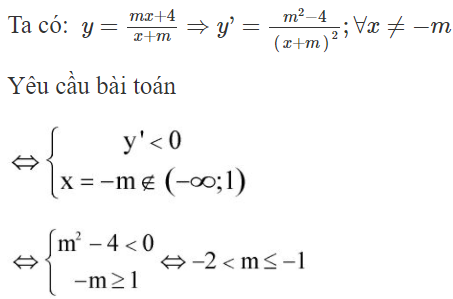
Đáp án cần chọn là: D
Câu 7:
Tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng là:
 Xem đáp án
Xem đáp án
ĐKXĐ:
Ta có:
Để hàm số đồng biến trên thì
Vậy
Đáp án cần chọn là: D
Câu 9:
Cho hàm số đa thức f (x) có đạo hàm trên R. Biết và đồ thị hàm số như hình sau:
Hàm số đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đặt ta có
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng
Vẽ đồ thị hàm số và đường thẳng trên cùng mặt phẳng tọa độ ta có:
Dựa vào đồ thị hàm số ta thấy
Khi đó ta có BBT hàm số
Khi đó ta suy ra được BBT hàm số như sau:
Dựa vào BBT và các đáp án ta thấy hàm số g (x) đồng biến trên (0;4)
Đáp án cần chọn là: B
Câu 10:
Cho hàm số f (x) có đạo hàm liên tục trên R và . Đồ thị hàm số như hình bên. Có bao nhiêu số nguyên dương a để hàm số nghịch biến trên ?
 Xem đáp án
Xem đáp án
Ta có:
Đặt , với thì
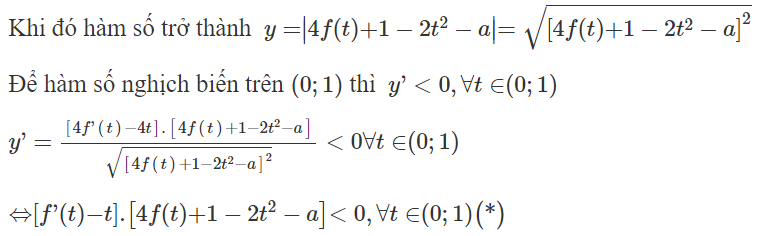
Vẽ đồ thị hàm số y = f ' (t) và y = t trên cùng mặt phẳng tọa độ ta có:
Dựa vào đồ thị hàm số ta thấy trên (0;1) đường thẳng y = t luôn nằm phải trên đồ thị hàm số y = f ' (t), do đó
Đặt
Ta có:
Bắt đầu thi ngay