Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 83)
-
1383 lượt thi
-
43 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho x > 0, y > 0 và x + y ≥ 6. Tìm GTNN của biểu thức:
\[P = 5x + 3y + \frac{{12}}{x} + \frac{{16}}{y}\].
 Xem đáp án
Xem đáp án
\[P = 5x + 3y + \frac{{12}}{x} + \frac{{16}}{y}\]
\( = 3x + \frac{{12}}{x} + y + \frac{{16}}{y} + 2\left( {x + y} \right)\)
Áp dụng Cô-si, ta có:
\(3x + \frac{{12}}{x} \ge 2\sqrt {3x.\frac{{12}}{x}} = 2.6 = 12\)
\(y + \frac{{16}}{y} \ge 2\sqrt {y.\frac{{16}}{y}} = 8\)
Lại có 2(x + y) ≥ 12
Nên P ≥ 12 + 8 + 12 = 32
Dấu “=” xảy ra khi:
\(\left\{ \begin{array}{l}3x = \frac{{12}}{x}\\y = \frac{{16}}{y}\\x + y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 4\end{array} \right.\).
Vậy Pmin = 32 khi x = 2 và y = 4.
Câu 2:
Tìm x ∈ ℤ, biết:
a) (x + 2)(x – 4) ≥ 0;
b) \(\frac{{2x + 3}}{{x + 4}} > 1\).
 Xem đáp án
Xem đáp án
a) (x + 2)(x – 4) ≥ 0
\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x + 2 \ge 0\\x - 4 \le 0\end{array} \right.\\\left\{ \begin{array}{l}x + 2 \le 0\\x - 4 \ge 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge - 2\\x \le 4\end{array} \right.\\\left\{ \begin{array}{l}x \le - 2\\x \ge 4\end{array} \right.\end{array} \right.\)
⇔ −2 ≤ x ≤ 4
Vì x ∈ ℤ nên x ∈ {−2; −1; 0; 1; 2; 3; 4}.
b) \(\frac{{2x + 3}}{{x + 4}} < 1\)
\( \Leftrightarrow \frac{{2x + 3}}{{x + 4}} - 1 < 0\)
\( \Leftrightarrow \frac{{2x + 3 - x - 4}}{{x + 4}} < 0\)
\( \Leftrightarrow \frac{{x - 1}}{{x + 4}} < 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 1 > 0\\x + 4 < 0\end{array} \right.\\\left\{ \begin{array}{l}x - 1 < 0\\x + 4 > 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 1\\x < - 4\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\x > - 4\end{array} \right.\end{array} \right.\)
⇔ −4 < x < 1
Vì x ∈ ℤ nên x ∈ {−3; −2; −1; 0}
Câu 3:
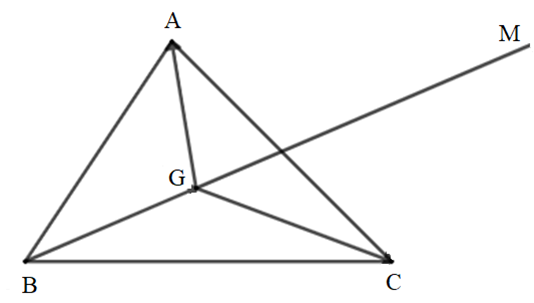
Cho tam giác ABC. Hãy xác định điểm M thỏa mãn điều kiện:
\(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
 Xem đáp án
Xem đáp án
Gọi G là trọng tâm ∆ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
Ta có: \(VT = \overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} \)
\( = \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MB} \)
\( = \overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} - 2\overrightarrow {MB} \)
\( = 3\overrightarrow {MG} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) - 2\overrightarrow {MB} \)
\( = 3\overrightarrow {MG} - 2\overrightarrow {MB} \)
\( = \overrightarrow {MG} + 2\overrightarrow {MG} - 2\overrightarrow {MB} \)
\( = \overrightarrow {MG} - 2\overrightarrow {GM} - 2\overrightarrow {MB} \)
\( = \overrightarrow {MG} - 2\left( {\overrightarrow {GM} + \overrightarrow {MB} } \right)\)
\( = \overrightarrow {MG} - 2\overrightarrow {GB} = VP = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {MG} = 2\overrightarrow {GB} \)
Hay \(\overrightarrow {GM} = 2\overrightarrow {GB} \)
Trên đường thẳng BG lấy điểm M sao cho GM = 2BG thì điểm M sẽ thỏa mãn đề bài.
Câu 4:
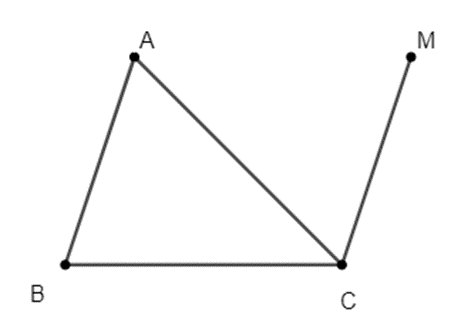
Cho tam giác ABC. Tìm điểm M thỏa mãn điều kiện:
\(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
 Xem đáp án
Xem đáp án
\(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
\( \Leftrightarrow \left( {\overrightarrow {MA} - \overrightarrow {MB} } \right) - \overrightarrow {CM} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CM} \)
Hay M là đỉnh của hình bình hành ABCM.
Câu 5:
Một xe chạy trọng 2,5 giờ. 1 giờ đầu xe chạy với tốc độ trung bình 60 km/h, 1,5 giờ sau xe chạy với tốc trung bình 40 km/h. Tính tốc độ trung bình của xe trông suốt thời gian chuyển động?
 Xem đáp án
Xem đáp án
Tốc độ trung bình của xe trong toàn bộ khoảng thời gian chuyển động là:
\({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{{v_1}{t_1} + {v_2}{t_2}}}{{{t_1} + {t_2}}} = \frac{{1.60 + 1,5.40}}{{2,5}} = 48\) (km/h)
Đáp số: 48 km/h.
Câu 6:
Một xe chạy trong 5 giờ: 2 giờ đầu xe chạy với tốc độ trung bình 60 km/h; 3 giờ sau xe chạy với tốc độ trung bình 40 km/h. Tốc độ trung bình của xe trong suốt thời gian chuyển động là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quãng đường xe đi được trong 2 giờ đầu là: s1 = 60.2 = 120 (km)
Quãng đường xe đi được trong 3 giờ sau là: s2 = 40.3 = 120 (km)
Tốc độ trung bình của xe là: v = 240 : 5 = 48 (km/h)
Đáp số: 48 km/h.
Câu 7:
Cho phương trình ẩn x: (m – 1)x2 – 2mx + m + 1 = 0 (1) (m là tham số)
a) Xác định m để phương trình (1) có nghiệm x1 và x2.
b) Tìm m để phương trình (1) có nghiệm x1; x2 thỏa mãn x1 + x2 – x1x2 = 3.
 Xem đáp án
Xem đáp án
a) Phương trình (1) có hai nghiệm phân biệt x1; x2 khi và chỉ khi:
\(\left\{ \begin{array}{l}x - 1 \ne 0\\\Delta ' > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\{m^2} - \left( {m - 1} \right)\left( {m + 1} \right) > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\{m^2} - {m^2} + 1 > 0\end{array} \right.\)
⇔ m ≠ 1
Vậy với m ≠ 1 thì thỏa mãn yêu cầu bài toán.
b) Áp dụng định lí Vi-ét, ta có:
\(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{2m}}{{m - 1}}\\{x_1}{x_2} = \frac{{m + 1}}{{m - 1}}\end{array} \right.\) (*)
Ta có: x12 + x22 – x1x2 = 3
⇔ (x1 + x2)2 – 3x1x2 = 3
Thay (*) vào ta có:
\({\left( {\frac{{2m}}{{m - 1}}} \right)^2} - 3.\frac{{m + 1}}{{m - 1}} = 3\)
\( \Leftrightarrow \frac{{4{m^2}}}{{{{\left( {m - 1} \right)}^2}}} - \frac{{3m + 3}}{{m - 1}} = 3\)
⇔ 4m2 – (3m + 3)(m – 1) = 3(m – 1)2
⇔ 4m2 – 3(m2 – 1) = 3(m2 – 2m + 1)
⇔ 4m2 – 3m2 + 3 = 3m2 – 6m + 3
⇔ 2m2 – 6m = 0
⇔ 2m(m – 3) = 0
\( \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 3\end{array} \right.\) (thỏa mãn m ≠ 1)
Vậy với m = 0 hoặc m = 3 thì thỏa mãn yêu cầu bài toán.
Câu 8:
Cho bất phương trình (m – 1)x2 + 2mx – 3 > 0 (*). Tìm giá trị của m để phương trình nghiệm đúng với mọi x ∈ ℝ.
 Xem đáp án
Xem đáp án
TH1: m = 1 khi đó (*) trở thành:
2x – 3 > 0 ⇔ \(x > \frac{3}{2}\) (loại)
TH2: m ≠ 1 ta có:
Xét ∆’ = m2 – (m – 1)(−3)
= m2 + 3m + 3
Để bất phương trình có nghiệm đúng với mọi x thì:
\(\left\{ \begin{array}{l}m - 1 < 0\\\Delta ' < 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m < 1\\{m^2} + 3m + 3 < 0\forall m \in \mathbb{R}\end{array} \right.\)
⇔ m < 1
Vậy với m < 1 thì thỏa mãn yêu cầu bài toán.
Câu 9:
Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là A.
Ta có: cos2a = cos2a – sin2a = 2cos2a – 1 = 1 – 2sin2a.
Câu 10:
Cho tam giác ABC chứng minh rằng:
\(\cos \widehat A + \cos \widehat B - \cos \widehat C = 4\cos \frac{{\widehat A}}{2}.\cos \frac{{\widehat B}}{2}.\sin \frac{{\widehat C}}{2} - 1\)
 Xem đáp án
Xem đáp án
\(VT = \cos \widehat A + \cos \widehat B - \cos \widehat C\)
\( = 2\cos \frac{{\widehat A + \widehat B}}{2}.\cos \frac{{\widehat A - \widehat B}}{2} + 2{\sin ^2}\frac{{\widehat C}}{2} - 1\)
\( = 2\sin \frac{{\widehat C}}{2}.\cos \frac{{\widehat A - \widehat B}}{2} + 2{\sin ^2}\frac{{\widehat C}}{2} - 1\)
\( = 2\sin \frac{{\widehat C}}{2}\left( {\cos \frac{{\widehat A - \widehat B}}{2} + \sin \frac{{\widehat C}}{2}} \right) - 1\)
\( = 2\sin \frac{{\widehat C}}{2}\left( {\cos \frac{{\widehat A - \widehat B}}{2} + \cos \frac{{\widehat A + \widehat B}}{2}} \right) - 1\)
\( = 4.\cos \frac{{\widehat A}}{2}.\cos \frac{{\widehat B}}{2}.\sin \frac{{\widehat C}}{2} - 1\).
Câu 11:
Cho tam giác ABC vuông tại A (AB < AC). Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Chứng minh tứ giác AMIN là hình chữ nhật.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác AICD là hình thoi.
c) Cho AC = 20 cm, BC = 25 cm. Tính diện tích ΔABC.
 Xem đáp án
Xem đáp án
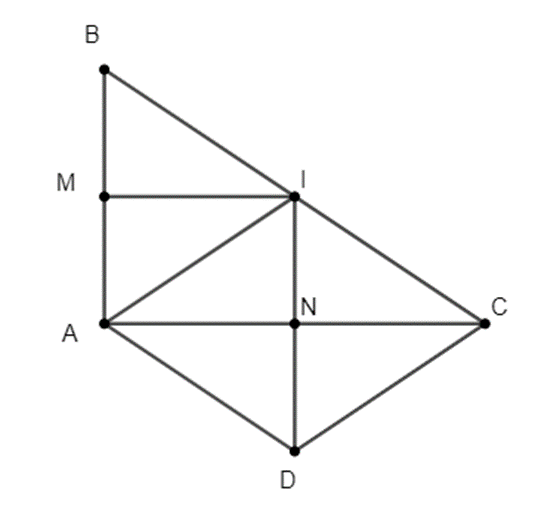
a) Xét tứ giác AMIN có:
\[\widehat {MAN} = \widehat {ANI} = \widehat {IMA} = 90^\circ \]
⇒ Tứ giác AMIN là hình chữ nhật.
b) Xét ∆ABC vuông tại A có AI là trung tuyến nên AI = IC = \(\frac{{BC}}{2}\)
Do đó ∆AIC cân có đường cao IN đông thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (tính chất đối xứng)
Nên AICD là hình bình hành.
Lại có AC⊥ID (gt). Do đó AICD là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lý py-ta-go)
⇔ AB2 = 252 – 202
⇒ AB = 15 (cm)
Vậy SABC = \(\frac{1}{2}AB.AC\)\( = \frac{1}{2}.15.20 = 150\) (cm2).
Câu 12:
Rút gọn biểu thức: \(P = \frac{{\sqrt x }}{{\sqrt x + 3}} + \frac{{2\sqrt x }}{{\sqrt x - 3}} - \frac{{3x + 9}}{{x - 9}}\).
 Xem đáp án
Xem đáp án
ĐKXĐ: x ≥ 0; x ≠ 9.
\(P = \frac{{\sqrt x }}{{\sqrt x + 3}} + \frac{{2\sqrt x }}{{\sqrt x - 3}} - \frac{{3x + 9}}{{x - 9}}\)
\( = \frac{{\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} + \frac{{2\sqrt x \left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} - \frac{{3x + 9}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\)
\( = \frac{{x - 3\sqrt x }}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} + \frac{{2x + 6\sqrt x }}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} - \frac{{3x + 9}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\)
\( = \frac{{x - 3\sqrt x + 2x + 6\sqrt x - 3x - 9}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\)
\( = \frac{{3\sqrt x + 9}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\)
\( = \frac{{3\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\)
\( = \frac{3}{{\sqrt x - 3}}\).
Câu 13:
Rút gọn biểu thức: \(B = \frac{{a + 2\sqrt a + 1}}{{\sqrt a + 1}} + \frac{{a - 1}}{{\sqrt a - 1}} - \sqrt a \).
 Xem đáp án
Xem đáp án
ĐKXĐ: a ≥ 0; a ≠ 1.
\(B = \frac{{a + 2\sqrt a + 1}}{{\sqrt a + 1}} + \frac{{a - 1}}{{\sqrt a - 1}} - \sqrt a \)
\( = \frac{{{{\left( {\sqrt a + 1} \right)}^2}}}{{\sqrt a + 1}} + \frac{{\left( {\sqrt a - 1} \right)\left( {\sqrt a + 1} \right)}}{{\sqrt a - 1}} - \sqrt a \)
\( = \sqrt a + 1 + \sqrt a + 1 - \sqrt a \)\( = \sqrt a + 2\).
Câu 14:
Cho nửa đường tròn (O), đường kính BC. Kẻ tiếp tuyến Bx của nửa đường tròn (O). Trên tia đối của CB lấy điểm A. Kẻ tiếp tuyến AE cắt Bx tại D (Bx nằm trên nửa mặt phẳng bờ BC chứa nửa đường tròn (O). Gọi H là giao điểm của BE với DO; K là giao điểm thứ hai của DC với nửa đường tròn (O).
a) Chứng minh: DO // EC.
b) Chứng minh: AO.AB = AE.AD.
 Xem đáp án
Xem đáp án
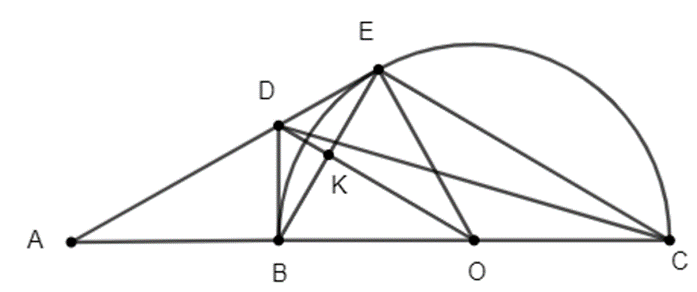
a) Ta có:
DO ⊥ BE (tính chất của 2 tiếp tuyến cắt nhau)
EC⊥ BE (Do BC là đường kính của (O))
Do đó DO // EC
b) Xét ∆AEO và ∆ ABD có:
\(\widehat A\) chung
\(\widehat {ABD} = \widehat {AEO} = 90^\circ \)
Do đó (g.g)
Suy ra\( \Rightarrow \frac{{AE}}{{AB}} = \frac{{AO}}{{AD}}\)
Vậy AO.AB = AE. AD
Câu 15:
Có bao nhiêu số tự nhiên có 3 chữ số phân biệt mà tổng các chữ số là số lẻ.
 Xem đáp án
Xem đáp án
Gọi số tự nhiên có 3 chữ số phân biệt là \(\overline {abc} \)
Tổng các chữ số là số lẻ có các trường hợp sau:
TH1: Số tự nhiên có 3 chữ số phân biệt đều là số lẻ
Chọn a, b, c lần lượt có số cách là 5, 4, 3 cách
⇒ có 5.4.3 = 60 cách
TH2: Số tự nhiên có 3 chữ số phân biệt trong đó có 2 chữ số chẵn và 1 chữ số lẻ
Nếu a lẻ thì a có 5 cách chọn
b, c lần lượt có 5, 4 cách chọn
Nếu chữ số lẻ ở hàng chục và hàng đơn vị thì
a có 4 cách chọn
Chữ số chẵn còn lại có 4 cách chọn
Chữ số lẻ có 5 cách chọn
⇒ có 5.5.4 + 2.4.4.5 = 260 cách
Vậy số số tự nhiên có 3 chữ số phân biệt tổng các chữ số là số lẻ là:
60 + 260 = 320 số.
Đáp số: 320 số.
Câu 16:
Một trường THCS có tất cả 4 lớp 7. Các em học sinh lớp 7 đã đăng kí tham gia một trong các câu lạc bộ bơi lội, cờ vua và cầu lông theo số liệu sau:
|
Lớp |
Sĩ số |
CLB Bơi Lội |
CLB Cờ vua |
CLB cầu lông |
|
7A |
42 |
14 |
12 |
10 |
|
7B |
43 |
17 |
15 |
11 |
|
7C |
40 |
11 |
13 |
9 |
|
7D |
39 |
12 |
10 |
10 |
a) Có bao nhiêu phần trăm học sinh lớp 7 tham gia câu lạc bộ bơi lội?
b) Lớp 7A có bao nhiêu phần trăm học sinh tham gia tất cả các câu lạc bộ?
c) Ở môn cờ vua thì lớp nào có tỉ lệ tham gia đông nhất?
 Xem đáp án
Xem đáp án
Tổng số học sinh của 44 lớp 77 là: 42 + 43 + 40 + 39 = 164 (học sinh)
Tổng số học sinh lớp 77 tham gia CLB bơi lội là: 14 + 17 + 11 + 12 = 54 (học sinh)
Tổng số học sinh lớp 77 tham gia CLB cờ vua là: 12 + 15 + 13 + 10 = 50 (học sinh)
Tổng số học sinh lớp 77 tham gia CLB cầu lông là: 10 + 11 + 9 + 10 = 40 (học sinh)
a) Phần trăm học sinh lớp 77 tham gia CLB bơi lội là:
\(\frac{{54}}{{164}}.100\% \approx 32,93\% \)
b) Số học sinh lớp 7A: 14 + 12 + 10 = 36 (học sinh)
Phần trăm số học sinh lớp 7A tham gia tất cả các CLB là:
\(\frac{{36}}{{164}}.100\% \approx 21,95\% \)
c) Vì 10 < 12 < 13 < 15
Nên số học sinh tham gia môn cờ vua của lớp 7B có tỉ lệ tham gia đông nhât.
Câu 17:
 Xem đáp án
Xem đáp án
Số học sinh lớp 5A đăng kí tham gia các Câu lạc bộ chiếm số phần trăm số học sinh của lớp 5A là:
\(\frac{{14}}{{35}}.100\% = 40\% \)
Đáp số: 40%
Câu 18:
Cho ∆DMN cân tại D có DM = DN = 6 cm, MN = 5 cm. Phân giác của góc M cắt DN tại I, phân giác góc N cắt DM tại K. Tính tỉ số KM và KD.
 Xem đáp án
Xem đáp án
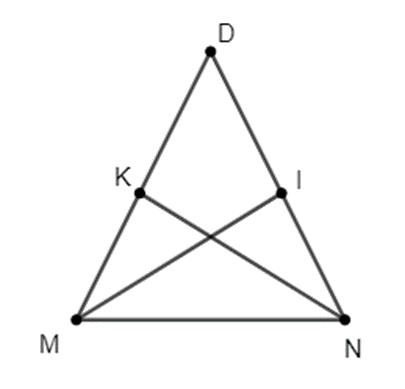
Theo tính chất của đường phân giác trong tam giác ta có:
\(\frac{{DK}}{{MK}} = \frac{{DN}}{{MN}} = \frac{6}{5}\).
Câu 19:
Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây:
|
Thời gian (s) |
0 |
0,5 |
1 |
2 |
3 |
|
Độ cao (m) |
0 |
28 |
48 |
64 |
48 |
a) Xác định hàm số bậc hai biểu thị độ cao h(m) của quả bóng gofl tính theo thời gian t(s).
b) Sau bao lâu kể từ khi vận động viên đánh bóng thì bóng lại chạm đất?
 Xem đáp án
Xem đáp án
a) Xét hàm số bậc hai biểu thị độ cao h phụ thuộc thời gian t có dạng
h(t) = at2 + bt + c, trong đó a ≠ 0. Theo đề bài:
Với t = 0, h = 0, ta có: c = 0 nên h(t) = at2 + bt. Khi đó:
+ Với t = 1, h = 48, ta có: a . 12 + b . 1 = 48 ⇔ a + b = 48.
+ Với t = 2, h = 64, ta có: a . 22 + b . 2 = 64 ⇔ 4a + 2b = 64.
Giải hệ phương trình:
\(\left\{ \begin{array}{l}a + b = 48\\4a + 2b = 64\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 16\\b = 64\end{array} \right.\)
Suy ra h(t) = –16t2 + 64t.
Thay các giá trị tương ứng còn lại của bảng vào công thức trên, ta thấy phù hợp.
Vậy hàm số bậc hai cần tìm là h(t) = –16t2 + 64t.
b) Bóng chạm đất khi h(t) = 0 ⇔ – 16t2 + 64t = 0.
Suy ra t = 0 hoặc t = 4.
Vậy sau 4 giây kể từ khi vận động viên đánh bóng thì bóng lại chạm đất.
Câu 20:
Một tổ sản xuất theo kế hoạch phải sản xuất 75 thùng khẩu trang trong một số ngày dự định. Trong thực tế, do cải tiến kĩ thuật nên mỗi ngày tổ làm vượt mức 5 thùng vì vậy không những làm được 80 thùng mà họ còn hoàn thành sớm hơn 1 ngày. Hỏi theo kế hoạch, mỗi ngày tổ đó phải sản xuất bao nhiêu thùng khẩu trang.
 Xem đáp án
Xem đáp án
Gọi số thùng khẩu trang tổ sản xuất mỗi ngày theo kế hoạc là: x (thùng/ ngày)
(ĐK: x ∈ ℕ*)
Thời gian tổ hoàn thành công việc theo kế hoạch là: \(\frac{{75}}{x}\) (ngày)
Số thùng khẩu trang tổ sản xuất mỗi ngày trong thực tế là: x + 5 (thùng/ ngày)
Thời gian tổ hoàn thành công việc trong thực tế là: \(\frac{{80}}{{x + 5}}\) (ngày)
Vì trong thực tế họ hoàn thành kế hoạch sớm hơn 1 ngày nên ta có phương trình:
\(\frac{{75}}{x} - \frac{{80}}{{x + 5}} = 1\)
\( \Leftrightarrow \frac{{75\left( {x + 5} \right)}}{{x\left( {x + 5} \right)}} - \frac{{80x}}{{\left( {x + 5} \right)x}} = \frac{{x\left( {x + 5} \right)}}{{x\left( {x + 5} \right)}}\)
⇔ 75x + 375 – 80x = x2 + 5x
⇔ −x2 – 10x + 375 = 0
⇔ x2 + 10x – 375 = 0
⇔ (x – 15)(x + 25) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x - 15 = 0\\x + 25 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 15\\x = - 25\end{array} \right.\)
Ta có: x = 15 thỏa mãn điều kiện.
Vậy theo kế hoạch, mỗi ngày tổ đó phải sản xuất 15 thùng khẩu trang.
Câu 21:
Cho hình chữ nhật ABCD có AB = 12 cm, BC = 9 cm. Bán kính R của đường tròn đi qua bốn đỉnh của hình chữ nhật là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có đường kính của đường tròn chính là đường chéo của hình chữ nhật.
Nên suy ra: \(R = \frac{{\sqrt {{{12}^2} + {9^2}} }}{2} = 7,5\) (cm)
Đáp số: 7,5 cm.
Câu 22:
Một đoàn tình nguyện đến một trường tiểu học miền nùi để trao tặng 20 suất quà cho 10 em học sinh nghèo học giỏi. Trong 20 suất quà đó gồm 7 chiếc áo mùa đồng, 9 thùng sữa tươi và 4 chiếc cặp sách. Tất cả các suất quà đề có giá trị tương đương nhau. Biết rằng mỗi em nhận 2 suất quà khác loạ (Ví dụ: 1 chiếc áo mùa đồng và 1 thùng sữa tươi). Trong số các em được nhận quà có hai em Việt và Nam. Xác suất để hai em Việt và Nam đó nhận được suất quà giống nhau bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Với 3 loại quà khác loại ta chia được thành 3 nhóm tương ứng như sau:
Nhóm (1) gồm 1 áo và 1 sữa
Nhóm (2) gồm 1 sữa và 1 cặp
Nhóm (3) gồm 1 cặp và 1 áo
Gọi x,y,z lần lượt là số học sinh nhận các suất quà thuộc nhóm (1); (2); (3)
Ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y + z = 10\\x + z = 7\\x + y = 9\\y + z = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = 3\\z = 1\end{array} \right.\)
Vậy số cách chia 10 suất quà này cho 10 học sinh là \(C_{10}^6.C_4^3.C_1^1\)
Để Việt và Nam có các phần thưởng giống nhau có các TH sau:
TH1: Việt và Nam nhận suất quà nhóm (1) có \(C_8^4.C_4^3.C_1^1\)
TH2: Việt và Nam nhận suất quà nhóm (2) có \(C_8^6.C_2^1.C_1^1\)
Tổng số cách để Việt và Nam có suất quà giống nhau là: \(C_8^4.C_4^3.C_1^1 + C_8^6.C_2^1.C_1^1\)
Vậy xác suất cần tìm là: \(P = \frac{{C_8^4.C_4^3.C_1^1 + C_8^6.C_2^1.C_1^1}}{{C_{10}^6.C_4^3.C_1^1}} = \frac{2}{5}\)
Câu 23:
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm. Tính khoảng các từ tâm O đến dây AB.
 Xem đáp án
Xem đáp án
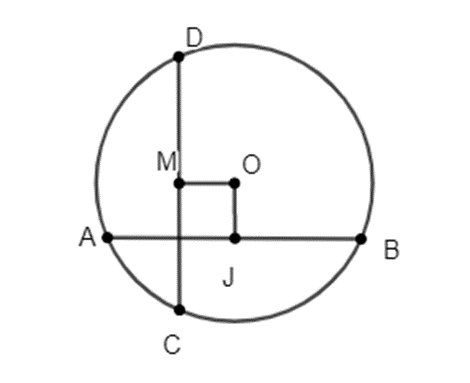
Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
Ta được \(AJ = \frac{1}{2}AB = 4\) (cm)
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
Do đó OJ = 3 (cm)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
Câu 24:
Tìm giá trị lớn nhất của hàm số: y = 3x2 + x – 1 trên đoạn [−1; 1].
 Xem đáp án
Xem đáp án
y’ = 6x + 1
⇒ y’ = 0
\( \Leftrightarrow x = \frac{{ - 1}}{6}\)
y(−1) = 1; y(1) = 3; \(y\left( { - \frac{1}{6}} \right) = - 1\)
⇒ Min = −1
Câu 25:
 Xem đáp án
Xem đáp án
Tập xác định: D = ℝ.
Hàm số y = 2x3 + 3x2 – 1 liên tục và có đạo hàm trên đoạn \(\left[ { - \frac{1}{2};1} \right]\)
Đạo hàm: y’ = 6x2 + 6x
Xét y’ = 0 ⇒ 6x2 + 6x = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ { - \frac{1}{2};1} \right]\\x = - 1 \notin \left[ { - \frac{1}{2};1} \right]\end{array} \right.\)
Ta có: \(y\left( { - \frac{1}{2}} \right) = \frac{{ - 1}}{2}\); y(0) = −1; y(1) = 4
Vậy maxy = 4.
Tập xác định: D = ℝ.
Hàm số y = 2x3 + 3x2 – 1 liên tục và có đạo hàm trên đoạn \(\left[ { - \frac{1}{2};1} \right]\)
Đạo hàm: y’ = 6x2 + 6x
Xét y’ = 0 ⇒ 6x2 + 6x = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ { - \frac{1}{2};1} \right]\\x = - 1 \notin \left[ { - \frac{1}{2};1} \right]\end{array} \right.\)
Ta có: \(y\left( { - \frac{1}{2}} \right) = \frac{{ - 1}}{2}\); y(0) = −1; y(1) = 4
Vậy maxy = 4.
Câu 26:
Anh An là nhân viên bán hàng tại siêu thị điện máy. Anh An kiếm được một khoản hoa hồng 600 nghìn đồng cho mỗi máy giặt và 1,3 triệu dồng cho mỗi tủ lạnh mà anh ấy bán được. Hỏi để nhận được từ 10 triệu đồng trở lên tiền hoa hồng thì anh An cần bán bao nhiêu máy giặt và tủ lạnh.
 Xem đáp án
Xem đáp án
Gọi x và y lần lượt là số máy giặt và tủ lạnh anh bán được (x ; y ∈ ℕ)
Số tiền thu được: 0,6x + 1,3y (triệu đồng)
Theo bài ra, ta có bất phương trình:
0,6x + 1,3y ≥ 10 ⇔ 0,6x + 1,3y – 10 ≥ 0
Vẽ đường thẳng (d): 0,6x + 1,3y – 10 = 0 trên mặt phẳng toạ độ Oxy
Thấy điểm O(0; 0) không thuộc BPT (1) nên miền nghiệm BPT là phần mặt phẳng không chứa O, kể cả đường thẳng (d).
Vậy để nhận được từ 10 triệu đồng trở lên tiền hoa hồng thì anh An cần bán x máy giặt và y tủ lạnh sao cho (x, y) là điểm
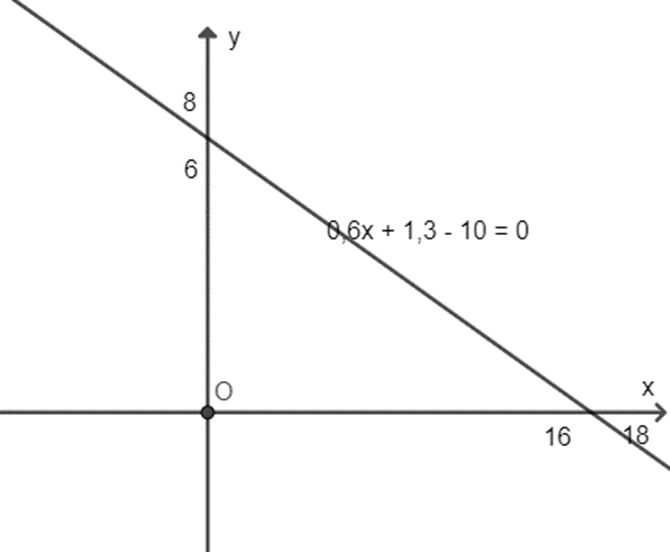
phần mặt phẳng không chứa điểm O, kể cả đường thẳng (d).
Câu 27:
Nhà trường tổ chức cho học sinh khối 5 đi thăm quan. Nễu xếp 40 học sinh một xe thì cần 14 xe ô tô. Hỏi nếu xếp 35 học sinh thì cần bao nhiêu xe? (sức chở của mỗi xe là như nhau)
 Xem đáp án
Xem đáp án
Số học sinh đi tham quan là:
40 ´ 14 = 560 ( học sinh)
Nếu mỗi xe chở 35 học sinh thì cần số xe là:
560 : 35 = 16 (xe)
Đáp số: 16 xe
Câu 28:
Tính a2 + b2 biết a + b = 5 và ab = 1.
 Xem đáp án
Xem đáp án
Ta có:
a2 + b2
= (a + b)2 − 2ab
= 52 – 2.1 = 25 – 2 = 23
Vậy a2 + b2 = 23 khi a + b = 5 và ab = 1.
Câu 29:
Cho 2.(a2 + b2) = (a + b)2. Chứng minh rằng a = b.
 Xem đáp án
Xem đáp án
(a2+ b2) = (a + b)2
⇔ 2a2+ 2b2 = a2 + b2 + 2ab
⇔ 2a2 – a2 + 2b2 – b2 – 2ab = 0
⇔ a2 + b2 – 2ab = 0
⇔ a2 – 2ab + b2 = 0
⇔ (a – b)2 = 0
⇔ a – b = 0
⇔ a = b (đpcm)
Câu 30:
Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chứng minh rằng \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} \).
 Xem đáp án
Xem đáp án
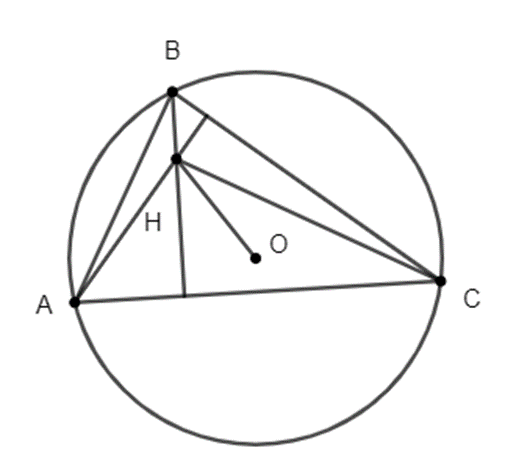
\(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \)
\( \Leftrightarrow \left( {\overrightarrow {HO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {HO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {HO} + \overrightarrow {OC} } \right) = 2\overrightarrow {HO} \)
\( \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} \)
Câu 31:
 Xem đáp án
Xem đáp án
∆ABD nội tiếp đường tròn đường kính AC.
Áp dụng định lý sin trong ∆ABD, ta có:
\(AC = 2R = \frac{{BD}}{{\sin \widehat {BAD}}} = \frac{{a\sqrt 3 }}{{\sin 120^\circ }} = 2a\).
Vậy AC = 2a.
Câu 32:
Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày radio kiểu hai sản xuất trên dây chuyền 2 với công suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu 2 cần 9 linh kiện tiền lãi khi bán một chiếc radio kiểu một là 250 000 đồng tiền lãi thu được khi bán một chiếc Rario kiểu 2 là 180 000 đồng. Hỏi cần sản xuất như thế nào để tiền lãi thu được là nhiều nhất biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900.
 Xem đáp án
Xem đáp án
Gọi số radio kiểu một và kiểu hai mà công ty này sản xuất trong một ngày lần lượt là x, y (x, y ∈ N*,chiếc)
Số tiền lãi công ty thu được trong 1 ngày:
f(x, y) = 250x + 180y (nghìn đồng)
Công suất của dây chuyền 1 là 45 radio/ngày và dây chuyền 2 là 80 radio/ngày
\( \Rightarrow \left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\end{array} \right.\)
Để sản xuất 1 chiếc radio kiểu một cần 12 linh kiện điện tử A và một chiếc radio kiểu hai cần 9 linh kiện này. Số linh kiện này được cung cấp mỗi ngày không quá 900
⇒ 12x + 9y ≤ 900
Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\\12x + 9y \le 900\end{array} \right.\)
Miền của hệ BPT là phần mặt phẳng đậm nhất trong hình, kể cả biên
Khi đó f(x, y) đạt GTLN khi (x, y) là một trong số các điểm A(45; 0); B(45; 40); C(15; 80); D(0; 80).
Thay vào hàm f(x, y) ta có f(x, y) đạt GTLN bằng 18 450 000 đồng khi (x, y) = (45, 40).
Câu 33:
Hình đa giác lồi 6 cạnh có bao nhiêu đường chéo?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D.
Số đường chéo của đa giác lồi n đỉnh là: \(\frac{{x\left( {x - 3} \right)}}{2}\).
Áp dụng công thức ta có số đường chéo của hình lục giác lồi là: \(\frac{{6.\left( {6 - 3} \right)}}{2} = 9\).
Câu 34:
Tìm tập xác định của hàm số \(y = \left\{ \begin{array}{l}\sqrt {3 - x} ,x \in ( - \infty ;0)\\\sqrt {\frac{1}{x}} ,x \in (0; + \infty )\end{array} \right.\).
 Xem đáp án
Xem đáp án
Hàm số \(y = \sqrt {3 - x} \) luôn xác định trên (−\(\infty \); 0).
Hàm số \(y = \sqrt {\frac{1}{x}} \) xác định trên (0; +\(\infty \)).
Điểm x = 0 không nằm trong tập xác định nào, do đó hàm số không xác định tại x = 0.
Vậy tập xác định của hàm số là D = ℝ \ {0}.
Câu 35:
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB = 6a, AC = 7a, AD = 8a. Gọi M, N, P lần lượt là trung điểm của BC, CD, BD. Tính thể tích khối tứ diện AMNP.
 Xem đáp án
Xem đáp án
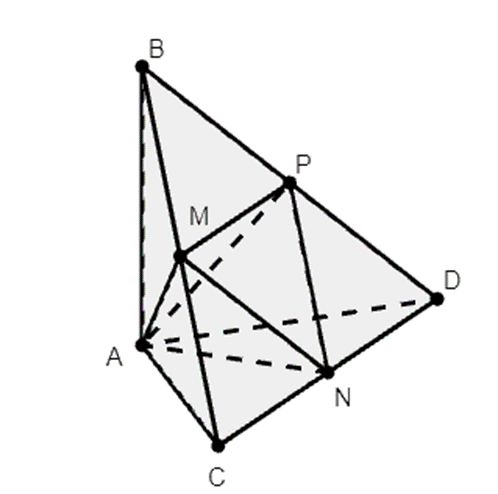
Ta có: \(\frac{{{V_{AMNP}}}}{{{V_{ABCD}}}} = \frac{{d\left( {A,\left( {MNP} \right)} \right).{S_{MNP}}}}{{d\left( {A,\left( {BCD} \right)} \right).{S_{BCD}}}} = \frac{{{S_{MNP}}}}{{{S_{BCD}}}} = \frac{1}{4}\)
\({V_{ABCD}} = \frac{1}{3}.AB.\left( {\frac{1}{2}AC.AD} \right)\)
\( = \frac{1}{6}.6a.7a.8a = 56{a^2}\)
\( \Rightarrow {V_{AMNP}} = \frac{1}{4}.{V_{ABCD}} = \frac{1}{4}.56{a^3} = 14{a^3}\).
Câu 36:
Cho tập hợp X gồm các số tự nhiên có 6 chữ số đôi một khác nhau có dạng \(\overline {abcdef} \). Từ tập hợp X lấy ngẫu nhiên một số. Tính xác suất để số lấy ra là số lẻ và thỏa mãn a < b < c < d < e < f.
 Xem đáp án
Xem đáp án
Số các số có 6 chữ số đôi một khác nhau là:
n(X) = \(A_{10}^6 - A_9^5 = 136\,\,080\).
Gọi A là biến cố số lấy ra lẻ và thỏa mãn a < b < c < d < e < f.
Khi đó f ∈ {7; 9} nên có 2 cách chọn.
+) Nếu f = 7 thì a, b, c, d, e ∈ {1;...;6} (do a ≠ 0 nên b, c, d, e > 0).
Mỗi cách lấy ra một bộ số a, b, c, d, e thì chỉ có duy nhất một cách sắp xếp, do đó số các số trong trường hợp này là số tổ hợp chập 5 của 6 hay \(C_6^5 = 6\) số.
+) Nếu f = 9 thì a, b, c, d, e ∈ {1;...;8} (do a ≠ 0 nên b, c, d, e > 0)
Mỗi cách lấy ra một bộ số a, b, c, d, e thì chỉ có duy nhất một cách sắp xếp, do đó số các số trong trường hợp này là số tổ hợp chập 5 của 8 hay \(C_8^5 = 56\) số.
Do đó n(A) = 6 + 56 = 62.
Xác suất P(A) = \(\frac{{62}}{{136\,\,080}} = \frac{{31}}{{68\,\,040}}\).
Câu 37:
Trung bình mỗi con gà ăn hết 102 g thức ăn trong một ngày. Hỏi trại nuôi gà đó cần bao nhiêu ki-lô-gam thức ăn cho 350 con gà trong 30 ngày?
 Xem đáp án
Xem đáp án
1 ngày trang trại cần số thức ăn là:
102 ´ 350 = 35700 (g) = 35,7 (kg)
Trại nuôi gà đó cần số ki-lô-gam thức ăn cho 350 con gà trong 30 ngày là:
35,7 ´ 30 = 1071 (kg)
Đáp số: 1071 kg.
Câu 38:
Tìm m để 3 đường thẳng y = −5(x + 1), y = mx + 3, y = 3x + m phân biệt và đồng quy.
 Xem đáp án
Xem đáp án
Đặt: d1 : y = −5(x + 1)
d2 : y = mx + 3
d3 : y = 3x + m
Ta có để d2 và d3 cắt nhau thì: m ≠ 3
Để d1 và d2 cắt nhau thì: −5 ≠ m
Gọi A là giao điểm của d1 và d3
Như vậy tọa độ của điểm A thỏa mãn hệ phương trình:
\(\left\{ \begin{array}{l}y = - 5x - 5\\y = 3x + m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + m = - 5x - 5\\y = 3x + m\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{ - m - 5}}{8}\\y = 2.\frac{{ - m - 5}}{8} + m = \frac{{5m - 15}}{8}\end{array} \right.\)
\( \Rightarrow A\left( {\frac{{ - m - 5}}{8};\frac{{5m - 15}}{8}} \right)\)
Để d1, d2, d3 đồng quy thì A ∈ d2
Nên tọa độ của điểm A thỏa mãn phương trình đường thẳng d2
\( \Rightarrow \frac{{5m - 15}}{8} = m.\frac{{ - m - 5}}{8} + 3\)
⇔ 5m – 15 = m(−m – 5) + 24
⇔ m2 + 10m – 39 = 0
\( \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = - 13\end{array} \right.\)
Ta cos m = −13 thoả mãn.
Vậy với m = −13 thỏa mãn yêu cầu bài toán.
Câu 39:
Có 5 tem thư khác nhau và 6 bì thư khác nhau. Từ đó người ta muốn chọn ra 3 tem thư, 3 bì thư và dán 3 tem thư ấy lên 3 bì đã chọn. Hỏi có bao nhiêu cách làm như thế?
 Xem đáp án
Xem đáp án
Số cách chọn 3 tem thư trong 5 tem thư khác nhau là: \(C_5^3\) cách.
Số cách chọn 3 bì thư trong 6 bì thư khác nhau là: \(C_6^3\) cách.
Số cách dán tem thư thứ nhất vào 3 bì thư là: \(C_3^1\) cách.
Số cách dán tem thư thứ hai vào 2 bì thư còn lại là: \(C_2^1\) cách.
Số cách dán tem thư thứ hai vào bì thư cuối cùng là: \(C_1^1\) cách.
Vậy có \(\left( {C_5^3.C_6^3} \right).\left( {C_3^1.C_2^1.C_1^1} \right) = 1200\) cách làm thỏa mãn yêu cầu bài toán.
Câu 40:
Từ các số 0; 1; 2; 7; 8; 9 tạo được bao nhiêu số lẻ có 5 chữ số khác nhau?
 Xem đáp án
Xem đáp án
Gọi \(\overline {abcde} \) là số cần tìm.
Chọn e có 3 cách.
Chọn a ≠ 0 và a ≠ e có 4 cách.
Chọn 3 trong 4 số còn lại sắp vào b, c, d có \(A_4^3\) cách.
Vậy có \(3.4.A_4^3 = 288\) số.
Đáp số: 288 số.
Câu 41:
Có tất cả bao nhiêu số tự nhiên chẵn gồm 5 chữ số khác nhau được thành lập từ các chữ số 1, 2, 3, 4, 5?
 Xem đáp án
Xem đáp án
Gọi số cần tìm có dạng \(\overline {abcde} \).
Vì là số tự nhiên chắn nên e ∈ {2; 4}
Khi đó a có 4 cách chọn
b có 3 cách chọn
c có 2 cách chọn
d có 1 cách chọn
Vậy số số cần tìm là: 2.4.3.2.1 = 48 (số)
Câu 42:
Một mảnh vườn hình vuông cạnh 20 m. Người ta làm một lối đi xung quanh vườn rộng 2 m thuộc đất của vườn. Phần đất còn lại dùng để trồng trọt. Tính diện tích trồng trọt của mảnh vườn.
 Xem đáp án
Xem đáp án
Phần còn lại để trồng trọt là hình vuông có cạnh: 20 − 2 − 2 = 16 (m)
Diện tích trồng trọt của mảnh vườn là: 16 . 16 = 256 (m2)
Vậy diện tích trồng trọt của mảnh vườn là 256 m2.Câu 43:
Rô bốt có hai cái cốc loại 250 ml và 400 ml. Chỉ dùng hai cái cốc đó, làm thế nào để rô bốt lấy được 100 ml nước từ chậu nước.
 Xem đáp án
Xem đáp án
Ta có: 250 ´ 2 – 400 = 100
Vậy đổ 2 cốc 250 ml nước vào cốc 400 ml thì còn dư lại 100 ml trong cốc 250 ml.
