Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 9)
-
1401 lượt thi
-
60 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho hai tập hợp A = {0; 1}, B = {0; 1; 2; 3; 4}. Số tập X thỏa mãn X là con của CAB là bao nhiêu?
 Xem đáp án
Xem đáp án
Ta có CAB = A \ B = ∅.
Vậy số tập X thỏa mãn X là con của CAB là 20 = 1.
Câu 2:
Mua một tá bút chì hết 36 000 đồng. Hỏi mua 39 cái hết bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Đổi: 1 tá bút chì = 12 cây bút chì.
Giá của 1 cây bút chì là: 36 000 : 12 = 3 000 (đồng).
Giá của 39 cây bút chì là: 3 000 × 39 = 117 000 (đồng).
Đáp số: 117 000 đồng.
Câu 3:
Chứng minh nếu n2 là số chẵn thì n cũng là số chẵn.
 Xem đáp án
Xem đáp án
Giả sử n2 là số chẵn nhưng n là số lẻ.
Suy ra n = 2k + 1, với k ∈ ℕ.
Do đó n2 = 4k2 + 4k + 1, với k ∈ ℕ.
Mà 4k2 + 4k + 1 là số lẻ.
Suy ra n2 là số lẻ (mâu thuẫn với đề bài).
Vậy n2 là số chẵn thì n cũng là số chẵn.
Câu 4:
Người ta phơi 450 kg hạt tươi thì được hạt khô. Biết tỉ lệ nước trong hạt tươi là 20%, tỉ lệ nước trong hạt khô là 10%. Tính khối lượng hạt khô.
 Xem đáp án
Xem đáp án
Khối lượng thuần hạt trong hạt tươi chiếm: 100% – 20% = 80% (so với hạt tươi).
Khối lượng thuần hạt là: 450 × 80% = 360 (kg).
Khối lượng thuần hạt trong hạt khô chiếm: 100% – 10% = 90% (so với hạt khô).
Khối lượng hạt khô là: 360 : 90% = 400 (kg).
Đáp số: 400 kg.
Câu 5:
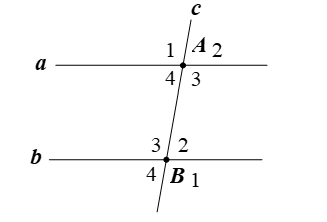
Cho hình vẽ. Biết , . Chứng tỏ a // b.
 Xem đáp án
Xem đáp án
Ta có: .
Mà cặp góc này ở vị trí trong cùng phía.
Vậy a // b.
Câu 6:
Tìm số tự nhiên n, biết 2n chia hết cho 3n – 1.
 Xem đáp án
Xem đáp án
Theo đề, ta có: 2n ⋮ (3n – 1).
⇒ 3.2n ⋮ (3n – 1).
⇒ 6n ⋮ (3n – 1).
⇒ (3n – 1 + 3n – 1 + 2) ⋮ (3n – 1).
Vì (3n – 1) ⋮ (3n – 1) nên 2 ⋮ (3n – 1).
Ư(2) = {1; 2}.
• Với 3n – 1 = 1, ta có: 3n = 2. Suy ra .
• Với 3n – 1 = 2, ta có: 3n = 3. Suy ra n = 1 ∈ ℕ.
Thử lại: n = 1 ta có 2n = 2 và 3n – 1 = 2 nên 2n chia hết cho 3n – 1.
Vậy n = 1 thỏa mãn yêu cầu bài toán.
Câu 7:
Cho tam giác ABC biết độ dài ba đường trung tuyến lần lượt bằng 15, 18, 27.
a) Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
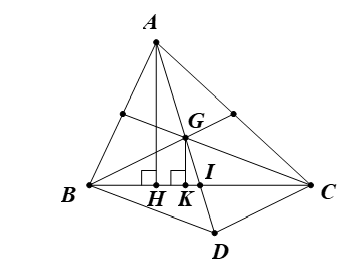
a) Gọi I là trung điểm BC và G là trọng tâm của tam giác ABC.
Suy ra .
Kẻ AH ⊥ BC và GK ⊥ BC (H, K ∈ BC).
Suy ra AH // GK.
Áp dụng định lí Thales, ta được: .
Khi đó .
Suy ra SABC = 3SGBC.
Lấy D là điểm đối xứng với G qua I.
Suy ra I là trung điểm của GD.
Khi đó tứ giác BGCD là hình bình hành.
Suy ra .
Do đó SABC = 3SBGD.
Giả sử ma = 15, mb = 18, mc = 27.
Suy ra
Ta có I là trung điểm của GD.
Suy ra .
Nửa chu vi của tam giác BGD là: .
Diện tích của tam giác BGD là: .
Suy ra .
Vậy diện tích tam giác ABC bằng .
Câu 8:
b) Tính độ dài các cạnh của tam giác ABC.
 Xem đáp án
Xem đáp án
b) Ta có ma = 15, mb = 18, mc = 27.
.
Vậy
Câu 9:
Tính nhanh: , với n ∈ ℕ.
 Xem đáp án
Xem đáp án
Ta có , với n ∈ ℕ.
, với n ∈ ℕ.
, với n ∈ ℕ.
Vậy , với n ∈ ℕ.
Câu 10:
Bình mua 5 cái bút chì và 2 quyển vở hết 20 000 đồng, mua 5 cái bút chì và 4 quyển vở như vậy hết 30 000 đồng. Hỏi giá tiền 1 cái bút chì là bao nhiêu?
 Xem đáp án
Xem đáp án
Số vở mua lần 2 nhiều hơn lần 1 là: 4 – 2 = 2 (quyển vở).
Số tiền mua 2 quyển vở là: 30 000 – 20 000 = 10 000 (đồng).
Số tiền mua 5 cái bút chì là: 20 000 – 10 000 = 10 000 (đồng).
Giá tiền 1 cái bút chì là: 10 000 : 5 = 2 000 (đồng).
Đáp số: 2 000 đồng.
Câu 11:
Tìm 2 số, biết số lớn bằng số bé và nếu lấy số lớn trừ số bé rồi cộng với hiệu của chúng thì được 64.
 Xem đáp án
Xem đáp án
Hiệu của số lớn và số bé là: 64 : 2 = 32.
Hiệu số phần bằng nhau là: 7 – 5 = 2 (phần).
Số lớn là: 32 : 2 × 7 = 112.
Số bé là: 32 : 2 × 5 = 80.
Đáp số: Số lớn: 112;
Số bé: 80.
Câu 12:
Cho hình bình hành ABCD. Trên các cạnh AB, CD lần lượt lấy các điểm E, F sao cho AE = CF. Chứng minh rằng:
a) Tứ giác AECF là hình bình hành.
 Xem đáp án
Xem đáp án
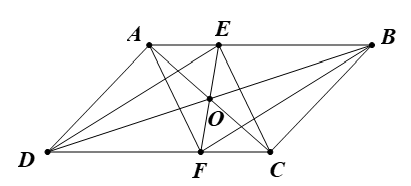
a) Tứ giác AECF, có: AE = CF (giả thiết) và AE // CF (do ABCD là hình bình hành).
Suy ra tứ giác AECF là hình bình hành.
Câu 13:
b) BF // ED.
 Xem đáp án
Xem đáp án
b) Ta có AB = CD (do ABCD là hình bình hành) và AE = CF (giả thiết).
Suy ra AB – AE = CD – CF.
Do đó BE = DF.
Mà BE // FD (do ABCD là hình bình hành).
Vì vậy tứ giác BEDF là hình bình hành.
Vậy BF // ED.
Câu 14:
c) Các đường thẳng AC, EF, BD đồng quy.
 Xem đáp án
Xem đáp án
c) Gọi O là giao điểm của AC và BD.
Suy ra O là trung điểm của AC và BD.
Ta có tứ giác AECF là hình bình hành (kết quả câu a).
Mà O là trung điểm của AC.
Do đó O cũng là trung điểm của EF.
Vậy ba đường thẳng AC, BD, EF đồng quy tại O.
Câu 15:
Cho tam giác ABC, D là một điểm trên cạnh BC. Gọi E và F theo thứ tự là điểm đối xứng của điểm D qua AB và AC.
a) Chứng minh AE = AF.
 Xem đáp án
Xem đáp án
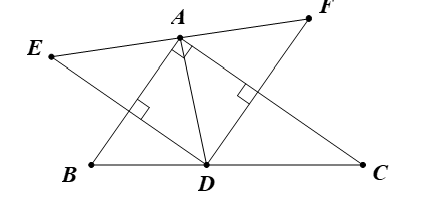
a) Ta có E là điểm đối xứng của D qua AB.
Suy ra AB là đường trung trực của đoạn DE.
Do đó AE = AD (1)
Chứng minh tương tự, ta được: AD = AF (2)
Từ (1), (2), suy ra AE = AF.
Câu 16:
b) Tam giác ABC phải có thêm điều kiện gì để điểm E đối xứng với điểm F qua điểm A?
 Xem đáp án
Xem đáp án
b) Để điểm E đối xứng với điểm F qua điểm A thì cần thỏa 2 điều kiện:
⦁ AE = AF (đã chứng minh ở câu a).
⦁ Ba điểm E, A, F thẳng hàng, tức là .
Tam giác AED cân tại A có AB là đường trung trực.
Suy ra AB cũng là đường phân giác của tam giác AED.
Do đó .
Chứng minh tương tự, ta được .
Khi đó ta có .
Mà .
Suy ra .
Khi đó tam giác ABC vuông tại A.
Vậy tam giác ABC vuông tại A thì điểm E đối xứng với điểm F qua điểm A.
Câu 18:
Một cửa hàng bán vải, buổi sáng bán được tấm vải, buổi chiều bán được số vải còn lại và tấm vải còn 20 m. Hỏi tấm vải dài bao nhiêu mét?
 Xem đáp án
Xem đáp án
Số vải còn lại sau khi bán buổi sáng là: (tấm vải).
Số vải buổi chiều bán được là: (tấm vải).
Số vải còn lại sau khi bán xong 2 buổi là: (tấm vải).
Tấm vải dài số mét là: (m).
Đáp số: 44 m.
Câu 19:
Một khu đất hình chữ nhật có chu vi 150 m, chiều dài hơn chiều rộng 5 m. Hỏi diện tích khu đất là bao nhiêu đề-ca-mét vuông?
 Xem đáp án
Xem đáp án
Nửa chu vi khu đất là: 150 : 2 = 75 (m).
Chiều dài khu đất là: (75 + 5) : 2 = 40 (m).
Chiều rộng khu đất là: (75 – 5) : 2 = 35 (m).
Diện tích khu đất là: 40 × 35 = 1400 (m2).
Đổi: 1400 m2 = 14 dam2.
Đáp số: 14 dam2.
Câu 20:
Tìm các bội chung có ba chữ số của 63; 35 và 105.
 Xem đáp án
Xem đáp án
Ta có 63 = 32.7; 35 = 5.7 và 105 = 3.5.7.
Suy ra BCNN(63, 35, 105) = 32.5.7 = 315.
Suy ra BC(63, 35, 105) = B(315) = {0; 315; 630; 945; 1260; ...}.
Vậy các bội chung có ba chữ số của 63; 35 và 105 là: 315; 630 và 945.
Câu 21:
Tính thỏa mãn a3 + b3 + c3 = 3abc.
 Xem đáp án
Xem đáp án
Đặt .
Ta có: (a + b + c)3 = a3 + b3 + c3 + 6abc + 3(a2b + ab2 + b2c + bc2 + c2a + a2c).
⇔ (a + b + c)3 = (3abc + 3a2b + 3ab2) + (3abc + 3b2c + 3bc2) + (3abc + 3c2a + 3a2c).
⇔ (a + b + c)3 = 3ab(a + b + c) + 3bc(a + b + c) + 3ac(a + b + c).
⇔ (a + b + c)3 = 3(ab + bc + ca)(a + b + c).
⇔ (a + b + c).[(a + b + c)2 – 3(ab + bc + ca)] = 0.
Từ (1), ta có: .
Từ (2), ta có: (a + b + c)2 = 3(ab + bc + ca).
⇔ a2 + b2 + c2 + 2ab + 2bc + 2ca = 3ab + 3bc + 3ca.
⇔ a2 + b2 + c2 = ab + bc + ca.
⇔ (a2 – 2ab + b2) + (b2 – 2bc + c2) + (c2 – 2ca + a2) = 0.
⇔ (a – b)2 + (b – c)2 + (c – a)2 = 0.
.
Với a = b = c, ta có: .
Vậy .
Câu 22:
Tổng của năm số là 600. Tìm số thứ năm, biết rằng số này bằng số trung bình cộng của bốn số còn lại.
 Xem đáp án
Xem đáp án
Vì số thứ năm bằng trung bình cộng của bốn số còn lại nên 4 lần số thứ năm bằng tổng của bốn số còn lại.
Số thứ 5 là: 600 : (4 + 1) × 1 = 120.
Đáp số: 120.
Câu 23:
 Xem đáp án
Xem đáp án
Đặt .
Ta có x là số nguyên dương. Suy ra x ≥ 1.
⇒ x + 1 ≥ 2.
.
.
.
⇒ A ≤ 4.
Dấu “=” xảy ra ⇔ x = 1.
Vậy khi x = 1 thì biểu thức lớn nhất.
Câu 24:
Cho các số nguyên x, y thỏa mãn x2006 + y2006 = x2007 + y2007 = x2008 + y2008. Tính tổng S = x2009 + y2009.
 Xem đáp án
Xem đáp án
Nếu x = y = 1 thì 12006 + 12006 = 12007 + 12007 = 12008 + 12008 = 2 (thỏa mãn).
Nếu x = y = –1 thì (–1)2006 + (–1)2006 = 2 và (–1)2007 + (–1)2007 = –2.
Suy ra (–1)2006 + (–1)2006 ≠ (–1)2007 + (–1)2007.
Nếu x = –1, y = 1 thì (–1)2006 + 12006 ≠ (–1)2007 + 12007.
Nếu x = 1, y = –1 thì 12006 + (–1)2006 ≠ 12007 + (–1)2007.
Nếu x > 1, –1 < y < 1 hoặc x < –1, –1 < y < 1 thì
Suy ra x2006 + y2006 < x2008 + y2008.
Nếu x > 1, y < –1 hoặc x > 1, y > 1 hoặc x < –1, y < –1 hoặc x < –1, y > 1 thì .
Suy ra x2008 + y2008 > x2006 + y2006.
Nếu –1 < x < 1, y > 1 hoặc –1 < x < 1, y < –1 thì
Suy ra x2006 + y2006 < x2008 + y2008.
Nếu –1 < x, y < 1 thì .
Suy ra x2008 + y2008 < x2006 + y2006.
Vì vậy x = 1 là giá trị duy nhất thỏa mãn x2006 + y2006 = x2007 + y2007 = x2008 + y2008.
Vậy S = x2009 + y2009 = 12009 + 12009 = 1 + 1 = 2.
Câu 25:
 Xem đáp án
Xem đáp án
Ta có x4 + 2009x2 + 2008x + 2009
= (x4 – x) + (2009x2 + 2009x + 2009)
= x(x3 – 1) + 2009(x2 + x + 1)
= x(x – 1)(x2 + x + 1) + 2009(x2 + x + 1)
= (x2 – x)(x2 + x + 1) + 2009(x2 + x + 1)
= (x2 + x + 1)(x2 – x + 2009).
Câu 26:
Cho đường tròn (O) và dây AB không là đường kính. Gọi M là trung điểm của AB. Qua M vẽ dây CD không trùng với AB. Chứng minh:
a) M không là trung điểm của CD.
 Xem đáp án
Xem đáp án
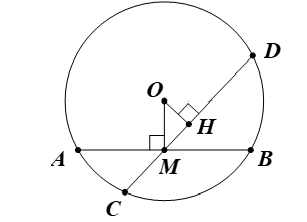
a) Giả sử M là trung điểm của CD.
Suy ra OM ⊥ CD.
Mà OM ⊥ AB (vì M là trung điểm AB).
Do đó CD trùng với AB (mâu thuẫn với giả thiết).
Vậy M không là trung điểm của CD.
Câu 27:
Chứng minh:
b) AB < CD.
 Xem đáp án
Xem đáp án
b) Kẻ OH ⊥ CD.
Tam giác OHM vuông tại H có OM là cạnh huyền, OH là cạnh góc vuông.
Suy ra OH < OM.
Vậy CD > AB (dây nào gần tâm hơn thì dây đó lớn hơn).
Câu 28:
 Xem đáp án
Xem đáp án
Ta có (4n – 17) ⋮ (2n + 5).
⇒ (4n + 10) – 27 ⋮ (2n + 5).
⇒ 2(2n + 5) – 27 ⋮ (2n + 5).
Mà 2(2n + 5) ⋮ (2n + 5).
Do đó 27 ⋮ (2n + 5).
Ta có Ư(27) ∈ {1; 3; 9; 27}.
Ta có bảng sau:
|
2n + 5 |
1 |
3 |
9 |
27 |
|
n |
–2 |
–1 |
2 |
11 |
Mà n ∈ ℕ.
Suy ra n ∈ {2; 11}.
Vậy n ∈ {2; 11} thỏa mãn yêu cầu bài toán.
Câu 29:
Thực hiện phép tính: 53 . 75 : 35.
 Xem đáp án
Xem đáp án
Ta có 53 . 75 : 35
= 53 . 75 : (5 . 7)
= 53 – 1 . 75 – 1
= 52 . 74
= 25 . 2401
= 60 025.
Câu 30:
Có hai xe ô tô, mỗi xe chở 4200 kg gạo và 3 xe ô tô, mỗi xe chở 3600 kg gạo. Trung bình mỗi xe chở số ki-lô-gam gạo là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Trung bình mỗi xe chở số ki-lô-gam gạo là: (4200 × 2 + 3600 × 3) : 5 = 3840 (kg).
Đáp số: 3840 kg.
Vậy ta chọn phương án C.
Câu 31:
Tìm các số nguyên x, y sao cho xy chia hết cho (x + y).
 Xem đáp án
Xem đáp án
Xét phương trình xy = k(x + y), với x, y, k là các số nguyên.
⇔ (x – k)(y – k) = k2 (*)
Suy ra x – k chia hết cho k2.
Đặt x – k = d (d chia hết cho k2).
Khi đó x = d + k.
Thế x = d + k vào (*), ta được: d(y – k) = k2.
.
Vậy tất cả các cặp số (x; y) cần tìm có dạng , với d, k là các số nguyên và d chia hết cho k2.
Câu 32:
Khai triển nhị thức (a + b)n (công thức nhị thức Newton).
 Xem đáp án
Xem đáp án
Khi khai triển nhị thức (a + b)n, ta được công thức:
.
.
Câu 33:
Cho tứ giác ABCD có AB = BC, AD < CD. BD là phân giác của . Chứng minh .
 Xem đáp án
Xem đáp án
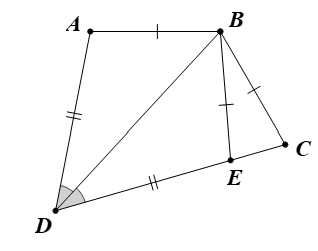
Trên cạnh CD, lấy điểm E sao cho DE = DA.
Xét ∆ABD và ∆EBD, có:
BD là cạnh chung;
DA = DE (giả thiết);
(do BD là phân giác của ).
Do đó ∆ABD = ∆EBD (c.g.c).
Suy ra AB = EB và (cặp cạnh và cặp góc tương ứng).
Mà AB = BC (giả thiết)
Do đó EB = BC.
Vì vậy tam giác BCE cân tại B.
Suy ra .
Ta có (cặp góc kề bù).
Vậy .
Câu 34:
Năm ngoái, tổng số dân của hai tỉnh A và B là 4 triệu người. Năm nay, dân tỉnh A tăng 1,2%, còn số dân tỉnh B tăng 1,1%. Tổng số dân của 2 tỉnh năm nay là 4 045 000 người. Tính số dân của hai tỉnh trong năm nay.
 Xem đáp án
Xem đáp án
Gọi số dân của tỉnh A và tỉnh B năm ngoái lần lượt là x, y (người; x , y < 4 000 000; x, y ∈ ℕ*).
Theo đề, ta có hệ phương trình: .
Số dân tỉnh A năm nay là: 1 000 000.101,2% = 1 012 000 (người).
Số dân tỉnh B năm nay là: 3 000 000.101,1% = 3 033 000 (người).
Vậy số dân tỉnh A và tỉnh B năm nay lần lượt là 1 012 000 người và 3 033 000 người.
Câu 35:
Năm ngoái, tổng số dân của hai tỉnh A và B là 4 triệu. Năm nay, dân số của tỉnh A tăng thêm 1,1%, còn dân số của tỉnh B tăng thêm 1,2%. Tuy vậy số dân của tỉnh A năm nay vẫn nhiều hơn tỉnh B là 807 200 người. Tính số dân năm ngoái của mỗi tỉnh.
 Xem đáp án
Xem đáp án
Gọi x là số dân năm ngoái của tỉnh A (0 < x < 4; x ∈ ℕ*; triệu người).
Suy ra số dân năm ngoái của tình B là: 4 – x (triệu người).
Năm nay dân số của tỉnh A tăng 1,1% nên số dân của tỉnh A năm nay là: x + 1,1%.x = 1,011.x.
Năm nay dân số của tỉnh B tăng 1,2% nên số dân của tỉnh B năm nay là: (4 – x) + 1,2%.(4 – x) = 1,012.(4 – x).
Vì số dân tỉnh A năm nay hơn tỉnh B là 807 200 người = 0,8072 triệu người nên ta có phương trình: 1,011.x – 1,012.(4 – x) = 0,8072.
⇔ 1,011.x – 4,048 + 1,012.x = 0,8072.
⇔ 2,023.x = 4,8552.
⇔ x = 2,4 (nhận).
Vậy dân số của tỉnh A năm ngoái là 2,4 triệu người; dân số tỉnh B năm ngoái là 4 – 2,4 = 1,6 triệu người.
Câu 36:
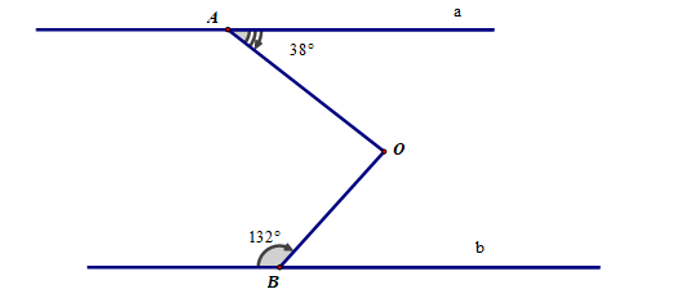
Cho hình vẽ dưới, biết a // b. Tính số đo .
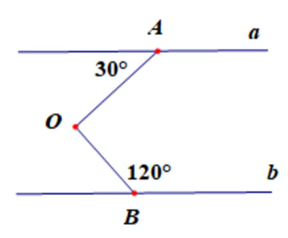
 Xem đáp án
Xem đáp án
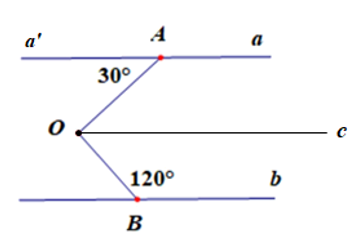
Vẽ tia Oc // a. Suy ra Oc // b.
Ta có a // Oc. Suy ra (cặp góc so le trong).
Lại có b // Oc. Suy ra (cặp góc trong cùng phía).
Do đó .
Vậy .
Câu 37:
 Xem đáp án
Xem đáp án
Vẽ tia Om // a. Suy ra Om // b.
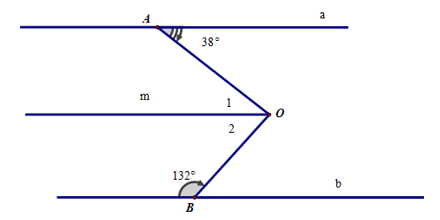
Ta có Om // a. Suy ra (cặp góc so le trong).
Lại có Om // b. Suy ra (cặp góc trong cùng phía).
Do đó .
Vậy .
Câu 39:
Cho hai biểu thức A = 3 + 32 + 33 + 34 + ... + 3100 và B = 3101 – 1. Chứng minh rằng A < B.
 Xem đáp án
Xem đáp án
Ta có A = 3 + 32 + 33 + 34 + ... + 3100.
Suy ra 3A = 32 + 33 + 34 + 35 + ... + 3101.
Do đó 3A – A = (32 – 32) + (33 – 33) + (34 – 34) + ... + (3100 – 3100) + 3101 – 3.
Vì vậy 2A = 3101 – 3.
Ta thấy 3101 – 3 < 3101 – 1.
Suy ra 2A < B.
Vậy A < B.
Câu 40:
Có 3 thùng dầu đựng tổng cộng 84 lít, biết số dầu của thùng thứ nhất bằng số dầu thùng thứ hai, số dầu thùng thứ ba bằng tổng số dầu của thùng thứ nhất và thùng thứ hai. Hỏi mỗi thùng có bao nhiêu lít dầu?
 Xem đáp án
Xem đáp án
Tổng số phần bằng nhau của thùng thứ ba và tổng số dầu thùng thứ nhất, thứ hai là:
3 + 4 = 7 (phần).
Số dầu ở thùng thứ ba là: 84 : 7 × 3 = 36 (lít).
Tổng số dầu của thùng thứ nhất và thùng thứ hai là: 84 : 7 × 4 = 48 (lít).
Tổng số phần bằng nhau của thùng thứ nhất và thùng thứ hai là:
3 + 5 = 8 (phần).
Số dầu ở thùng thứ nhất là: 48 : 8 × 3 = 18 (lít).
Số dầu ở thùng thứ hai là: 48 : 8 × 5 = 30 (lít).
Đáp số: 18 lít; 30 lít; 36 lít.
Câu 41:
 Xem đáp án
Xem đáp án
Ta có y ∈ ℕ và 0 ≤ y ≤ 9.
Ta có .
.
Vì 9 × 14 × 43 × 44 × 15 × A chia hết cho 9 nên cũng chia hết cho 9.
⇒ 6 + 0 + 7 + y + 9 + 9 + 6 + 0 = 37 + y chia hết cho 9.
⇒ 4 × 9 + 1 + y chia hết cho 9.
Mà 4 × 9 chia hết cho 9.
⇒ 1 + y chia hết cho 9.
Vậy y = 8 thỏa yêu cầu bài toán.
Câu 42:
Thực hiện phép tính: 55 . 75 : 35.
 Xem đáp án
Xem đáp án
Ta có 55 . 75 : 35
= (5 . 7)5 : 35
= 355 : 35
= 355 – 1
= 354
= 1 500 625.
3781. cho ba số thập phânCâu 43:
Cho ba số thập phân. Nếu chuyển dấu phẩy của số thứ nhất về bên trái một chữ số ta được số thứ hai. Nếu chuyển dấu phẩy của số thứ nhất về bên phải một chữ số ta được số thứ ba. Tìm ba số đó biết tổng của ba số là 2118,99.
 Xem đáp án
Xem đáp án
Nếu chuyển dấu phẩy của số thứ nhất về bên trái một chữ số ta được số thứ hai.
Suy ra số thứ nhất gấp 10 lần số thứ hai.
Nếu chuyển dấu phẩy của số thứ nhất về bên phải một chữ số ta được số thứ ba.
Suy ra số thứ ba gấp 10 lần số thứ nhất.
Do đó số thứ ba gấp 100 lần số thứ hai.
Số thứ hai là: 2118,99 : (1 + 100 + 10) = 19,09.
Số thứ nhất là: 19,09 × 10 = 190,9.
Số thứ ba là: 19,09 × 100 = 1909.
Đáp số: Số thứ nhất: 190,9;
Số thứ hai: 19,09;
Số thứ ba: 1909.
Câu 44:
Cho ba số thập phân. Nếu chuyển dấu phẩy của số thứ nhất về bên trái một chữ số ta được số thứ hai. Nếu chuyển dấu phẩy của số thứ nhất về bên phải một chữ số ta được số thứ ba. Tổng của ba số là 150,627. Tìm ba số đó.
 Xem đáp án
Xem đáp án
Nếu chuyển dấu phẩy của số thứ nhất về bên trái một chữ số ta được số thứ hai.
Suy ra số thứ nhất gấp 10 lần số thứ hai.
Nếu chuyển dấu phẩy của số thứ nhất về bên phải một chữ số ta được số thứ ba.
Suy ra số thứ ba gấp 10 lần số thứ nhất.
Do đó số thứ ba gấp 100 lần số thứ hai.
Số thứ hai là: 150,627 : (1 + 100 + 10) = 1,357.
Số thứ nhất là: 1,357 × 10 = 13,57.
Số thứ ba là: 1,357 × 100 = 135,7.
Đáp số: Số thứ nhất: 13,57;
Số thứ hai: 1,357;
Số thứ ba: 135,7.
Câu 45:
Cho biểu thức . Chứng minh biểu thức A có giá trị không phải là số nguyên.
 Xem đáp án
Xem đáp án
Ta có
.
Đặt
.
Mà .
Suy ra .
.
.
.
Mà B > 0 nên 0 < B < 1.
Do đó B không phải là số nguyên.
Vậy A = 49 + B không phải là số nguyên (điều phải chứng minh).
Câu 46:
Cho tam giác ABC có . Kẻ BH vuông góc với AC tại H và CK vuông góc với AB tại K.
a) Chứng minh KH = BC.cosA.
 Xem đáp án
Xem đáp án
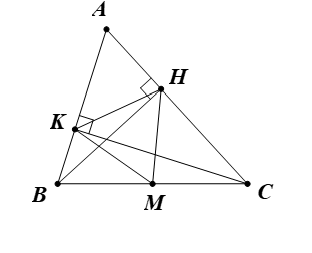
a) Xét ∆AKC và ∆AHB, có:
chung;
.
Do đó (g.g).
Suy ra .
Do đó .
Xét ∆AKH và ∆ACB, có:
chung;
(chứng minh trên).
Do đó (c.g.c).
Suy ra .
Vậy KH = BC.cosA.
Câu 47:
b) Gọi M là trung điểm của BC. Chứng minh tam giác MKH là tam giác đều.
 Xem đáp án
Xem đáp án
b) Tam giác BCK vuông tại K có M là trung điểm BC.
Suy ra (1)
Chứng minh tương tự, ta được (2)
Từ (1), (2), suy ra (*)
Mà KH = BC.cosA (kết quả câu a).
Do đó (**)
Từ (*), (**), suy ra KM = HM = KH.
Vậy tam giác MKH là tam giác đều.
Câu 48:
Cho tam giác ABC thỏa mãn a3 = b3 + c3. Chứng minh rằng tam giác ABC có ba góc nhọn.
 Xem đáp án
Xem đáp án
Ta có a3 = b3 + c3. Suy ra a là cạnh lớn nhất.
Do đó là góc lớn nhất.
Ta chứng minh nhọn là đủ. Thật vậy, ta có:
a3 = b3 + c3 = b.b2 + c.c2 < a.b2 + a.c2 = a(b2 + c2).
Suy ra a2 < b2 + c2.
Do đó b2 + c2 – a2 > 0.
Vì vậy .
Suy ra cosA > 0.
Do đó .
Vậy tam giác ABC có ba góc nhọn.
Câu 49:
Tìm giá trị nhỏ nhất của biểu thức B = (x – 15)2 + 2021.
 Xem đáp án
Xem đáp án
Ta có (x – 15)2 ≥ 0, ∀x ∈ ℝ.
⇔ (x – 15)2 + 2021 ≥ 0, ∀x ∈ ℝ.
⇔ B ≥ 2021, ∀x ∈ ℝ.
Dấu “=” xảy ra ⇔ x = 15.
Vậy giá trị nhỏ nhất của biểu thức B bằng 2021 khi và chỉ khi x = 15.
Câu 50:
 Xem đáp án
Xem đáp án
Mỗi phút 2 vòi chảy được số lít nước là: 120 : 15 = 8 (lít).
Mỗi phút mỗi vòi chảy được số lít nước là: 8 : 2 = 4 (lít).
Mỗi phút 3 vòi chảy được số lít nước là: 4 × 3 = 12 (lít).
16 phút 3 vòi chảy được số lít nước là: 12 × 16 = 192 (lít).
Đáp số: 192 lít.
Câu 51:
Một hình chữ nhật có chu vi là 160 cm. Tính chiều dài của hình chữ nhật, biết 2 lần chiều dài bằng 3 lần chiều rộng.
 Xem đáp án
Xem đáp án
Nửa chu vi hình chữ nhật là: 160 : 2 = 80 (cm).
Ta có 2 lần chiều dài bằng 3 lần chiều rộng.
Suy ra chiều dài bằng chiều rộng.
Chiều dài hình chữ nhật là: 80 : (3 + 2) × 3 = 48 (cm).
Đáp số: 48 cm.
Câu 52:
Trong lớp 10A có 15 học sinh giỏi môn Toán, 14 học sinh giỏi môn Văn và 12 học sinh giỏi môn Anh. Biết rằng có 8 học sinh giỏi hai môn Văn và Toán, có 5 học sinh giỏi hai môn Văn và Anh, có 7 học sinh giỏi hai môn Toán và Anh, trong đó chỉ có 11 học sinh giỏi cả 2 môn. Hỏi có bao nhiêu học sinh của lớp:
a) Giỏi cả 3 môn Toán, Văn, Anh.
 Xem đáp án
Xem đáp án
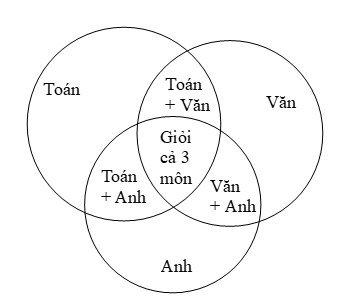
a) Từ biểu đồ trên, ta thấy: tổng số học sinh giỏi 2 trong 3 môn (Toán và Văn; Văn và Anh; Toán và Anh) – 3 lần số học sinh giỏi cả 3 môn (Toán, Văn, Anh) = Số học sinh chỉ giỏi 2 trong 3 môn.
Vậy số học sinh giỏi cả 3 môn là: (8 + 5 + 7 – 11) : 3 = 3 (học sinh).
Câu 53:
b) Giỏi đúng 1 môn Văn, Toán hoặc Anh.
 Xem đáp án
Xem đáp án
b) Số học sinh chỉ giỏi Toán là: 15 – (8 + 7 – 3) = 3 (học sinh).
Số học sinh chỉ giỏi Văn là: 14 – (8 + 5 – 3) = 4 (học sinh).
Số học sinh chỉ giỏi Anh là: 12 – (7 + 5 – 3) = 3 (học sinh).
Vậy số học sinh chỉ giỏi một trong ba môn Toán, Văn, Anh lần lượt là 3 học sinh; 4 học sinh; 3 học sinh.
Câu 54:
Lúc đầu thùng thứ nhất có nhiều hơn thùng thứ hai là 5 lít dầu. Người ta đã bán đi 10 lít ở thùng thứ hai và 5 lít ở thùng thứ nhất. Lúc này số dầu ở thùng thứ hai bằng số dầu ở thùng thứ nhất. Hỏi lúc đầu mỗi thùng có bao nhiêu lít dầu?
 Xem đáp án
Xem đáp án
Sau khi đã bán đi 10 lít ở thùng thứ hai và 5 lít ở thùng thứ nhất thì số lít dầu thùng thứ nhất có nhiều hơn thùng thứ hai là: 5 + (10 – 5) = 10 (lít dầu).
Hiệu số phần bằng nhau là: 5 – 3 = 2 (phần).
Lúc đầu, thùng thứ nhất có số lít dầu là: 10 : 2 × 5 + 5 = 30 (lít dầu).
Lúc đầu, thùng thứ hai có số lít dầu là: 30 – 5 = 25 (lít dầu).
Đáp số: Thùng thứ nhất: 30 lít dầu;
Thùng thứ hai: 25 lít dầu.
Câu 55:
Một cửa hàng bán vải, buổi sáng bán được tấm vải, buổi chiều bán được số vải còn lại và tấm vải còn 20 m. Hỏi tấm vải dài bao nhiêu mét?
 Xem đáp án
Xem đáp án
Số vải còn lại sau khi bán buổi sáng là: (tấm vải).
Số vải buổi chiều bán được là: (tấm vải).
Số vải còn lại sau khi bán cả hai buổi là: (tấm vải).
Tấm vải dài là: (m).
Đáp số: 44 m.
Câu 56:
Một hình chữ nhật có chiều dài là 360 m, chiều rộng bằng chiều dài. Tính diện tích hình chữ nhật đó với đơn vị là ha.
 Xem đáp án
Xem đáp án
Chiều rộng của hình chữ nhật là: (m).
Diện tích hình chữ nhật là: 360 × 240 = 86 400 (m2).
Đổi: 86 400 m2 = 864 ha.
Đáp số: 864 ha.
Câu 57:
Một hình chữ nhật có chiều dài gấp đôi chiều rộng. Nếu thêm vào chiều dài 15 m và chiều rộng 20 m thì chiều dài gấp rưỡi chiều rộng. Tính diện tích hình chữ nhật ban đầu?
 Xem đáp án
Xem đáp án
Gọi độ dài chiều rộng ban đầu là a (m).
Suy ra độ dài chiều dài ban đầu là 2 × a (m).
Nếu thêm vào chiều dài 15 m và chiều rộng 20 m thì chiều dài gấp rưỡi chiều rộng.
Suy ra 2 × a + 15 = 1,5 × (a + 20).
2 × a + 15 = 1,5 × a + 30.
2 × a – 1,5 × a = 30 – 15.
0,5 × a = 15.
a = 15 : 0,5 = 30 (m).
Chiều dài ban đầu là: 2 × 30 = 60 (m).
Diện tích hình chữ nhật ban đầu là: 60 × 30 = 1800 (m2).
Đáp số: 1800 m2.
Câu 58:
Một nông trại nuôi một đàn gia súc gồm 3 loại: trâu, bò, dê. Số trâu bằng số gia súc, số bò là 52 con và số dê bằng tổng số trâu và bò. Hỏi đàn gia súc có bao nhiêu con?
 Xem đáp án
Xem đáp án
Vì số dê bằng tổng số trâu và bò nên số dê bằng tổng số trâu, bò, dê.
Số bò chiếm: (số gia súc).
Đàn gia súc có số con là: (con).
Đáp số: 180 con.
Câu 59:
Một tổ 15 công nhân dự định lắp xong một cỗ máy trong vòng 20 ngày, mỗi ngày làm việc 8 giờ. Nếu thêm 5 người nữa và mỗi ngày làm việc 10 giờ thì sẽ lắp xong cỗ máy đó trong mấy ngày?
 Xem đáp án
Xem đáp án
Thời gian để một người hoàn thành cỗ máy là: 15 × 20 × 8 = 2400 (giờ).
Nếu có thêm 5 người, thời gian để tổ công nhân lắp xong cỗ máy là:
2400 : (15 + 5) = 120 (giờ).
Nếu mỗi ngày làm việc 10 giờ thì thời gian lắp xong cỗ máy đó là:
120 : 10 = 12 (ngày).
Đáp số: 12 ngày.
Câu 60:
Một xe đạp đi từ A đến B nửa quãng đường đầu, xe đi với vận tốc 20 km/h nửa còn lại đi với vận tốc 30 km/h. Hỏi vận tốc trung bình của xe đạp trên cả quãng đường là bao nhiêu?
 Xem đáp án
Xem đáp án
Thời gian đi nửa quãng đường đầu là:
(giờ)
Thời gian đi nửa quãng sau là:
(giờ)
Vận tốc trung bình của xe là:
(km/h).
Vậy vận tốc trung bình của xe là: 24km/h.
