A = 2 + 2² +...+ 2⁹⁹ + 2¹⁰⁰

2A = 2² + 2³ + ... + 2¹⁰¹

2A − A = (2² + 2³ + .... + 2¹⁰¹) − (2 + 2² + ... + 2¹⁰⁰)

A = 2¹⁰¹ – 2.

Lời giải

Trung bình cộng của hai số là: 45 – 7 = 38

Tổng của hai số là: 38 × 2 = 76

Số bé là: 76 – 45 = 31

Đáp số: 31.

Ta có: $2x^2+\frac{1}{x^2}+\frac{y^2}{4}=4$

$\iff \left(x^2-2+\frac{1}{x^2}\right)+\left(x^2+\frac{y^2}{4}\right)-2=0$

$\iff {\left(x-\frac{1}{x}\right)}^2+\left(x^2+xy+\frac{y^2}{4}\right)-xy-2=0$

$\iff {\left(x-\frac{1}{x}\right)}^2+{\left(x+\frac{y}{2}\right)}^2-xy-2=0$

$\Rightarrow xy+2={\left(x-\frac{1}{x}\right)}^2+{\left(x+\frac{y}{2}\right)}^2$

Do ${\left(x-\frac{1}{x}\right)}^2\ge 0$  với mọi x ≠ 0,  ${\left(x+\frac{y}{2}\right)}^2\ge 0$với mọi x, y

⇒ P = xy + 2 ≥ 0

⇒ P = xy ≥ ‒2

Dấu “=” xảy ra khi và chỉ khi $\left\{\begin{array}{l}x-\frac{1}{x}=0\\ x+\frac{y}{2}=0\end{array}\right.\iff \left\{\begin{array}{l}x=-1\\ y=2\end{array}\right.$   hoặc $\left\{\begin{array}{l}x=1\\ y=-2\end{array}\right.$ .

Vậy giá trị nhỏ nhất của P là ‒2 khi (x; y) ∈ {(–1; 2); (1; –2)}.

Tập hợp A số nhỏ nhất là 1, số lớn nhất là 301 hai số kế tiếp cách nhau 3 đơn vị.

Do đó số phần tử của tập hợp A là : (301 -1) : 3 + 1 = 101 (phần tử).

Tương tự, tập hợp B số nhỏ nhất là 8, số lớn nhất là 30 hai số kế tiếp cách nhau 2 đơn vị.

Tập hợp B có (30 – 8) : 2 + 1 = 12 (phần tử).

Gọi số phải tìm là a, a ∈ ℕ*

Vì a chia cho 17, 25 được các số dư theo thứ tự là 8 và 16 nên a + 9 chia hết cho 8 và 16

Suy ra (a + 9) ∈ BC (8, 16)

⇒ BCNN (8, 16) = 16

⇒ a + 9 ∈ B (16) = 16k (k ∈ ℕ)

Vậy số tự nhiên a phải tìm có dạng a = 16k ‒ 9.

x(x + 4) ‒ x² = 10

⇔ x² + 4x ‒ x² =10

⇔ 4x = 10

$\iff x=\frac{5}{2}$

Vậy $x=\frac{5}{2}$  .

$x-\frac{1}{2}=\frac{4}{3}-\left(2x+1,2\right)$

$\iff \frac{2x-1}{2}=\frac{4}{3}-2x-\frac{6}{5}=\frac{20-30x-24}{30}$

$\iff \left(2x-1\right).15=20-30x-24$

$\iff 30x-15=20-30x-24$

$\iff 60x=11$

$\iff x=\frac{11}{60}$

Vậy $x=\frac{11}{60}$  .

Cách 1:

Ô tô đi 1 km hết số lít xăng là: 12 : 100 = 0,12 (lít).

Ô tô đi 200 km hết số lít xăng là: 0,12 × 200 = 24 (lít)

Vậy nếu xe ô tô đó có 23 lít xăng thì không thể đi hết được quãng đường dài 200 km.

 Cách 2:

Ta có: 200 : 100 = 2.

Ô tô đi 200 km hết số lít xăng là: 12 × 2 = 24 (lít)

Vậy nếu xe ô tô đó có 23 lít xăng thì không thể đi hết được quãng đường dài 200 km.

Chu vi khu đất là : (48 + 25 ) × 2 = 146 (m)

Chiều dài khu dất cần rào là : 146 ‒ 2 = 144 (m)

Đổi 144m = 1440dm

Số tiền thuê rào hết khu đất là : 1440 × 2500 = 3 600 000 (đồng)

                     Đáp số: 3 600 000 đồng.

Vì 45 ⋮ 9; 63 ⋮ 9 ⇒ (45 + 63) ⋮ 9

Do đó để A = 45 + 63 + x ⋮ thì x ⋮ 9.

Số thứ năm bằng số trung bình cộng của bốn số còn lại nên số thứ năm bằng 1 phần thì tổng bốn số còn lại là 4 phần. 

Tổng của 5số là: 

1 + 4 = 5 (phần) 

Số thứ 5 là: 

600 : 5 × 1 = 120.

       Đáp số: 120.

Gọi x là số tự nhiên lớn nhất cần tìm (x ∈ ℕ*)

Vì 22, 32, 42 chia cho x đều có số dư là 2.

Do đó 20, 30, 40 chia hết cho x, hay x là ƯCLN(20, 30, 40)

Ta có: 20 = 2.2.5; 30 = 2.3.5; 40 = 2.4.5

⇒ ƯCLN(20, 30, 40) = 2.5 = 10

Vậy số cần tìm là 10.

Vì a chia 19 dư 3 nên a = 19m + 3

Vì b chia 38 dư 5 nên b = 38n + 5

Ta có:

   3a + 2b

= 3(19m + 3) + 2(38n + 5)

= 57m + 9 + 76n + 10

= 57m + 76n + 19

Vì 57m ⋮ 19; 76n ⋮ 19 và 19 ⋮ 19

Suy ra (57m + 76n + 19) ⋮ 19

Bội của 5 là những số nguyên có chữ số tận cùng là 0 hoặc 5.

Ta có:

A = 12 – x² – 6x

= – (x² + 6x – 12)

= – (x² + 6x + 9 – 21)

= – (x + 3)² + 21

Có (x + 3)² ≥ 0 với mọi x

⇒ – (x + 3)² ≤ 0 với mọi x

⇒ A = – (x + 3)² + 21 ≤ 21 với mọi x

Dấu “=” xảy ra khi (x + 3)² = 0

⇔ x + 3 = 0

⇔ x = – 3

Vậy giá trị lớn nhất của A = 21 khi x = – 3.

• Trường hợp 1: Nếu x < y ≤ 0 thì x – y < 0

Khi đó |x – y| = –(x – y) nên |x – y| – |x| + |y| = –(x – y) – x – y = –2x

Do x < 0 nên –2x > 0 hay |x – y| – |x| + |y| > 0

Do đó |x – y| > |x| – |y|.

• Trường hợp 2: Nếu x > y > 0 thì x – y > 0 nên |x – y| – |x| + |y| = x – y – x + y = 0

Do đó |x – y| = |x| – |y|.

• Trường hợp 3: Nếu x = y = 0 thì |x – y| – |x| + |y| = 0

Do đó |x – y| = |x| – |y|.

Kết hợp 3 TH ta có đpcm.

Một người ăn hết số gạo đó trong số ngày là:

10 × 180 = 1800 (ngày)

Số người ăn trên thực tế là:

180 – 30 = 150 (người)

Số gạo đó đủ ăn trong số ngày là:

1800 : 150 = 12 (ngày)

Nhóm các số hữu tỉ âm: $\frac{-13}{6}$ ;$\frac{-1}{5}$ ; $-3,7$

Ta có $\frac{-13}{6}=-2,6$ ; $\frac{-1}{5}=-0,2$

Vì ‒3,7 < ‒2,6 < ‒0,2 ⇒  (1)

Nhóm các số hữu tỉ dương: $\frac{21}{11}$  ;$1\frac{1}{2}$ ; $\frac{3}{7}$

Ta thấy: $\frac{21}{11}>1$ ; $1\frac{1}{2}>1$  ; $\frac{3}{7}<1$

Ta có:$\frac{21}{11}=\frac{42}{22}$ ; $1\frac{1}{2}=\frac{3}{2}=\frac{33}{22}$

Vì 33 < 42 nên $\frac{33}{22}<\frac{42}{22}$

Do đó:     $\frac{3}{7}<1\frac{1}{2}<\frac{21}{11}$      (2)

Từ (1) và (2) ⇒ $-3,7<\frac{-13}{7}<\frac{-1}{5}<\frac{3}{7}<1\frac{1}{2}<\frac{21}{11}$

Vậy các số được sắp xếp theo thứ tự tăng dần là: ‒3,7;$\frac{-13}{7}$ ; $\frac{-1}{5}$ ; $\frac{3}{7}$ ; $1\frac{1}{2}$  ; $\frac{21}{11}$  .

Số các số hạng của dãy số trên là:

   (247 ‒23) : 2 + 1 = 113 ( số hạng )

Tổng của dãy số trên là:

    (247 + 23) × 113 : 2 = 15 255

                Đáp số : 15 255

Gọi số cần tìm có dạng $\overline{abc}$  (a ≠ 0)

Vì số tận cùng là số lẻ c = 3 hoặc c = 5

• Với c = 3 thì a có 2 cách chọn (5 hoặc 6), b có 2 cách chọn (trừ chữ số 3 và chữ số a đã chọn).

   Þ có 2 . 2 = 4 số thõa mãn.

• Với c = 5 thì a có 2 cách chọn (3 hoặc 6), b có 2 cách chọn (trừ chữ số 5 và chữ số a đã chọn).

   Þ có 2 . 2 = 4 số thõa mãn.

Vậy có thể lập được 4 + 4 = 8 số thỏa mãn yêu cầu.

Ta có: a² – 2b = c² – 2a

⇔ a² – c² = 2b – 2a

⇔ (a – c).(a + c) = 2(b – a)

$\iff a+c=\frac{2\left(b-a\right)}{a-c}$

$\iff a+c+2=\frac{2\left(b-a\right)}{a-c}+2$

$\iff a+c+2=\frac{2\left(b-a\right)+2\left(a-c\right)}{a-c}$

$\iff a+c+2=\frac{2\left(b-c\right)}{a-c}$

Chứng minh tương tự ta có: $a+b+2=\frac{2\left(a-c\right)}{a-b}$  và $b+c+2=\frac{2\left(b-a\right)}{b-c}$

⇒ A = (a + b + 2).(b + c + 2).(c + a + 2)

         $=a+b+2=\frac{2\left(a-c\right)}{a-b}.\frac{2\left(b-a\right)}{b-c}.\frac{2\left(b-c\right)}{a-c}=-8$ .

Theo tính chất đường phân giác thì $\frac{BD}{DC}=\frac{AB}{AC}=\frac{c}{b}$

$\Rightarrow \overrightarrow{BD}=\frac{BD}{DC}.\overrightarrow{DC}=\frac{b}{c}.\overrightarrow{DC}$  (*)

Mặt khác $\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}$  và $\overrightarrow{DC}=\overrightarrow{AC}-\overrightarrow{AD}$

Thay vào (*) ta có: $\overrightarrow{AD}-\overrightarrow{AB}=\frac{b}{c}\overrightarrow{AC}-\overrightarrow{AD}$

$\iff b+c\overrightarrow{AD}=b\overrightarrow{AB}+c\overrightarrow{AC}$

$\iff b+c^2{\overrightarrow{AD}}^2=b{\overrightarrow{AB}}^2+2bc\overrightarrow{AB}.\overrightarrow{AC}+c{\overrightarrow{AC}}^2$

$\iff b+c^2{\overrightarrow{AD}}^2=b^2{c}^2+2bc.\frac{1}{2}{c}^2+b^2-a^2+c^2{b}^2$

$\iff {\overrightarrow{AD}}^2=\frac{bc}{b+c^2}.\left(b+c-a\right)\left(b+c+a\right)$

$\Rightarrow \overrightarrow{AD}=\sqrt{\frac{bc}{b+c^2}.\left(b+c-a\right)\left(b+c+a\right)}$.

a)

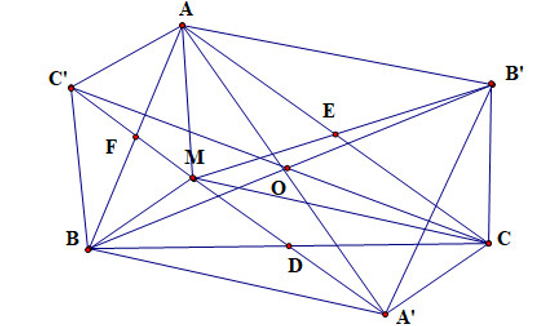
Xét tứ giác AB’CM có:

AC cắt MB’ tại trung điểm E của mỗi đường và AC, MB’ là hai đường chéo.

⇒ AB’CM là hình bình hành.

Do đó AB' // MC, AB' = MC

Xét tứ giác BMCA’ có

BC cắt MA’ tại trung điểm D của mỗi đường và BC, MA’ là hai đường chéo.

⇒ BMCA’ là hình bình hành.

Do đó MC // A’B, MC = A'B.

Ta có AB’ // MC, MC // A'B (chứng minh trên), suy ra AB’ // A’B.

Ta có MC = A’B, AB’ = MC (chứng minh trên), suy ra AB’ = A’B.

Xét tứ giác AB’A’B có AB’ // A’B và AB’ = A’B

⇒ Tứ giác AB’A’B là hình bình hành.

b) Xét hình bình hành AB’A’B có AA’ và BB’ cắt nhau tại O.

⇒ O là trung điểm của AA’.

Chứng minh tương tự câu a ta có: AC’ = A’C (= BM) và AC’ // A’C (// BM)

⇒ AC’A’C là hình bình hành.

Mà O là trung điểm của AA’

Suy ra O là trung điểm của CC’.

Hay C và C’ đối xứng nhau qua điểm O.

Vậy C và C’ đối xứng nhau qua điểm O.

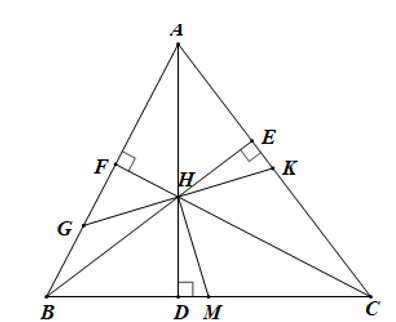
Ta có:$\widehat{GHF}+\widehat{HGF}=90°$  (do DGHF vuông tại F) và $\widehat{CHM}+\widehat{CHK}=90°$

Mà $\widehat{GHF}=\widehat{CHK}$   (đối đỉnh) nên $\widehat{HGF}=\widehat{CHM}$  hay $\widehat{HGA}=\widehat{CHM}$

Ta có: $\widehat{BAD}+\widehat{ABD}=90°$  (do DABD vuông tại D);

          $\widehat{BCF}+\widehat{CBF}=90°$  (do DBCF vuông tại F)

Do đó $\widehat{BAD}=\widehat{BCF}$  hay $\widehat{GAH}=\widehat{MCH}$

Xét DGAH và DCHM có: $\widehat{HGA}=\widehat{CHM}$và $\widehat{GAH}=\widehat{MCH}$

Do đó $\Delta GAH \backsim \Delta HCM\left(g.g\right)$

Suy ra $\frac{GH}{HM}=\frac{AH}{CM}$  (tỉ  số đồng dạng) (1)

Tương tự, ta có: $\Delta AHK \backsim \Delta BMH\left(g.g\right)$

Suy ra $\frac{AH}{BM}=\frac{HK}{MH}$  (tỉ số đồng dạng) (2)

Mặt khác: M là trung điểm của BC nên CM = BM (3)

Từ (1), (2) và (3) ta có:$\frac{GH}{HM}=\frac{HK}{MH}$ , suy ra GH = HK.

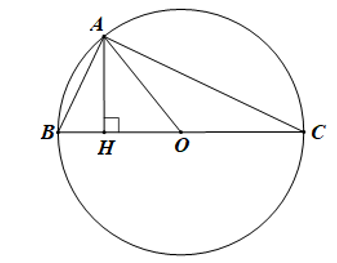
a) Ta có: OA = OB = OC = R

⇒ $OA=\frac{BC}{2}$

• Trong ΔABC, AO là đường trung tuyến và $OA=\frac{BC}{2}$  nên ΔABC vuông tại A.

b) Kẻ đường cao AH của tam giác ABC

Ta có: $S_{ABC}=\frac{1}{2}BC.AH=\frac{1}{2}.2R.AH=R.AH$

Trong tam giác vuông AHO, ta có:

AH ≤ AO (cạnh góc vuông nhỏ hơn cạnh huyền)

Hay AH ≤ R ⇒ AH.R ≤ R²

Vậy $S_{ABC}\le R^2$

Dấu “=” xảy ra khi A trùng với các đầu mút của đường kính vuông góc với BC.

a) Đúng. 2 và 3 là hai số tự nhiên liên tiếp và đều là số nguyên tố.

b) Đúng. 3; 5; 7 là ba số lẻ liên tiếp và đều là số nguyên tố.

c) Sai vì có số 2 là số nguyên tố chẵn.

d) Sai vì 2 là số nguyên tố và không tận cùng bằng các chữ số trên.

Vậy ta có bảng sau:

a) 2; 3.

b) 3; 5; 7.

Sau khi chuyển đi 80 người thì còn lại số người là:

120 ‒ 80 = 40 (người)

Lúc đầu, một người ăn hết số gạo đó trong số ngày là:

120 × 18 = 2160 (ngày)

40 người ăn hết số gạo đó trong số ngày là:

2160 : 40 = 54 (ngày)

Một người ăn hết số gạo đó trong số ngày là:

18 × 120 = 2160 (ngày)

Số người ăn trên thực tế là:

120 – 12 = 108 (người)

Số gạo đó đủ ăn trong số ngày là:

2160 : 168 = 20 (ngày)

Một người ăn hết số gạo đó trong số ngày là:

27 × 80  = 2160 (ngày)

Số người ăn trên thực tế là:

80 + 40 = 120 (người)

Số gạo đó đủ ăn trong số ngày là:

2160 : 120 = 18 (ngày)

Chiều rộng căn phòng là

$8\times \frac{3}{4}=6$(m)

Diện tích căn phòng là:

8 × 6 = 48 (m²)

Diện tích một viên gạch là

4 × 4 = 16 (dm²)

Đổi 48 m² = 4800dm²

Số viên gạch cần dùng để lát kín căn phòng là :

4800 : 16 = 300 (viên gạch)

Số gạo còn lại sau khi bán lần 1 là:

$1-\frac{2}{7}=\frac{5}{7}$(số gạo)

Số gạo ngày thứ hai bán được là:

$\frac{1}{3}.\frac{5}{7}=\frac{5}{21}$(số gạo)

Số gạo còn lại tương ứng với số phần gạo là:

$1-\left(\frac{2}{7}+\frac{5}{21}\right)=\frac{10}{21}$ (số gạo)

Số kilogam gạo ban đầu là:

$300:\frac{10}{21}=630$(kg)

Đổi 7m 2dm = 0,72 dam; $\frac{18}{25}$  dam² = 0,72 dam²

Chiều dài hình chữ nhật là:

        0,72 : 0,72 = 1(dam)

Chu vi hình chữ nhật là:

       (1 + 0,72) × 2 = 3,44(dam)

Cạnh hình vuông là:

        3,44 : 4 = 0,86 (dam)

       Đổi: 0,86 dam = 86 dm.

Đổi $\frac{1}{10}$ hm² = 1000 m²

Chiều rộng thửa ruộng hình chữ nhật là:

1000 : 125 = 8 (m)

Chu vi thửa ruộng hình chữ nhật là:

(125 + 8) × 2 = 266 (m)

Tỉ số của chiều dài và chiều rộng là: 2 : 1.

Nếu chiều dài là 2 phần thì chiều rộng bằng 1 phần

Hiệu số phần bằng nhau là:                                                             

2 ‒ 1 = 1 (phần)                                                                             

Chiều dài vườn hoa là:                                                                     

 20 × 2 = 40 (m).                                                                         

Chiều rộng vườn hoa là :                                                                        

40 ‒ 20 = 20 (m).                                                                    

Chu vi vườn hoa là:                                                                             

 (40 + 20) × 2 = 120 (m).                                                                    

Diện tích vườn hoa là:                                                                           

40 × 20 = 800 (m²).

Mẫu số chung: 20

$\frac{2}{5}=\frac{2\times 4}{5\times 4}=\frac{8}{20}$

$\frac{3}{4}=\frac{3\times 5}{4\times 5}=\frac{15}{20}$

Vì  $\frac{8}{20}<\frac{15}{20}$nên $\frac{2}{5}<\frac{3}{4}$ .

Số lẻ nhỏ nhất có 3 chữ số là: 101

Tổng 2 số là: 138 × 2 =276

Số thứ hai là: 276 − 101 = 175.

Tích mới hơn tích cũ là: 850 – 476 = 374

Tích mới hơn tích cũ là 374 vì được thêm 22 lần thừa số kia.

Thừa số thứ hai là: 374 : 22 = 17

Thừa số thứ nhất là: 476 : 17 = 28.

Vậy hai số cần tìm là: 17 và 28

Vì n chia 8 dư 7 nên n = 8a + 7 với a ∈ N ⇒ (n + 1) ⋮ 8

Vì n chia 31 dư 28 nên n = 31b + 28 (b ∈ N) ⇒ (n + 3) ⋮ 31

Vì 64 ⋮ 8 nên (n + 1 + 64) ⋮ 8 hay (n + 65) ⋮ 8 (1)

Vì 62 ⋮ 31 ⇒ (n + 3 + 62) ⋮ 31 hay (n + 65) ⋮ 31 (2)

Từ (1) và (2) ⇒ (n + 65) ⋮ BCNN(8; 31)

(n + 65) ⋮ 248

⇒ n = 248k ‒ 65 (k ∈ ℕ*)

Với k = 1 ⇒ n = 248.1 ‒ 65 = 183

Với k = 2 ⇒ n = 248.2 ‒ 65 = 431

Với k = 3 ⇒ n = 248.3 ‒ 65 = 679

Với k = 4 ⇒ n = 248.4 ‒ 65 = 927

Với k = 5 ⇒ n = 248.5 ‒ 65 = 1175 (loại)

Vì n là số lớn nhất có ba chữ số nên n = 927

Số phần mà số tiền Bình góp chiếm là:  $\frac{1}{4}.\frac{3}{2}=\frac{3}{8}$(tổng số phần).

Số phần mà số tiền Chí góp chiếm là: $1-\frac{1}{4}-\frac{3}{8}=\frac{3}{8}$  (tổng số phần).

Giá tiền quả bóng là: $24000:\frac{3}{8}=64000$  (đồng).