Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 11)
-
2062 lượt thi
-
59 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Một chiếc xe đạp giá 400 000 đồng, nay hạ giá 15%. Hỏi giá tiền chiếc xe đạp bây giờ là bao nhiêu?
 Xem đáp án
Xem đáp án
Giá tiền hạ là:
400 000 × 15% = 60 000 (đồng)
Giá tiền chiếc xe đạp bây giờ là:
400 000 – 60 000 = 340 000 (đồng)
Đáp số: 340 000 đồng.
Câu 2:
Nam đi xe máy từ thành phố về quê. Nam dự tính về đến quê lúc 11 giờ để dự đám cưới. Nếu Nam đi với vận tốc 25 km/giờ thì về đến quê chậm 2 giờ. Còn nếu đi với vận tốc 30 km/giờ thì về đến quê chậm 1 giờ. Hỏi quãng đường từ thành phố về quê dài bao nhiêu?
 Xem đáp án
Xem đáp án
Tỉ số giữa vận tốc 25 km/giờ và vận tốc 30 km/giờ là:
Vậy thời gian đi với vận tốc 25 km/giờ = thời gian đi với vận tốc 30 km/giờ (vì trên cùng quãng đường, thời gian và vận tốc là hai đại lượng tỉ lệ nghịch).
Hiệu thời gian đi với vận tốc 25 km/giờ và thời gian đi với vận tốc 30 km/giờ là:
2 – 1 = 1 (giờ)
Thời gian đi với vận tốc 25 km/giờ là:
1 : (6 – 5) × 6 = 6 (giờ)
Quãng đường từ thành phố về quê dài:
6 × 25 = 150 (km)
Đáp số: 150 km.
Câu 3:
Một đơn vị bội đội đã chuẩn bị gạo cho 120 người ăn trong 50 ngày, nhưng sau đó người của đơn vị lên đến 200 người. Hỏi số gạo đủ ăn trong bao nhiêu ngày? (Mức ăn như nhau).
 Xem đáp án
Xem đáp án
Số người ăn tỉ lệ nghịch với số ngày vì số gạo không thay đổi nên số người ăn tăng lên bao nhiêu lần thì số ngày ăn sẽ giảm đi bấy nhiêu lần (và ngược lại).
Số gạo đó đủ cho 1 người ăn trong :
120 × 50 = 6000 (ngày)
Số gạo đó đủ cho 200 người ăn trong:
6000 : 200 = 30 (ngày)
Đáp số: 30 ngày.
Câu 4:
Công trường dự định huy động 240 công nhân làm việc trong 7 ngày để sửa xong một quãng đê. Sau 3 ngày làm việc thì được bổ sung thêm 80 người nữa. Hỏi phải tiếp tục làm bao nhiêu ngày nữa thì công trường sẽ sửa xong quãng đê? (năng suất mọi người đều như nhau).
 Xem đáp án
Xem đáp án
Số công nhân và số ngày làm tỉ lệ nghịch với nhau vì cùng một khối lượng công việc, số công nhân tăng lên bao nhiêu lần thì số ngày làm giảm đi bấy nhiêu lần (và ngược lại).
Số ngày còn lại phải làm theo dự định là
7 – 3 = 4 (ngày)
Số người sau khi được bổ sung là:
240 + 80 = 320 (người)
Ta có:
240 công nhân ––––––––– 4 ngày
320 công nhân ––––––––– … ngày ?
Nếu 1 công nhân làm thì cần số ngày là:
240 × 4 = 960 (ngày)
Vậy 320 công nhân làm trong số ngày là:
960 : 320 = 3 (ngày)
Đáp số: 3 ngày.
Câu 5:
So sánh A với B biết:
B = (27,5 × 0,1 + 2,5 × 0,1) × 2.
 Xem đáp án
Xem đáp án
Lời giải:
B = (27,5 × 0,1 + 2,5 × 0,1) x 2
= [(27,5 + 2,5) × 0,1] × 2
= (30 × 0,1) × 2
= 6
Suy ra A < B (vì 3 < 6).
Câu 6:
Tìm một phân số tối giản khác 0 biết rằng tổng của nó và phân số nghịch đảo của nó là .
 Xem đáp án
Xem đáp án
Gọi phân số cần tìm là .
Theo đề bài ta có:
Ta thấy
Đặt
Vậy phân số cần tìm là: .
Câu 7:
Tính tổng các số hạng của dãy số cách đều: 1, 4, 7, 10, 13,…, 55, 58.
 Xem đáp án
Xem đáp án
Ta thấy:
4 = 1 + 3
7 = 4 + 3
10 = 7 + 3
13 = 10 + 3
…
55 = 52 + 3
58 = 55 + 3
Vậy quy luật của dãy số này là: mỗi số kể từ số thứ hai bằng số liền trước cộng thêm 3 đơn vị.
Số các số hạng trong dãy số trên là:
(58 – 1) : 3 + 1 = 20 (số)
Tổng các số hạng của dãy số trên là:
(58 + 1) × 20 : 2 = 590
Đáp số: 590.
Câu 8:
Tổng của hai số là 0,6. Thương của hai số đó cũng bằng 0,6. Tìm hai số đó.
 Xem đáp án
Xem đáp án
Vì thương của số bé và số lớn là 0,6 nên số bé bằng số lớn.
Ta coi số bé là 3 phần bằng nhau thì số lớn là 5 phần bằng nhau.
Tổng số phần bằng nhau là: 3 + 5 = 8 phần
Giá trị 1 phần là: 0,6 : 8 = 0,075
Số bé: 0,075 × 3 = 0,225
Số lớn: 0,6 – 0,225 = 0,375.
Câu 9:
Một kho gạo có 537,25 tấn gạo. Người ta đã lấy ra số gạo trong kho. Hỏi trong kho còn lại bao nhiêu tấn gạo?
 Xem đáp án
Xem đáp án
Số tấn gạo người ta đã lấy ra là:
(tấn)
Trong kho còn lại số gạo là:
537,25 – 53,725 = 483, 525 (tấn)
Đáp số: 483, 525 tấn gạo.
Câu 11:
Chứng minh rằng với mọi giá trị của m thì phương trình luôn có nghiệm.
 Xem đáp án
Xem đáp án
Ta có:
Xét có:
Vậy phương trình luôn có nghiệm với mọi m.
Câu 12:
May một cái áo hết 1,55 m vải. May một cái quần hết 2,05 m vải. Hỏi có 202 m vải may được bao nhiêu bộ quần áo như thế và còn thừa mấy mét vải?
 Xem đáp án
Xem đáp án
May 1 bộ quần áo hết số vải là:
1,55 + 2,05 = 3,6 (m)
202 m vải may được số bộ quần áo là:
202 : 3,6 = 56 (bộ) và còn thừa 0,4 m vải.
Đáp số: 56 bộ và 0,4 m vải.
Câu 13:
Mẹ hơn con 24 tuổi. Tuổi mẹ gấp 3 lần tuổi con. Hỏi mẹ bao nhiêu tuổi, con bao nhiêu tuổi?
 Xem đáp án
Xem đáp án
Hiệu số phần là:
3 – 1 = 2 phần
Tuổi con là:
24 : 2 × 1 = 12 (tuổi)
Tuổi mẹ là:
24 + 12 = 36 (tuổi)
Đáp số: Con: 12 tuổi, mẹ 36 tuổi.
Câu 14:
Một can xăng đựng 8,5 lít xăng cân nặng 8,22 kg, vỏ can cân nặng 1,25kg. Hỏi một thùng xăng cùng loại có 28,3 lít xăng cân nặng bao nhiêu kg, biết vỏ thùng cân nặng 3,08 kg?
 Xem đáp án
Xem đáp án
8,5 lít xăng nặng số kg là:
8,22 – 1,25 = 6,97 (kg)
1 lít xăng nặng số kg là:
6,97 : 8,5 = 0,82 (kg)
28,3 lít xăng nặng số kg là:
28,3 × 0,82 = 23,206 (kg)
Một thùng xăng chứa 28,3 lít xăng nặng số kg là:
23,206 + 3,08 = 26,286 (kg)
Đáp số: 26,286 kg.
Câu 15:
Một hình chữ nhật có chu vi là 36 cm. Chiều dài hơn chiều rộng 2 cm. Tính diện tích hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Nửa chu vi hình chữ nhật là:
36 : 2 = 18 (cm)
Chiều rộng hình chữ nhật là:
(18 – 2) : 2 = 8 (cm)
Chiều dài hình chữ nhật là:
8 + 2 = 10 (cm)
Diện tích hình chữ nhật là:
10 × 8 = 80 (cm2)
Đáp số: 80 cm2.
Câu 16:
Một hình chữ nhật có chu vi là 56 cm. Chiều dài hơn chiều rộng 12 cm. Tính diện tích hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Nửa chu vi hình chữ nhật là:
56 : 2 = 28 (cm)
Chiều dài hình chữ nhật là:
(28 + 12) : 2 = 20 (cm)
Chiều rộng hình chữ nhật là:
28 – 20 = 8 (cm)
Diện tích hình chữ nhật là:
20 × 8 = 160 (cm2)
Đáp án: 160 cm2.
Câu 17:
Một hình thang có diện tích 20 m2, đáy lớn 55 dm và đáy bé 45 dm. Tính chiều cao của hình thang.
 Xem đáp án
Xem đáp án
Đổi
Chiều cao hình thang là:
2000 × 2 : (55 + 45) = 40 (dm)
Đáp số: 40 dm.
Câu 18:
Nếu tăng cạnh đáy của hình tam giác lên 2 lần, chiều cao lên 3 lần thì diện tích hình tam giác đó tăng lên bao nhiêu lần?
 Xem đáp án
Xem đáp án
Gọi độ dài cạnh đáy tam giác là a, chiều cao là h.
Ta có diện tích tam giác
Nếu đáy tam giác tăng lên 2 lần thì độ dài mới là: 2a
Chiều cao tăng lên 3 lần thì chiều cao mới là: 3h
Diện tích mới là:
Vậy diện tích tam giác tăng lên:
(lần).
Câu 19:
Chiều rộng của một đám đất hình chữ nhật là 16,5m. Chiều rộng bằng chiều dài. Trên thửa ruộng đó người ta trồng cà chua. Hỏi người ta thu hoạch được bao nhiêu tạ cà chua biết mỗi mét vuông thu hoạch được 6,8kg cà chua?
 Xem đáp án
Xem đáp án
Chiều dài đám đất là:
16,5 × 3 = 49,5 (m)
Diện tích đám đất hình chữ nhật là:
49,5 × 16,5 = 816,75 (m2)
Người ta thu hoạch được:
816,75 × 6,8 = 5553,9 (kg) = 55, 539 tạ
Đáp số: 55,539 tạ cà chua.
Câu 20:
 Xem đáp án
Xem đáp án
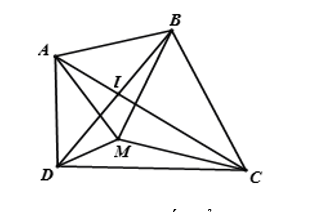
Gọi I là giao điểm của AC và BD. Ta có các bất đẳng thức:
MA + MC AC
MB + MD BD
Từ đó suy ra:
MA + MB + MC + MD AC + BD
MA + MB + MC + MD nhỏ nhất khi MA + MB + MC + MD = AC + BD khi M trùng với I.
Vậy khi M là giao điểm hai đường chéo thì MA + MB + MC + MD nhỏ nhất.
Câu 21:
Một kho gạo có 537,25 tấn gạo. Người ta lấy ra số gạo trong kho. Hỏi trong kho còn bao nhiêu tấn gạo?
 Xem đáp án
Xem đáp án
Số gạo đã lấy ra là:
537,25 : 10 = 53,725 (tấn)
Số gạo còn lại trong kho là:
537,25 – 53,725 = 483,525 (tấn)
Đáp số: 483,525 (tấn)
Câu 22:
Ba thùng nước mắm đựng được 96 l. Hỏi 5 thùng như thế thì đựng được bao nhiêu lít nước mắm như thế?
 Xem đáp án
Xem đáp án
Số thùng nước mắm và số lít nước mắm tỉ lệ thuận với nhau.
1 thùng đựng được: 96 : 3 = 32 (l)
Vậy 5 thùng đựng được: 32 × 5 = 160 (l)
Đáp số: 160 lít.
Câu 23:
Trong 2 ngày với 8 người thì sửa được 64 m đường. Vậy trong 5 ngày với 9 người thì sửa được bao nhiêu mét đường? (năng suất mỗi người như nhau)
 Xem đáp án
Xem đáp án
Trong 1 ngày 8 người sửa được:
64 : 2 = 32 (m)
Trong 5 ngày 8 người sửa được:
32 × 5 = 160 (m)
Trong 5 ngày 1 người sửa được:
160 : 8 = 20 (m)
Trong 5 ngày 9 người sửa được:
20 × 9 = 180 (m)
Đáp số: 180 m.
Câu 24:
Tính A = 1.2 + 2.3 + 3.4 +…+ (n – 1).n
 Xem đáp án
Xem đáp án
Nhân 3 vào hai vế ta được:
3A = 3. [1.2 + 2.3 + 3.4 +…+ (n – 1).n]
3A = 1.2.3 + 2.3.3 + 3.4.3 +…+ (n – 1).n.3
3A = 1.2.3 + 2.3.(4 – 1) + 3.4.(5 – 2) +…+ (n – 1).n.[(n + 1) – (n – 2)]
3A = 1.2.3 + 2.3.4 – 1.2.3 + 3.4.5 – 2.3.4 +…+ (n – 1).n.(n + 1) – (n – 2).(n – 1).n
3A = (n – 1).n.(n + 1)
Suy ra A = .
Câu 25:
Tính:
a, (–90 + 150) – (10 – 50).
b, 1 – 2 – 3 + 4 + 5 – 6 – 7 + 8 + …+ 997 – 998 – 999 + 1000.
 Xem đáp án
Xem đáp án
a, (–90 + 150) – (10 – 50)
= –90 + 150 – 10 + 50
= (–90 – 10) +(150 + 50)
= –100 + 200 = 100.
b, 1 – 2 – 3 + 4 + 5 – 6 – 7 + 8 + …+ 997 – 998 – 999 + 1000.
= (1 – 2 – 3 + 4) + (5 – 6 – 7 + 8) +…+ (997 – 998 – 999 + 1000)
=0 + 0 + …+ 0 = 0.
Câu 26:
Cho a, b, c > 0 thỏa mãn . Tìm GTNN: .
 Xem đáp án
Xem đáp án
Đặt A =
4A =
=
Áp dụng bất đẳng thức AM – GM:
Dấu “=” xảy ra a = 2, b = 3, c = 4.
Câu 27:
Có 50 chai sữa, mỗi chai có 0,5 lít sữa. Mỗi lít sữa cân nặng 1,02 kg. Mỗi vỏ chai cân nặng 0,2 kg. Hỏi 50 chai sữa đó cân nặng tất cả bao nhiêu kg?
 Xem đáp án
Xem đáp án
Sữa trong 50 chai nặng:
50 × 0,5 × 1,02 = 25,5 (kg)
50 vỏ chai nặng:
50 × 0,2 = 10 (kg)
Vậy 50 chai sữa đó cân nặng tất cả:
25,5 + 10 = 35,5 (kg)
Đáp số: 35,5 kg.
Câu 28:
Tìm các số nguyên x biết: x + 1 là ước của x + 32.
 Xem đáp án
Xem đáp án
x + 32 = x + 1 + 31
x + 1 là ước của x + 32 (x + 32) ⁝ (x + 1) 31 ⁝ (x + 1)
x + 1 {1; –1; 31; –31}
x {0; – 2; 30; –32}.
Câu 29:
Hãy rút gọn phép tính: 1 × 2 + 2 × 3 + 3 × 4 +…+ n × (n + 1).
 Xem đáp án
Xem đáp án
Đặt A = 1 × 2 + 2 × 3 + 3 × 4 +…+ n × (n + 1)
3A = 1 × 2 × 3 + 2 × 3 × 3 + 3 × 4 × 3 +…+ n × (n + 1) × 3
3A = 1 × 2 × (3 – 0) + 2 × 3 × (4 – 1) + 3 × 4 × (5 – 2) +…+ n × (n + 1) × [(n + 2) – (n – 1)]
3A = 1 × 2 × 3 – 0 × 1 × 2 + 2 × 3 × 4 – 1 × 2 × 3 + 3 × 4 × 5 – 2 × 3 × 4 +…+ n × (n + 1) × (n + 2) – n × (n + 1) × (n – 1)
3A = n × (n + 1) × (n + 2)
Suy ra A = .
Câu 30:
Chứng tỏ rằng là phân số tối giản (n là số tự nhiên).
 Xem đáp án
Xem đáp án
Gọi d = ƯCLN(14n + 3; 21n + 4)
Khi đó
[3. (14n + 3) – 2. (21n + 4)] d
(42n + 9 – 42n – 8) d
1 d
Khi đó ta có d = 1.
Vậy ƯCLN(14n + 3; 21n + 4) = 1 hay là phân số tối giản (n là số tự nhiên).
Câu 31:
Tìm x, y, z biết 6x = 4y = 3z và 2x + 3y – 5z = –21.
 Xem đáp án
Xem đáp án
Lời giải:
6x = 4y = 3z
Áp dụng tính chất của dãy số bằng nhau ta có:
=
Vậy x = 6; y = 9; z = 12.
Câu 32:
Tìm Min với ; x, y > 0.
 Xem đáp án
Xem đáp án
Đặt t = xy
Theo BĐT AM– GM: do đó
Thấy
Dấu “=” xảy ra khi t = 2 (thỏa mãn điều kiện)
Vậy A min = 45 .
Câu 33:
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Vẽ hình bình hành ACEF trong có đó CE bằng cạnh của hình thoi. Vẽ G đối xứng với F qua A.
a) E, O, G thẳng hàng;
 Xem đáp án
Xem đáp án
a)
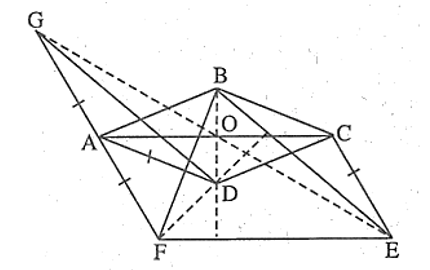
Vì G đối xứng với F qua A nên G, A, F thẳng hàng và GA = AF.
Ta có: AF // = CE (do ACEF là hình bình hành) nên AG // = CE.
Do đó tứ giác AGCE là hình bình hành có hai đường chéo là AC và GE.
Lại có ABCD là hình thoi có hai đường chéo AC và BD cắt nhau tại O nên O là trung điểm của AC và BD.
Vậy O là trung điểm của GE nên G, O, E thẳng hàng.
Câu 34:
b) GD // BE;
 Xem đáp án
Xem đáp án
b) Xét tứ giác GBED có hai đường chéo GE và BD cắt nhau tại trung điểm O của mỗi đường nên GBED là hình bình hành.
Do đó, GD // BE.
Câu 35:
c) D là trực tâm của tam giác BEF.
 Xem đáp án
Xem đáp án
c) Ta có CE = AD (CE bằng cạnh hình thoi ABCD)
Mà CE = AG = AF nên AD = AG = AF. Suy ra
Do đó, tam giác GDF vuông tại D.
Suy ra GD ⊥ DF.
Mà GD // BE (do GBED là hình bình hành) nên DF ⊥ BE.
Do ABCD là hình thoi nên AC ⊥ BD
Mà AC // EF (do ACEF là hình bình hành)
Nên EF ⊥ BD.
Xét tam giác BEF có DF ⊥ BE và EF ⊥ BD nên D là giao của hai đường cao của tam giác BEF, do đó D là giao của 3 đường cao của tam giác BEF. Vậy D là trực tâm của tam giác BEF.
Câu 36:
 Xem đáp án
Xem đáp án
Vì α là góc tù nên
Do đó:
(do α tù)
M = sinα – 2cosα = (sinα – cosα) – cosα = .
Câu 37:
 Xem đáp án
Xem đáp án
2x = 3y; 4y = 5z
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Vậy x, y, z lần lượt là 30, 20, 16.
Câu 38:
 Xem đáp án
Xem đáp án
2x = 5y = 3z
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Vậy x, y, z lần lượt là –60, –24, –40.
Câu 39:
Tính bằng cách hợp lí nhất: 89 : 0,25 + 89 : 0,2 + 89.
 Xem đáp án
Xem đáp án
89 : 0,25 + 89 : 0,2 + 89
= 89 × 4 + 89 × 5 + 89
= 89 × (4 + 5 + 1)
=89 × 10
= 890.
Câu 40:
Cho các số nguyên dương a, b, c, d thỏa mãn ab = cd. Chứng minh rằng: A = là hợp số với mọi số tự nhiên n.
 Xem đáp án
Xem đáp án
Ta có ab = cd
Đặt
Ta xét 2 TH sau:
Nếu k = 1
chia hết cho 2 và lớn hơn 2.
A là hợp số.
Nếu k khác 1:
là hợp số.
Vậy A = là hợp số với mọi số tự nhiên n.
Câu 41:
Cho A, B, C thuộc ℕ. Biết tích ab là số liền sau của tích cd và a + b = c + d. Chứng minh rằng a = b.
 Xem đáp án
Xem đáp án
Từ a + b = c + d suy ra d = a + b – c
Vì tích ab là số liền sau của tích cd nên ab = cd + 1 hay ab – cd = 1
ab – c . (a + b – c) = 1
ab – ac – bc + = 1
a. (b – c) – c. (b – c) = 1
(b – c) . (a – c) = 1
Suy ra a – c = b – c (vì cùng bằng 1 hoặc –1) suy ra a = b (đpcm)
Câu 42:
Tổng của hai số lẻ bằng 84. Tìm hai số đó biết giữa chúng cách nhau 2 số lẻ.
 Xem đáp án
Xem đáp án
Hai số lẻ hơn kém nhau một khoảng là hai đơn vị.
Giữa hai số lẻ cần tìm cách nhau 2 số lẻ do đó chúng cách nhau 3 khoảng như vậy.
Hiệu hai số lẻ cần tìm là:
2 × 3 = 6 (đơn vị)
Số lẻ thứ nhất là:
(84 – 6) : 2 = 39
Số lẻ thứ hai là:
84 – 39 = 45
Đáp số: 39 và 45.
Câu 43:
Bể thứ nhất chứa 1800 l nước, bể thứ hai chứa 1050 l nước. Cùng một lúc người ta rút nước ở hai bể ra, mỗi phút bể thứ nhất rút được 37,5 l nước, bể thứ hai rút được 25 l nước. Hỏi sau bao lâu thì lượng nước ở hai bể bằng nhau?
 Xem đáp án
Xem đáp án
Bể thứ nhất nhiều hơn bể thứ hai số lít nước là :
1800 – 1050 = 750 (l)
Mỗi phút bể thứ nhất rút được nhiều nước hơn bể thứ hai số lít nước là
37,5 – 25 = 12,5 (l)
Để hai bể bằng nhau thì vòi bể thứ nhất chảy hơn bể thứ hai 750 lít nước
Để hai bể bằng nhau thì sau số giờ là:
750 : 12,5 = 60 (phút) = 1 giờ
Đáp số: 1 giờ.
Câu 44:
Cho x, y là hai số thực thỏa mãn x + 2y = 1. Tìm GTLN của biểu thức P = xy.
 Xem đáp án
Xem đáp án
Từ x + 2y = 1 x = 1 – 2y
Ta có: P = xy = (1 – 2y). y =
Hay P ≤
Dấu “=” xảy ra
Câu 45:
Với x, y là các số dương thỏa mãn x + y = 6. Tìm GTNN của
.
 Xem đáp án
Xem đáp án
Với x, y là các số dương ta có:
(1)
(2)
Từ (1) và (2)
Dấu “=” xảy ra
Vậy khi x = y = 3.
Câu 46:
Với x, y là các số dương thỏa mãn x + y = 6. Tìm GTNN của
.
 Xem đáp án
Xem đáp án
Với x, y là các số dương ta có:
(1)
(2)
Từ (1) và (2)
Dấu “=” xảy ra
Vậy khi x = y = 3.
Câu 47:
 Xem đáp án
Xem đáp án
Số hạng thứ 100 của dãy trên là:
(100 – 1) × 2 + 1 = 199
Đáp số: 199.
Câu 48:
Cho dãy số :1, 3, 6, 10, 15, 21,... Tìm số hạng thứ 100 của dãy.
 Xem đáp án
Xem đáp án
Số thứ 1: 1
Số thứ 2: 1 + 2 = 3
Số thứ 3: 1 + 2 + 3 = 6
Số thứ 4: 1 + 2 + 3 + 4 = 10
Số thứ 5: 1 + 2 + 3 + 4 + 5 = 15
...............
Số thứ 100: 1 + 2 + 3 + 4 +....+ 99 +100
Số các số hạng là: (100 – 1) : 1 + 1 = 100 ( số hạng)
Số cặp là: 100 : 2 = 50 (cặp)
Số thứ 100 là: (100 + 1) × 50 = 5050.
Câu 49:
Cho nửa đường tròn tâm O đường kính AB = 2R. Gọi C là trung điểm OA, tia Cx vuông góc AB, Cx cắt nửa đường tròn (O) tại I. Lấy K là 1 điểm bất kì trên CI (K khác C và I). AK cắt nửa đường tròn (O) tại M. Tiếp tuyến với (O) tại M cắt Cx tại N. BM cắt Cx tại D.
a) Chứng minh: 4 điểm A, C, M, D thuộc 1 đường tròn.
 Xem đáp án
Xem đáp án
a)
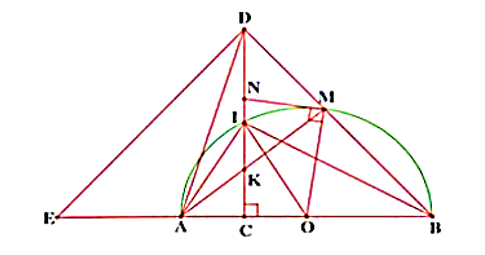
Ta có: (hai góc kề bù)
Mà (góc nội tiếp chắn nửa đường tròn).
Do đó, .
Lại có
(do Cx vuông góc với AB tại C).
Tứ giác ACMD có nên ACMD là tứ giác nội tiếp.
Vậy 4 điểm A, C, M, D thuộc 1 đường tròn.
Câu 50:
b) Chứng minh: tam giác MNK cân.
 Xem đáp án
Xem đáp án
b) Ta có: (góc tạo bởi tiếp tuyến và dây dung và góc nội tiếp cùng chắn một cung) (1).
Tứ giác BMKC có nên nó là tứ giác nội tiếp.
Suy ra (do cùng phụ với góc MKC). (2)
Từ (1) và (2) suy ra .
Vậy tam giác MNK cân tại N.
Câu 51:
c) Tính diện tích ABD khi K là trung điểm CI.
 Xem đáp án
Xem đáp án
c) AB là đường kính của (O) và AB = 2R nên OA = OB = R.
C là trung điểm của OA nên AC = .
Ta có: AC + BC = AB, suy ra BC = AB – AC = 2R – .
Tam giác AIB vuông tại I có IC là đường cao nên IC2 = AC . BC
Suy ra IC = .
Vì K là trung điểm của IC nên .
Xét hai tam giác ACK và DCB có:
(do ACMD là tứ giác nội tiếp)
Do đó .
Do đó, diện tích tam giác ABD là (đvdt).
Câu 52:
Cho đường tròn tâm O bán kính 13 cm và dây AB = 24 cm của đường tròn. Gọi I là trung điểm của AB. Từ A và B vẽ hai tiếp tuyến với đường tròn, cắt nhau tại C.
a, Vẽ hình và tính độ dài OI.
 Xem đáp án
Xem đáp án
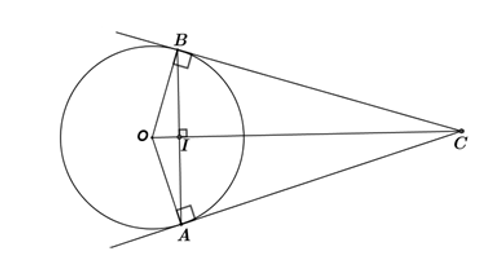
Do AB < 2R nên AB không đi qua O.
Xét tam giác OAB: OA = OB = R và I là trung điểm của AB.
OI là đường trung tuyến đồng thời là đường cao của cân tại O
Áp dụng định lí Pytago trong vuông tại I:
Câu 53:
 Xem đáp án
Xem đáp án
b, ta có CB và CA là hai tiếp tuyến của (O) cắt nhau tại C
AC = CB C thuộc đường trung trực của AB.
Lại có: OA = OB = R O thuộc đường trung trực của AB.
Mà I là trung điểm của AB
(đpcm)
Áp dụng hệ thức lượng trong vuông tại B có đường cao BI:
(cm)
Câu 54:
Cho (O; 15cm) có dây AB = 24 cm thì khoảng cách từ tâm O đến dây AB là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi H là trung điểm của AB
Xét tam giác AOH vuông tại H có:
(định lý Pytago)
Vậy khoảng cách từ (O) đến dây AB là 9 cm.
Câu 56:
Có 5 học sinh nam là A1, A2, A3, A4, A5 và 3 học sinh nữ là B1, B2, B3 được xếp ngồi xung quanh một bàn tròn. Hỏi có bao nhiêu cách sắp xếp biết A1 không ngồi cạnh B1?
 Xem đáp án
Xem đáp án
Xếp 4 bạn nam (trừ A1) và 2 bạn nữ (trừ B1) thành 1 dãy ta có 6! cách xếp.
Sau đó xếp A1 và B1 vào giữa các bạn đã xếp do A1 và B1 không ngồi cạnh nhau nên ta có 2 trường hợp sau:
TH1: A1 xếp ở đầu nên do khi các bạn ngồi thành bàn tròn thì suy ra B1 không được xếp ở cuối như vậy B1 có 5 cách chọn ⇒ Tương tự với B1 ở đầu ⇒ 6! . 5 . 2 = 7200 cách xếp
TH2: A1, B1 đều không xếp ở đầu hàng ⇒ cách chọn vị trí cho 2 bạn
cách xếp
Suy ra có tất cả 21600 cách xếp.
Câu 57:
Tính biểu thức bằng cách hợp lý:
1 – 2 – 3 + 4 + 5 – 6 – 7 + 8 +… + 997 – 998 – 999 + 1000.
 Xem đáp án
Xem đáp án
1 – 2 – 3 + 4 + 5 – 6 – 7 + 8 +… + 997 – 998 – 999 + 1000
= (1 – 2 – 3 + 4) + (5 – 6 – 7 + 8) +…+ (997 – 998 – 999 + 1000)
= 0 + 0 +…+ 0
= 0.
Câu 58:
Một hình chữ nhật có chu vi 150 m. Nếu giảm chiều dài 10 m và tăng chiều rộng 5m thì được một hình chữ nhật mới có chiều dài gấp 4 lần chiều rộng. Tính diện tích hình chữ nhật ban đầu.
 Xem đáp án
Xem đáp án
Nửa chu vi hình chữ nhật là:
150 : 2 = 75 (m)
Nửa chu vi hình chữ nhật sau khi giảm chiều dài 10m và tăng chiều rộng 5m là:
75 – 10 + 5 = 70 (m)
Tổng số phần bằng nhau là:
4 + 1 = 5 (phần)
Chiều dài hình chữ nhật sau khi giảm là:
70 : 5 × 4 = 56 (m)
Chiều rộng hình chữ nhật sau khi tăng là:
70 – 56 = 14 (m)
Chiều dài hình chữ nhật ban đầu là:
56 + 10 = 66 (m)
Chiều rộng hình chữ nhật lúc đầu là:
14 – 5 = 9 (m)
Diện tích hình chữ nhật là:
66 × 9 = 594 (m2)
Đáp số: 594 m2.
Câu 59:
 Xem đáp án
Xem đáp án
Hiệu của hai số tự nhiên đó là:
5 × 2 + 1 = 11
Số tự nhiên bé cần tìm là:
(2009 – 11 ) : 2 = 999
Số tự nhiên lớn cần tìm là:
999 + 11 = 1020
Đáp số: 1020.
