Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 13)
-
1922 lượt thi
-
56 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Bạn A quét nhà hết 6 giờ, bạn B quét nhà hết 8 giờ. Hỏi nếu hai người cùng làm mất bao nhiêu giờ?
 Xem đáp án
Xem đáp án
Một giờ bạn A làm được là:
1 : 6 = (công việc)
Một giờ bạn B làm được là:
1 : 8 = (công việc)
Một giờ hai bạn làm được:
(công việc)
Thời gian để hai người làm xong công việc là:
(giờ)
Đáp số: giờ.
Câu 2:
Hiện nay, bố hơn con 30 tuổi, biết 5 năm nữa tổng số tuổi của hai bố con là 62. Tính tuổi của mỗi người hiện nay.
 Xem đáp án
Xem đáp án
Vì hiệu số tuổi 2 bố con luôn là 30 tuổi nên khi đó bố hơn con 30 tuổi.
Số tuổi của con 5 năm sau là:
(62 − 30) : 2 = 16 (tuổi)
Số tuổi của bố 5 năm sau là:
16 + 30 = 46 (tuổi)
Số tuổi của con hiện nay là:
16 – 5 = 11 (tuổi)
Số tuổi của bố hiện nay là:
46 – 5 = 41 (tuổi)
Đ/S: bố: 41 tuổi.
con: 11 tuổi.
Câu 3:
Tìm giá trị thích hợp của a sao cho: a00 > –111.
 Xem đáp án
Xem đáp án
Do 100, 200, 300, 400, 500, 600, 700, 800, 900 đều lớn hơn 0 và – 111 < 0.
Nên 100, 200, 300, 400, 500, 600, 700, 800, 900 đều lớn hơn – 111.
⇒ a ∈ {1; 2; 3; 4; 5; 6; 7; 8; 9}.
Câu 4:
Tìm ƯCLN của: 24, 84, 180.
 Xem đáp án
Xem đáp án
84 = 22 ∙ 3 ∙ 7
24 = 23 ∙ 3
180 = 22 ∙ 32 ∙ 5
⇒ ƯCLN (24, 84, 180) = 22 ∙ 3 = 12.
Câu 5:
Trên một cây cầu dài 15 m, người ta trồng những cây trụ làm lan can ở 2 bên cầu. Biết cây này cách cây kia 1,5 m và làm ở cả 2 đầu cầu. Hỏi người ta cần bao nhiêu cây trụ để làm lan can?
 Xem đáp án
Xem đáp án
Số cây trụ một bên cầu:
15 : 1,5 + 1 = 11 (trụ)
Số cây trụ hai bên cầu:
11 × 2 = 22 (trụ)
Đáp số: 22 cây trụ.
Câu 6:
Biết điểm hai bài kiểm tra toán của bạn Anh là điểm 6 và điểm 8. Hỏi điểm bài kiểm tra toán thứ ba của Anh phải là bao nhiêu để điểm trung bình ba bài kiểm tra toán của Anh là điểm 8.
 Xem đáp án
Xem đáp án
Tổng số điểm 3 bài kiểm tra là:
8 × 3 = 24 (điểm)
Điểm bài kiểm tra toán thứ 3 của Anh phải là:
24 − 8 – 6 = 10 (điểm)
Đáp số: 10 điểm.
Câu 7:
 Xem đáp án
Xem đáp án
Gọi số có ba chữ số là (a ∈ ℕ*, b, c ∈ ℕ), xóa chữ số hàng trăm thì được số .
⇒ abc = 7 × bc
100a + 10b + c = 7 × (10b + c)
100a + 10 b + c = 70 b + 7c
100a = 60b + 6c (Trừ cả hai vế của dòng trên đi 10b và c)
50a = 30b + 3c (chia cả hai vế của dòng trên cho 2)
50a = 3 (10b + c) (*)
⇒ 50 a phải chia hết cho 3 ⇒ a chia hết cho 3 (vì số 50 không chia hết cho 3 nên thừa số a phải chia hết cho 3 để tích 50 a chia hết cho 3)
⇒ a = 0 hoặc 3 hoặc 6 hoặc 9
Trường hơp 1: a = 0 (loại vì số abc trở thành số hai chữ số)
Trường hợp 2: a = 3, thay vào (*) ⇒ 50 × 3 = 3 (10b + c)
⇒ 10b + c = 50 ⇒ b và c là thương và dư của phép chia 50 chia cho 10.
Ta có 50 chia 10 được 5 dư 0 ⇒ b = 5, c = 0
⇒ Số cần tìm là 350
Trường hợp 3 : a = 6, thay vào (*) ⇒ 50 × 6 = 3(10b + c)
⇒ 10b + c = 100
Vì b ≤ 9, c ≤ 9 ⇒ 10b + c ≤ 10.9 + 9 = 99 < 100
⇒ Không có chữ số b và c nào thỏa mãn 10b + c = 100
Trường hợp 4: a = 9, cũng lý luận như trường hợp a = 6 ở trên.
Kết luận: Số tìm được là 350.
Câu 9:
Tìm phân số bằng phân số có tử số và mẫu số nhỏ hơn phân số này.
 Xem đáp án
Xem đáp án
Ta coi tử số là 3 phần, mẫu số là 5 phần.
Tử số là: 36 : (5 − 3) × 3 = 54.
Mẫu số là: 54 : 3 × 5 = 90.
Vậy phân số bằng là .
Câu 10:
Trên bàn có một số cái bánh, Dương ăn cái bánh, My ăn cái bánh, Lan ăn cái bánh. Hỏi trên bàn có ít nhất bao nhiêu cái bánh?
 Xem đáp án
Xem đáp án
Trên bàn có ít nhất số cái bánh là:
(cái)
Vì 3 < < 4 nên trên bàn có ít nhất 4 cái bánh.
Đáp số: 4 cái bánh.
Câu 11:
Có một đoàn xe chở gạo lên vùng cao, 4 xe đầu chở được 6 tấn gạo, 3 xe tiếp theo mỗi xe chở 22 tạ gạo và 2 xe cuối, mỗi xe chở 9 tạ gạo. Hỏi trung bình mỗi xe chở được bao nhiêu tạ gạo?
 Xem đáp án
Xem đáp án
Đổi 6 tấn gạo = 60 tạ gạo.
3 xe tiếp theo chở tổng cộng số tạ gạo là:
22 × 3 = 66 (tạ gạo)
2 xe cuối chở tổng cộng số tạ gạo là:
9 × 2 = 18 (tạ gạo)
Đoàn xe chở gạo đó có tổng số xe là:
4 + 3 + 2 = 9 (xe)
Trung bình mỗi xe chở được số tạ gạo là:
(60 + 66 + 18) : 9 = 16 (tạ gạo)
Đ/S: 16 tạ gạo.
Câu 12:
Nhân ngày 20/10 cửa hàng bán túi sách và ví da giảm 30% cho tất cả sản phẩm ai có thẻ VIP giảm 10% trên giá đã giảm.
a) Mẹ bạn An có thẻ VIP thì khi mua 1 cái tui trị giá 500000 đồng phải trả bao nhiêu?
 Xem đáp án
Xem đáp án
a)
Số tiền mẹ bạn An phải trả khi giảm 30% cho túi xách là:
500000 – 500000 ∙ 30% = 350000 (đồng)
Số tiền phải trả khi giảm tiếp 10% là:
350000 – 350000 ∙ 10% = 315000 (đồng)
Vậy khi mua 1 túi xách giá 500000đ thì mẹ An phải trả 315000 đồng
Câu 13:
b) Mẹ bạn mua thêm 1 cái ví nên phải trả tổng cộng là 693000 đồng. Vậy giá bán đầu của cái ví là bao nhiêu?
 Xem đáp án
Xem đáp án
b)
Gọi x (đồng) là giá ban đầu của cái ví (x > 0).
Số tiền phải trả cho cái ví là:
693000 − 315000 = 378000 (đồng)
Số tiền phải trả cho cái ví sau lần giảm 30% là:
x – x ∙ 30% = 0,7x (đồng)
Số tiền phải trả cho cái ví khi giảm tiếp 10% là:
0,7x − 10% ∙ 0,7x = 0,63x (đồng)
Theo đề bài ta có phương trình:
0,63x = 378000
x = 600000 (đồng)
Vậy giá ban đầu của cái ví là 600000 đồng.
Câu 14:
Chứng tỏ rằng: Giá trị của biểu thức
A = 5 + 52 + 53 + ... + 58 là bội của 30.
 Xem đáp án
Xem đáp án
Ta có: A = (5 + 52) + (53 + 54) + (55 + 56) + (57 + 58)
= (5 + 52) + 52(5 + 52) + 54(5 + 52) + 56 (5 + 52)
= 30 + 52 ∙ 30 + 54 ∙ 30 + 56 ∙ 30
= 30 (1 + 52 + 54 + 56) ⋮ 30
Vậy A là bội của 30.
Câu 15:
Đếm số phần tử của các tập hợp:
a. A = {40; 41; 42; .... ;100}
b. B = {10; 12; 14; ....; 98}
c. C = {35; 37; 39; ....; 105}
 Xem đáp án
Xem đáp án
a) Tập hợp Acó số phần tử là:
(100 − 40) : 1 + 1 = 61 (phần tử)
Đáp số: 61 phần tử.
b) Tập hợp B có số phần tử là:
(98 − 10) : 2 + 1 = 45 (phần tử)
Đáp số: 45 phần tử.
c) Tập hợp C có số phần tử là:
(105 − 35) : 2 + 1 = 36 (phần tử)
Đáp số: 36 phần tử.
Câu 16:
Tìm các bội chung có 3 chữ số của 21, 35 và 175.
 Xem đáp án
Xem đáp án
Ta có:
21 = 3 ∙ 7
35 = 5 ∙ 7
175 = 52 ∙ 7
⇒ BCNN (21, 35, 175) = 52 ∙ 3 ∙ 7 = 525
⇒ BC (21, 35, 175) = B (525) = {525; 1050; ...}
Mà BC có 3 chữ số.
⇒ Bội chung có 3 chữ số của 21, 35 và 175 là 525.
Câu 19:
 Xem đáp án
Xem đáp án
S = (1 + 52 + 54 + 56) + ... + (52014 + 52016 + 52018 + 52020)
= (1 + 52 + 54 + 56) + … + 52014 (1 + 52 + 54 + 56)
= (1 + 52 + 54 + 56) (1 + … + 52014)
= 16276 (1 + … + 52014) ⋮ 313 (vì 16276 ⋮ 313)
Vậy S ⋮ 313.
Câu 20:
 Xem đáp án
Xem đáp án
Vì 156 chia cho a dư 12 nên a là ước của 156 − 12 = 144.
Vì 280 chia cho a dư 10 nên a là ước của 280 − 10 = 270.
Vậy a ∈ ƯC(144, 270) và a > 12.
* Ta có: 144 = 24 ∙ 32 và 270 = 2 ∙ 33 ∙ 5
Nên ƯCLN(144, 270) = 2 ∙ 32 = 18
⇒ ƯC (144, 270) = {1; 2; 3; 6; 9; 18}
Kết hợp a > 12 nên a = 18.
Câu 21:
Cho đường tròn (O) đường kính AB. Điểm C di động trên đường tròn, H là hình chiếu của C trên AB. Trên OC lấy M sao cho OM = OH
a, Hỏi điểm M chạy trên đường nào?
 Xem đáp án
Xem đáp án
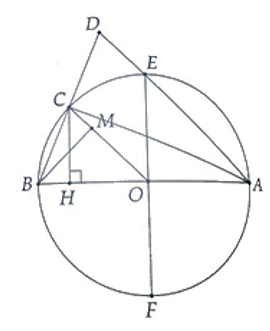
Gọi EF là đường kính (O; ) sao cho EF⊥AB
Xét trường hợp C chạy trên nửa đường tròn EBF
Chứng minh: ∆OMB = ∆OHC (c.g.c)
⇒
Vậy M chạy trên đường tròn đường kính OB.
Chứng minh tương tự khi C chạy trên nửa đường tròn EAF, ta được M chạy trên đường tròn đường kính OA.
Câu 22:
b, Trên tia BC lây điểm D sao cho CD = CB. Hỏi điểm D chạy trên đường nào?
 Xem đáp án
Xem đáp án
Ta có: OC là đường tru ng bình của ∆ABD.
⇒ OC // AD ⇒
Mà (vì ∆OBC cân tại O)
⇒ ⇒ ∆ABD cân tại A
⇒ AD = AB ⇒ D ∈ (A; AB)
⇒ D chạy trên đường tròn tâm A, bán kính AB.
Câu 23:
Một phép trừ có tổng của số bị trừ, số trừ và hiệu là 3864. Hiệu lớn hơn số trừ 36 đơn vị. Tìm số bị trừ, số trừ, hiệu.
 Xem đáp án
Xem đáp án
Vì Số bị trừ (SBT) = Số trừ (ST) + Hiệu (H) nên SBT + ST + H = SBT × 2.
Số bị trừ là: 3864 : 2 = 1932
Số trừ là: (1932 − 36) : 2 = 948
Hiệu là: 948 + 36 = 984
Đáp số: SBT: 1932; ST: 948; H: 984.
Câu 24:
Một phép trừ có tổng của số bị trừ, số trừ và hiệu là 7652. Hiệu lớn hơn số trừ 798 đơn vị. Hãy tìm phép trừ đó?
 Xem đáp án
Xem đáp án
Số bị trừ là:
7652 : 2 = 3826
Tổng của số trừ và hiệu bằng số bị trừ và bằng 3826.
Hiệu là:
(3826 + 798) : 2 = 2312
Số trừ là:
3826 – 2312 = 1514
Vậy phép trừ đó là: 3826 – 2312 = 1514.
Câu 25:
Một sân phơi có diện tích 44 m2. Chiều rộng bằng m. Hỏi chu vi sân phơi là bao nhiêu mét?
 Xem đáp án
Xem đáp án
Chiều dài sân phơi là:
Chu vi sân phơi là:
Đáp số: m.
Câu 26:
Người ta dùng gạch men để lát một căn phòng hình chữ nhật có chiều dài 9 m, chiều rộng 8 m. Hỏi cần bao nhiêu tiền mua gạch để lát kín nền căn phòng đó, biết giá tiền một mét vuông gạch men là 90 000 đồng. Diện tích phần mạch vữa không đáng kể.
 Xem đáp án
Xem đáp án
Diện tích căn phòng là:
9 × 8 = 72 (m2)
Cần số tiền để mua gạch lát kín nền căn phòng đó là:
90000 × 72 = 6480000 (đồng)
Đáp số: 6 480 000 đồng.
Câu 27:
Một bạn viết liên tiếp nhóm chữ GIAIPHONGMIENNAM thành dãy GIAIPHONGMIENNAMGIAIPHONGMIENNAM ...
a, Chữ cái thứ 1975 là gì?
 Xem đáp án
Xem đáp án
a)
Mỗi nhóm chữ GIAIPHONGMIENNAM có 16 chữ cái mà 1975 : 16 = 123 dư 7
Vậy với 1975 chữ cái sẽ viết được 123 nhóm chữ và dư 7 chữ cái. Với 7 chữ cái này ta lần lượt viết đến chữ cái thứ bảy từ trái sang của GIAIPHONGMIENNAM đó là chữ O.
Câu 28:
b, Người ta tô các chữ cái trong dãy theo thứ tự Xanh, Đỏ, Tím, Vàng, Xanh, Đỏ, Tím, Vàng ... Chữ cái thứ 2015 màu gì?
 Xem đáp án
Xem đáp án
b)
Cứ 4 màu xanh, đỏ, tím, vàng tạo thành 1 nhóm có 4 màu.
Mà 2015 : 4 = 503 dư 3
Vậy lập được 5013 nhóm chữ đủ cả 4 màu. Còn thừa 3 màu tô, do đó chữ cái thứ 2015 được tô màu tím.
Câu 29:
Một người viết liên tiếp nhóm chữ Tổ quốc Việt Nam thành dãy
Tổ quốc Việt Nam Tổ quốc Việt Nam ...
Người ta tô màu các chữ cái trong dãy theo thứ tự: xanh, đỏ, tím, vàng, xanh, đỏ, ... Hỏi chữ cái thứ 1995 trong dãy tô màu gì?
 Xem đáp án
Xem đáp án
Ta nhận xét: các màu xanh, đỏ, tím, vàng gồm có 4 màu.
Mà 1995 : 4 = 498 (nhóm) dư 3.
Những chữ cái trong dãy có số thứ tự là số chia cho 4 dư 3 thì được tô màu tím.
Vậy chữ cái thứ 1995 trong dãy được tô màu tím.
Câu 30:
Nhà trường mở rộng hình vuông về 4 cả phía, mỗi phía thêm 3m điện tích tăng thêm 336m2. Tính chu vi khu vườn sau khi mở rộng?
 Xem đáp án
Xem đáp án
Khu vườn tăng thêm số m là:
3 × 4 = 12 (m)
Cạch khu vườn sau khi mở rộng là:
336 : 12 = 28 (m)
Chu vi hình khu vườn sau khi mở rộng là:
28 × 4 = 112 (m)
Đáp số: 112 m.
Câu 31:
Sông Nin ở Châu Phi dài 6732km, sông Mê Kông ở Châu Á dài 4183km. Hỏi sông nào dài hơn và dài hơn bao nhiêu ki – lô – mét?
 Xem đáp án
Xem đáp án
Vì 6732 km > 4183 km nên sông Nin dài hơn sông Mê Kông.
Sông Nin ở Châu Phi dài hơn và dài hơn số ki–lô–mét là:
6732 – 4183 = 2549 (km)
Đáp số: 2549 km.
Câu 32:
Trên một bản đồ tỉ lệ 1 : 1000 có hình vẽ một khu đất hình chữ nhật với chiều dài 6 cm và chiều rộng 4 cm. Tính diện tích khu đất đó bằng đơn vị ha.
 Xem đáp án
Xem đáp án
Chiều dài thật khu đất đó là:
6 × 1000 = 6000 (cm)
Chiều rộng thật khu đất đó là:
4 × 1000 = 4000 (cm)
Diện tích khu đất đó là :
6000 × 4000 = 24 000 000 (cm2)
Đổi : 24 000 000 cm2 = 0,24 ha.
Đáp số: 0,24 ha.
Câu 33:
Tìm hai số có hiệu bằng 16, biết rằng nếu lấy số thứ nhất cộng số thứ hai rồi cộng tổng của chúng thì được 160.
 Xem đáp án
Xem đáp án
Vì tổng bằng số thứ nhất cộng số thứ hai nên số thứ nhất cộng số thứ hai cộng tổng chính là 2 lần tổng 2 số.
Tổng 2 số là:
160 : 2 = 80
Số bé là :
(80 − 16) : 2 = 32
Số lớn là :
32 + 16 = 48
Đáp số: 32,48.
Câu 34:
Tìm hai số có hiệu bằng 644, biết rằng nếu lấy số thứ nhất cộng với số thứ hai rồi cộng với tổng của chúng thì được 2584.
 Xem đáp án
Xem đáp án
Tổng của 2 số là:
2584 : 2 = 1292
Số bé là :
(1292 − 644) : 2 = 325
Số lớn là :
325 + 644 = 969
Đáp số : Số bé: 325
Số lớn: 969.
Câu 35:
Tính tổng các chữ số của A, biết rằng: (có 100 chữ số 9).
 Xem đáp án
Xem đáp án
Tổng các chữ số của A bằng 900 + 2 + 1 + 6 = 909.
Câu 36:
Tính tổng của số lớn nhất có năm chữ số và số bé nhất có năm chữ số khác nhau.
 Xem đáp án
Xem đáp án
Ta có: Số lớn nhất có năm chữ số là: 99999
Số bé nhất có năm chữ số khác nhau là: 10234
Tổng của số lớn nhất có năm chữ số và số bé nhất có năm chữ số khác nhau là:
10234 + 99999 = 110233
Đáp số: 110233.
Câu 37:
Sắp xếp các phân số sau theo thứ tự từ bé đến lớn: .
 Xem đáp án
Xem đáp án
Thứ tự từ bé đến lớn của các phân số là: .
Câu 38:
Một phép nhân có hai thừa số, thừa số thứ nhất bằng 6, tích bằng 66. Hỏi thừa số thứ hai bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Thừa số thứ hai là 66 : 6 = 11.
Đáp số: thừa số thứ hai là 11.
Câu 40:
Cho x, y, z là số thực dương khác 0 thỏa mãn:
. Chứng minh rằng .
 Xem đáp án
Xem đáp án
Ta có:
Lại có: x3 + y3 + z3 − 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)
⇒ x3 + y3 + z3 − 3xyz = 0
⇒ x3 + y3 + z3 = 3xyz.
Câu 42:
Chứng minh mệnh đề sau bằng phản chứng:
Nếu a.b chia hết cho 7 thì a hoặc b chia hết cho 7.
 Xem đáp án
Xem đáp án
Lời giải:
Nếu cả 2 số không chia hết cho 7
⇒ a không chia hết cho 7, b không chia hết cho 7
⇒ a.b không chia hết cho 7 (trái với đề bài)
vậy 1 trong 2 số a và b phải chia hết cho 7.
Câu 43:
Biết a + b chia hết cho 7. Chứng minh rằng chia hết cho 7.
 Xem đáp án
Xem đáp án
Có = 100a + 10b + a = 101a + 10b = 91a + 10(a + b)
Vì 91 chia hết cho 7 nên 91a chia hết cho 7 (1)
Lại có: a + b chia hết cho 7 nên 10(a + b) chia hết cho 7 (2)
Từ (1) và (2) ⇒ ⋮ 7.
Câu 44:
Cho tam giác ABC nhọn, đường cao BD và CE. Lấy điểm M thuộc BD sao cho góc AMC = 90°, lấy điểm N thuộc đoạn CE sao cho góc ANB = 90°.
Chứng minh tam giác AMN cân.
 Xem đáp án
Xem đáp án
Áp dụng HTL tam giác AMC vuông tại M và ANB vuông tại N có:
(1)
Vì
Câu 45:
Chứng minh rằng trong một tam giác trung tuyến ứng với cạnh lớn hơn thì nhỏ hơn trung tuyến ứng với cạnh nhỏ.
 Xem đáp án
Xem đáp án
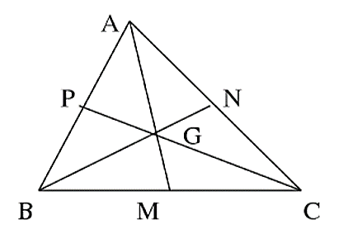
Xét tam giác ABC các đường trung tuyến AM, BN, CP trọng tâm G.
Giả sử AB < AC
Ta cần đi chứng minh CP > BN
Xét hai tam giác ABM và ACM ta có:
MB = MC (vì M là trung điểm của BC)
AM chung: AB < AC do đó: M1 < M2.
Với hai tam giác GBM và GCM ta có: MB = MC (M là TĐ của BC); GM chung.
Do đó: GB < GC ⇔
Câu 46:
Lan có nhiều hơn Hồng 12 quyển truyện nhi đồng. Nếu Hồng mua thêm 8 quyển và Lan mua thêm 2 quyển thì hai bạn có tổng cộng 46 quyển. Hỏi mỗi bạn có bao nhiêu quyển truyện nhi đồng ?
 Xem đáp án
Xem đáp án
Trước khi mua thêm 2 bạn có tất cả số truyện là:
46 − 8 − 2 = 36 (quyển)
Lan có số quyển truyện là:
(36 + 12) : 2 = 24 (quyển)
Hồng có số quyển truyện là:
24 − 12 = 12 (quyển)
Câu 47:
Hà có nhiều hơn Mai 16 quyển truyện. Nếu mai mua thêm 10 quyển và Hà mua thêm 4 quyển thì 2 bạn có tổng cộng 50 quyển. Hỏi mỗi bạn có bao nhiêu quyển truyện.
 Xem đáp án
Xem đáp án
Hiệu số quyển của Hà và Mai là 16 quyển.
Tổng số quyển của Hà và Mai cộng lại là:
50 − (10 + 4) = 36 (quyển)
Số quyển vở của Mai là:
(36 −16) : 2 = 10 (quyển)
Số quyển vở của Hà là:
36 − 10 = 26 (quyển)
Đáp số: Hà: 26 quyển.
Mai: 10 quyển.
Câu 48:
Lớp 4A quyên góp được 86 quyển vở, lớp 4B quyên góp được 100 quyển vở, lớp 4C quyên góp được ít hơn tổng số vở của hai lớp 4A và 4B là 42 quyển. Hỏi trung bình mỗi lớp quyên góp được bao nhiêu quyển vở?
 Xem đáp án
Xem đáp án
Tổng số vở lớp 4A và lớp 4B quyên góp được là:
86 + 100 = 186 (quyển vở)
Số vở lớp 4C quyên góp được là:
186 – 42 = 144 (quyển vở)
Trung bình mỗi lớp quyên góp được số quyển vở là:
(186 + 144) : 3 = 110 (quyển vở)
Đáp số: 110 quyển vở.
Câu 49:
Lớp 4A quyên góp được 33 quyển vở, lớp 4B được 28 quyển vở, lớp 4C nhiều hơn lớp 4B 7 quyển vở. Hỏi trung bình mỗi lớp quyên góp được mấy quyển vở?
 Xem đáp án
Xem đáp án
Lớp 4C quyên góp được số vở là:
28 + 7 = 35 (quyển)
Cả 3 lớp quyên góp được số vở là:
33 + 28 + 35 = 96 (quyển)
Trung bình mỗi lớp quyên góp được số vở là:
96 : 3 = 32 ( quyển)
Đáp số: 32 quyển.
Câu 50:
Một hình chữ nhật nếu giảm chiều dài 5m và tăng chiều rộng 5m thì ta được hình vuông có chu vi 164m. Tính chu vi hình chữ nhật?
 Xem đáp án
Xem đáp án
Khi giảm chiều dài đi 5m và tăng chiều rộng 5m thì thành hình vuông nghĩa là lúc đó thì chiều dài bằng chiều rộng.
Chiều dài là : (164 : 4) + 5 = 46 (m)
Chiều rộng là : (164 : 4) − 5 = 36 (m)
Chu vi là : (46 + 36) ∙ 2 = 164 (m)
Đáp số: Chu vi hình chữ nhật là 164 m.
Câu 51:
Một mảnh đất hình chữ có chu vi là 180m chiều dài hơn chiều rộng 22m.
a, Tính chiều dài và chiều rộng.
 Xem đáp án
Xem đáp án
a)
Nửa chu vi mảnh đất hình chữ nhật hay tổng chiều dài và chiều rộng của hình chữ nhật là:
180 : 2 = 90 (m)
Chiều rộng của mảnh đất hình chữ nhật là:
(90 − 22) : 2 = 34 (m)
Chiều dài của mảnh đất hình chữ nhật là:
34 + 22 = 56 (m)
Câu 52:
b, Tính diện tích của mảnh đất đó.
 Xem đáp án
Xem đáp án
b)
Diện tích của mảnh đất hình chữ nhật là:
34 × 56 = 1904 (m2)
Đáp số: a) 34 m và 56 m.
b) 1904 m2.
Câu 53:
Tìm một số có hai chữ số, biết rằng nếu viết thêm chữ số 6 vào bên trái của số đó thì được số mới gấp 9 lần số phải tìm.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là ab với a; b là chữ số.
Nếu viết thêm chữ số 6 vào bên trái của số đó thì số đó tăng 600
9 ∙ ab = 600 + ab
8 ∙ ab = 600
ab = 600 : 8
ab = 75
Vậy số cần tìm là 75.
Câu 54:
 Xem đáp án
Xem đáp án
Vì 156 chia cho a dư 12 nên a là ước của 156 − 12 = 144.
Vì 280 chia cho a dư 10 nên a là ước của 280 − 10 = 270.
Vậy a ∈ ƯC(144, 270) và a > 12.
* Ta có: 144 = 24∙32 và 270 = 2∙33∙5
Nên ƯCLN (144; 270) = 2 ∙ 32 = 18
⇒ ƯC(144; 270) = {1; 2; 3; 6; 9; 18}
Kết hợp a > 12 nên a = 18.
Câu 56:
Hãy tìm tập hợp Ư (105), Ư (140) và ƯC (105, 140).
 Xem đáp án
Xem đáp án
Ư(105) = {1; 3; 5; 7; 15; 21; 35; 105}
Ư(140) = {1; 2; 4; 5; 7; 10; 14; 20; 28; 35; 70; 140}
ƯC(105; 140) = {5; 7; 35}
Bội chung của 10 và 12
Ta có: 10 = 2 ∙ 5
12 = 22 ∙ 3
Bội chung là: 22 ∙ 3 ∙ 5 = 60.
