Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 22)
-
2103 lượt thi
-
60 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC vuông tại A có AB < AC. Gọi D và E lần lượt là trung điểm của các cạnh AC và BC, kẻ EF ⊥ AB tại F.
a) Chứng minh ADEF là hình chữ nhật.
 Xem đáp án
Xem đáp án
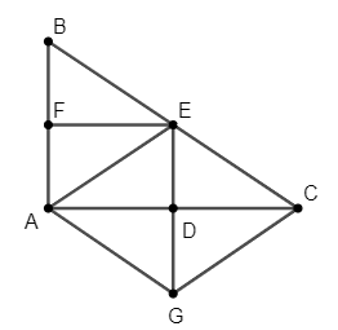
a) Xét ∆ABC, có:
DA = DC (gt))
EB = EC (gt)
Suy ra DE là đường trung bình của ∆ABC.
Do đó DE // AB
Mà AB AC (gt)
Suy ra DE AC
Xét tứ giác ADEF có:
Suy ra tứ giác ADEF là hình chữ nhật.
Câu 2:
b) Gọi G là điểm đối xứng với E qua D. Chứng minh tứ giác AECG là hình thoi.
 Xem đáp án
Xem đáp án
b) Xét tứ giác AECG, có:
AC∩EG = {D}
DA = DC (gt)
DG = DE (gt)
Suy ra tứ giác AECG là hình bình hành.
Mà DE AC (cmt)
Suy ra tứ giác AECG là hình thoi.
Câu 3:
Cho ∆ABC vuông tại A, có . Gọi M và N lần lượt là trung điểm của BC và AC.
a) Tính .
 Xem đáp án
Xem đáp án
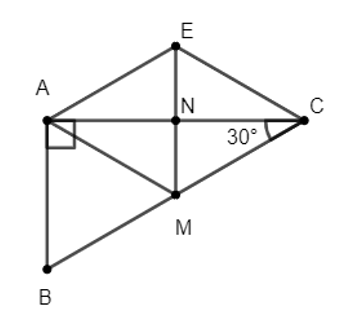
a) Xét ∆ABC có:
M, N lần lượt là trung điểm của AC và BC.
Suy ra MN là đường trung bình của ∆ABC.
Do đó MN // AB
Mà AB AC nên AC MN hay
= 180° – 90° – 30° = 60°
Câu 4:
 Xem đáp án
Xem đáp án
b) Xét tứ giác AECM, có:
AC cắt EM tại N
NA = NC (gt)
NG = NE (gt)
Suy ra tứ giác AECM là hình bình hành.
Mà MN ⊥ AC (cmt)
Suy ra tứ giác AECM là hình thoi.
Câu 5:
Cho tam giác ABC. Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho NA = 2NC. Gọi K là trung điểm của MN.
Phân tích theo và .
 Xem đáp án
Xem đáp án
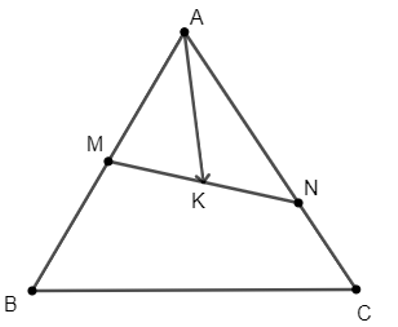
Vì M là trung điểm của MN nên ta có:
Vậy .
Câu 6:
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC (H ∈ BC). Cho biết
AB = 13 cm, AH = 12 cm, HC = 16 cm. Tính độ dài các cạnh AC, BC.
 Xem đáp án
Xem đáp án
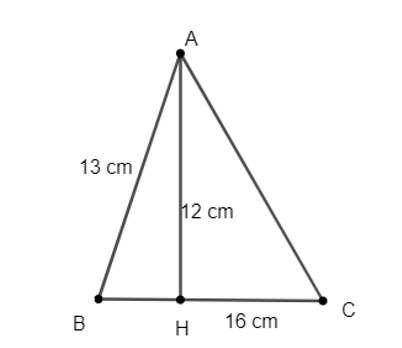
Xét ∆AHC vuông tại H nên ta có:
AC2 = AH2 + HC2
= 20 (cm)
Xét ∆AHC vuông tại H nên ta có:
AB2 = AH2 + BH2
= 5 (cm)
BC = BH + HC = 5 + 16 = 21 (cm)
Vậy AC = 20 cm, BC = 21 cm.
Câu 7:
Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB tới đường tròn (O) với A, B là các tiếp điểm.
a) Chứng minh bốn điểm A, B, M, O cùng thuộc một đường tròn.
 Xem đáp án
Xem đáp án
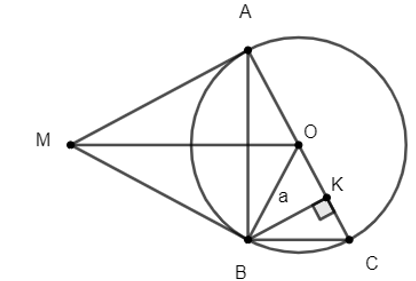
a) Xét tứ giác AOBM có:
Do đó tứ giác AOBM là tứ giác nội tiếp đường tròn.
Vậy bốn điểm A, B, M, O cùng thuộc một đường tròn.
Câu 8:
b) Kẻ đường kính AC của đường tròn (O). Chứng minh OM // CB.
 Xem đáp án
Xem đáp án
b) Theo tính chất 2 tiếp tuyến cắt nhau ta có:
MA = MB.
Lại có OA = OB = R
Suy ra OM là đường trung trực của đoạn thẳng AB.
OM AB
Mà (do góc nội tiết chắn nửa đường tròn)
AB BC
Từ (1) và (2) OM//BC
Câu 9:
 Xem đáp án
Xem đáp án
c) Do OM//BC (hai góc ở vị trí đồng vị)
Lại có OM là đường trung trực trong ∆OAB cân nên nó cũng là đường phân giác của ∆OAB
Nên suy ra
Xét ∆BCK và ∆MOB có:
(cmt)
(g.g)
CK.OM = OB.CB (đpcm)
Câu 10:
Tính (72014 + 72012) : 72012.
 Xem đáp án
Xem đáp án
(72014 + 72012) : 72012
= 72014 : 72012 + 72012 : 72012
= 72014 – 2012 + 72012 – 2012
= 72 + 70
= 49 + 1
= 50
Câu 11:
Tìm chữ số tận cùng của 799.
 Xem đáp án
Xem đáp án
5 lần 7 nhân với nhau có tận cùng là 7, có số nhóm như vậy:
99 : 5 = 19 (dư 4)
Đang có tận cùng là 7 nhân thêm 1 số 7 nữa có tận cùng là 9.
Đang có tận cùng là 9 nhân thêm 1 số 7 nữa có tận cùng là 3.
Đang có tận cùng là 3 nhân thêm 1 số 7 nữa có tận cùng là 1.
Vậy tận cùng của 799 là 1.
Câu 12:
Từ điểm I nằm ngoài đường tròn (O), vẽ cát tuyến cắt đường tròn tại A và B (IA < IB). Các tiếp tuyến tại A và B cắt nhau tại M. OM cắt AB tại K.
a) Chứng minh K là trung điểm của AB.
 Xem đáp án
Xem đáp án

a) Ta có MA, MB là hai tiếp tuyến của (O) cắt nhau tại M.
Suy ra MA = MB.
Khi đó M nằm trên đường trung trực của đoạn thẳng AB (1)
Lại có OA = OB = R.
Suy ra O nằm trên đường trung trực của đoạn thẳng AB (2)
Từ (1), (2), suy ra MO là đường trung trực của đoạn thẳng AB.
Do đó MO ⊥ AB tại K và K là trung điểm AB.
Câu 13:
b) Vẽ MH ⊥ OI tại H. Chứng minh OB2 = OH.OI.
 Xem đáp án
Xem đáp án
b) Xét ∆OHM và ∆OKI, có:
chung.
Do đó (g.g)
Do đó OH.OI = OM.OK (1)
Xét ∆AOM vuông tại A có AK là đường cao.
OA2 = OK.OM (hệ thức lượng trong tam giác vuông) (2)
Từ (1) và (2) suy ra OH.OI = OA2 = OB2 (đpcm)
Câu 14:
Một hình bình hành ABCD có diện tích 350 cm2, biết độ dài đường cao AH = 35 cm. Tính độ dài cạnh AB.
 Xem đáp án
Xem đáp án
Ta có diện tích của hình bình hành là:
SABCD = AH.AB
35.AB = 350
(cm)
Vậy AB = 10 cm.
Câu 15:
Chứng minh rằng:
Nếu p và p2 + 8 là hai số nguyên tố thì p2 + 2 cũng là số nguyên tố.
 Xem đáp án
Xem đáp án
Với Xét với p = 3k + 1 (k nguyên) thì p2 + 8 3, là một hợp số.
Xét p = 3k + 2 thì p2 + 8 3, là hợp số.
Vậy p = 3k, mà p là số nguyên tố nên p = 3.
Khi đó p2 + 2 = 11, là số nguyên tố.
đpcm.
Câu 16:
Chứng minh rằng. nếu p và 8p2 + 1 là hai số nguyên tố lẻ thì 8p2 + 2p + 1 là số nguyên tố.
 Xem đáp án
Xem đáp án
Do p là số nguyên tố lẻ nen p = 3k ± 1 hoặc p = 3k
Nếu p = 3k ± 1 thì
8p2 + 1 = 8(3k ± 1)2 + 1 = 3(24k2 ± 16k + 3) 3, là một hợp số (loại)
Nếu p = 3k do p là số nguyên nên p = 3
Khi đó 8p2 + 1 = 8.9 + 1 =73 là số nguyên tố,
8p2 + 2p + 1 = 72 + 6 + 1 = 791 là một số nguyên tố.
Vậy ta có điều phải chứng minh.
Câu 17:
Tìm tất cả các cặp số nguyên (x, y) thỏa mãn (x – 1)2 + 5y2 = 6.
 Xem đáp án
Xem đáp án
Ta có: (x – 1)2 + 5y2 = 6
Vậy (x, y) ∈ {(2; 1); (2; −1); (0; 1); (0; −1)}.
Câu 18:
 Xem đáp án
Xem đáp án
x(y – 1) + y = 2
⇔ x(y – 1) + (y – 1) = 2 – 1
⇔ (y – 1)(x + 1) = 1
Vậy (x; y) ∈ {(0; 2), (0; −2)}
Câu 19:
Tìm x:
a) 2(x – 5) – 3(x + 7) = 14;
b) 5(x – 6) – 2(x + 3) = 12;
 Xem đáp án
Xem đáp án
a) 2(x – 5) – 3(x + 7) = 14
2x – 10 – 3x – 21 = 14
−x = 14 + 31
x = −45
Vậy x = −45
b) 5(x – 6) – 2(x + 3) = 12
5x – 30 – 2x – 6 = 12
3x = 12 + 36
3x = 48
x = 16
Vậy x = 16.
Câu 20:
Tìm x:
c) −7(3x – 5) + 2(7x – 14) = 28;
d) 5(3 – 2x) + 5(x – 4) = 6 – 4x.
 Xem đáp án
Xem đáp án
c) −7(3x – 5) + 2(7x – 14) = 28
−21x + 35 + 14x – 28 = 28
−7x = 28 – 7
−7x = 21
x = −3
Vậy x = −3
d) 5(3 – 2x) + 5(x – 4) = 6 – 4x
15 – 10x + 5x – 20 = 6 – 4x
−5x + 4x = 6 + 5
−x = 11
x = −11
Vậy x = −11
Câu 21:
Tìm x:
a) −5(2 – x) + 4(x – 3) = 10x – 15 Xem đáp án
Xem đáp án
a) −5(2 – x) + 4(x – 3) = 10x – 15
−10 + 5x + 4x – 12 = 10x – 15
9x – 22 = 10x – 15
10x – 9x = 15 – 22
x= −7
Vậy x = −7
Câu 22:
Tìm x:
b) 2(4x – 8) – 7(3 + x) = |−4|(3 – 2);
 Xem đáp án
Xem đáp án
b) 2(4x – 8) – 7(3 + x) = |−4|(3 – 2)
8x – 16 – 21 – 7x = 4
x – 37 = 4
x = 41
Vậy x = 41
Câu 23:
Tìm x:
c) 8(x – |−7|) – 6(x – 2) = |−8|.6 – 50.
 Xem đáp án
Xem đáp án
c) 8(x – |−7|) – 6(x – 2) = |−8|.6 – 50
8x – 56 – 6x + 12 = 48 – 50
2x = −2 + 44
2x = 42
x = 21
Vậy x = 21
Câu 24:
Tìm m để bất phương trình x2 – 2(m + 1) + m2 + 2m ≤ 0 có nghiệm với mọi m ∈ [0; 1].
 Xem đáp án
Xem đáp án
Đặt x2 – 2(m + 1) + m2 + 2m = f(x)
Bất phương trình có nghiệm đúng với x ∈ [0; 1]
Phương trình f(x) = 0 có hai nghiệm thỏa mãn
x1 ≤ 1 < 2 ≤ x2 ⇔
Vậy với −1 ≤ m ≤ 0 thỏa mãn yêu cầu bài toán.
Câu 25:
Cho phương trình x2 – 2(m – 1)x + 2m – 5 = 0.
a) Chứng minh phương trình trên luôn có 2 nghiệm phân biệt x1; x2 với mọi m.
 Xem đáp án
Xem đáp án
a) Ta có:
∆’ = (m – 1)2 – (2m – 5)
= m2 – 2m + 1 – 2m + 5
= m2 – 4m + 6
= m2 – 2m.2 + 4 + 2
= (m – 2)2 + 2 > 0 x ∈ ℝ.
Suy ra phương trình đã cho luôn có hai nghiệm phân biệt x1; x2.
Câu 26:
 Xem đáp án
Xem đáp án
b) Theo định lý Vi-ét ta có:
Mà x1 + x2 = 6
2(m – 1) = 6
⇔ m – 1= 3
⇔ m = 4.
Vậy với m = 4 thì thỏa mãn yêu cầu bài toán.
Câu 27:
Xác định Parabol y = ax2 + bx + c, biết parabol có đỉnh nằm trên trục hoành và đi qua hai điểm A(0; 1) và B(2; 1).
 Xem đáp án
Xem đáp án
Do đồ thị hàm số (P) đi qua A nên ta có c = 1.
(P) có đỉnh nằm trên trục hoành nên:
⇔ b2 – 4ac = 0
⇔ b2 = 4ac = 4a
(1)
Do đồ thị hàm số (P) đi qau B(2; 1) nên:
4a + 2b + c = 1
⇔ 4a + 2b = 0
Thay (1) vào ta có:
b2 + 2b = 0
Với b = 0 suy ra a = 0 (loại)
Với b = −2 suy ra a = 1 (thỏa mãn)
Vậy phương trình cần tìm là: y = x2 – 2x + 1.
Câu 29:
Cho a là góc tù và . Tính giá trị của biểu thức:
A = 2sina − cosa.
 Xem đáp án
Xem đáp án
Ta có: sin2a + cos2a = 1
⇔ cos2a = 1 – sin2a
Mà a là góc tù nên cosa < 0
Khi đó: A = 2sina − cosa
Vậy .
Câu 30:
Cho đa thức P(x) = x4 – 4x2 + 5 – 2x. Tìm đa thức Q(x) sao cho
P(x) + Q(x) = 2x2 + 4x – 3.
 Xem đáp án
Xem đáp án
Ta có: P(x) + Q(x) = 2x2 + 4x – 3.
⇔ Q(x) = 2x2 + 4x – 3 – (x4 – 4x2 + 5 – 2x) = −x4 + 6x2 + 6x – 8.
Vậy Q(x) = −x4 + 6x2 + 6x – 8.
Câu 31:
Đa thức P(x) bậc 4 có hệ số bậc cao nhất là 1. Biết P(1) = 0; P(3) = 0;
P(5) = 0. Hãy tính giá trị của biểu thức Q = P(−2) + 7P(6).
 Xem đáp án
Xem đáp án
P(1) = 0; P(3) = 0; P(5) = 0 nên 1 ; 3 ; 5 lần lượt là nghiệm của phương trình nên
P(x) chứa nhân tử (x – 1); (x – 3); (x – 5)
Vì P(x) bậc 4 có hệ số bậc cao nhất là một nên P(x) có dạng:
P(x) = (x – 1)(x – 3)(x – 5)(x – a)
Q = P(–2) + 7P(6)
= (–2 – 1)( –2 – 3)( –2 – 5)( –2 – a) + 7(6 – 1)(6 – 3)(6 – 5)(6 – a)
= 210 + 105a + 7(90 - 15a)
= 210 + 105a + 630 - 105a
= 840
Câu 32:
 Xem đáp án
Xem đáp án
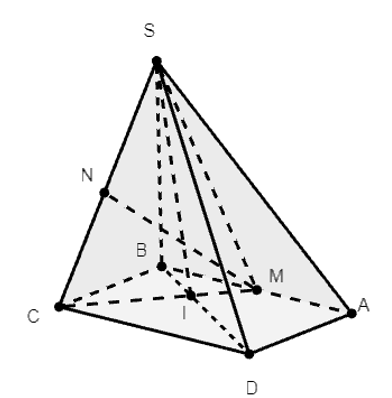
Ta có: M ∈ SM, N ∈ SC, SM ∩ SC = {S}
⇒ MN ∈ (SMC)
Gọi BD ∩ MC = {I}
⇒ I ∈ (SMC)
I ∈ BD, BD ∈ (SBD)
⇒ I ∈ (SBD)
Ta thấy: (SBD) và (SMC) có chung điểm S, BD ∩ MC = {I}
⇒ SI là giao tuyến của (SBD) và (SMC)
Hay SI là giao tuyến của (SBD) và (SMN).
Câu 33:
Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC.
a) Chứng minh tứ giác BHEK là tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
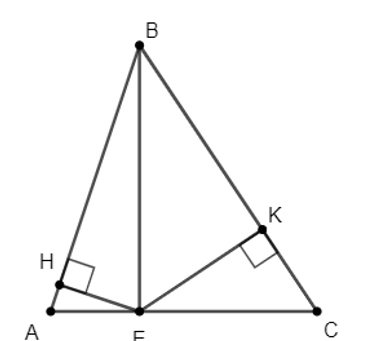
a) Vì EH AB tại H hay
Vì EK BC tại K hay
Xét tứ giác BHEK có:
⇒ Tứ giác BHEK nội tiếp đường tròn.
Câu 34:
b) Chứng minh: BH.BA = BK.BC.
 Xem đáp án
Xem đáp án
b) Xét ∆AEB vuông tại E có EH là đường cao
⇒ BH.BA = BE2
Tương tự BK.BC = BE2
⇒ BH.BA = BK.BC (đpcm)
Câu 35:
Cho đường tròn (O; R) đường kính AB. Điểm C thuộc đường tròn sao cho AC > CB, C khác A và B. Kẻ CH vuông góc với AB tại H; kẻ OI vuông góc với AC tại I.
a) Chứng minh 4 điểm C, H, O, I cùng thuộc một đường tròn.
 Xem đáp án
Xem đáp án
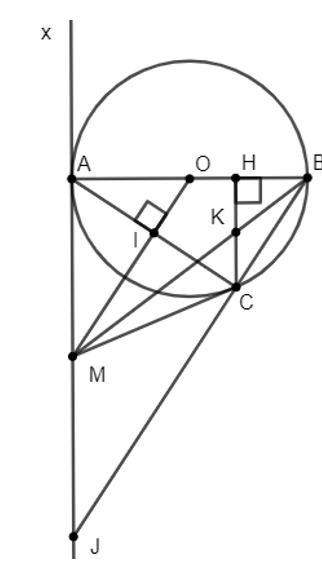
a) Xét tứ giác CIOH có:
Suy ra tứ giác CIOH nội tiếp đường tròn hay 4 điểm C; I; O; H nằm trên một đường tròn.
Câu 36:
b) Kẻ tiếp tuyến Ax của đường tròn (O; R), tia OI cắt Ax tại M, chứng minh
 Xem đáp án
Xem đáp án
b) Xét ∆MAO có vuông tại A có AI MO
⇒ OM.OI = AO2 = R2
Câu 37:
Có một ca 1 l và một ca 300 ml. Chỉ dùng hai ca đó, làm thế nào để lấy được 400 ml từ xô nước.
 Xem đáp án
Xem đáp án
Lấy 1 l nước từ xô nước
Tiến hành đổ nước từ ca 1l vào ca 300 ml hai lần (cả hai lần đã đổ đi 600 ml nước)
Lượng nước còn lại trong ca 1 l khi đó sẽ còn 400 ml.
Câu 38:
Liệt kê các số chẵn từ 0 đến 98.
 Xem đáp án
Xem đáp án
Các số chẵn từ 0 đến 98:
0; 2; 4; 6; 8;…; 96; 98.
Quy luật số liền sau cách số liền trước hai đơn vị.
Câu 39:
Một trường phổ thông có 3 lớp 7, tổng số học sinh của 2 lớp 7A và 7B là 85 học sinh. Nếu chuyển 10 học sinh 7A sang 7C thì số học sinh 3 lớp tỉ lệ thuận là 7; 8; 9. Tính số học sinh của mỗi lớp.
 Xem đáp án
Xem đáp án
Gọi số học sinh 3 lớp A, B, C lần lượt là: a, b, c (học sinh, a,b,c ∈ ℕ*)
Ta có:
a + b = 85 ⇔ (a – 10) + b = 75.
Theo bài cho ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Khi đó:
a – 10 = 5.7 ⇒ a = 45
b = 5.8 = 40
c +10 = 9.5 ⇒ c = 35
Đáp số: Lớp 7A có 45 học sinh.
Lớp 7B có 40 học sinh.
Lớp 7C có 35 học sinh.
Câu 40:
Một lớp có 7 học sinh giỏi Toán, 5 học sinh giỏi Văn, 6 học sinh giỏi Lịch Sử. Hỏi có bao nhiêu cách chọn ra
a) 3 học sinh giỏi?
 Xem đáp án
Xem đáp án
a) Số cách chọn số học sinh giỏi là:
(cách chọn)
Câu 41:
b) 3 học sinh giỏi trong đó có tất cả học sinh giỏi của cả 3 môn?
c) 2 học sinh giỏi ở hai bộ môn khác nhau?
 Xem đáp án
Xem đáp án
b) Số cách chọn 3 học sinh giỏi trong đó có tất cả học sinh giỏi của cả 3 môn là:
7.5.6 = 210 (cách)
c) Số cách chọn 2 học sinh giỏi ở hai bộ môn khác nhau là:
7.5 + 5.6 + 7.6 = 107 (cách)
Câu 42:
Giải phương trình:
log2x + log3x + log4x = log20x
 Xem đáp án
Xem đáp án
Điều kiện: x > 0
Ta có:
log2x + log3x + log4x = log20x
⇔ log2x = 0
⇔ x = 1 (thỏa mãn)
Vậy phương trình đã cho có nghiệm duy nhất x = 1.
Câu 43:
Cho tam giác ABC có: AB = 25 cm; BC = 36 cm; AC = 24 cm. Tính số đo góc C.
 Xem đáp án
Xem đáp án
Theo định lí cosin ta có:
AB2 = AC2 + BC2 – 2AC.BC.cos
Vậy .
Câu 44:
Cho hình bình hành ABCD.
a) Chứng minh 2(AB2 + BC2) = AC2 + BD2.
 Xem đáp án
Xem đáp án
a) Do ABCD là hình bình hành nên BC = AD; AB = DC.
Và AB//CD nên
Áp dụng định lí côsin cho hai tam giác ABD và ADC ta có:
BD2 = AD2 + AB2 – 2.AD.AB.cosA = BC2 + AB2 – 2.BC.AB.cosA
AC2 = AD2 + DC2 – 2.AD.DC.cosD = BC2 + AB2 + 2.BC.AB.cosA
Khi đó : BD2 + AC2 = 2AB2 + 2BC2 = 2(AB2 + BC2).
Vậy 2(AB2 + BC2) = AC2 + BD2.
Câu 45:
b) Cho AB = 4; BC = 5; BD = 7. Tính AC.
 Xem đáp án
Xem đáp án
b) Thay AB = 4, BC = 5, BD = 7 vào biểu thức 2(AB2 + BC2) = AC2 + BD2 ta được:
2.(42 + 52) = AC2 + 72 ⇒ AC2 = 2.(42 + 52) – 72 = 33
Vậy .
Câu 46:
Giải phương trình:
(12x + 7)2(3x + 2)(2x + 1) = 3
 Xem đáp án
Xem đáp án
(12x + 7)2(3x + 2)(2x + 1) = 3
⇔ (12x + 7)2.4.(3x + 2).6.(2x + 1) = 3.4.6
⇔ (12x + 7)2(12x + 8)(12x + 6) = 72
Đặt 12x + 7 = t ta có:
t2(t + 1)(t – 1) = 72
⇔ t2(t2 – 1) = 72
⇔ t4 – t2 – 72 = 0
⇔ t4 – 9t2 + 8t2 – 72 = 0
⇔ t2(t2 – 9) + 8(t2 – 9) = 0
⇔ (t2 – 9)(t2 + 8) = 0
⇔ t2 – 9 = 0 (Do t2 + 8 > 0)
⇔ t = ±3
Với t = 3 ta có:
12x + 7 = 3 ⇔
Với t = −3 ta có:
12x + 7 = −3
Vậy tập nghiệm của phương trình đã cho là .
Câu 47:
 Xem đáp án
Xem đáp án
(a + b)3 – (a – b)3 – 2b3
= a3 + 3a2b + 3ab2 + b3 – (a3 – 3a2b + 3ab2 – b3) – 2b3
= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3) – 2b3
= (a3 – a3) + (3a2b +3a2b) + (3ab2 – 3ab2) + (b3 + b3– 2b3)
= 0 + 6a2b + 0 + 0 = 6a2b
Câu 48:
Cho hàm số y = f(x) liên tục trên R. Biết rằng hàm số y = f '(x) có đồ thị như hình vẽ. Hàm số y = f(x2 – 5) nghịch biến trên khoảng nào sau đây?
 Xem đáp án
Xem đáp án
Xét hàm số y = f(x2 – 5).
Ta có y' = 2x.f '(x2 – 5)
y' = 0
Ta có bảng xét dầu:
|
x |
−2 −1 0 1 2 |
|
y’ |
− 0 + 0 − 0 + 0 − 0 + 0 − 0 + |
Từ bảng biến thiên ta có hàm số nghịch biến trên khoảng (0; 1).
Câu 49:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Biết BH = 4 cm, HC = 9 cm.
a) Tính độ dài DE.
 Xem đáp án
Xem đáp án
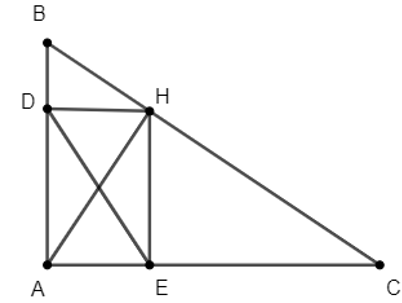
a) Xét tứ giác ADHE có: ; ; .
Suy ra ADHE là hình chữ nhật.
⇒ AH = DE
Xét tam giác ABC vuông tại A nên ta có:
AH2 = BH.CH = 4.9 = 36
⇒ AH = 6 (cm) = DE
Vậy DE = 6 cm.
Câu 50:
b) Chứng minh AD.AB = AE.AC.
 Xem đáp án
Xem đáp án
b) Xét ∆AHB vuông tại H có đường cao HD nên ta có:
AH2 = AD.AB (1)
Xét ∆AHC vuông tại H có đường cao HE nên ta có:
AH2 = AE.AC (2)
Từ (1) và (2) suy ra AD.AB = AE.AC (đpcm)
Câu 51:
Cho tam giác ABC vuông tại A và AB = AC. Trên cạnh AB, AC lấy hai điểm D và E sao cho AD = AE. Từ A và D kẻ đường thẳng vuông góc với BE cắt BC tại M và N. Tia ND cắt CA ở I. Chứng minh A là trung điểm của CI.
 Xem đáp án
Xem đáp án
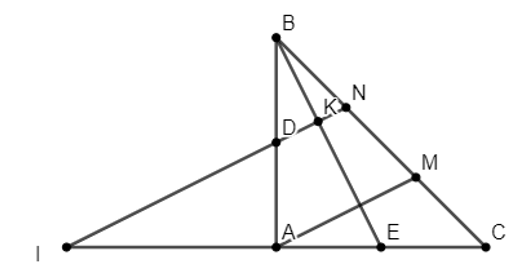
Gọi K là giao điểm của DN và BE
Ta có:
∆BKD vuông tại K có:
(1)
∆ABC vuông tại A có:
(2)
Từ (1) và (2) ta có:
(Vì và là 2 góc đối đỉnh)
Xét ∆DAI vuông tại A và ∆EAB vuông tại A có:
AD = AE (gt)
(cmt)
∆DAI = ∆EAB (g.cg)
⇒ AI = AB = AC
Hay A là trung điểm của CI (đpcm).
Câu 52:
 Xem đáp án
Xem đáp án
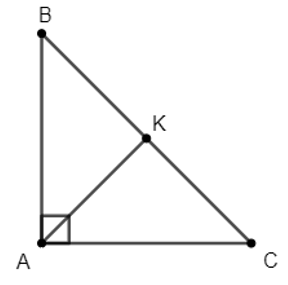
Xét ∆AKB và ∆AKC có:
AK cạnh chung
BK = KC (gt)
AB = AC (gt)
⇒ ∆AKB = ∆AKC (c.c.c)
⇒
Vì (hai góc kề bù) (1)
Mà (2)
Từ (1) và (2) suy ra
Vậy AK ⊥ BC (đpcm)
Câu 53:
Tính diện tích hình thang, biết các đáy có độ dài là 7 cm và 9 cm, một trong các cạnh bên dài 8 cm và tạo với một đáy một góc có số đo bằng 30°.
 Xem đáp án
Xem đáp án
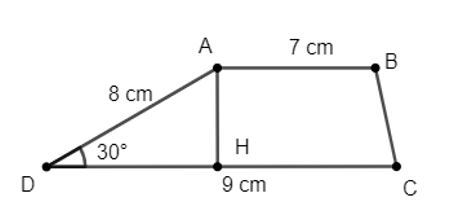
Gọi hình thang với các số liệu nêu trên là hình thang ABCD, trong dó AB là đáy nhỏ, BC là đáy lớn (AB//CD). Giả sử cạnh bên có độ dài 8 cm là cạnh AD, .
Kẻ AH CD (H ∈ CD)
Xét ∆AHD vuông tại H có:
(cm)
0 (cm2)
Câu 54:
Tìm GTNN và GTLN của hàm số: y = sinx + cosx.
 Xem đáp án
Xem đáp án
y = sinx + cosx
Ta có: −1 ≤ sinx ≤ 1
Vậy ; .
Câu 55:
Gọi (H) là hình tròn xoay thu được khi cho tam giác đều ABC có cạnh a quay quanh AB, tính thể tích khối tròn xoay giới hạn bởi (H).
 Xem đáp án
Xem đáp án
Khi cho ∆ABC đều có cạnh a quay quanh Ab ta thu được hai khối hình nón có cùng chiều cao và cúng bán kính đáy
Do đó .
Câu 56:
Một hình chữ nhật có độ dài cạnh lần lượt là 15 cm, 12 cm, nếu giảm một cạnh đi 3 cm thì phải tăng cạnh kia bao nhiêu cm để diện tích chữ nhật không đổi.
 Xem đáp án
Xem đáp án
Lời giải:
Diện tích ban đầu là: 15 × 12 = 180 (cm2)
Chiều dài sau giảm là: 15 – 3 = 12 (cm)
Cạnh còn lại phải có độ dài để diện tích không đổi là: 180 : 12 = 15 (cm)
Vậy chiều rộng tăng: 15 – 12 = 3 (cm)
Nếu giảm chiều rộng 3 cm thì chiều rộng còn: 12 – 3 = 9 (cm)
Cạnh còn lại phải có độ dài để diện tích không đổi là: 180 : 9 = 20 (cm)
Vậy chiều dài phải tăng: 20 – 15 = 5 (cm).
Câu 57:
Tìm m để phương trình sau có nghiệm: x2 – mx + m + 3 = 0.
 Xem đáp án
Xem đáp án
Phương trình đã chó có nghiệm khi ∆ ≥ 0
⇔ m2 – 4(m + 3) ≥ 0
⇔ m2 – 4m – 12 ≥ 0
Vậy với m ∈ (- ; −2] ∪ [6; + ) thì thỏa mãn yêu cầu bài toán.
Câu 58:
Tìm x, biết:
a) (8x2 – 4x) : (−4x) – (x + 2) = 8;
b) (2x4 – 3x3 + x2) : (−x2) + 4(x – 1)2 = 0.
 Xem đáp án
Xem đáp án
a) (8x2 – 4x) : (−4x) – (x + 2) = 8
−2x + 1 – x – 2 = 8
−3x = 9
x = −3.
Vậy x = −03.
b) (2x4 – 3x3 + x2) : (−x2) + 4(x – 1)2 = 0
−2x2 + 3x – 1 + 4x2 – 8x + 4 = 0
2x2 – 5x + 3 = 0
2x2 – 2x – (3x – 3) = 0
2x(x – 1) – 3(x – 1) = 0
(x – 1)(2x – 3) = 0
x – 1 = 0 hoặc 2x – 3 = 0
x = 1 hoặc
Vậy .
Câu 59:
Rút gọn biểu thức:
4x2(5x2 + 3) – 6x (3x2 – 2x + 1) – 5x3(2x – 1)
 Xem đáp án
Xem đáp án
4x2(5x2 + 3) – 6x (3x2 – 2x + 1) – 5x3(2x – 1)
= 4x2.5x2 + 4x2.3 + (–6x).3x2 + (–6x).( –2x) + (–6x).1 + (–5x3).2x + (–5x3).( –1)
= 20x4 + 12x2 + (–18x3) + 12x2 + (–6x) + (–10x4) + 5x3
= 20x4 + 12x2 – 18x3 + 12x2 – 6x – 10x4 + 5x3
= (20x4 – 10x4) + (–18x3 + 5x3) + (12x2 + 12x2) – 6x
= 10x4 + (–13x3) + 24x2 – 6x
= 10x4 – 13x3 + 24x2 – 6x.
Câu 60:
0.1 vs 0.125 cái nào lớn hơn
 Xem đáp án
Xem đáp án
Ta có: 0,1 = 0,100
Vì 0,100 < 0,125 nên 0,1 < 0,125.
