Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 29)
-
2095 lượt thi
-
53 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC có , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. Chứng minh rằng AD = AE.
 Xem đáp án
Xem đáp án
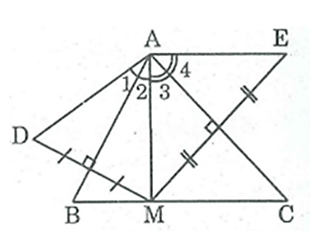
Vì D đối xứng với M qua trục AB
⇒ AB là đường trung trực của MD.
⇒ AD = AM (t/chất đường trung trực) (1)
Vì E đối xứng với M qua trục AC
⇒ AC là đường trung trực của ME
⇒ AM = AE (t/chất đường trung trực) (2)
Từ (1) và (2) suy ra: AD = AE.
Câu 2:
Một thửa ruộng hình chữ nhật chu vi bằng 0,3 km, có chiều dài gấp chiều rộng. Người ta mở rộng thửa ruộng đó theo chiều dài và theo chiều rộng, mỗi chiều 5m để được một hình chữ nhật mới. Hỏi diện tích của thửa ruộng mới là bao nhiêu mét vuông? Bao nhiêu hec- ta.
 Xem đáp án
Xem đáp án
Nửa chu vi thửa ruộng HCN là:
0,3 : 2 = 0,15 (km) = 150 (m)
Chiều dài thửa ruộng HCN lúc đầu là:
150 : (3 + 2) × 3 = 90 (m)
Chiều rộng thửa ruộng HCN lúc đầu là:
150 : (3 + 2) × 2 = 60 (m)
Chiều dài thửa ruộng HCN lúc sau là:
90 + 5 = 95 (m)
Chiều rộng thửa ruộng HCN lúc sau là:
60 + 5 = 65 (m)
Diện tích của thửa ruộng HCN mới là :
95 × 65 = 6175 (m2) = 0,6175 (ha)
Đáp số: 6175 m2; 0,6175 ha.
Câu 3:
 Xem đáp án
Xem đáp án
Câu 4:
Bạn Anh có 400 000 đồng tiền tiết kiệm. Bạn Anh tính sẽ dùng số tiền để ủng hộ các bạn học sinh nghèo, bạn giữ cho mình 70 000 đồng để ăn quà. Số tiền còn lại Anh dùng để mua một số tập, một cuốn tập có giá là 8000 đồng. Hỏi bạn Anh đã mua được bao nhêu quyển tập?
 Xem đáp án
Xem đáp án
Số tiền Anh dùng để ủng hộ các bạn học sinh nghèo là:
400000 × = 250000 (đồng)
Số tiền còn lại của Anh là:
400000 − 250000 − 70000 = 80000 (đồng)
An mua được số quyển tập là:
80000 : 8000 = 10 (quyển)
Đ/s: 10 quyển tập.
Câu 5:
Bạn Bình có 400 nghìn đồng tiết kiệm. Bạn tính sẽ dùng số tiền để ủng hộ các bạn học sinh nghèo, bạn giữ lại cho mình 90 nghìn đồng để ăn quà. Số tiền còn lại bạn dùng để mua tập, mỗi cuốn tập giá 8 nghìn đồng. Hỏi Bình mua được bao nhiêu cuốn tập?
 Xem đáp án
Xem đáp án
Số tiền bạn Bình dùng để ủng hộ các bạn học sinh nghèo là:
400000 × = 250000 (đồng)
Số tiền còn lại của bạn Bình là:
400000 − 250000 − 90000 = 60000 (đồng)
An mua được số cuốn tập là:
60000 : 8000 = 7 (cuốn) dư 5 000 (đồng)
Đáp số: 7 cuốn tập.
Câu 6:
Một mảnh vườn hình chữ nhật có chiều dài bằng chiều rộng. Các số đo chiều dài và chiều rộng theo đơn vị mét là số tự nhiên. Biết rằng diện tích của mảnh vườn đó nằm trong khoảng từ 90m2 đến 100m2. Vậy chu vi mảnh vườn đó là bao nhiêu mét?
 Xem đáp án
Xem đáp án
Diện tích chiếm số phần là :
3 × 2 = 6 (phần)
Từ 90 → 100, ta thấy chỉ có 96 là chia hết cho 6. Từ đó ta suy ra, diện tích mảnh vườn là : 964 m².
Ta chia diện tích mảnh vườn thành 6 hình vuông nhỏ:
96 : 6=16 (m²)
Mà 16 = 4 × 4 → Cạnh của hình vuông là 4 m.
Chiều dài của mảnh vườn là:
4 × 3 = 12 (m)
Chiều rộng của mảnh vườn là:
4 × 2 = 8 (m)
Chu vi của mảnh vườn là:
(12 + 8) × 2 = 40 (m)
Đáp số: 40 m.
Câu 7:
Tìm số tự nhiên a, b biết rằng
a, a − b = 5 và BCNN(a, b) = 60.
 Xem đáp án
Xem đáp án
a,
BCNN(a, b) = 60 ⇒ 60 ⋮ a, 60 ⋮ b. Hay a, b là ước tự nhiên của 60.
Các ước tự nhiên của 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Vì a − b = 5 nên a > b.
Ta xét bảng sau:
|
a |
6 |
10 |
15 |
20 |
|
b |
1 |
5 |
10 |
15 |
|
BCNN (a, b) |
6 |
5 |
30 |
60 |
|
|
Loại |
Loại |
Loại |
Nhận |
Vậy cặp số tự nhiên cần tìm là 20 và 15.
Câu 8:
Tìm số tự nhiên a, b biết rằng
b, ƯCLN(a, b) = 5 và BCNN(a, b) = 150.
 Xem đáp án
Xem đáp án
b,
ƯCLN (a, b) = 5 ⇒ a = 5a1; b = 5b1 và (a1, b1) = 1
Ta có a ∙ b = 5 ∙ 150 = 750 ⇒a1 ∙ b1= 30
Ta có bảng sau:
|
a1 |
1 |
2 |
3 |
5 |
|
a |
5 |
10 |
15 |
25 |
|
b1 |
30 |
15 |
10 |
6 |
|
b |
150 |
75 |
50 |
30 |
Vì vai trò của a, b như nhau nên ta có các cặ đảo ngược vị trí.
Vậy các cặp số tự nhiên (a, b) cần tìm là: (5, 150); (150, 5); (10, 75); (75, 10); (15, 50); (50, 15); (25, 30); (30, 25)
Câu 9:
Viết tập hợp các số tự nhiên lớn hơn 10 và nhỏ hơn 15 bằng 2 cách.
 Xem đáp án
Xem đáp án
Cách 1: A = {11; 12; 13; 14}
Cách 2: A = {x ∈ ℕ | 10 < x < 15}
Câu 10:
Viết số thập phân thích hợp vào chỗ chấm:
42dm 4cm = .... dm.
 Xem đáp án
Xem đáp án
42dm 4cm = 42,4 dm.
Câu 11:
 Xem đáp án
Xem đáp án
Ta có: n2 + n = n (n + 1)
Vì n (n + 1) là tích 2 số tự nhiên liên tiếp nên n (n + 1) ⋮ 2
⇒ n2 + n ⋮ 2.
Câu 12:
 Xem đáp án
Xem đáp án
n là số lẻ nên n = 2k + 1
Ta có : n2 = (2k + 1)2 = 4k2 + 4k + 1 = 4k (k + 1) + 1
Mà 4k (k + 1) ⋮ 4 nên n2 : 4 dư 1 (đpcm)
Câu 13:
Cho 3 đơn thức (a, b, c ≠ 0). Hỏi 3 đa thức trên cùng nhận giá trị âm được không? Vì sao?
 Xem đáp án
Xem đáp án
Nếu 3 đa thức cùng mang giá trị âm thì tích của chúng sẽ là 1 số âm.
Mà khi ta nhân 3 đa thức với nhau nhận kết quả là
Vì thế 3 đa thức không thể cùng nhận giá trị âm.
Câu 15:
Trong thúng có 210 quả quýt và cam. Mẹ đã bán 60 quả quýt, lúc này số quýt còn lại bằng số cam. Hỏi lúc đầu trong thúng có bao nhiêu quả cam, bao nhiêu quả quýt?
 Xem đáp án
Xem đáp án
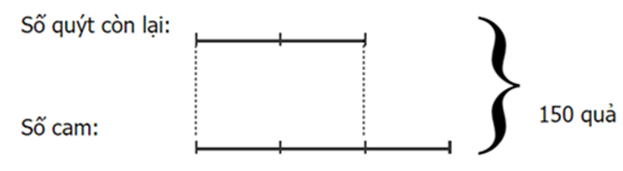
Theo sơ đồ, tổng số phần bằng nhau là:
2 + 3 = 5 (phần)
Số quả quýt còn lại là:
(150 : 5) × 2 = 60 (quả)
Số quả quýt lúc đầu trong thúng có là:
60 + 60 = 120 (quả)
Số quả cam lúc đầu trong thúng có là:
210 − 120 = 90 (quả)
Đáp số: 90 quả cam, 120 quả quýt.
Câu 16:
An và Bình mua chung 45 quyển vở và phải trả hết số tiền là 72000 đồng. Biết An phải trả nhiều hơn Bình 11200 đồng. Hỏi mỗi bạn đã mua bao nhiêu quyển vở.
 Xem đáp án
Xem đáp án
Giá tiền của mỗi quyển vở là:
72000 : 45 = 1600 (đồng)
An hơn Bình số quyển vở là:
11200 : 1600 = 7 (quyển)
An mua số quyển vở là:
(45 + 7) : 2 = 26 (quyển vở)
Bình mua số quyển vở là:
45 − 26 = 19 (quyển vở)
Đáp số: An mua 26 quyển vở.
Bình mua 19 quyển vở.
Câu 17:
Ba bạn Lan, Đào, Hồng có tất cả 27 cái kẹo. Nếu Lan cho Đào 5 cái, Đào cho Hồng 3 cái, Hồng cho lại Lan một cái thì số kẹo của ba bạn bằng nhau. Hỏi lúc đầu mỗi bạn có mấy cái kẹo?
 Xem đáp án
Xem đáp án
Sau khi cho số kẹo mỗi bạn là:
27 : 3 = 9 (cái)
Số kẹo của Lan ban đầu là:
9 + 5 − 1 = 13 (cái)
Số kẹo của Đào ban đầu là:
9 + 3 − 5 = 7 (cái)
Số kẹo của Hồng ban đầu là:
9 + 1 − 3 = 7 (cái)
Vậy lúc đầu bạn Lan có 13 cái, bạn Đào có 7 cái và bạn Hồng có 7 cái.
Câu 18:
Bạn Hải cho các viên bi vào hộp lần lượt theo thứ tự là: bi xanh, bi đỏ, bi vàng rồi lại đến bi xanh, bi đỏ, bi vàng ... cứ như vậy. Hỏi:
a) Viên bi thứ 100 có màu gì?
 Xem đáp án
Xem đáp án
a)
Ta thấy, cứ 3 viên bi thì lập thành 1 nhóm màu: xanh, đỏ, vàng. 100 viên bi thì có số nhóm là: 100 : 3 = 33 nhóm (dư 1 viên bi)
Như vậy, bạn Hải đã cho vào hộp được 33 nhóm, còn dư 1 viên của nhóm thứ 34 và là viên bi đầu tiên của nhóm này. Vậy viên bi thứ 100 có màu xanhCâu 19:
b) Muốn có 10 viên bi đỏ thì phải bỏ vào hộp ít nhất bao nhiêu viên bi?
 Xem đáp án
Xem đáp án
b)
Một nhóm thì có 3 viên bi, muốn có 10 viên bi đỏ thì cần bỏ vào hộp:
3 × 10 = 30 viên bi.
Nhưng viên bi màu đỏ là viên bi thứ 2 của nhóm.
Vậy cần bỏ vào hộp ít nhất số viên bi là: 30 − 1= 29 viên.
Câu 20:
Cho (2a + 7b) chia hết cho 3 (a, b thuộc ℕ). CMR: (4a + 2b) chia hết cho 3.
 Xem đáp án
Xem đáp án
Đặt A = 2a + 7b
B = 4a + 2b
Xét hiệu: 2A − B = 2 (2a + 7b) − (4a + 2b)
= 4a + 14b − 4a − 2b
= 12b
Vì A chia hết cho 3 nên 2A chia hết cho 3; 12b chia hết cho 3.
⇒ B chia hết cho 3 hay 4a + 2b chia hết cho 3 (đpcm)
Câu 21:
 Xem đáp án
Xem đáp án
x2 – x – a = 0 ⇒ x (x + 1) = a
Ta có số nguyên tố thì không chia hết cho số nào ngoài 1 và chính nó.
Vậy a là số nguyên tố thì .
TH1: x = 0
0 ∙ 1 = a
0 = a (KTM)
TH2: x = 1
1 ∙ (1 + 1) = a
2 = a (TM)
Vậy chỉ có nghiệm x duy nhất là x = 1.
Câu 22:
Cho tam giác ABC vuông tại A, đường cao AH biết AH = 12cm , HC = 16cm. Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
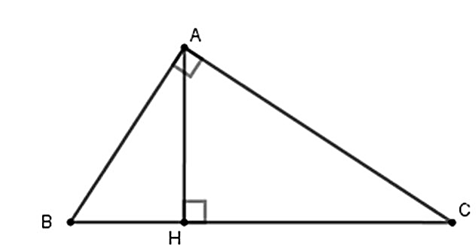
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức lượng ta có :
AH2 = HB ∙ HC
⇒
⇒ BC = HB + HC = 9 + 16 = 25 cm
Diện tích tam giác ABC là :
Câu 23:
Cho tam giác ABC vuông tại A, AH là đường cao (H thuộc BC), biết AH = 12cm, HC = 16cm. Tính HB và cosC.
 Xem đáp án
Xem đáp án
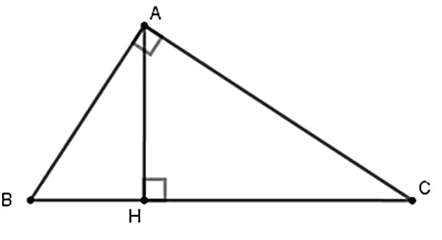
Áp dụng HTL:
AH2 = BH ⋅ HC
Áp dụng PTG:
Câu 24:
Cho tam giác ABC góc A = 90°. Gọi E, G, F là trung điểm của AB, BC, AC. Từ E kẻ đường song song với BF, đường thẳng này cắt GF tại I.
a) Tứ giác AEGF là hình gì?
 Xem đáp án
Xem đáp án
a:
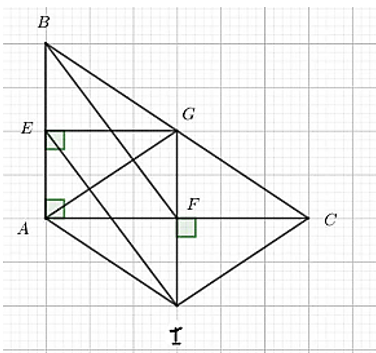
Xét ΔABC có:
G là trung điểm của BC
F là trung điểm của AC
Do đó: FG là đường trung bình.
⇒ FG // AE và FG = AE
⇒ AEGF là hình bình hành.
Mà
Nên AEGF là hình chữ nhật.
Câu 25:
b) Chứng minh tứ giác BEIF là hình bình hành.
 Xem đáp án
Xem đáp án
b:
Xét tứ giác BEIF có:
IF // BE
EI // BF
Do đó: BEIF là hình bình hành.
Câu 26:
c) Chứng minh tứ giác AGCI là hình thoi.
 Xem đáp án
Xem đáp án
c:
Ta có: EIFB là hình bình hành
Nên FI // EB và FI = EB
⇒ FI = IG
⇒ F là trung điểm của IG
Xét tứ giác CIAG có:
F là trung điểm của AC
F là trung điểm của GI
Do đó: CIAG là hình bình hành
Mà GA = GC
Nên CIAG là hình thoi (đpcm).
Câu 27:
Có 33 con chim đậu trên một sân hình vuông cạnh 4m. Chứng minh rằng có ít nhất 3 con chim đậu bên trong hoặc trên cạnh của 1 hình vuông cạnh 1m.
 Xem đáp án
Xem đáp án
Chia hình vuông cạnh 4m thành 16 hình vuông nhỏ cạnh 1 m.
Có 33 con chim trong 16 hình vuông.
Theo nguyên lí Diriclet tồn tại 1 hình vuông chứa ít nhất
+ 1 = 3 con chim (đpcm).
Câu 28:
Mai dùng 25000 đồng mua bút. Có hai loại bút: Loại 1 giá 2000 đồng một chiếc; loại 2 giá 1500 đồng một chiếc. Mai sẽ mua được nhiều nhất bao nhiêu bút nếu:
a. Mai chỉ mua bút loại 1.
b. Mai chỉ mua bút loại 2.
c. Mua cả hai loại bút với số lượng như nhau.
 Xem đáp án
Xem đáp án
a,
Mai chỉ mua bút loại 1 thì Mai mua được
25 000 : 2 000 = 12 cái bút (dư 1 000 đồng)
b,
Mai chỉ mua bút loại 2 thì Mai mua được
25 000 : 1 500 = 16 cái bút (dư 1 000 đồng)
c,
Mai mua cả hai loại bút với số lượng như nhau thì Mai mua được
25 000 : (2 000 + 1 500) = 7 cái (dư 500 đồng)
Câu 29:
Bạn Mai dùng 25000 đồng mua bút. Có hai loại bút : loại I giá 2000 đồng một chiếc, loại II giá 1500 đồng một chiếc. Bạn Mai mua được nhiều nhất bao nhiêu chiếc bút nếu: Mai chỉ mua bút loại II.
 Xem đáp án
Xem đáp án
Ta có:
25000 : 1500 = 16 (dư 1000)
Vậy Mai mua được nhiều nhất 16 bút loại II.
Câu 30:
Một bếp ăn chuẩn bị đủ thực phẩm cho 300 người ăn trong 4 ngày. Vì có thêm một số người đến ăn nên số thực phẩm đó chỉ đủ ăn trong 3 ngày. Hỏi số người mới đến là bao nhiêu? (Mức ăn như nhau).
 Xem đáp án
Xem đáp án
Nếu chỉ có 1 người ăn thì sẽ dùng hết số thực phẩm đó trong số ngày là:
300 × 4 = 1200 (ngày)
Số người ăn trong 3 ngày là:
1200 : 3 = 400 ( người)
Số người đến thêm là:
400 – 300 = 100 ( người)
Đáp số: 100 người.
Câu 31:
Tính chu vi một mảnh đất hình chữ nhật, biết chiều dài bằng chiều rộng và hơn chiều rộng 10m.
 Xem đáp án
Xem đáp án
Ta có sơ đồ:
Chiều dài: |-----||-----||-----|
Chiều rộng: |-----||-----|
Hiệu số phần bằng nhau:
3 – 2 = 1 (phần)
Chiều rộng hình chữ nhật:
10 : 1 × 2 = 20 (m)
Chu vi hình chữ nhật là:
(20 + 30) × 2 = 100 (m)
Đáp số: 100m.
Câu 32:
Một số chia 4 dư 3, chia 17 dư 9, chia 19 dư 13. Hỏi số đó chia cho 1292 thì dư bao nhiêu?
 Xem đáp án
Xem đáp án
Ta gọi a là số cần tìm.
Ta có:
a = 4b + 3 = 17c + 9 = 19d + 3 (b, c, d ∈ ℕ)
Mà a + 25 = 4b + 28 = 17c + 34 = 19d + 38
Ta thấy a + 25 chia hết cho 4, 17, 19
⇒ a + 25 chia hết cho 4 ∙ 17 ∙ 19 = 1292
⇒ a chia 1292 dư 1292 – 25 = 1267.
vậy số đó chia cho 1292 dư 1267.
Câu 33:
Một thửa ruộng hình chữ nhật có chu vi 360m, chiều rộng bằng chiều dài.
a) Tính diện tích thửa ruộng đó theo đơn vị đo ha.
 Xem đáp án
Xem đáp án
Nửa chu vi hình chữ nhật là
360 : 2 = 180 (m)
Ta có sơ đồ:
chiều dài:7 phần
chiều rộng: 2 phần
Tổng số phần bằng nhau là:
2 + 7 = 9 (phần)
Chiều dài hình chữ nhật là:
(180 : 9) × 7 = 140 (m)
Chiều rộng hình chữ nhật là:
(180 : 9) × 2 = 40 (m)
a)
Diện tích hình chữ nhật là:
140 × 40 = 5600(m2) = 0,56 ha.
Câu 34:
b) Biết trung bình cứ 100m2 của thửa ruộng thu được 75kg thóc. Hỏi trên cả thửa ruộng thu hoạch được bao nhiêu tấn thóc.
 Xem đáp án
Xem đáp án
b)
Trên cả thửa ruộng đó thu hoạch được số tấn thóc là:
(5600 : 100) × 75 = 4200(kg) = 4,2 tấn.
Đáp số a) 0,56 ha.
b) 4,2 tấn.
Câu 35:
Một thửa ruộng hình chữ nhật có chu vi là 360 m. Chiều rộng bằng chiều dài. Tính diện tích thửa ruộng đó.
 Xem đáp án
Xem đáp án
Nữa chu vi thửa ruộng hình chữ nhật là:
360 : 2 = 180 (m)
Chiều dài thửa ruộng hình chữ nhật là:
180 : (1 + 2) × 2 = 120 (m)
Chiều rộng thửa ruộng hình chữ nhật là:
180 − 120 = 60 (m)
Diện tích thửa ruộng hình chữ nhật là:
60 × 120 = 7200 (m2)
Đáp số : 7200 m2
Câu 36:
 Xem đáp án
Xem đáp án
Một người ăn trong số ngày là:
300 × 16 = 4800 (ngày)
Số người ăn hết số gạo đó trong 12 ngày là:
4800 : 12 = 400 (ngày)
Vậy có số người đến thêm là:
400 – 300 = 100 (người)
Đáp số: 100 người.
Câu 37:
Một đơn vị có 45 người đã chuẩn bị đủ gạo ăn trong 15 ngày. Sau khi ăn được 5 ngày đơn vị đó tiếp nhận thêm 5 người nữa. Hãy tính xem số gạo còn lại đủ cho đơn vị ăn trong bao nhiêu ngày?
 Xem đáp án
Xem đáp án
Số ngày còn lại đủ dùng số gạo theo dự định là:
15 − 5 = 10 (ngày)
Số người sau khi được bổ sung là:
45 + 5 = 50 (người)
Với 50 người thì số gạo còn lại đơn vị đó chỉ đủ ăn trong:
10 × 45 : 50 = 9 (ngày)
Đáp số: 9 ngày.
Câu 42:
Viết số bé nhất có 5 chữ số và có tổng các chữ số bằng 40.
 Xem đáp án
Xem đáp án
Ta có: 9 × 4 = 36, 9 × 5 = 45 mà 36 < 40 < 45, do đó số có 5 chữ số cần lập phải có 4 chữ số 9. Từ đó suy ra chữ số thứ 5 của số đó là 40 – 36 = 4.
Để nó là số bé nhất, ta chọn số 49 999.
Vậy số bé nhất có 5 chữ số và có tổng các chữ số bằng 40 là 49 999.
Câu 43:
Khối 6 của trường chưa tới 400 học sinh khi xếp hàng 10,12,15 đều dư 3 nhưng nếu xếp hàng 11 thì không dư . Tính số học sinh khối 6.
 Xem đáp án
Xem đáp án
Gọi số học sinh của khối 6 là a. (0 < a < 400)
Ta có :
a : 10; a : 12; a : 15 đều dư 3
⇒ a − 3 chia hết cho10; 12; 15
⇒ a − 3 thuộc BC(10; 12; 15)
BCNN(10; 12; 15) = 60
⇒ a − 3 thuộc {0; 60; 120; 180; 240; 360; 420; ...}
⇒ a thuộc {3; 63; 123; 183; 243; 363; 423; ....}
Mà a < 400 và a chia hết cho 11.
Vậy a = 363.
Câu 44:
 Xem đáp án
Xem đáp án
Gọi số nhỏ nhất cần tìm là a (a ∈ ℕ*)
Vì a chia 3 dư 1; chia 4 dư 3; chia 5 dư 1 nên
a − 1 chia hết cho 3
a − 3 chia hết cho 4 ⇒ a − 3 + 4 = a − 1 chia hết cho 4
a − 1 chia hết cho 5
⇒ a − 1 ∈ BC (3; 4; 5) = {0; 60; 120; 180; ...}
Vì a là số tự nhiên nhỏ nhất nên a = 60.
Vậy số tự nhiên nhỏ nhất cần tìm là 60.
Câu 45:
Tìm số x thuộc ℤ biết x + 1 + x + 3 + x + 5 + ... + x + 99 = 0.
 Xem đáp án
Xem đáp án
(x + 1) + (x + 3) + (x + 5) + ... +(x + 99) = 0
Tổng các số hạng là: (99 + 1) : 2 = 50 (số hạng)
⇒ (x + 1) + (x + 3) + ... + (x + 99) = 0
⇔ 50x + (1 + 3 + 5 + ... + 99) = 0
⇔ 50x + (99 + 1) ∙ 5022(99 + 1) ∙ 50=0
⇔ 50x + 2500 = 0
⇒ x = = – 50.
Vậy x = – 50 thỏa mãn đề bài.
Câu 46:
 Xem đáp án
Xem đáp án
Hiệu số 2 số đó là:
5 × 2 = 10
Số lẻ bé là:
(70 − 10 ) : 2 = 30.
Số lẻ lớn là:
70 − 30 = 40.
Đáp số: 40 và 30.
Câu 48:
Ở một lớp học, nếu xếp mỗi bàn 4 bạn thì có 1 bạn chưa có chỗ ngồi, nếu xếp mỗi bàn 5 bạn thì thừa 2 bàn. Hỏi lớp có bao nhiêu học sinh và bao nhiêu bàn?
 Xem đáp án
Xem đáp án
1 bàn xếp 4 bạn thì 1 bạn chưa có chỗ ngồi.
1 bàn xếp 5 bạn thì thừa 2 bạn, tức à thiếu: 5 × 2 = 10 (bạn) thì ngồi đủ số bàn.
Ta có sơ đồ:
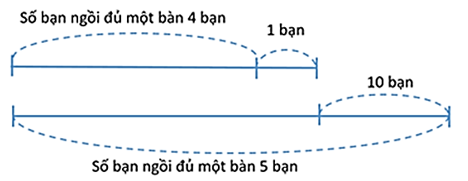
Nếu tất cả các bạn đều có 5 bạn ngồi thì số bạn sẽ nhiều hơn khi tất cả các bàn đều ngồi 4 bạn là: 1 + 10 = 11 (bạn)
1 bàn ngồi 5 bạn nhiều hơn 1 bàn ngồi 4 bạn là: 5 – 4 = 1 (bạn)
Số bàn là: 11 : 1 = 11 (bàn)
Số học sinh là: 4 × 11 + 1 = 45 (bạn)
Vậy lớp có 45 học sinh và 11 bàn học.
Câu 49:
viết dưới dạng phân số thập phân là bao nhiêu?
 Xem đáp án
Xem đáp án
Vậy viết dưới dạng phân số thập phân là: .
Câu 50:
Trung bình cộng số tuổi của bố, tuổi An và tuổi Hồng là 19. Tuổi bố hơn số tuổi của An và hồng là 2 tuổi. Hồng kém An 8 tuổi. Tính số tuổi của mỗi người.
 Xem đáp án
Xem đáp án
Trung bình tuổi 3 người là 19
⇒ Tổng tuổi 3 người là:
19 × 3 = 57
Gọi tổng tuổi của An và Hồng là số thứ nhất, tuổi bố là số thứ hai.
⇒ 2 lần số thứ nhất bằng: 57 – 25
Số thứ nhất là: (57 – 25) : 2 = 16 (tuổi)
Số thứ hai là: 16 + 25 = 41 (tuổi)
Số tuổi của Hồng là: (16 – 8) : 2 = 4 (tuổi)
Số tuổi của An là: 4 + 8 = 12 (tuổi)
Vậy: Bố 41 tuổi, An 12 tuổi và Hồng 4 tuổi.
Câu 51:
Tìm hai số biết hiệu là 603, biết rằng khi thêm một chữ số 0 vào bên phải số bé thì được số lớn.
 Xem đáp án
Xem đáp án
Thêm 1 chữ số 0 vào bên phải số bé thì số bé sẽ gấp lên: 10 lần
Ta có sơ đồ:
Số lớn: I-----I-----I-----I-----I-----I-----I-----I-----I-----I-----I
Số bé: I-----I
Hiệu số phần bằng nhau là:
10 − 1 = 9 (phần)
Số lớn là:
603 : 9 × 10 = 670
Số bé là:
670 − 603 = 67
Vậy số lớn là 670 và số bé là 67 thỏa mãn đề bài.
Câu 52:
Tổng hai số là 724. Tìm số lớn biết rằng khi xóa chữ số 7 ở hàng trăm của số lớn thì ta được số bé.
 Xem đáp án
Xem đáp án
Coi số bé là: ab; số lớn là 7ab.
Ta có:
ab + 700 + ab = 724
ab × 2 = 724 – 700 = 24
ab = 12
Số lớn là 712.
Câu 53:
Bác Vinh mua 1425 viên gạch bông để lát nền nhà. Bác dự tính sẽ thừa ra 125 viên đủ để lát 5m2 khu vệ sinh. Hỏi diện tích nền nhà cần lát gạch bông của bác Vinh là bao nhiêu mét vuông?
 Xem đáp án
Xem đáp án
Số viên gạch bông đủ để lát 1 m2 nền nhà là:
125 : 5 = 25 (viên)
Nền nhà của bác Vinh lát hết số viên gạch bông là:
1425 – 125 = 1300 (viên)
Diện tích nền nhà của bác Vinh là:
1300 : 25 = 52 (m2)
Đáp số: 52 m2.
