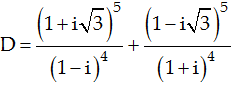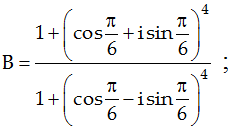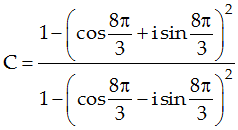100 câu trắc nghiệm Số phức nâng cao-P4 (có đáp án)
-
2974 lượt thi
-
26 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Biết z1; z2 là các số phức thỏa mãn điều kiện ![]() . Tìm |z1 + z2|
. Tìm |z1 + z2|
 Xem đáp án
Xem đáp án
Chọn D.
Gọi z = x + yi thì
Phương trình đã cho trở thành:
x2 - y2 + 2xyi + 2( x - yi) = 0
Suy ra: x2 - y2 + 2x + ( 2xy - 2y)i = 0
Với y = 0 thay vào phương trình (*) ta được: x2 + 2x = 0
Với x = 1 thay vào phương trình (*) ta được: y2 = 3
Vậy Suy ra: |z1 + z2| = 2.
Câu 2:
Biết z1; z2 là số phức thỏa điều kiện z2 - |z|2 + 1 = 0. Tính 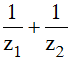
 Xem đáp án
Xem đáp án
Chọn D.
Đặt z = x + yi. Phương trình z2 - |z|2 + 1 = 0 trở thành:
x2 - y2 + 2xyi - ( x2 + y2) + 1 = 0
Suy ra: -2y2 + 1+ 2xyi = 0
Vậy số phức z cần tìm là: .Suy ra
Câu 3:
Biết z1; z2; z3; z4 là các số phức thỏa điều kiện .
Tính | z1| + | z2| + | z3| + | z4|
 Xem đáp án
Xem đáp án
Chọn A.
Đặt z = x + yi . Phương trình trở thành
( x - yi)2 = i(x + yi) hay x2 - y2 - 2xyi = -y + xi
Vậy số phức z cần tìm là: z = 0 ; z = i;
Suy ra | z1| + | z2| + | z3| + | z4| = 3.
Câu 5:
Gọi z là số phức khác 0 sao cho 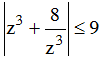 .Tìm khẳng định đúng
.Tìm khẳng định đúng
 Xem đáp án
Xem đáp án
Chọn A.
Ta có:
, mặt khác ta có:
|z1 + z2| ≤ |z1| + |z2|.
Do đó:
Đặt lúc đó ta được: a3 - 6a – 9 ≤ 0 hay ( a - 3) ( a2 + 3a + 3) ≤ 0
Suy ra: a ≤ 3.
Câu 6:
Cho phương trình z2 + mz - 6i = 0. Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng m = ± ( a + bi). Giá trị a + 2b là:
 Xem đáp án
Xem đáp án
Chọn D.
Gọi z1; z2 là hai nghiệm của phương trình đã cho
Theo Viet, ta có:
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
Suy ra: m2 = 5 - 12i
Do đó: m = ± ( 3 - 2i)
Vậy a = 3 ; b = -2 và a + 2b = -1
Câu 7:
Cho số phức z thỏa mãn điều kiện 11z10 + 10iz9 + 10iz -11 = 0. Tìm khẳng định đúng
 Xem đáp án
Xem đáp án
Chọn B.
Ta có : 11z10 + 10iz9 + 10iz - 11 = 0.
Hay z9( 11z + 10i) = 11 - 10iz
Hay:
Đặt z = x + yi. Từ (*) suy ra:
Xét các trường hợp:
+ Nếu |z| > 1 thì x2 + y2> 1 nên: g( x; y) =112( x2 + y2) + 102 + 220y = 102( x2 + y2) + 21( x2 + y2) + 102 + 220y > 102( x2 + y2) + 112 + 220y = f( x; y)
Do đó |z9 | < 1 ⇒ z < 1 (mâu thuẫn).
+ Nếu |z| < 1 thì x2 + y2 < 1 nên:
G( x; y) = 112( x2 + y2) + 102+220y = 102( x2+ y2) + 21( x2 + y2) + 102+ 220y < 102( x2 + y2) + 112+ 220y = f( x; y)
Suy ra |z9| > 1 ⇒ |z| > 1 (mâu thuẫn).
+ Nếu |z| = 1 thì g( x; y) = f( x; y) (thỏa mãn)
Vậy |z| = 1.
Câu 8:
Trong tập số phức, giá trị của m để phương trình bậc hai z2 + mz + i = 0 có tổng bình phương hai nghiệm bằng -4i là:
 Xem đáp án
Xem đáp án
Chọn A.
Gọi z1; z2 là hai nghiệm của phương trình.
Theo Viet, ta có:
Ta có: m2 - 2i = - 4i khi và chỉ khi m2 = -2i hay m = ±( 1 - i)
Câu 9:
Gọi z1 ; z2 là hai nghiệm của phương trình z2 + 2z+ 8= 0, trong đó z1 có phần ảo dương. Giá trị của số phức ![]() là:
là:
 Xem đáp án
Xem đáp án
Chọn C.
=
Câu 10:
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: 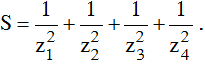
 Xem đáp án
Xem đáp án
Chọn C.
Không mất tính tổng quát ta gọi 4 nghiệm của phương trình là:
z1= 1; z2= - 2; z3= 1+ i và z4 = 1 - i
Thay vào biểu thức
Câu 11:
Cho z1; z2; z3; z4 là các nghiệm của phương trình: (z2 +1) (z2 - 2z + 2) = 0 . Tính ![]()
 Xem đáp án
Xem đáp án
Chọn C.
PT
S= i2014+ ( -i) 2014+ ( 1-i) 2014+ (1+ i) 2014
= ( i2) 1007+ [(-i)2]1007+ (-2i) 1007+ (2i) 1007= -1-1+( -2) 1007. i1007+ 21007. i1007= - 2
Câu 16:
Tìm số nguyên dương n bé nhất để 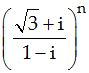 là số thực.
là số thực.
 Xem đáp án
Xem đáp án
Chọn B.
Ta có: ;
Do đó
Số đó là số thực khi và chỉ khi
Mà k nguyên nên số nguyên dương bé nhất cần tìm là n = 12.
Câu 22:
Cho z1; z2 là hai nghiệm phức của phương trình z2 - 2z + 4 = 0. Phần thực, phần ảo của số phức: 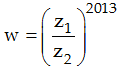 lần lượt là bao nhiêu, biết z1 có phần ảo dương.
lần lượt là bao nhiêu, biết z1 có phần ảo dương.
 Xem đáp án
Xem đáp án
Chọn C.
Vì Δ = -3 nên phương trình có hai nghiệm phức: (do z1 có phần ảo dương)
Ta có:
Do đó:
Vậy phần thực bằng 1, phần ảo bằng 0.
Câu 23:
Cho số phức z biết z= 1 + . Tìm tổng của phần thực và phần ảo của số phức w = (1 + i)z5
 Xem đáp án
Xem đáp án
Chọn D.
Ta có phương trình đã cho tương đương với phương trình:
Do đó:
Suy ra:
Vậy số phức w = (1 + i )z5 có phần thực là và phần ảo là
Tổng của phần thực và phần ảo là 32.
Câu 24:
Gọi z1; z2 là hai nghiệm phức của phương trình z2 – z + 1 = 0 . Phần thực, phần ảo của số phức ![]() lần lượt là?
lần lượt là?
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
Áp dụng công thức Moa-vrơ:
Phần thực của w là -1, phần ảo là 0.
Câu 25:
Cho các số phức z thỏa mãn: (2 - z)5 = z5. Hỏi phần thực của z là bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn B.
Ta có z = 0; z = 2 không thỏa mãn phương trình nên
nên đặt
Nên
Vậy z luôn có phần thực là 1.
Câu 26:
Cho phương trình 8z2 - 4(a + 1)z + 4a + 1 = 0 (1) với a là tham số. Tính tổng tất cả các giá trị của a để (1) có hai nghiệm z1; z2 thỏa mãn z1/ z2 là số ảo, trong đó z2 là số phức có phần ảo dương.
 Xem đáp án
Xem đáp án
Chọn B.
Từ giả thiết suy ra z1; z2 không phải là số thực.
Do đó Δ’ < 0, hay 4( a + 1)2 - 8(4a + 1) < 0
Hay a2 - 6a -1 < 0 (*)
Suy ra ,
Ta có z1/ z2 là số ảo khi và chỉ khi là số ảo
Tương đương: (a + 1)2 - (-(a2 - 6a - 1)) = 0 hay a2 - 2a = 0
Vậy a = 0 hoặc a = 2.
Đối chiếu với điều kiện (*) ta có giá trị của a là a = 0 hoặc a = 2.
Vậy tổng các giá trị của a là: 0 + 2 = 2

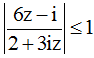 . Tìm khẳng định đúng
. Tìm khẳng định đúng