25 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Số phức nâng cao-P2 (có đáp án)

Câu 1:

Cho các số phức z thỏa mãn |z – 2 – 4i| = 2. Gọi z_1;z₂ số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?

A. 8i

B. 4

C. -8

D. 8

Xem đáp án

Chọn D.

Ta có

+ Giá trị lớn nhất của |z| là đạt được tại

+ Giá trị nhỏ nhất của |z| là , đạt được tại

Vậy tổng phần ảo là:

Câu 2:

Gọi z₁, z₂ lần lượt là hai nghiệm của phương trình z²- (1 + 3i) z – 2 + 2i = 0 và thỏa mãn | z₁| > | z₂|. Tìm giá trị của biểu thức

A. 0,5

B. 1,5

C. 1

D. 2

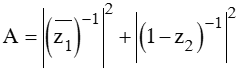
Xem đáp án

Chọn B.

Phương trình đã cho tương đương với:

( z – 2i) ( z – 1 – i) = 0

Suy ra: z = 2i hoặc z = 1 + i

Do | z₁| > | z₂| nên ta có z₁= 2i và z₂= 1 + i

Ta có

$= {|\frac{1}{- 2 i}|}^{2} + {|\frac{1}{- i}|}^{2} = {|\frac{i}{2}|}^{2} + {|i|}^{2} = \frac{1}{2} + 1 = \frac{3}{2}$ = 1,5

Câu 3:

Gọi z₁; z₂ lần lượt là hai nghiệm của phương trình z² – 4z + 7 = 0 .Tính giá trị của biểu thức

A. 1

B. 3

C. 0

D. 5

Xem đáp án

Chọn C.

Phương trình đã cho tương đương với:

( z - 2) ²= -3 hay

Từ đó

Do Q là biểu thức đối xứng với z₁; z₂ nên không mất tính tổng quát, giả sử

Lúc đó:

Câu 4:

Cho các số phức z thỏa mãn |z² + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?

Xem đáp án

Chọn A.

Ta có

Giải bất phương trình trên với ẩn |z| ta được:

Vậy

Câu 5:

Cho số phức z₁; z₂ thỏa mãn 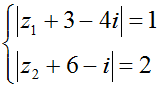. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức | z₁ - z₂ | là?

A. 18

B. $6 \sqrt{2}$

C. 6

D. $3 \sqrt{2}$

Xem đáp án

Chọn B.

Ta có

Do đó và

Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất là

Câu 6:

Trong các số phức z thỏa mãn điều kiện |z – 1 – 2i| = 2, tìm số phức z có môđun nhỏ nhất.

Xem đáp án

Chọn C.

Gọi z = x + yi và M (x; y) là điểm biểu diễn số phức z.

Ta có : |z – 1 – 2i| = 2 hay ( x - 1) ²+ (y - 2)²= 4

Đường tròn (C): ( x - 1)²+ (y - 2)²= 4 có tâm I(1; 2). Đường thẳng OI có phương trình y = 2x

Số phức z thỏa mãn điều kiện và có môdun nhỏ nhất khi và chỉ khi điểm biểu diễn số phức đó thuộc đường tròn (C) và gần gốc tọa độ O nhất, điểm đó chỉ là một trong hai giao điểm của đường thẳng OI với (C), khi đó tọa độ của nó thỏa mãn hệ

hoặc

Chọn nên số phức

Câu 7:

Cho số phức z thỏa mãn . Giá trị nhỏ nhất và giá trị lớn nhất của modul z lần lượt là.

Xem đáp án

Chọn B.

Giả sử z = x + yi. Từ giả thiết:

Suy ra: ( x + 2) ²+ ( y - 1)²= 2[(x + 1) ²+ ( y + 1) ²]

Hay x²+ (y + 3)²= 10

Tập hợp điểm biểu diễn của z là đường tròn tâm I(0; -3) bán kính

Gọi M là điểm biểu diễn của z, ta có:

IM-IO ≤ OM ≤ IM+ IO hay

Câu 8:

Cho số phức z thỏa mãn là một số thực. Hỏi giá trị nhỏ nhất của |z| gần với giá trị nào nhất?

A. 2,7

B. 2,8

C. 1,3

D. 1,4

Xem đáp án

Chọn B.

Giả sử z = x + yi.

Từ giả thiết: = ( x + 3 + ( y - 1) i) ( x + 1 - ( y - 3) i)

= x²+ y²+ 4x - 4y + 6 + 2( x – y + 4) i

Để số trên là 1 số thực khi và chỉ khi : x – y + 4 = 0

Tập hợp biểu diễn của z là đường thẳng d: x – y + 4 = 0.

Gọi M là điểm biểu diễn của z.

Tìm được M ( -2; 2) nên z = -2+ 2i . Suy ra:

Lại có: $2 \sqrt{2} \approx 2, 8$

Câu 9:

Trong các số phức z thỏa mãn |z + 4 - 3i| + |z -8 - 5i| = 2 $\sqrt{38}$ . Tìm giá trị nhỏ nhất của |z – 2 – 4i| ?

A. 1/2

B. 5/2

C. 2

D. 1

Xem đáp án

Chọn D.

Gọi M( x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.

Khi đó

Áp dụng bất đẳng thức Bunhiakovsky ta có:

Vậy Min|z – 2 – 4i| = 1

Câu 10:

Cho hai số phức z₁ và z₂ thỏa mãn | z₁ + 2 z₂| = 5 và |3 z₁ - z₂| = 3. Giá trị lớn nhất của P = | z₁| + | z₂| gần với số nguyên nào nhất?

A. 2

B. 3

C.4

D. 5

Xem đáp án

Chọn B.

Ta có

Từ (1) và (2) suy ra

Áp dụng bất đẳng thức Bunyakovsky ta có:

. Vậy

Lại có: $\sqrt{\frac{155}{14}} \approx 3$

Câu 11:

Cho số phức $z = {(\frac{2 + 6 i}{3 - i})}^{m}$ với m nguyên. Có bao nhiêu giá trị của m với 1≤ m≤ 50 để z là số thuần ảo?

A. 26.

B. 25.

C. 24.

D. 50.

Xem đáp án

Chọn B.

+ Ta có

Do đó:

+ để z là số thuần ảo khi và chỉ khi m = 2k + 1

+ Mà 0 ≤ m ≤ 50 nên 0 ≤ 2k + 1 ≤ 50

Suy ra: -1/2 ≤ k ≤ 24,5

Kết hợp với điều kiện k nguyên nên k ∈ {0;1;2;3...24}

Với 25 giá trị của k cho ta tương ứng 25 giá trị m thỏa yêu cầu đề bài.

Câu 12:

Cho biểu thức L = 1- z+ z²- z³+ ...+ z²⁰¹⁶- z²⁰¹⁷ với 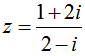. Biểu thức L có giá trị là

A. 1 - i.

B. 1 + i.

Xem đáp án

Chọn A.

+ Ta có:

+ Khi đó: L = 1- z+ z²- z³+ ...+ z²⁰¹⁶- z²⁰¹⁷

Câu 13:

Cho 2 số phức 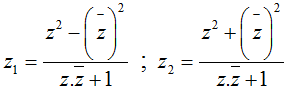; với z = x+ yi.

Mệnh đề nào sau đây đúng?

A. z₁ và z₂ là số thuần ảo.

B. z₂là số thuần ảo.

C. z₁là số thuần ảo.

D. z₁và z₂là số thực.

Xem đáp án

Chọn C.

Ta có: z = x+ yi nên z²= x²- y²+ 2xyi

Khi đó :

Suy ra z₁ là số thuần ảo; z₂là số thuần thực.

Câu 14:

Cho $z_{1} = 1 + \sqrt{3} i$ ; $z_{2} = \frac{7 + i}{4 - 3 i}; z_{3} = 1 - i$ . Tính $w = z_{1}^{25} . z_{2}^{10} . z_{3}^{2016}$

Xem đáp án

Chọn B.

Câu 15:

Cho số phức $z = \frac{- m + i}{1 - m (m - 2 i)}, m \in ℝ$ . Tìm |z|_max

A.1/2.

B. 0.

C. 1.

D. 2.

Xem đáp án

Chọn C.

Ta có:

Câu 16:

Cho số phức z thỏa mãn |z +1 +i | =| $\bar{z}$ - 2i |. Tìm giá trị nhỏ nhất của |z|.

A. $\sqrt{2}$

B. 1

C. $\frac{1}{\sqrt{2}}$

D. 2

Xem đáp án

Chọn C.

Gọi z = x+ yi thì M (x; y) là điểm biểu diễn z

Ta có |z +1 +i | =| $\bar{z}$ - 2i |

Nên ( x + 1) ²+ (y + 1) ²= x²+ (y + 2) ² hay ∆: x – y – 1 = 0.

Do đó điểm M di chuyển trên ∆. Do đó; để modul của số phức z min khi M là hình chiếu của O trên ∆

Vậy

Câu 17:

Tính tổng $L = C_{2016}^{0} - C_{2016}^{2} + C_{2016}^{4} - C_{2016}^{6} + . . . . . - C_{2016}^{2014} + C_{2016}^{2016}$

A. 2¹⁰⁰⁸

B. -2¹⁰⁰⁸

C.¹⁰⁰⁶

D. -2¹⁰⁰⁶

Xem đáp án

Chọn A.

+ Ta có:

${(1 - i)}^{2016} = C_{2016}^{0} - C_{2016}^{1} i + C_{2016}^{2} i^{2} - C_{2016}^{3} i^{3} + . . . - C_{2016}^{2015} i^{2015} + C_{2016}^{2016} i^{2016}$

+ Mặt khác:

Câu 18:

Cho số phức z thỏa mãn |z – 1 – 2i| = 2. Giá trị lớn nhất của T = |z| + |z – 3 – 6i| gần với giá trị nào nhất?

A. 6

B. 7

C. 8

D. 9

Xem đáp án

Chọn C.

Ta có |z|² = |(z – 1 – 2i) + (1 + 2i)|² = |z – 1- 2i|² + |1 + 2i|² + 2(z – 1 – 2i)(1 + 2i) (1)

|z – 3 – 6i|² = |(z – 1 – 2i) – 2(1 + 2i)|² = |z – 1 – 2i|² + 4|1 + 2i|² - 4(z – 1- 2i)(1 + 2i) (2)

Từ (1) và (2) suy ra: 2|z|² + |z – 3- 6i|² = 3|z – 1- 2i|² + 6|1 + 2i|² = 12 + 30 = 42.

Áp dụng bất đẳng thức Bunhiakovsky ta có:

Vậy

Có $3 \sqrt{7} \approx 8 .$

Câu 19:

Cho số phức z thỏa mãn | z -3 - 4i| = $\sqrt{5}$ .Tìm |z| để biểu thức: P = |z + 2|² - |z – i|²đạt giá trị lớn nhất?

B. 10

Xem đáp án

Chọn A.

Gọi M( x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.

Ta có: $\sqrt{5} =$ | z -3 - 4i| = |x + yi - 3 - 4i| = $\sqrt{{(x - 3)}^{2} + {(y - 4)}^{2}}$

Suy ra ${(x - 3)}^{2} + {(y - 4)}^{2} = 5$

Biểu diễn hình học của P là đường thẳng và P = 4x + 2y + 3.

Áp dụng bất đẳng thức Bunyakovsky ta có:

P = 4x + 2y + 3 = 4(x – 3) + 2(y – 4) + 23

Vậy MaxP = 33 khi và chỉ khi $\{\begin{array}{l} 4 x + 2 y + 3 = 33 \\ {(x - 3)}^{2} + {(y - 4)}^{2} = 5 \end{array} \Leftrightarrow \{\begin{cases} x = 5 \\ y = 5 \end{cases}$

Do đó: $|z| = 5 \sqrt{2}$

Câu 20:

Tìm mô-đun của số phức w = b + ci biết số phức 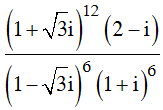là nghiệm của phương trình z²+ 8bz + 64c = 0

A. $2 \sqrt{5}$

B. 7

C. $\sqrt{29}$

D. $\sqrt{19}$

Xem đáp án

Chọn C.

+ Ta có

Do đó

Theo giả thiết ta có ( 8 + 16i) ²+ 8b( 8 + 16i) + 64c = 0

Tương đương: ( 1 + 2i) ²+ b( 1 + 2i) + c = 0

Hay ( 2b + 4)i + b + c – 3 = 0

Ta có hệ $\{\begin{array}{l} 2 b + 4 = 0 \\ b + c - 3 = 0 \end{array} \Leftrightarrow \{\begin{cases} b = - 2 \\ c = 5 \end{cases}$

Khi đó:

Câu 21:

Cho a,b,c là 3 số phức phân biệt khác 0 và modul của chúng bằng nhau .Nếu một nghiệm của phương trình az²+ bz + c = 0 có môđun bằng 1 thì khẳng định nào sau đây đúng.

A. c²= ab

B. a²= bc

C. b = ac

D. b²= ac

Xem đáp án

Chọn D.

Giả sử z₁; z₂ là nghiệm của phương trình đã cho với | $z_{1}$ | = 1.

Theo định lý Viet ta có .Suy ra

Bởi vì , suy ra

Câu 22:

Cho số phức z thỏa mãn là số thuần ảo. Tập hợp các điểm M biểu diễn số phức z là:

A. Đường tròn tâm O, bán kính R = 1.

B. Hình tròn tâm O, bán kính R = 1 (kể cả biên).

C. Hình tròn tâm O, bán kính R = 1 (không kể biên).

D. Đường tròn tâm O, bán kính R = 1 bỏ đi một điểm (0;1).

Xem đáp án

Chọn D.

Gọi M(a ; b) là điểm biểu diễn số phức z = a + bi

Ta có:

Để là số thuần ảo thì

Tập hợp các điểm M là đường tròn tâm O, bán kính R = 1 bỏ đi một điểm (0; 1).

Câu 23:

Cho số phức z thỏa mãn điều kiện |z – 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích

A. S = 9π.

B. S = 12π.

C. S = 16π.

D. S = 25π.

Xem đáp án

Chọn C.

Giả sử w = x + yi , khi đó ( 1) tương đương ( x - 7) ²+ ( y + 9) ²≤ 16

Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I(7; -9), bán kính r = 4

Vậy diện tích cần tìm là S = π.4² = 16π.

Câu 24:

Trong mặt phẳng phức Oxy, tâp hợp các điểm biểu diễn số phức z sao cho z² là số thuần ảo là hai đường thẳng d₁; d₂. Góc α giữa 2 đường thẳng d₁; d₂ là bao nhiêu?

A. α = 45⁰.

B. α = 60⁰.

C. α = 90⁰.

D. α = 30⁰.

Xem đáp án

Chọn C.

Gọi M(x; y) là điểm biểu diễn số phức z = x + yi

Ta có: z²= ( x²- y²) + 2xyi là số thuần ảo khi và chỉ khi x²- y²= 0

Hay y = ± x.

Tập hợp các điểm biểu diễn số phức z thỏa mãn đề bài nằm trên 2 đường thẳng trên và 2 đường thẳng này vuông góc với nhau (vì tích hai hệ số góc bằng -1).

Câu 25:

Tập hợp các điểm biểu diễn số phức z thỏa mãn |z + 2| + |z – 2| = 5 trên mặt phẳng tọa độ là một

A. đường thẳng.

B. đường tròn.

C. elip.

D. hypebol.

Xem đáp án

Chọn C.

Trên mặt phẳng tọa độ Oxy , gọi M(x; y) biểu diễn số phức z = x + yi.

Ta có |z + 2| + |z – 2| = 5

Đặt F₁( -2; 0) ; và F₂( 2; 0) khi đó ( 1) trở thành MF₁+ MF₂= 5

suy ra M nằm trên Elip có hai tiêu điểm là F₁; F₂ và bán kính trục lớn là 5/2.

Phương trình của elip đó là .

CHỌN BỘ SÁCH BẠN MUỐN XEM

100 câu trắc nghiệm Số phức nâng cao (có đáp án)

100 câu trắc nghiệm Số phức nâng cao-P2 (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương