29 câu hỏi trắc nghiệm thuộc 66 câu trắc nghiệm: Phương trình mặt phẳng có đáp án (P2)

Câu 1:

Trong không gian Oxyz, cho hai vectơ $\vec{u}$ = (-1; 3; 4), $\vec{v}$ = (2; -1; 5). Tích có hướng của hai vectơ $\vec{u}$ và $\vec{v}$ là:

A. $[\vec{u}, \vec{v}] = (19; 13; - 5)$

B. $[\vec{u}, \vec{v}] = (19; - 13; - 5)$

C. $[\vec{u}, \vec{v}] = (- 19; 13; - 5)$

D. $[\vec{u}, \vec{v}] = (19; 13; 5)$

Xem đáp án

Đáp án A

Hai vectơ $\vec{u}$ = (-1; 3; 4), $\vec{v}$ = (2; -1; 5)

Thì tích có hướng của hai vectơ $\vec{u}$ và $\vec{v}$ là:

[ $\vec{u}$ , $\vec{v}$ ] = (19; 13; -5)

Câu 2:

Trong không gian Oxyz, cho mặt phẳng (P) đi qua ba điểm A(1;1;1), B(2;3;-1), C(0;3;-2). Một vectơ pháp tuyến của mặt phẳng (P) là:

A. $\vec{n_{p}} = (2; 5; - 4)$

B. $\vec{n_{p}} = (2; - 5; 4)$

C. $\vec{n_{p}} = (- 2; - 5; 4)$

D. $\vec{n_{p}} = (2; - 5; - 4)$

Xem đáp án

Đáp án D

Từ giả thiết ta suy ra

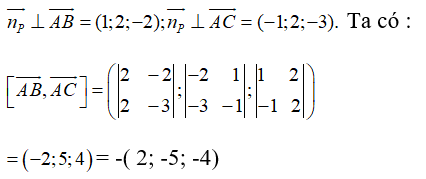
Từ đó suy ra $\vec{n_{p}}$ = (2; -5; -4) là một vectơ pháp tuyến của (P)

Câu 3:

Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1;0;1), B(0;-1;-3), C(2;1;3)

A. x - y - 1 = 0

B. x - y + 1 = 0

C. x + z - 2 = 0

D. x + y - 1 = 0

Xem đáp án

Đáp án A

Từ giả thiết ta suy ra:

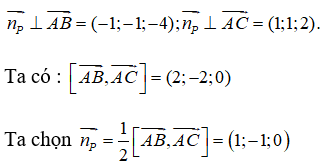
Từ đó suy ra phương trình của mặt phẳng (P) là: 1(x - 1) - 1(y - 0) = 0 ⇔ x - y - 1 = 0

Câu 4:

Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2;1;3), vuông góc với mặt phẳng (Q): x + y - 3z = 0 đồng thời (P) song song với trục Oz

A. x + y - 3 = 0

B. x - y - 1 = 0

C. 2x + y + 3z - 1 = 0

D. x - y + 1 = 0

Xem đáp án

Đáp án B

Từ giả thiết ta suy ra:

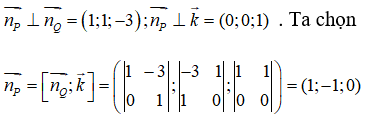
Mặt khác mặt phẳng (P) đi qua điểm A(2;1;3) nên ta có phương trình của mặt phẳng (P) là: 1(x- 2) - 1(y - 1) = 0 ⇔ x - y - 1 = 0

Câu 5:

Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(2;6;-3) và vuông góc với hai mặt phẳng (Oxy), (Oyz) là:

A. 2x - 4 = 0

B. y - 6 = 0

C. z + 3 = 0

D. 2x - 6y - 3z - 49 = 0

Xem đáp án

Đáp án B

Vì (P) vuông góc với hai mặt phẳng (Oxy), (Oyz) và (Oxy) $\cap$ (Oyz) = Oy nên ta có (P) $⊥$ Oy => $\vec{n_{p}} = \vec{j}$ = (0; 1; 0)

Từ đó suy ra phương trình của mặt phẳng (P) là: 0(x - 2) + 1(y - 6 ) + 0(z + 3) = 0 ⇔ y - 6 = 0

Câu 6:

Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm B(2;1;3) đồng thời vuông góc với hai mặt phẳng (Q): x + y - 3z = 0, (R): 2x - y - z = 0

A. 4x + 5y + 3z + 22 = 0

B. 4x - 5y + 3z - 12 = 0

C. 2x + y + 3z - 22 = 0

D. 4x + 5y + 3z - 22 = 0

Xem đáp án

Đáp án D

Từ giả thiết suy ra:

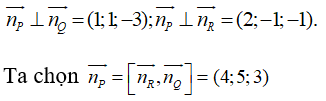
Mặt khác mặt phẳng (P) đi qua điểm B(2 ;1 ;3) nên ta có phương trình của mặt phẳng (P) là:

4(x - 2) + 5(y - 1) + 3(z - 3) = 0 ⇔ 4x + 5y + 3z - 22 = 0

Câu 7:

Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua hai điểm A(1;0;1), B(2;1;3), đồng thời vuông góc với mặt phẳng (Q): x + y - 3z = 0

A. x - y - 1 = 0

B. x + y - 1 = 0

C. x + z - 1 = 0

D. x + y - 3z + 2 = 0

Xem đáp án

Đáp án A

Từ giả thiết suy ra:

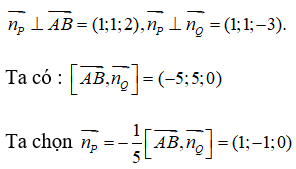
Từ đó suy ra phương trình của mặt phẳng (P) là:

1(x - 1) - 1(y - 0) + 0(z - 1) = 0 ⇔ x - y - 1 = 0

Câu 8:

Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(1;0;1) và chứa trục Ox

A. x - 1 = 0

B. y = 0

C. z - 1 = 0

D. x + z - 1 = 0

Xem đáp án

Đáp án B

Từ giả thiết suy ra

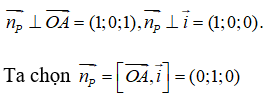
Từ đó suy ra phương trình của mặt phẳng (P) là: 1(y - 0) = 0 ⇔ y = 0

Câu 9:

Trong không gian Oxyz, cho mặt phẳng (P) có phương trình x + ( $m^{2}$ - 2m)y + (m - 1)z + $m^{2}$ + m = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) song song với trục Oy?

A. m = 0

B. m = 2

C. m = 0 hoặc m = 2

D. m = 1

Xem đáp án

Đáp án B

Ta có $\vec{n_{p}}$ = (1; $m^{2}$ - 2m; m - 1). Mặt phẳng (P) song song với trục Oy khi và chỉ khi

Câu 10:

Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 2x - 3y + (2m - 4)z + $m^{2}$ - m = 0, trong đó m là tham số. Với những giá trị nào của m thì (P) song song với trục Oz?

A. m = 2

B. m = 0

C. m = 1

D. Không tồn tại m

Xem đáp án

Đáp án A

Mặt phẳng (P) song song với trục Oz khi và chỉ khi

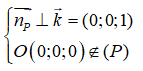
Mà $\vec{n_{p}}$ = (2; -3; 2m - 4) nên: 2.0 + (-3).0 + (2m - 4). 1 = 0

Hay 2m - 4 = 0 nên m = 2

Lại có: $m^{2} - m \neq 0 h a y \{\begin{cases} m \neq 0 \\ m \neq 1 \end{cases}$

Vậy m = 2.

Câu 11:

Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x + my + (m + 3)z + 1 = 0;

x - y + 2z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) vuông góc với mặt phẳng (Q)?

A. m = -1

B. m = 0

C. m = -7

D. Không tồn tại m

Xem đáp án

Đáp án C

Ta có: $\vec{n_{p}}$ = (1; m; m + 3), $\vec{n_{Q}}$ = (1; -1; 2).

Hai mặt phẳng (P) và (Q) vuông góc khi và chỉ khi $\vec{n_{p}}$ . $\vec{n_{Q}}$ = 0

⇔ 1.1 + m.(-1) + (m + 3).2 = 0 ⇔ m + 7 = 0 ⇔ m = -7

Câu 12:

Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x - y + 2z = 0; 2x - 2y + ( $m^{2}$ + 3m)z + $m^{2}$ - m = 0, trong đó m là tham số. Với những giá trị nào của m thì hai mặt phẳng (P) và (Q) song song?

A. m = 1

B. m = -4

C. m = 1 hoặc m = -4

D. m = 0

Xem đáp án

Đáp án B

Vecto pháp tuyến của hai mặt phẳng (P) và (Q) là :

$\vec{n_{p}}$ (1; -1; 2); $\vec{n_{q}}$ (2; -2; m² + 3m)

Hai mặt phẳng (P) và (Q) song song với nhau khi và chỉ khi tồn tại một số thực k sao cho:

$\vec{n_{p}}$ = k. $\vec{n_{q}}$

Câu 13:

Trong không gian Oxyz, cho ba mặt phẳng (P), (Q), (R) lần lượt có phương trình là ( $m^{2}$ + m)x - (m + 2)y + z = 0; x + y + z = 0; 2x + y - z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R)?

A. m = 1

B. m = -1

C. m = $\frac{- 3}{2}$

D. m = $\frac{- 3}{2}$ hoặc m = -1

Xem đáp án

Đáp án A

Ta có:

Mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R) khi và chỉ khi

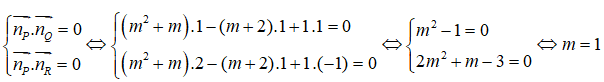
Câu 14:

Trong không gian Oxyz, cho hai mặt phẳng -mx + 3y + 2z + m - 6 = 0 và -2x + (5m + 1)y + (m + 3)z - 10 = 0. Hai mặt phẳng này cắt nhau khi và chỉ khi:

A. m ≠ -4

B. m ≠ $\frac{- 6}{5}$

C. m ≠ 1

D. Mọi m

Xem đáp án

Đáp án C

Gọi hai mặt phẳng đã cho lần lượt là (P) và (Q). Ta có

Hai vectơ này song song khi và chỉ khi m - 6 $\neq$ -10 hay m $\neq$ -4 và tồn tại một số thực k sao cho

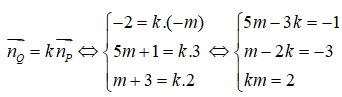
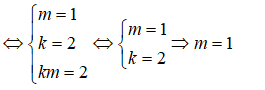(thỏa mãn)

Từ đó suy ra hai mặt phẳng (P) và (Q) cắt nhau khi và chỉ khi hai vectơ pháp tuyến của chúng không song song, điều đó tương đương với m khác 1.

Câu 15:

Trong không gian Oxyz, hai mặt phẳng 3x + 2y - mz + 2m - 7 = 0 và (5m + 1)x + (m + 3)y - 2z - 10 = 0. Trùng nhau khi và chỉ khi:

A. m = -4

B. m = $\frac{- 6}{5}$

C. m = 1

D. Không có giá trị nào của m thỏa mãn

Xem đáp án

Đáp án C

Hai mặt phẳng 3x + 2y - mz + 2m - 7 = 0 và (5m + 1)x + (m + 3)y - 2z - 10 = 0 trùng nhau khi và chỉ khi tồn tại một số thực k sao cho:

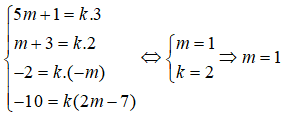
Câu 16:

Trong không gian Oxyz, cho điểm A(1;2;-3) và mặt phẳng (P) có phương trình x - 2y + 2z + 1 = 0. Khoảng cách từ A đến mặt phẳng (P) là:

A. $\frac{8}{3}$

B. $- \frac{8}{3}$

C. $\frac{8}{9}$

D. $8$

Xem đáp án

Đáp án A

Câu 17:

Trong không gian Oxyz, cho hai mặt phẳng song song (P): 4x - 3y - 8 = 0 và (Q): 8x - 6y - 1 = 0. Khoảng cách giữa hai mặt phẳng (P) và (Q) là:

A. $\frac{15}{100}$

B. $\frac{3}{2}$

C. $\frac{15}{\sqrt{101}}$

D. $\frac{15}{\sqrt{28}}$

Xem đáp án

Đáp án B

Lấy một điểm M(2 ;0 ;0)∈(P). Vì hai mặt phẳng (P) và (Q) song song nên ta có:

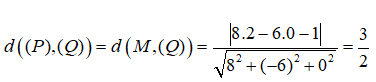
Câu 18:

Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng tọa độ (Oxy) và (Oxz) là hai mặt phẳng có phương trình:

A. y + z = 0 và y - z = 0

B. x + y = 0 và x - y = 0

C. x + z = 0 và x - z = 0

D. y + 2z = 0 và y - 2z = 0

Xem đáp án

Đáp án A

Phương trình của hai mặt phẳng (Oxy) và (Oxz) lần lượt là z = 0 và y = 0.

Điểm M(x ;y ;z) cách đều hai mặt phẳng đó khi và chỉ khi

Câu 19:

Trong không gian Oxyz, tập hợp các điểm cách đều hai mặt phẳng (P): x + 3y - 4z + 1 = 0 và (Q): x + 3y - 4z + 7 = 0 là:

A. x + 3y - 4z + 8 = 0

B. x + 3y - 4z + 6 = 0

C. x + 3y - 4z + 4 = 0

D. x + 3y - 4z - 6 = 0

Xem đáp án

Đáp án C

Điểm M(x,y,z) cách đều hai mặt phẳng (P) và (Q) khi và chỉ khi

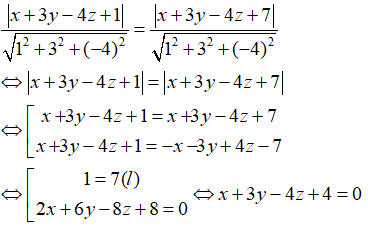
Câu 20:

Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng (P): 2x + 3y + z - 1 = 0 và (Q): 3x + y + 2z - 3 = 0 là hai mặt phẳng có phương trình là:

A. x - 2y + z - 2 = 0 và 5x + 4y + 4z - 4 = 0

B. x - 2y + z - 2 = 0 và 5x + 4y + 3z - 4 = 0

C. x - 3y + z - 2 = 0 và 5x + 4y + 3z - 4 = 0

D. x + 2y + z - 2 = 0 và 5x + 4y + 3z - 4 = 0

Xem đáp án

Đáp án B

Điểm M(x,y,z) cách đều hai mặt phẳng (P) và (Q) khi và chỉ khi:

d(M ; (P)) = d(M ; (Q))

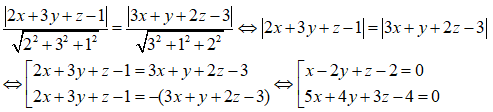
Câu 21:

Trong không gian Oxyz, biết rằng trục Ox song song với mặt phẳng (P): y + z - 1 = 0. Khoảng cách giữa Ox và mặt phẳng (P) là:

A. 1

B. $\frac{1}{2}$

C. $- \frac{1}{\sqrt{2}}$

D. $\frac{1}{\sqrt{2}}$

Xem đáp án

Đáp án D

Vì Ox song song với mặt phẳng (P) và O thuộc Ox nên ta có:

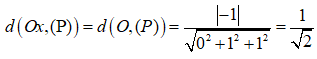
Câu 22:

Trong không gian Oxyz, cho điểm A(1 ;-2 ;3) và mặt phẳng (P) có phương trình x + 2y - 2z + m = 0. Tìm các giá trị của m, biết rằng khoảng cách từ A đến mặt phẳng (P) bằng 1

A. m = 12

B. m = 18

C. m = 18 hoặc m = 0

D. m = 12 hoặc m = 6

Xem đáp án

Đáp án D

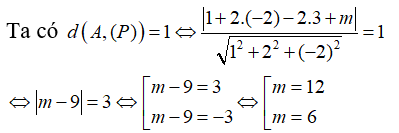
Câu 23:

Trong không gian Oxyz, cho hai mặt phẳng: (P): x - 2y - 2z + 1 = 0, (Q): 2x - 4y - 4z + m = 0. Tìm các giá trị của m biết rằng khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 1

A. m = 8

B. m = 38

C. m = 8 hoặc m = -4

D. m = 38 hoặc m = -34

Xem đáp án

Đáp án C

Lấy A(-1; 0; 0) ∈ (P). Ta có

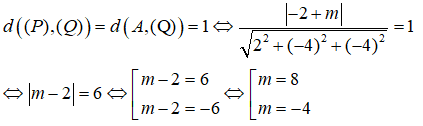
Câu 24:

Trong không gian Oxyz, cho điểm A di động trên mặt phẳng (P): 2x - y - 2z = 0, điểm B di động trên mặt phẳng (Q): 4x - 2y - 4z - 9 = 0. Khoảng cách giữa hai điểm A và B nhỏ nhất là:

A. $\frac{3}{2}$

B. $\frac{1}{4}$

C. $\frac{9}{\sqrt{28}}$

D. $\frac{9}{28}$

Xem đáp án

Đáp án A

Khoảng cách nhỏ nhất giữa hai điểm A và B chính là khoảng cách giữa hai mặt phẳng (P) và (Q), dấu bằng xảy ra khi và chỉ khi AB vuông góc với (P). Mặt khác vì O thuộc (P) nên ta có:

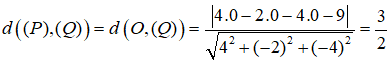
Vậy khoảng cách giữa hai điểm A và B nhỏ nhất bằng $\frac{3}{2} .$

Câu 25:

Trong không gian Oxyz, cho mặt phẳng (P): x - 2y + 3z + 1 = 0 và mặt cầu (S): $x^{2} + y^{2} + z^{2}$ - 2x - 4y + 6z + 5 = 0. Khẳng định nào dưới đây là đúng?

A. (P) giao (S) theo một đường tròn

B. (P) tiếp xúc với (S)

C. (P) không cắt (S)

D. Cả ba khẳng định trên đều sai

Xem đáp án

Đáp án A

Mặt cầu (S) có tâm I(1; 2; -3) và có bán kính là

Do đó mặt phẳng (P) giao với mặt cầu (S) theo một đường tròn.

Câu 26:

Trong không gian Oxyz, cho mặt phẳng (P): 2x - 2y + z + 1 = 0 và mặt cầu (S): $x^{2} + y^{2} + z^{2}$ + 2x + 4y - 6z + 10 = 0. Khẳng định nào dưới đây là đúng?

A. (P) và (S) có vô số điểm chung

B. (P) tiếp xúc với (S)

C. (P) không cắt (S)

D. Cả ba khẳng định trên đều sai

Xem đáp án

Đáp án B

Câu 27:

Trong không gian Oxyz, cho mặt cầu (S): ${(x - 2)}^{2} {+ (y + 1)}^{2} {+ (z + 2)}^{2}$ = 4 và mặt phẳng (P): 4x - 3y + m = 0. Với những giá trị nào của m thì mặt phẳng (P) và mặt cầu (S) có đúng một điểm chung?

A. m = -1

B. m = 9 hoặc m = -31

C. m = 1 hoặc m = 21

D. m = -1 hoặc m = -21

Xem đáp án

Đáp án D

Mặt cầu (S) có tâm I(2;-1;-2) và có bán kính R=2. Mặt phẳng (P) và mặt cầu (S) có đúng một điểm chung khi và chỉ khi (P) tiếp xúc với (S), từ đó ta được: