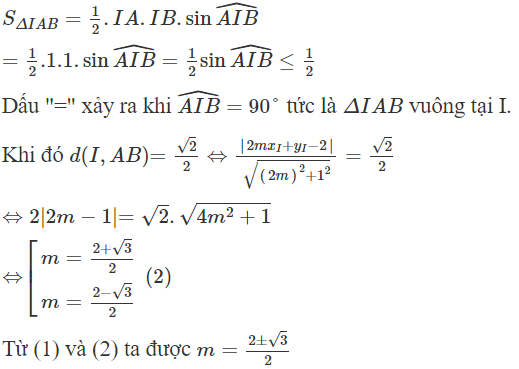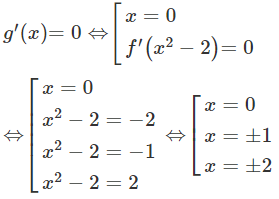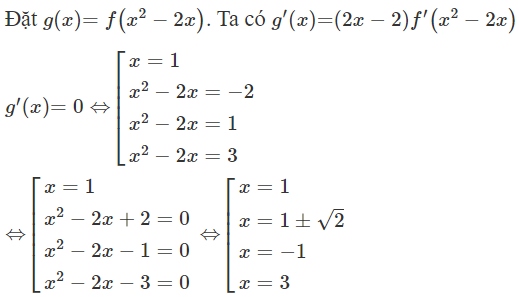10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Cực trị của hàm số có đáp án (P2) (Vận dụng)

Trắc nghiệm Cực trị của hàm số có đáp án (Vận dụng)

Trắc nghiệm Cực trị của hàm số có đáp án (P2) (Vận dụng)

1226 lượt thi
10 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hàm số y = f(x) có đạo hàm liên tục trên $ℝ$ . Đồ thị hàm số y = f'(x) như hình vẽ sau:

Số điểm cực trị của hàm số $y = f (x) - 4 x$ là

A. 2

B. 3

C. 4

D. 1

Xem đáp án

Đáp án D

Đặt: $g (x) = f (x) - 4 x$

Ta có: $g^{'} (x) = f^{'} (x) - 4, g^{'} (x) = 0 \Leftrightarrow f^{'} (x) = 4$

Dựa vào đồ thị, suy ra phương trình $f^{'} (x) = 4$ có 2 nghiệm $x_{1}; x_{2}$ trong đó $x_{1} = - 1$ là nghiệm kép và $x_{2} > 1$ là nghiệm đơn.

$\Rightarrow$ Phương trình $g^{'} (x) = 0$ có 2 nghiệm $x_{1}; x_{2}$ nhưng $g^{'} (x)$ đổi dấu duy nhất 1 lần khi qua nghiệm $x_{2}$ này. Vậy hàm số $y = f (x) - 4 x$ có một điểm cực trị.

Câu 2:

Tìm m đề đồ thị hàm số $y = x^{4} - 2 m x^{2} + 1$ có ba điểm cực trị $A (0; 1), B, C$ thỏa mãn BC = 4

A. m = $\sqrt{2}$

B. m = 4

C. m = ±4

D. m = $\pm \sqrt{2}$

Xem đáp án

Đáp án B

Tập xác định: $D = ℝ$

$y' = 4 x^{3} - 4 m x = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x^{2} = m \end{array}$

Hàm số đã cho có ba điểm cực trị $\Leftrightarrow m > 0$

Tọa độ điểm cực trị của đồ thị hàm số:

$A (0; 1), B (\sqrt{m}; - m^{2} + 1), C (- \sqrt{m}; - m^{2} + 1)$

Theo giả thiết $B C = 4 \Leftrightarrow 4 m = 16 \Leftrightarrow m = 4$ ( thỏa mãn).

Câu 3:

Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y = x^{4} - 2 (m + 1) x^{2} + m^{2}$ có ba điểm cực trị tạo thành một tam giác vuông cân

A. m = 0

B. m = -1, m = 0

C. m = 1

D. m = 1, m = 0

Xem đáp án

Đáp án A

Cách 1: PP tự luận

Ta có $y^{'} = 4 x (x^{2} - m - 1)$

Xét $y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x^{2} = m + 1 \end{array}$ . Để đồ thị số có ba điểm cực trị thì $m > - 1$

Tọa độ ba điểm cực trị là $A (0; m^{2}), B (\sqrt{m + 1}; - 2 m - 1), C (- \sqrt{m + 1}; - 2 m - 1)$

Gọi H là trung điểm của đoạn thẳng BC thì $H (0; - 2 m - 1)$

Khi đó ba điểm cực trị lập thành tam giác vuông cân khi $A H = B H$

$\Leftrightarrow \sqrt{{(m + 1)}^{4}} = \sqrt{m + 1} \Leftrightarrow {(m + 1)}^{4} = m + 1 \Leftrightarrow [\begin{array}{l} m = 0 (t m) \\ m = - 1 (k t m) \end{array}$

Câu 4:

Cho hàm số y = f(x) có đúng ba điểm cực trị là $x = - 2, x = - 1, x = 2$ và có đạo hàm liên tục trên $ℝ$ .Khi đó hàm số $y = f (x^{2} - 2)$ có bao nhiêu điểm cực trị?

A. 5

B. 8

C. 6

D. 4

Xem đáp án

Đáp án A

Vì hàm số y = f(x) có đúng ba điểm cực trị là x = -2, x = -1, x = 2

và có đạo hàm liên tục trên $ℝ$ nên f'(x) = 0 có ba nghiệm là x = -2, x = -1, x = 2 (ba nghiệm bội lẻ).

Xét hàm số $g (x) = f (x^{2} - 2)$ có $g^{'} (x) = 2 x . f^{'} (x^{2} - 2)$

$g^{'} (x) = 2 x . f^{'} (x^{2} - 2)$

Câu 5:

Gọi S là tập chứa tất cả các giá trị nguyên của m sao cho hàm số $y = x^{4} - 2 (m - 1) x^{2} + m^{2} - m$ có ba điểm cực trị lập thành một tam giác vuông. Tổng tất cả các phần tử của tập S bằng

A. 2

B. 3

C. -5

D. 1

Xem đáp án

Đáp án A

Tập xác định $D = ℝ$

$y^{'} = 4 x^{3} - 4 (m - 1) x; y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x^{2} = m - 1 \end{array}$

Hàm số có ba cực trị khi và chỉ khi $m > 1 (*)$

Với điều kiện $(*)$ , đồ thị hàm số có ba điểm cực trị là $A (0; m^{2} - m)$ , $B (\sqrt{m - 1}; m - 1)$ , $C (- \sqrt{m - 1}; m - 1)$ .

Ta có $\vec{A B} = (\sqrt{m - 1}; - m^{2} + 2 m - 1)$ , $\vec{A C} = (- \sqrt{m - 1}; - m^{2} + 2 m - 1)$

Câu 6:

Cho hàm số y = f(x) có đạo hàm trên $ℝ$ và có bảng xét dấu f'(x) như sau

Hỏi hàm số $y = f (x^{2} - 2 x)$ có bao nhiêu điểm cực tiểu?

A. 4

B. 2

C. 3

D. 1

Xem đáp án

Đáp án D

Trong đó các nghiệm -1, 1, 3 là nghiệm bội lẻ và $1 \pm \sqrt{2}$ là nghiệm bội chẵn.

Vì vậy hàm số g'(x) chỉ đổi dấu khi đi qua các nghiệm -1, 1, 3.

Ta có $g^{'} (0) = - 2 f^{'} (0) < 0$ (do $f^{'} (0) > 0$ ).

Bảng xét dấu g'(x)

Vậy hàm số $y = f (x^{2} - 2 x)$ có đúng 1 điểm cực tiểu là x = 1

Câu 7:

Cho hàm số bậc bốn y = f(x) có đồ thị như hình bên dưới. Số điểm cực trị của hàm số $g (x) = f (- x^{3} + 3 x)$ là

A. 9

B. 3

C. 7

D. 5

Xem đáp án

Đáp án A

Ta có $g^{'} (x) = (- 3 x^{2} + 3) f^{'} (- x^{3} + 3 x)$ ;

$g^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} - 3 x^{2} + 3 = 0 (1) \\ f^{'} (- x^{3} + 3 x) = 0 (2) \end{array}$

$(1) \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 1 \end{array}$ ;

$(2) \Leftrightarrow [\begin{array}{l} - x^{3} + 3 x = a (a < - 2) \\ - x^{3} + 3 x = b (- 2 < b < 0) \\ - x^{3} + 3 x = c (0 < c < 2) \end{array}$

Xét hàm số $h (x) = - x^{3} + 3 x$

Câu 8:

Cho hàm số bậc năm y = f(x) liên tục trên $ℝ$ và có đồ thị hàm số $y = f^{'} (x)$ như trong hình bên. Tìm số điểm cực đại của hàm số $y = e^{f (x)} . π^{f^{3} (x)}$

A. 1

B. 0

C. 2

D. 3

Xem đáp án

Đáp án C

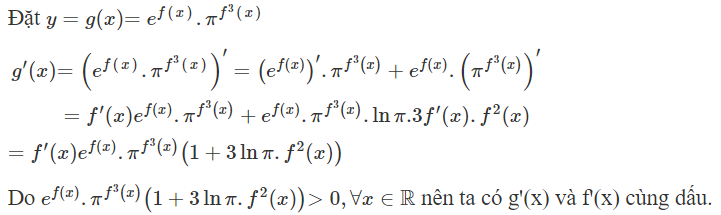
Dựa vào đồ thị hàm số y = f'(x) ta suy ra dấu của g'(x) từ đó có bảng biến thiên của hàm số đã cho như sau

Từ bảng biến thiên ta suy ra hàm số đã cho có 2 điểm cực đại.

Câu 9:

Cho hàm số bậc ba y = f(x) có đồ thị như trong hình vẽ bên. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số $y = f (|x| + m - 2020)$ có 5 điểm cực trị ?

A. 2024

B. 2022

C. 2020

D. 2018

Xem đáp án

Đáp án B

Đặt: $g (x) = f (|x| + m - 2020)$ . Ta có: $g (x) = g (- x)$ , do vậy hàm số $y = g (x)$ có đồ thị đối xứng qua trục tung.

Để g(x) có điểm cực trị trên $ℝ$ , khi đó ta chỉ cần xét hàm g(x) với $x \geq 0$ có hai điểm cực trị có hoành độ $0 < x_{1} < x_{2}$

Ta có $g' (x) = f' (x + m - 2020)$ , suy ra

$g' (x) = 0 \Leftrightarrow [\begin{array}{l} x + m - 2020 = 3 \\ x + m - 2020 = 5 \end{array} \Leftrightarrow [\begin{array}{l} x = 2023 - m = x_{1} \\ x = 2025 - m = x_{2} \end{array}$

Vậy $0 < x_{1} < x_{2} \Leftrightarrow 0 < 2023 - m \Leftrightarrow m < 2023$

Câu 10:

Tìm tất cả các giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số $y = x^{3} - 3 m x + 2$ cắt đường tròn (C) tâm I(1;1), bán kính bằng 1 tại hai điểm phân biệt A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất?

A. $m = \frac{2 \pm \sqrt{3}}{3}$

B. $m = \frac{1 \pm \sqrt{3}}{2}$

C. $m = \frac{2 \pm \sqrt{3}}{2}$

D. $m = \frac{2 \pm \sqrt{5}}{2}$

Xem đáp án

Đáp án C

$y^{'} = 3 x^{2} - 3 m$

Hàm số có hai điểm cực trị khi $m > 0 (1)$

Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = x^{3} - 3 m x + 2$ có phương trình

$y = - 2 m x + 2 \Leftrightarrow 2 m x + y - 2 = 0$

Diện tích tam giác IAB là

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Cực trị của hàm số có đáp án (Vận dụng)

Trắc nghiệm Cực trị của hàm số có đáp án (P2) (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương