Trắc nghiệm Cực trị của hàm số có đáp án (P1) (Vận dụng)
-
1433 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số . Đặt . Để đồ thị hàm số có điểm cực đại thì tổng giá trị của A + 2B là:
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
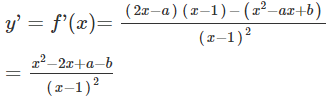
Vì C (0; -1) là điểm cực đại của đồ thị hàm số nên:
Thay a = 1, b = 1 ào hàm số ta thấy điểm C (0; - 1) là điểm cực đại của đồ thị hàm số.
Vậy
Câu 2:
Cho hàm số bậc hai y = f(x) có đồ thị như hình vẽ bên, một hàm số g (x) xác định theo f (x) có đạo hàm . Tìm tất cả các giá trị thực của tham số m để hàm số g (x) không có cực trị.
 Xem đáp án
Xem đáp án
Đáp án B
Gọi hàm số
Đồ thị hàm số nhận điểm (0; - 1) làm đỉnh và đi qua điểm (1; 1) nên hay
Do đó
Hàm số không có cực trị vô nghiệm hoặc có nghiệm kép.
Vậy
Câu 3:
Cho hàm bậc bốn y = f(x). Hàm số y = f'(x) có đồ thị như hình bên. Số điểm cực đại của hàm số là:
 Xem đáp án
Xem đáp án
Đáp án A
Quan sát đồ thị hàm số ta thấy

Nghiệm của phương trình (1) là nghiệm bội 2 nên không là cực trị của hàm số
Lập BBT của hàm số y = g(x):
Dựa vào BBT ta thấy hàm số đạt cực đại tại x = - 1
Câu 4:
Điểm thuộc đường thẳng cách đều hai điểm cực trị của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Suy ra tọa độ hai điểm cực trị của đồ thị hàm số là
Gọi khi đó
Mà M cách đều A, B
Suy ra
Câu 5:
Khoảng cách từ điểm cực tiểu của đồ thị hàm số đến trục tung bằng:
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Suy ra điểm cực tiểu của đồ thị hàm số là M (2; - 2)
Vậy
Câu 6:
Cho hàm số y = f(x) có đồ thị như hình vẽ bên:
Trên đoạn , hàm số đã cho có mấy điểm cực trị?
 Xem đáp án
Xem đáp án
Đáp án D
Dựa vào đồ thị hàm số ta thấy, trên đoạn , hàm số có 3 điểm cực trị là
Câu 7:
Cho hàm số (với và ) có đồ thị như hình vẽ. Số điểm cực trị của hàm số là:
 Xem đáp án
Xem đáp án
Đáp án B
Từ đồ thị ta thấy, hàm số f (x) đạt cực trị tại các điểm x = - 2 và x = 0 nên
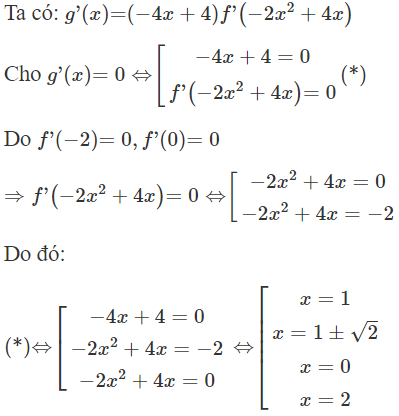
Các nghiệm này đều là nghiệm đơn
Do đó g’(x) đổi dấu qua 5 điểm trên
Vậy hàm số y = g(x) có 5 điểm cực trị
Câu 8:
Cho hàm số f (x) có bảng biến thiên như sau:
Số điểm cực trị của hàm số là:
 Xem đáp án
Xem đáp án
Đáp án C
Đặt ta có
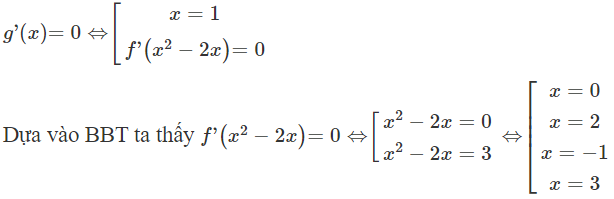
phương trình có 5 nghiệm đơn x = 0, x = 2, x = 3, x = -1, x = 1
Vậy hàm số đã cho có 5 điểm cực trị.
Câu 9:
Số điểm cực trị của hàm số là:
 Xem đáp án
Xem đáp án
Đáp án B
Xét hàm số ta có:
hàm số có 1 cực trị.
Xét phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành ta có:
đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt.
số điểm cực trị của hàm số là: S = 1 + 2 = 3 cực trị.
Có thể theo đồ thị sau:
Câu 10:
Số điểm cực trị của hàm số là:
 Xem đáp án
Xem đáp án
Đáp án A
Xét hàm số
TXĐ: D = R
Ta có:
BBT:
Từ BBT của đồ thị hàm số ta suy ra BBT của đồ thị hàm số như sau:
Từ BBT ta thấy hàm số có 3 điểm cực trị.
Câu 11:
Cho hàm số liên tục trên R đồng thời hàm số có đồ thị như hình vẽ bên, xác định số điểm cực trị của đồ thị hàm số
 Xem đáp án
Xem đáp án
Đáp án B
Từ hình vẽ ta có đồ thị hàm số là một trong hai đồ thị dưới đây:
Từ hai đồ thị trên ta dựng được đồ thị là một trong hai đồ thị dưới đây:
Từ hai đồ thị ở trên ta thấy: Ở cả hai trường hợp thì hàm số đều có 5 điểm cực trị.
Câu 12:
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ
Tìm tất cả các giá trị của m để hàm số có ba điểm cực trị
 Xem đáp án
Xem đáp án
Đáp án A
Đồ thị hàm số có được bằng cách tịnh tiến đồ thị hàm số theo phương của trục Oy m đơn vị (lên trên hay xuống dưới phụ thuộc vào m dương hay âm), do đó nó đồ thị hàm số có
Lấy đối xứng phần dưới của đồ thị hàm số qua Ox ta được đồ thị hàm số
Để đồ thị hàm số có ba điểm cực trị thì
Câu 13:
Số điểm cực đại của hàm số bằng:
 Xem đáp án
Xem đáp án
Đáp án B
Xét phương trình , phương trình có 100 nghiệm phân biệt.
Phương trình là phương trình bậc 100, có 100 nghiệm, do đó hàm số có 99 điểm cực trị.
Lại có nên số điểm cực tiểu nhiều hơn số điểm cực đại là 1
Do đó hàm số có 50 điểm cực tiểu, 49 điểm cực đại.
Câu 14:
Cho hàm số liên tục trên R và có đồ thị như hình vẽ bên. Số điểm cực đại của hàm số là:
 Xem đáp án
Xem đáp án
Đáp án A
Ta có:
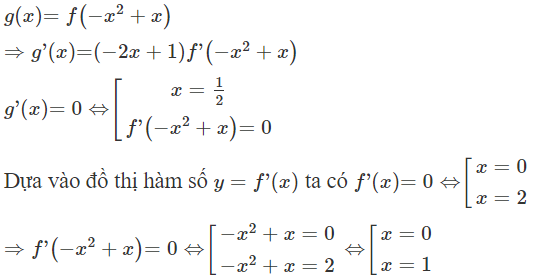
Suy ra phương trình có 3 nghiệm đơn phân biệt
Chọn x = 2 ta có , qua các nghiệm thì đổi dấu
BBT:
Dựa vào BBT ta thấy hàm số có hai điểm cực đại x = 0, x = 1
Câu 15:
Cho hàm số . Hàm số có đồ thị như hình vẽ bên.
Hàm số có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Đáp án A
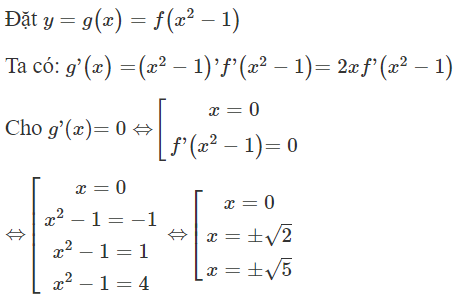
(tất cả các nghiệm trên đều là nghiệm bội lẻ)
Bảng xét dấu :
Vậy hàm số có tất cả 5 điểm cực trị.
