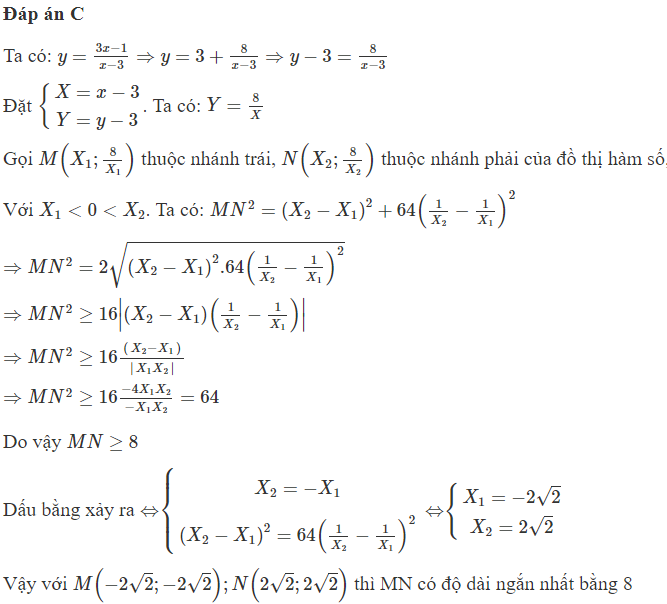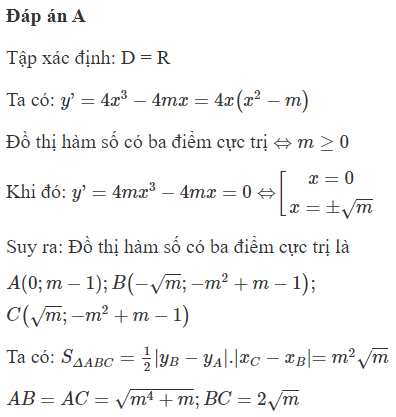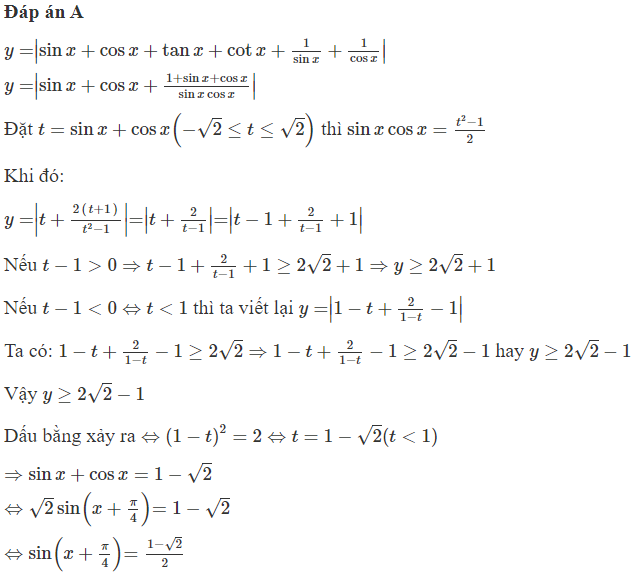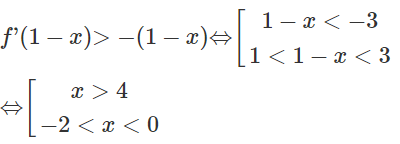30 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án (P2)

Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án

Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án (P2)

3127 lượt thi
30 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

Với mỗi số thực x, gọi f(x) là giá trị nhỏ nhất trong các số $g_{1} (x) = 4 x + 1, g_{2} (x) = x + 2, g_{3} (x) = - 2 x + 4$ . Giá trị lớn nhất của f(x) trên R là:

A. 1/3

B. 2/3

C. 8/3

D. 3

Xem đáp án

Đáp án C

Quan sát các đồ thị hàm số ta thấy: (phía dưới)

+ Trong nửa khoảng $(- \infty; \frac{1}{3}]$ thì $\min \{g_{1} (x), g_{2} (x), g_{3} (x)\} = g_{1} (x)$ nên đồ thị hàm số $y = f (x)$ là nửa đường thẳng $y = g_{1} (x)$

+ Trong đoạn $[\frac{1}{3}; \frac{2}{3}]$ thì $\min \{g_{1} (x), g_{2} (x), g_{3} (x)\} = g_{2} (x)$ nên đồ thị hàm số $y = f (x)$ là một đoạn đường thẳng $y = g_{2} (x)$

+ Trong nửa khoảng $[\frac{2}{3}; + \infty)$ thì $\min \{g_{1} (x), g_{2} (x), g_{3} (x)\} = g_{3} (x)$

Câu 2:

Biết rằng đồ thị của hàm số $y = P (x) = x^{3} - 2 x^{2} - 5 x + 2$ cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là $x_{1}, x_{2}, x_{3}$ . Khi đó giá trị của biểu thức $T = \frac{1}{{x_{1}}^{2} - 4 x_{1} + 3} + \frac{1}{{x_{2}}^{2} - 4 x_{2} + 3} + \frac{1}{{x_{3}}^{2} - 4 x_{3} + 3}$ bằng:

A. $T = \frac{1}{2} [- \frac{P' (1)}{P (1)} + \frac{P' (3)}{P (3)}]$

B. $T = \frac{1}{2} [- \frac{P' (1)}{P (1)} - \frac{P' (3)}{P (3)}]$

C. $T = \frac{1}{2} [\frac{P' (1)}{P (1)} - \frac{P' (3)}{P (3)}]$

D. $T = \frac{1}{2} [\frac{P' (1)}{P (1)} + \frac{P' (3)}{P (3)}]$

Xem đáp án

Đáp án C

Xét biểu thức chia P(x) cho $x^{2} - 4 x + 3$ ta được $P (x) = (x + 2) (x^{2} - 4 x + 3) - 4$

Câu 3:

Cho hàm số y = f(x) có bảng biến thiên như sau:

Đồ thị hàm số $y = |f (x - 2017) + 2018|$ có bao nhiêu điểm cực trị?

A. 2

B. 3

C. 5

D. 4

Xem đáp án

Đáp án B

Do hàm số $y = f (x - 2017) + 2018$ thu được bằng cách tịnh tiến đồ thị hàm số $y = f (x)$ sang phải một đoạn có độ dài bằng 2017 đơn vị và tịnh tiến trên một đoạn có độ dài bằng 2018 đơn vị nên ta có bảng biến thiên của hàm số $y = f (x)$ như sau:

Do đó ta có bảng biến thiên của hàm số $y = |g (x)|$ là:

Vậy đồ thị hàm số $y = |f (x - 2017) + 2018|$ có 3 cực trị

Câu 4:

Cô An đang ở khách sạn A bên bờ biển, cô cần đi du lịch đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C nhất là 50km. Từ khách sạn A, cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy đến hòn đảo C (như hình vẽ). Biết rằng chi phí đi đường thủy là 5USD/km, chi phí đi đường bộ là 3USD/km. Hỏi cô An phải đi đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.

A. 15/2 ( k m )

B. 85/2 ( k m )

C. 50 ( k m )

D. 10 $\sqrt{26}$ ( k m )

Xem đáp án

Vậy cô An phải đi đường bộ một khoảng $A D = 50 - \frac{15}{2} = \frac{85}{2} (k m)$ để chi phí ít nhất.

Câu 5:

Tìm tập hợp S tất cả các giá trị của tham số thực m để đồ thị hàm số $y = x^{4} - 2 m^{2} x^{2} + m^{4} + 3$ có ba điểm cực trị đồng thời ba điểm cực trị đó cùng với gốc tọa độ O tạo thành một tứ giác nội tiếp.

A. $S = \{\frac{- 1}{\sqrt{3}}; 0; \frac{1}{\sqrt{3}}\}$

B. $S = \{- 1; 1\}$

C. $S = \{\frac{- 1}{\sqrt{3}}; \frac{1}{\sqrt{3}}\}$

D. $S = \{\frac{- 1}{\sqrt{2}}; \frac{1}{\sqrt{2}}\}$

Xem đáp án

Đáp án C

$y' = 4 x^{3} - 4 m^{2} x; y' = 0 \Leftrightarrow [\begin{matrix} x = 0 \\ x = \pm m \end{matrix}$

Để hàm số có 3 cực trị thì phương trình y' = 0 có 3 nghiệm hay $m \neq 0$

Không mất ính tổng quát giả sử 3 điểm cực trị có tọa độ $A (0; m^{4} + 3); B (m; 3); C (- m; 3)$

Ta có: $\vec{A C} (- m; - m^{4}); \vec{O C} (- m; 3)$

Tứ giác OBAC có: $\{\begin{matrix} A B = A C \\ O B = O C \end{matrix}$

Suy ra OA là đường trung trực của BC

Để tứ giác OBAC nội tiếp đường tròn thì điểm B, C phải nhìn cạnh OA dưới góc $90^{\circ}$

$90^{\circ}$

Câu 6:

Ông Bình đặt thợ làm một bể cá, nguyên liệu bằng kính trong suốt, không có nắp đậy dạng hình hộp chữ nhật có thể tích chứa được $220500 c m^{3}$ nước. Biết tỉ lệ giữa chiều cao và chiều rộng của bể bằng 3. Xác định diện tích đáy của bể cá để tiết kiệm nguyên vật liệu nhất.

A. 2220 $c m^{2}$

B. 1880 $c m^{2}$

C. 2100 $c m^{2}$

D. 2200 $c m^{2}$

Xem đáp án

Câu 7:

Cho hàm số $y = x^{4} - 2 m x^{2} + m$ có đồ thị (C) với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm m để tiếp tuyến $∆$ với đồ thị (C) tại A cắt đường tròn $(γ) : x^{2} + {(y - 1)}^{2} = 4$ tạo thành một dây cung có độ dài nhỏ nhất

A. 16/13

B. − 13/16

C. 13/16

D. −16/13

Xem đáp án

Đáp án C

Đường tròn $(γ) : x^{2} + {(y - 1)}^{2} = 4$ có tâm $I (0; 1), R = 2$

Ta có: $A (1; 1 - m); y' = 4 x^{3} - 4 m x \Rightarrow y' (1) = 4 - 4 m$

Suy ra phương trình $Δ : y = (4 - 4 m) (x - 1) + 1 - m$

Dễ thấy $∆$ luôn đi qua điểm cố định $F (\frac{3}{4}; 0)$ và điểm F nằm trong đường tròn $(γ)$

Giả sử $∆$ cắt $(γ)$ tại M, N. Thế thì ta có $M N = 2 \sqrt{R^{2} - d^{2} (I; Δ)} = 2 \sqrt{4 - d^{2} (I; Δ)}$

Do đó MN nhỏ nhất $\Leftrightarrow d (I, Δ)$

Câu 8:

Cho hàm số f(x) có đồ thị hàm đường cong (C), biết đồ thị của f'(x) như hình vẽ:

Tiếp tuyến của (C ) tại điểm có hoành độ bằng 1 cắt đồ thị (C ) tại hai điểm A, B phân biệt lần lượt có hoành độ a, b. Chọn khẳng định đúng trong các khẳng định sau:

A. 4 ≥ a − b ≥ − 4

B. a, b ≥ 0

C. a, b < 3

D. $a^{2} + b^{2}$ > 10

Xem đáp án

Đáp án D

Từ đồ thị, ta có $f' (1) = 0$

Phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng 1 có dạng: $y = f' (1) (x - 1) + f (1) \Leftrightarrow y = f (1)$

Phương trình hoành độ giao điểm của tiếp tuyến trên với đồ thị (C): $f (x) = f (1)$

Từ đồ thị, ta có: $f' (- 1) = f' (3) = 0$ . Ta được BBT của hàm số $y = f (x)$

Từ BBT, ta thấy đường thẳng $y = f (1)$ cắt đồ thị hàm số tại ba điểm có hoành độ lần lượt là 1, a, b với a < - 1 và b > 3. Như vậy đáp án D đúng, các khẳng định A, B, C đều không thỏa điều trên.

Câu 9:

Cho hàm số $y = {(x - m)}^{3} - 3 x + m^{2}$ có đồ thị là $(C_{m})$ với m là tham số thực. Biết điểm M(a; b) là điểm cực đại của $(C_{m})$ ứng với một giá trị m thích hợp, đồng thời là điểm cực tiểu của $(C_{m})$ ứng với một giá trị khác của m. Tổng $S = 2018 a + 2020 b$ bằng:

A. 504

B. -504

C. 12504

D. 5004

Xem đáp án

Đáp án A

Vì điểm M(a; b) thuộc đồ thị $(C_{m})$ nên ta có: ${(a - m)}^{3} - 3 a + m^{2} = b, \forall m \in R (1)$

Xét $y' = 3 {(x - m)}^{2} - 3; y' = 0 \Leftrightarrow [\begin{matrix} x = m - 1 \\ x = m + 1 \end{matrix}$

Bảng biến thiên

Dựa vào BBT ta có:

Nếu $m_{1}$ là giá trị của tham số m để đồ thị hàm số nhận điểm M(a; b) là điểm cực đại thì $a = m_{1} - 1$

Nếu $m_{2}$ là giá trị của tham số m để đồ thị hàm số nhận điểm M(a; b) là điểm cực tiểu thì $a = m_{2} + 1$

Do đó $m_{1} = a + 1, m_{2} = a - 1$

Mà $m_{1}, m_{2}$ phải thỏa mãn (1) nên ta có: $\{\begin{matrix} - 1 - 3 a + {(a + 1)}^{2} = b \\ 1 - 3 a + {(a - 1)}^{2} = b \end{matrix} \Leftrightarrow \{\begin{matrix} a = \frac{1}{2} \\ b = - \frac{1}{4} \end{matrix}$

Câu 10:

Gọi d là đường thẳng đi qua A(2;0) có hệ số góc m cắt đồ thị $y = - x^{3} + 6 x^{2} - 9 x + 2$ tại 3 điểm phân biệt A, B, C. Gọi B’, C’ lần lượt là hình chiếu vuông góc của B, C lên trục tung. Tìm giá trị dương của m để hình thang BB’C’C có diện tích bằng 8.

A. m = 3/2

B. m = 1

C. m = 2

D. m = 1/2

Xem đáp án

Để đồ thị hàm số (C) cắt d tại 3 điểm phân biệt thì phương trình (1) phải có 2 nghiệm phân biệt $x \neq 2$

$x \neq 2$

Câu 11:

Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số $y = \frac{x + 1}{\sqrt{m^{2} x^{2} + m - 1}}$ có 4 đường tiệm cận.

A. m > 0

B. Với mọi giá trị của m

C. m < 1 , m ≠ 0 v à m ≠ $\frac{- 1 \pm \sqrt{5}}{2}$

D. m < 1 hoặc m > 1

Xem đáp án

Đáp án C

Với m = 0 thì hàm số không xác định. Do đó $m \neq 0$ (1)

Ta có: $\lim_{x \to + \infty} y = \lim_{x \to + \infty} \frac{x + 1}{\sqrt{m^{2} x^{2} + m - 1}} = \frac{1}{|m|}$ $\Rightarrow$

$\Rightarrow$ đồ thị hàm số có 2 đường tiệm cận ngang.

Để đồ thị hàm số có bốn đường tiệm cận thì cần tìm m để đồ thị hàm số có 2 đường tiệm cận đứng, nghĩa là cần tìm m để phương trình $g (x) = m^{2} x^{2} + m - 1 = 0$ có 2 nghiệm phân biệt khác – 1.

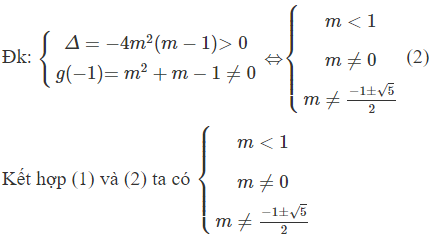
Câu 12:

Cho hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình bên. Đặt $g (x) = f (\sqrt{x^{2} + x + 2})$ . Chọn khẳng định đúng trong các khẳng định sau:

A. g(x) nghịch biến trên khoảng (0;2)

B. g(x) đồng biến trên khoảng (-1;0)

C. g(x) nghịch biến trên khoảng ( − 1/2 ; 0 )

D. g(x) đồng biến trên khoảng ( − ∞ ; − 1 )

Xem đáp án

Đáp án C

Hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d$ ; $f' (x) = 3 a x^{2} + 2 b x + c$ có đồ thị như hình vẽ

Do đó $x = 0 \Rightarrow d = 4; x = 2 \Rightarrow 8 a + 4 b + 2 c + d = 0$ ; $f' (2) = 0 \Leftrightarrow 12 + 4 b + x = 0$ ; $f' (0) = 0 \Leftrightarrow c = 0$

Tìm được $a = 1; b = - 3; c = 0; d = 4$ và hàm số $y = x^{3} - 3 x^{2} + 4$

Ta có:

Câu 13:

Cho hàm số y = f(x) có đạo hàm f'(x) trên R, phương trình f'(x) = 0 có 4 nghiệm thực và đồ thị hàm số f'(x) như hình vẽ. Tìm số điểm cực trị của hàm số $y = f (x^{2})$

A. 3

B. 4

C. 5

D. 6

Xem đáp án

Bảng xét dấu:

Quan sát bảng xét dấu ta thấy: qua 5 điểm $x = 2, x = - 1, x = 0, x = 1, x = 2$ là y; đổi dấu

Vậy hàm số có 5 cực trị

Câu 14:

Cho đường cong $(C) : y = \frac{2 x + 3}{x - 1}$ và M là một điểm nằm trên (C). Giả sử $d_{1}, d_{2}$ tương ứng là các khoảng cách từ M đến hai tiệm cận của (C), khi đó $d_{1} . d_{2}$ bằng:

A. 3

B. 4

C. 5

D. 6

Xem đáp án

Đáp án C

Ta có: $\lim_{x \to 1^{+}} y = + \infty \Rightarrow x = 1$ là tiệm cận đứng; $\lim_{x \to + \infty} y = 2 \Rightarrow y = 2$ là tiệm cận ngang

Câu 15:

Hai điểm M, N lần lượt thuộc hai nhánh của đồ thị hàm số $y = \frac{3 x - 1}{x - 3}$ . Khi đó độ dài đoạn thẳng MN ngắn nhất bằng:

A. 8 $\sqrt{2}$

B. 2017

C. 8

D. 4

Xem đáp án

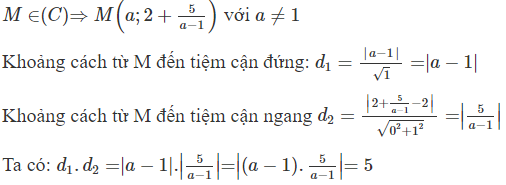
Câu 16:

Cho hàm số $y = \frac{a x^{2} + x - 1}{4 x^{2} + b x + 9}$ có đồ thị (C), trong đó a, b là các hằng số dương thỏa mãn . Biết rằng (C) có đường tiệm cận ngang y = c và có đúng 1 đường tiệm cận đứng. Tính tổng $T = 3 a + b - 24 c$

A. T = 11

B. T = 4

C. T = 7

D. T = -11

Xem đáp án

Đồ thị (C) có đúng 1 đường tiệm cận đứng nên $4 x^{2} + b x + 9 = 0$ có nghiệm kép

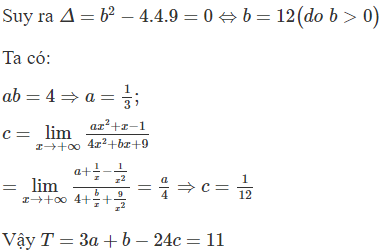
Câu 17:

Cho hàm số f (x) có đạo hàm trên R và có đồ thị của hàm y = f'(x) như hình vẽ. Biết rằng $f (0) + f (3) = f (2) + f (5)$ . Giá trị nhỏ nhất và giá trị lớn nhất của f(x) trên đoạn $[0; 5]$ lần lượt là:

A. f(0), f(5)

B. f(2), f(0)

C. f(1), f(3)

D. f(2), f(5)

Xem đáp án

Đáp án D

Dựa vào đồ thị của hàm số y = f'(x) ta có BBT của hàm số = f(x)

Quan sát BBT ta thấy:

$f (2) < f (3) < f (5)$ và $f (0) > f (2)$

Mặt khác:

$f (0) + f (3) = f (2) + f (5) \Leftrightarrow f (3) - f (2) = f (5) - f (0) > 0 \Rightarrow f (5) > f (0)$

Vậy trên đoạn $[0; 5]$ hàm số $y = f (x)$ có $f (2) < f (0) < f (5)$

Do đó:

+ GTNN của hàm số trên đoạn $[0; 5]$ là f(2)

+ GTLN của hàm số trên đoạn $[0; 5]$ là f(5)

Câu 18:

Cho hàm số f(x) xác định trên R và có đồ thị f'(x) như hình vẽ. Đặt $g (x) = f (x) - x$ . Hàm số g(x) đạt cực đại tại điểm nào sau đây?

A. x = 2

B. x = 0

C. x = -1

D. x = 1

Xem đáp án

Đáp án C

Ta có: $g' (x) = f' (x) - 1$ . Do đó đồ thị hàm số g'(x) có được bằng cách tịnh tiến đồ thị của hàm số f'(x) đi xuống 1 đơn vị

Quan sát đồ thị hàm số g'(x) ta thấy g'(x) đổi dấu từ dương sang âm khi đi qua điểm x = - 1

Do đó g(x) đạt cực đại tại x = - 1

Câu 19:

Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2.000.000 đồng một tháng thì mọi căn hộ đều có người thuê. Mỗi căn hộ không thuê nữa (bỏ trống) thì công ty lại phải tăng số tiền thuê của những căn hộ còn lại thêm 50.000 đồng. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao nhiêu?

A. 115.250.000 đồng

B. 101.250.000 đồng

C. 100.000.000 đồng

D. 100.250.000 đồng

Xem đáp án

Đáp án B

Ở tháng thu nhập của công ty cao nhất, gọi số căn hộ bị bỏ trống là x thì số tiền thuê mỗi phòng là: $2.000.000 + 50.000 x$

Khi đó số tiền thu được là:

$f (x) = (2.000.000 + 50.000 x) - 50.000 x^{2} + 500.000 x + 100.000.000$

Ta cần tìm $x \in (0; 50)$ để f(x) lớn nhất

Ta có: $f' (x) = - 100.000 x + 500.000; f' (x) = 0 \Leftrightarrow x = 5$

Bảng biến thiên:

Vậy mỗi tháng lợi nhuận cao nhất thu được của công ty là 101.250.000

Câu 20:

Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y = x^{4} - 2 m x^{2} + m - 1$ có 3 điểm cực trị. Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1.

A. $[_{m = \frac{- 1 + \sqrt{5}}{2}}^{m = 1}$

B. m = 1

C. $[_{m = \pm \frac{- 1 + \sqrt{5}}{2}}^{m = 1}$

D. $m = \pm \frac{- 1 + \sqrt{5}}{2}$

Xem đáp án

Câu 21:

Tìm giá trị nhỏ nhất của hàm số $y = |\sin x + \cos x + \tan x + c o t x + \frac{1}{\sin x} + \frac{1}{\cos x}|$

A. $2 \sqrt{2} - 1$

B. $\sqrt{2} + 1$

C. $2 \sqrt{2} + 1$

D. $\sqrt{2} - 1$

Xem đáp án

Câu 22:

Biết rằng đồ thị hàm số bậc 4: y = f(x) được cho như hình vẽ sau:

Tìm số giao điểm của đồ thị hàm số $y = g (x) = {[f' (x)]}^{2} - f (x) . f'' (x)$ và trục Ox

A. 0

B. 2

C. 4

D. 6

Xem đáp án

Đáp án A

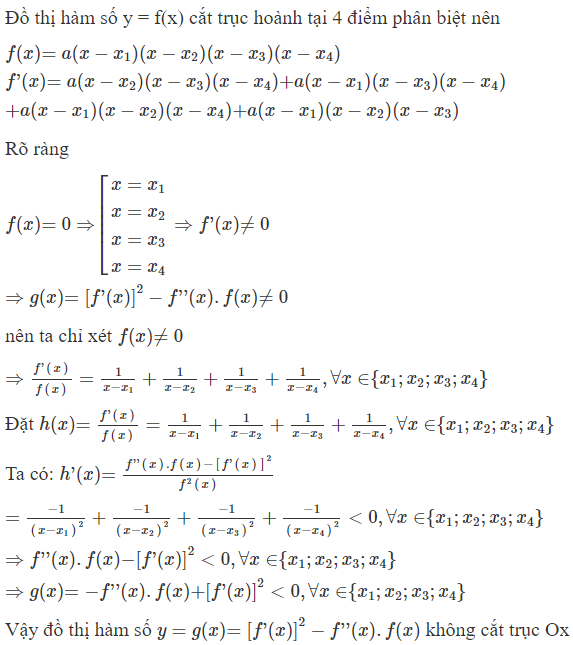
Câu 23:

Với điều kiện $\{\begin{cases} a c (b^{2} - 4 a c) > 0 \\ a b < 0 \end{cases}$ thì đồ thị hàm số $y = a x^{4} + b x^{2} + c$ cắt trục hoành tại bao nhiêu điểm?

A. 4

B. 3

C. 1

D. 2

Xem đáp án

Đáp án A

Số nghiệm của phương trình là số giao điểm của đồ thị hàm số $y = a x^{4} + b x^{2} + c$ với đường thẳng y = 0.

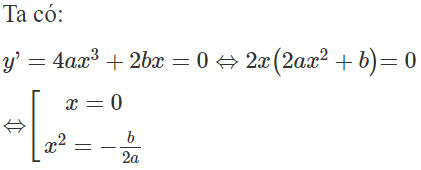
Ta có: $a b < 0 \Rightarrow a, b$ trái dấu $\Rightarrow - \frac{b}{2 a} > 0 \Rightarrow$ phương trình y’ = 0 có 3 nghiệm phân biệt hay đồ thị hàm số có 3 điểm cực trị.

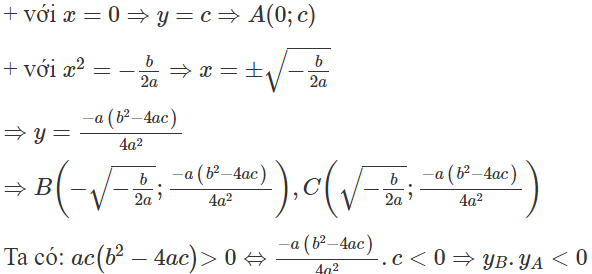
$\Rightarrow$ các điểm cực đại và cực tiểu nằm khác phía so với trục hoành.

$\Rightarrow$ đồ thị hàm số $y = a x^{4} + b x^{2} + c$ cắt trục hoành tại 4 điểm phân biệt.

Câu 24:

Cho hàm số $f (x) = x^{3} + a x^{2} + b x - 2$ thỏa mãn $\{\begin{cases} a + b > 1 \\ 3 + 2 a + b < 0 \end{cases}$ . Số điểm cực trị của hàm số $y = |f (|x|)|$ bằng:

A. 5

B. 9

C. 2

D. 11

Xem đáp án

Đáp án D

Ta có: $f (x) = x^{3} + a x^{2} + b x - 2$

$+ f (0) = - 2 < 0; f (1) = a + b - 1 > 0 \Rightarrow f (0) . f (1) < 0$

$\Rightarrow$ phương trình f(x) = 0 có ít nhất 1 nghiệm $x_{1} \in (0; 1)$

$+ f (2) = 2 (3 + 2 a + b) < 0 \Rightarrow f (2) . f (1) < 0$

$\Rightarrow$ phương trình f(x) = 0 có ít nhất 1 nghiệm $x_{2} \in (1; 2)$

Do đó phương trình f(x) = 0 có ít nhất 2 nghiệm và đồ thị hàm số y = f(x) chỉ có thể có dạng:

Khi đó, đồ thị hàm số $y = f (|x|)$ (màu tím) và $y = |f (|x|)|$ (màu cam) lần lượt có đồ thị như sau:

Như vậy, hàm số $y = |f (|x|)|$

Câu 25:

Cho hàm số y = f(x) có đồ thị hàm số f'(x) như hình vẽ. Hàm số $y = f (1 - x) + \frac{x^{2}}{2} - x$ nghịch biến trên khoảng

A. (-3; 1)

B. (-2; 0)

C. (1; 3)

D. (−1; 3/2)

Xem đáp án

Đáp án B

$y = f (1 - x) + \frac{x^{2}}{2} - x \Rightarrow y' = - f' (1 - x) + x - 1 y' = 0 \Leftrightarrow f' (1 - x) > - (1 - x)$

Dựa vào đồ thị hàm số, ta có: Đồ thị hàm số f'(x) cắt đường thẳng y = -x tại 3 điểm phân biệt là: $A (- 3; 3), B (- 1; 1), C (3; - 3)$

$A (- 3; 3), B (- 1; 1), C (3; - 3)$

Hàm số $y = f (1 - x) + \frac{x^{2}}{2} - x$ nghịch biến trên các khoảng $(- 2; 0), (4; + \infty)$

Câu 26:

Có bao nhiêu giá trị nguyên của tham số m để hàm số $y = x^{8} + (m - 2) x^{5} - (m^{2} - 4) x^{4} + 1$ đạt cực tiểu tại x = 0?

A. 3

B. 5

C. 4

D. Vô số

Xem đáp án

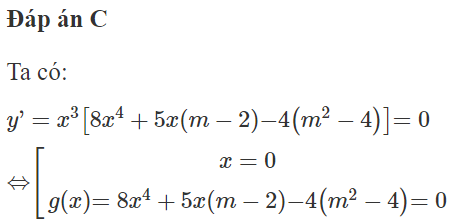
Do x = 0 là một nghiệm của đạo hàm nên hàm số đạt cực tiểu tại x = 0 $\Leftrightarrow y'$ đổi dấu từ - sang + khi qua nghiệm x = 0.

+ TH1: x = 0 là nghiệm của g(x) hay $m = \pm 2$

Với m = 2 thì g(x) = 0 có nghiệm x = 0 bội 4 theo kết quả ở trên thì x = 0 là nghiệm bội 7 của y’ nên x = 0 là điểm cực tiểu của hàm số nên chọn m = 2.

Với m = - 2 thì g(x) có nghiệm x = 0 và 1 nghiệm dương, lúc này x = 0 là nghiệm bội 4 của f'(x) nên x = 0 không là điểm cực trị của hàm số. Loại m = - 2.

+ TH2: x = 0 không là nghiệm của g(x) hay $m \neq \pm 2$ . Ta có: $g (0) = - 4 (m^{2} - 4)$

$y' = x^{3} g (x)$ đổi dấu từ - sang + qua nghiệm x = 0 khi và chỉ khi

$\Leftrightarrow - 4 (m^{2} - 4) > 0 \Leftrightarrow m^{2} - 4 < 0 \Leftrightarrow - 2 < m < 2$

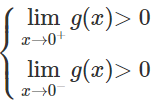
Do m nguyên nên $m \in \{- 1; 0; 1\}$

Kết hợp hai trường hợp ta được $m \in \{- 1; 0; 1; 2\}$

Câu 27:

Cho hàm số $y = \frac{x - 2}{x + 1}$ có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của (C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng:

A. $2 \sqrt{3}$

B. $2 \sqrt{2}$

C. $\sqrt{3}$

D. $\sqrt{6}$

Xem đáp án

Đáp án A

Ta có x = - 1 là TCĐ của đồ thị hàm số, y = 1 là TCN của đồ thị hàm số.

$\Rightarrow I (- 1; 1)$ là giao điểm của hai đường tiệm cận của dồ thị hàm số

Dựa vào đồ thị hàm số ta có $Δ I A B$ là tam giác đều.

$\Rightarrow I H$ vừa là đường cao đồng thời là đường phân giác của $\hat{A I B} \Rightarrow I H$ cũng là đường phân giác của góc phần tư thứ hai.

$\Rightarrow I H : y = - x$

Ta có: $A B ⊥ I H \Rightarrow A B : y = x + m \Leftrightarrow x - y + m = 0$

$\Rightarrow d (I; A B) = \frac{|- 1 - 1 + m|}{\sqrt{2}} = \frac{|m - 2|}{\sqrt{2}}$

Xét phương trình hoành độ giao điểm $\frac{x - 2}{x + 1} = x + m \Leftrightarrow x^{2} + m x + m + 2 = 0$

Phương trình có 2 nghiệm phân biệt $\Leftrightarrow m^{2} - 4 (m + 2) > 0 \Leftrightarrow m^{2} - 4 m > 8$

Khi đó hoành độ các giao điểm A, B là nghiệm của phương trình trên

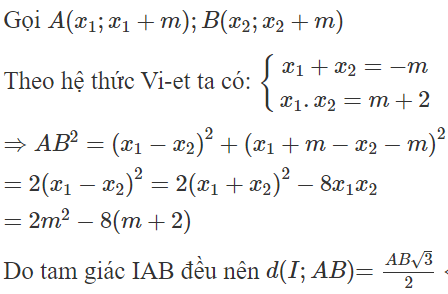
⇔d2(I;

Câu 28:

Cho hàm số $y = \frac{1}{6} x^{4} - \frac{7}{3} x^{2}$ có đồ thị hàm số (C). Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt $M (x_{1}; y_{1}), N (x_{2}; y_{2}) (M, N \neq A)$ thỏa mãn $y_{1} - y_{2} = 4 (x_{1} - x_{2})$ ?

A. 3

B. 0

C. 1

D. 2

Xem đáp án

Đáp án D

Gọi $A (x_{0}; y_{0}) \in (C)$

Khi đó tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt $M (x_{1}; y_{1}), N (x_{2}; y_{2}) (M, N \neq A)$ có hệ số góc là $k = \frac{y_{1} - y_{2}}{x_{1} - x_{2}} = 4$

$k = \frac{y_{1} - y_{2}}{x_{1} - x_{2}} = 4$

$k = \frac{y_{1} - y_{2}}{x_{1} - x_{2}} = 4$ iểm tra lại từng trường hợp $x_{0} = - 2; - 1; 3$ ta thấy trường hợp $x_{0} = 3$ thì tiếp tuyến chỉ có duy nhất 1 điểm chung với đồ thị nên loại

Vậy có 2 giá trị của m thỏa mãn.

Câu 29:

Cho hàm số $y = f (x), y = g (x)$ . Hai hàm số $y = f' (x), y = g' (x)$ có đồ thị hàm số như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số $y = g' (x)$ .

Hàm số $h (x) = f (x + 6) - g (2 x + \frac{5}{2})$ đồng biến trên khoảng nào dưới đây?

A. (21/5; + $\infty$ )

B. (1/4; 1)

C. (3; 21/5)

D. (4; 17/4)

Xem đáp án

Đáp án B

Dựa vào đồ thị hàm số ta thấy đường thẳng y = 10 cắt đồ thị hàm số y = f'(x) tại hai điểm phân biệt $(3; 10); (m; 10)$ với mọi $m \in (8; 10)$

Ta có:

$f' (x + 6) \geq 10 \Leftrightarrow 3 \leq x + 6 \leq m < 10 \Rightarrow - 3 \leq x < 4 g' (2 x + \frac{5}{2}) \leq 5, \forall x \in R \Rightarrow h' (x) = f' (x + 6) - 2 g' (2 x + \frac{5}{2}) \geq 10 - 2.5 = 0, \forall x \in [- 3; 4]$

Do đó hàm số h(x) đồng biến trên $[- 3; 4]$

Dựa vào các đáp án ta thấy đáp án B thỏa mãn

Câu 30:

Cho hàm số $f (x) = x^{3} - 6 x^{2} + 9 x$ . Đặt $f^{k} (x) = f (f^{k - 1} (x))$ (với k là số tự nhiên lớn hơn 1). Tính số nghiệm của phương trình $f^{8} (x) = 0$

A. 3281

B. 3280

C. 6561

D. 6562

Xem đáp án

Đáp án A

Ta có đồ thị hàm số $f (x) = x^{3} - 6 x^{2} + 9 x$ như sau:

Dựa vào đồ thị hàm số ta có thể suy ra số nghiệm của phương trình f(x) = m như sau:

$[\begin{matrix} m < 0 \\ m > 4 \end{matrix} \Rightarrow$ phương trình có 1 nghiệm duy nhất

$[\begin{matrix} m = 0 \\ m = 4 \end{matrix} \Rightarrow$ phương trình có 2 nghiệm phân biệt

$0 < m < 4 \Rightarrow$ phương trình có 3 nghiệm phân biệt

Xét phương trình

$f^{2} (x) = 0 \Leftrightarrow {(f (x))}^{3} - 6 {(f (x))}^{2} + 9 f (x) = 0 \Leftrightarrow [\begin{matrix} f (x) = 0 \\ f (x) = 3 \end{matrix}$

Ta thấy phương trình f(x) = 0 có 2 nghiệm phân biệt, phương trình f(x) = 3 có 3 nghiệm phân biệt

Vậy phương trình $f^{2} (x) = 0$ có 5 nghiệm phân biệt

Xét phương trình

Ta thấy mỗi phương trình $f^{2} (x) = m$ ở trên có 9 nghiệm phân biệt nên 3 phương trình sẽ có $3.9 = 3^{3}$ nghiệm phân biệt.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án

Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án (P2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương