16 câu hỏi trắc nghiệm thuộc Trắc nghiệm Sự đồng biến , nghịch biến của hàm số có đáp án năm 2021 -2022

Câu 1:

Cho hàm số $y = \frac{x + 1}{1 - x}$ . Khẳng định nào sao đây là khẳng đinh đúng?

A. Hàm số nghịch biến trên khoảng $(- \infty; 1) \cup (1; + \infty)$ .

B. Hàm số đồng biến trên khoảng $(- \infty; 1) \cup (1; + \infty)$ .

C. Hàm số nghịch biến trên các khoảng $(- \infty; 1)$ và $(1; + \infty)$ .

D. Hàm số đồng biến trên các khoảng $(- \infty; 1)$ và $(1; + \infty)$ .

Xem đáp án

TXĐ: $D = ℝ \ \{1\}$ . Ta có $y' = \frac{2}{{(1 - x)}^{2}} > 0, \forall x \neq 1$

Hàm số đồng biến trên các khoảng $(- \infty; 1)$ và $(1; + \infty)$ .

Chọn D.

Câu 2:

Cho hàm số $y = \frac{3 x - 1}{- 4 + 2 x}$ . Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn nghịch biến trên $ℝ$ .

B. Hàm số luôn nghịch biến trên từng khoảng xác định.

C. Hàm số đồng biến trên các khoảng $(- \infty; 2)$ và $(2; + \infty)$ .

D. Hàm số nghịch biến trên các khoảng $(- \infty; - 2)$ và $(- 2; + \infty)$ .

Xem đáp án

TXĐ: $D = ℝ \ \{2\}$ . Ta có $y' = - \frac{10}{{(- 4 + 2 x)}^{2}} < 0, \forall x \in D$ .

Chọn B.

Câu 3:

Cho hàm số $y = - x^{3} + 3 x^{2} - 3 x + 2$ . Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn nghịch biến trên $ℝ$ .

B. Hàm số nghịch biến trên các khoảng $(- \infty; 1)$ và $(1; + \infty)$ .

C. Hàm số đồng biến trên khoảng $(- \infty; 1)$ và nghịch biến trên khoảng $(1; + \infty)$ .

D. Hàm số luôn đồng biến trên $ℝ$ .

Xem đáp án

TXĐ: $D = ℝ$ . Ta có

$y' = - 3 x^{2} + 6 x - 3 = - 3 {(x - 1)}^{2} \leq 0, \forall x \in ℝ$

Do đó hàm số đã cho luôn nghịch biến trên $ℝ$ .

Chọn A.

Câu 4:

Hàm số $y = \sqrt{x - x^{2}}$ nghịch biến trên khoảng nào dưới đây?

A. $(\frac{1}{2}; 1) .$

B. $(0; \frac{1}{2}) .$

C. $(- \infty; 0) .$

D. $(1; + \infty) .$

Xem đáp án

$y^{'} = \frac{1 - 2 x}{2 \sqrt{x - x^{2}}} < 0 \Leftrightarrow \{\begin{cases} x - x^{2} > 0 \\ 1 - 2 x > 0 \end{cases}$ $\Leftrightarrow \{\begin{cases} 0 < x < 1 \\ x < \frac{1}{2} \end{cases} \Leftrightarrow 0 < x < \frac{1}{2}$

Chọn B.

Câu 5:

Hàm số $y = \frac{x^{2} - 2 x}{x - 1}$ đồng biến trên khoảng

A. (- $\infty$ ; 1) $\cup$ (1; + $\infty$ ).

B. (- $\infty$ ; 1) và (1; + $\infty$ ).

C. R\{1}.

D. (- $\infty$ ; + $\infty$ ).

Xem đáp án

Ta có: $y = \frac{{(x - 1)}^{2} - 1}{x - 1} = x - 1 - \frac{1}{x - 1}$ $\Rightarrow y^{'} = 1 + \frac{1}{{(x - 1)}^{2}} > 0, \forall x \neq 1$ .

Chọn B.

Câu 6:

Hàm số $y = \frac{x^{2} + x - 3}{x + 1}$ đồng biến trên các khoảng (các khoảng) nào sau đây?

A. (-2; 1).

B. (- $\infty$ ; + $\infty$ ).

C. (- $\infty$ ; -1) và (-1; + $\infty$ ).

D. (- $\infty$ ; + $\infty$ )\{-1}.

Xem đáp án

Ta có: $y = x - \frac{3}{x + 1}$ $\Rightarrow y^{'} = 1 + \frac{3}{{(x + 1)}^{2}} > 0, \forall x \neq - 1$ .

Chọn C.

Câu 7:

Trên các khoảng nghịch biến của hàm số $y = \frac{x^{2} - 3 x - 1}{2 + x}$ có chứa bao nhiêu số nguyên âm?

A. 1.

B. 4.

C. 2.

D. 3.

Xem đáp án

$y^{'} = \frac{(2 x - 3) (2 + x) - (x^{2} - 3 x - 1)}{{(2 + x)}^{2}}$ $= \frac{x^{2} + 4 x - 5}{{(2 + x)}^{2}} < 0$ $\Leftrightarrow \{\begin{cases} x \neq - 2 \\ x^{2} + 4 x - 5 < 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} x \neq - 2 \\ - 5 < x < 1 \end{cases}$ $\Rightarrow x \in \{- 4; - 3; - 1\}$

Chọn D.

Câu 8:

Cho hàm số $y = x^{3} - 3 x^{2} + 2$ . Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số nghịch biến trên khoảng (- $\infty$ ; 0) và (6; + $\infty$ ).

B. Hàm số nghịch biến trên khoảng (0; 6).

C. Hàm số nghịch biến trên khoảng (0; 2).

D. Hàm số nghịch biến trên khoảng (- $\infty$ ; 0) và (2; + $\infty$ ).

Xem đáp án

Ta có: $y^{'} = 3 x^{2} - 6 x < 0 \Leftrightarrow 0 < x < 2$ .

Chọn C.

Câu 9:

Cho hàm số có bảng biến thiên như sau:

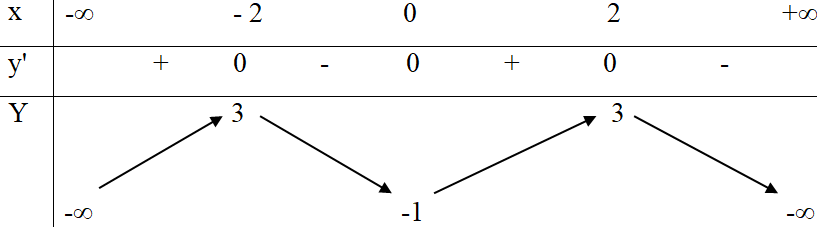
Hàm số nghịch biến trên khoảng nào dưới đây?

A. (-2; 0).

B. (- $\infty$ ; -2).

C. (0; 2).

D. (0; + $\infty$ ).

Xem đáp án

Dựa vào bảng biến thiên, ta có:

Hàm số nghịch biến trên $(- 2; 0) \cup (2; + \infty) .$

Chọn A.

Câu 10:

Cho hàm số $y = f (x) = 5 x^{4} - 10 x^{2} + 3$ .

Hàm số đã cho nghịch biến trên khoảng nào sau đây?

A. (0; 1).

B. (- $\infty$ ; 0).

C. (1; + $\infty$ ).

D. (-1; 0).

Xem đáp án

TXĐ: $D = ℝ$ .

$y' = 20 x^{3} - 20 x;$ $y' = 0 \Leftrightarrow 20 x^{3} - 20 x = 0$ $\Leftrightarrow 20 x (x^{2} - 1) = 0$

$\Leftrightarrow [\begin{array}{l} 20 x = 0 \\ x^{2} - 1 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = 1 \\ x = - 1 \end{array}$

Ta có bảng biến thiên:

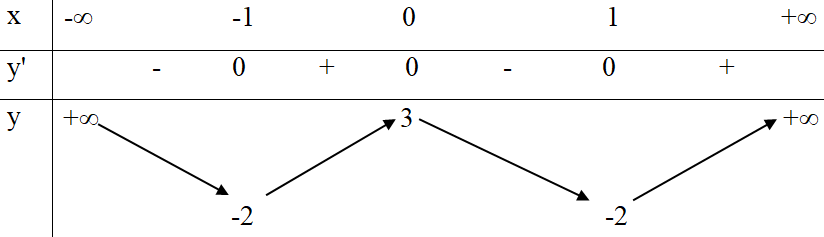
Vậy hàm số nghịch biến trên $(- \infty; - 1) \cup (0; 1) .$

Chọn A.

Câu 11:

Cho hàm số $y = f (x)$ có bảng biến thiên như sau:

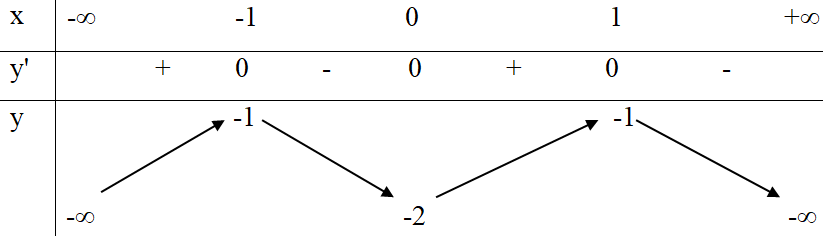
Hàm số đã cho đồng biến trên khoảng nào sau đây?

A. (-1; 0).

B. (1; + $\infty$ ).

C. (- $\infty$ ; 1).

D. (0; 1).

Xem đáp án

Dựa vào bảng biến thiên, ta có: Hàm số $f (x)$ đồng biến trên khoảng $(- \infty; - 1)$ và $(0; 1)$ .

Chọn D.

Câu 12:

Hàm số $y = f (x)$ liên tục trên $ℝ \ \{1; 0\}$

và có bảng biến thiên như sau:

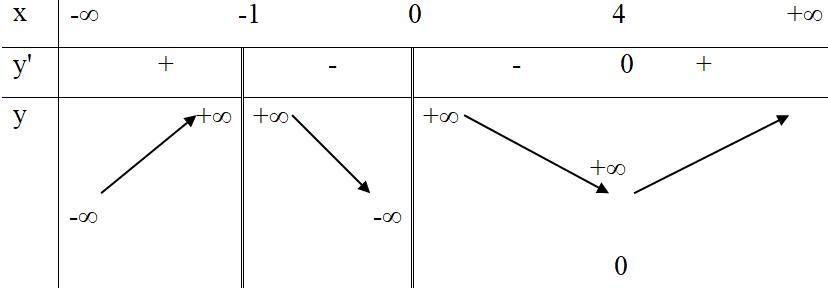
Hỏi hàm số đồng biến trên khoảng

(các khoảng) nào dưới đây?

A. (- $\infty$ ; -1) $\cup$ (0; + $\infty$ ).

B. (- $\infty$ ; -1) , (4; + $\infty$ ).

C. (- $\infty$ ; + $\infty$ ).

D. (- $\infty$ ; + $\infty$ )\{-1;0}.

Xem đáp án

Dựa vào bảng biến thiên, ta có: Hàm số $f (x)$ đồng biến trên khoảng $(- \infty; - 1)$ và $(4; + \infty)$ .

Chọn B.

Câu 13:

Hàm số $y = f (x)$ xác định trên $ℝ \ \{1\}$

và có bảng biến thiên như sau:

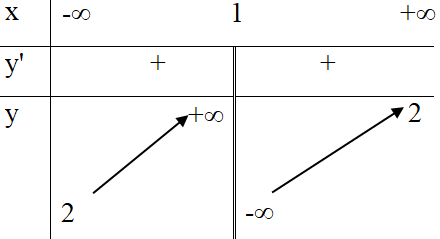
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số đồng biến trên khoảng (- $\infty$ ; 1) $\cup$ (1; + $\infty$ ).

B. Hàm số đồng biến trên khoảng (- $\infty$ ; 2) $\cup$ (2; + $\infty$ ).

C. Hàm số đồng biến trên khoảng (- $\infty$ ; -1) và (1; + $\infty$ ).

D. Hàm số đồng biến trên $ℝ \ \{1\}$ .

Xem đáp án

Dựa vào bảng biến thiên, ta có: Hàm số đồng biến trên khoảng $(- \infty; - 1)$ và $(1; + \infty)$ .

Chọn C.

(Ngoài ra còn có cách kết luận khác là hàm số đồng biến trên từng khoảng xác định của nó).

Câu 14:

Hàm số $y = f (x)$ có bảng biến thiên

như hình vẽ sau:

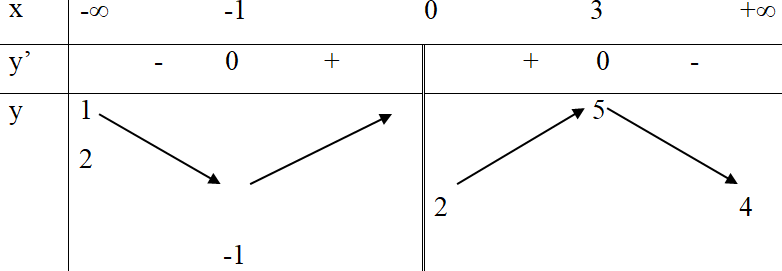
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số đồng biến trên các khoảng (-2; 1), (1; 3).

B. Hàm số đồng biến trên các khoảng (-1; 2), (2; 5).

C. Hàm số nghịch biến trên các khoảng (-1; 1), (4; 5).

D. Hàm số nghịch biến trên các khoảng (- $\infty$ ; -1), (3; + $\infty$ ).

Xem đáp án

Dựa vào bảng biến thiên, ta có: Hàm số nghịch biến trên các khoảng $(- \infty; - 1)$ , $(3; + \infty)$ .

Chọn D.

Câu 15:

Hàm số $y = f (x)$ có bảng biến thiên như sau:

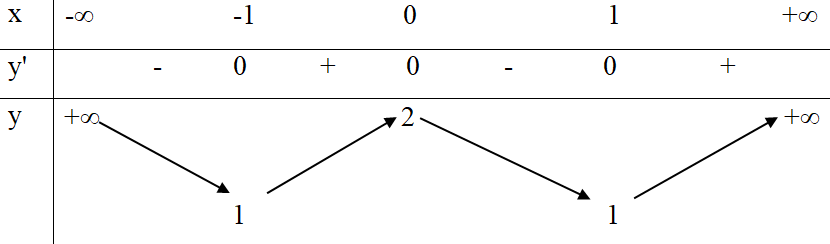
Khẳng định nào sau đây là khẳng định sai?

A. $f (x) \geq 1, \forall x \in R .$

B. $f (\frac{1}{2}) < f (0) .$

C. $f (1) > f (0) .$

D. $f (- 1) < f (- 2) .$

Xem đáp án

Dựa vào bảng biến thiên, ta thấy: Hàm số nghịch biến trên (0; 1) nên $f (1) < f (0)$ .

Do đó đáp án C sai.

Chọn C.

Câu 16:

Hàm số $y = f (x)$ có bảng biến thiên như sau:

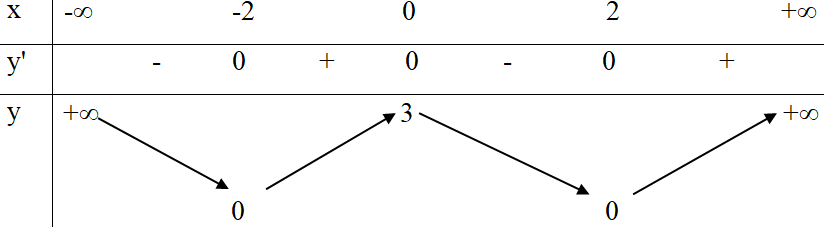
Khẳng định nào sau đây là khẳng định sai?

A. Hàm số nghịch biến trên (- $\infty$ ; -2) và (0; 2).

B. Hàm số đồng biến trên (-2; 0) và (2; + $\infty$ ).

C. $f (x) \geq 0, \forall x \in ℝ .$

D. Hàm số đồng biến trên (0; 3) và (0; + $\infty$ ).

Xem đáp án

Dựa vào bảng biến thiên, ta thấy:

Hàm số nghịch biến trên (- $\infty$ ; -2) và (0; 2). Do đó A đúng.

Hàm số đồng biến trên (-2; 0) và (2; + $\infty$ ). Do đó B đúng.

Ta thấy các giá trị của $f (x) \geq 0, \forall x \in ℝ .$ Do đó C đúng.

Hàm số không đồng biến trên (0; 3) và (0; + $\infty$ ). Do đó D sai.

Chọn D.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Sự đồng biến , nghịch biến của hàm số có đáp án năm 2021 -2022

Trắc nghiệm Sự đồng biến , nghịch biến của hàm số có đáp án năm 2021 -2022

Danh sách câu hỏi