Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 69)
-
855 lượt thi
-
87 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Hùng và Dũng có tất cả 45 viên bi. Nếu Hùng có thêm 5 viên bi thì Hùng có nhiều hơn Dũng 14 viên bi. Tìm số bi của mỗi bạn?
 Xem đáp án
Xem đáp án
Hùng hơn Dũng số viên bi là:
14 – 6 = 9 (viên bi)
Số bi của Hùng là :
(45 + 9) : 2 = 27 (viên bi)
Số bi của Dũng là:
27 – 9 = 18 (viên bi)
Đáp số: 18 viên bi, 27 viên bi
Câu 2:
Hai thùng dầu có tổng cộng 82 lít dầu. Nếu rót 7 lít dầu từ thùng thứ nhất sang thùng thứ hai thì hai thùng chứa lượng dầu bằng nhau. Hỏi mỗi thùng chứa bao nhiêu lít dầu?
 Xem đáp án
Xem đáp án
Thùng thứ nhất hơn thùng thứ hai số lít dầu là:
7 × 2 = 14 (l)
Thùng thứ nhất có số lít dầu là:
(82 + 14) : 2 = 48 (l)
Thùng thứ hai có số lít dầu là:
82 – 48 = 34 (l)
Đáp số: 48 lít; 34 lít
Câu 3:
Biết đa thức f(x) = x3 + ax2 + bx + 2 chia cho x + 1 dư 5, chia cho x + 2 dư 8. Khi đó giá trị của a và b là bao nhiêu?
 Xem đáp án
Xem đáp án
Ta có: f(x) = x3 + ax2 + bx + 2 chia cho x + 1 dư 5
Suy ra f(x) – 5 chia hết cho x + 1
Hay x3 + ax2 + bx + 2 – 5 chia hết cho x + 1
Suy ra x3 + ax2 + bx – 3 chia hết cho x + 1
Do đó x = -1 là nghiệm của đa thức f(x)
Khi đó (-1)3 + a(-1)2 + b(-1) - 3 = 0
Þ -1 + a – b – 3 = 0
Þ a – b = 4 hay b = a – 4
Tương tự ta được f(x) – 8 chia hết cho x + 2
Hay x3 + ax2 + bx + 2 – 8 chia hết cho x + 2
Suy ra x3 + ax2 + bx – 6 chia hết cho x + 2
Þ x = –2 là nghiệm của đa thức f(x)
Þ (–2)3 + a(–2)2 + b(–2) – 6 = 0
Þ –8 + 4a – 2b – 6 = 0
Þ 4a – 2b = 14
Þ 2a – b = 7
Thay b = a – 4 vào ta có:
2a – (a – 4) = 7
2a – a + 4 = 7
a + 4 = 7
a = 3
Þ b = 3 – 4 = –1
Vậy (a; b) = (3; –1)
Câu 4:
Biết đa thức f(x) = x3 + ax + b chia cho x – 2 dư 3, chia cho x – 3 dư 5. Tìm đa thức đó.
 Xem đáp án
Xem đáp án
Ta có: (x) = x3 + ax + b chia cho x – 2 dư 3
Suy ra f(x) – 3 chia hết cho x – 2
Hay x3 + ax + b – 3 chia hết cho x – 2
Do đó x = 2 là nghiệm của đa thức f(x)
Khi đó 23 + 2a + b – 3 = 0
Þ 8 + 2a + b – 3 = 0
Þ 2a + b = –5 hay b = –2a – 5
Tương tự ta được f(x) – 5 chia hết cho x – 3
Hay x3 + ax + b – 5 chia hết cho x – 3
Do đó x = 3 là nghiệm của đa thức f(x)
Þ 33 + 3a + b – 5 = 0
Þ 27 +3a + b – 5 = 0
Þ 3a + b = –22
Thay b = –2a – 5 vào ta có:
3a + (–2a – 5) = –22
3a – 2a – 5 = –22
a – 5 = –22
a = –17
Þ b = (–2)(–17) – 5 = 29
Vậy đa thức f(x) = x3 – 22 + 29.
Câu 5:
Tìm hai bội của 49.
 Xem đáp án
Xem đáp án
Ta có: 49. 1 = 49
49. 2 = 98
Suy ra 49 và 98 là hai bội của 49
Vậy 2 bội của 49 là 49 và 98.
Câu 6:
Tìm các ước của 108.
 Xem đáp án
Xem đáp án
Ta có: 108 = 22. 33
Þ Ư(108) = {1; 2; 3; 4; 9; 27; 108}
Vậy các ước của 108 là {1; 2; 3; 4; 9; 27; 108}
Câu 7:
Một hình vuông có chu vi là 20 m. Tính diện tích hình vuông đó.
 Xem đáp án
Xem đáp án
Cạnh hình vuông là :
20 : 4 = 5 (m )
Diện tích hình vuông là :
5 × 5 = 25 (m2)
Đáp số: 25 m2
Câu 8:
Một hình vuông có diện tích là 36 m2. Tính chu vi hình vuông đó.
 Xem đáp án
Xem đáp án
36 = 6 × 6
Cạnh hình vuông là: 6 m
Chu vi hình vuông là:
6 × 4 = 24 (m)
Đáp số: 24 m
Câu 9:
Chứng minh rằng: A = a3 – a chia hết cho 3.
 Xem đáp án
Xem đáp án
Ta có: A = a3 – a = a(a2 – 1) = a(a – 1)(a + 1)
Vì a(a – 1)(a + 1) là tích của 3 số nguyên liên tiếp nên a(a – 1)(a + 1) chia hết cho 3
Vậy A chia hết cho 3.
Câu 10:
Có bao nhiêu số từ 1 đến 100 là bội của 5 và chia hết cho 3.
 Xem đáp án
Xem đáp án
Nếu số đó là bội của 5 và chia hết cho 3 thì số đó là bội của 15.
Các số từ 1 đến 100 là B(15) là: 15; 30; 45; 60; 75; 90
Vậy có 6 số từ 1 đến 100 là bội của 5 và chia hết cho 3.
Câu 11:
Có bao nhiêu số từ 1 đến 300 là bội của 7 và chia hết cho 3 và 5.
 Xem đáp án
Xem đáp án
Nếu số đó là bội của 7 và chia hết cho 3 và 5 thì số đó là bội của 105.
Các số từ 1 đến 300 là B(105) là: 105; 210
Vậy có 2 số từ 1 đến 300 là bội của 7 và chia hết cho 3 và 5.
Câu 12:
Một sân vận động hình chữ nhật có chiều dài 180 m, chiều rộng bằng nửa chiều dài. Tính diện tích của sân vận động đó.
 Xem đáp án
Xem đáp án
Chiều rộng của sân vận động đó hình chữ nhật là:
180 : 2 = 90 (m)
Diện tích của sân vận động hình chữ nhật là:
180 × 90 = 16 200 (m2)
Đáp số: 16200 m2
Câu 13:
Một sân vận động hình chữ nhật có chu vi là 400 m, chiều dài bằng \[\frac{3}{2}\] chiều rộng. Tính chiều dài và chiều rộng của sân vận động.
 Xem đáp án
Xem đáp án
Nửa chu vi sân vận động hình chữ nhật là:
400 : 2 = 200 (m)
Ta có sơ đồ:
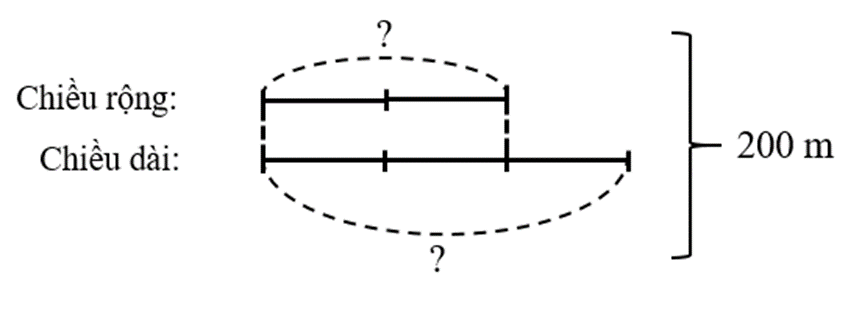
Chiều dài sân vận động hình chữ nhật là:
200 : (2 + 3) × 3 = 120 (m)
Chiều rộng sân vận động hình chữ nhật là:
200 – 120 = 80 (m)
Đáp số: Chiều dài: 120 m;
Chiều rộng: 80 m
Câu 14:
Một ao cá hình vuông có diện tích 0,16 ha. Tính chu vi ao cá đó.
 Xem đáp án
Xem đáp án
Vì ao cá là hình vuông nên cạnh của ao cá là 0,4 hm
Chu vi ao cá là:
0,4 × 4 = 1,6 (hm)
Đáp số: 1,6 hm
Câu 15:
Một hình vuông có chu vi bằng 36cm. Tính diện tích của hình vuông đó.
 Xem đáp án
Xem đáp án
Cạnh của hình vuông là:
36 : 4 = 9 (cm)
Diện tích hình vuông là:
9 × 9 = 36 (m2)
Đáp số: 36 m2
Câu 16:
Một thửa ruộng hình chữ nhật có chu vi 240 m, chiều rộng bằng \[\frac{3}{5}\] chiều dài. Người ta cấy lúa trên thửa ruộng đó cứ 5 m2 thu được \[\frac{8}{5}\] kg thóc. Tính số thóc thu được?
 Xem đáp án
Xem đáp án
Nửa chu thửa ruộng vi hình chữ nhật là:
240 : 2 = 120 (m)
Ta có sơ đồ:
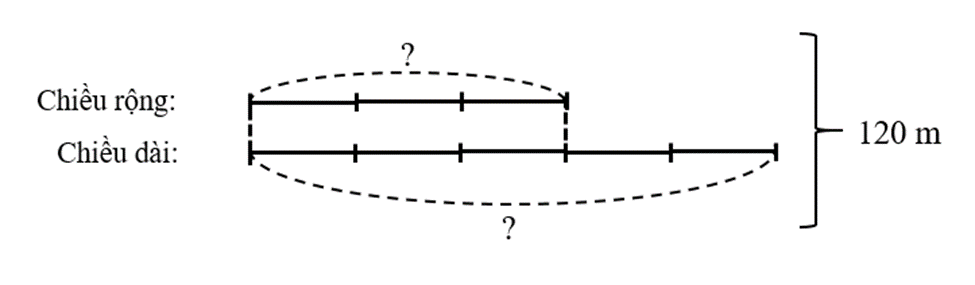
Chiều rộng thửa ruộng hình chữ nhật là:
120 : (3 + 5) × 3 = 45 (m)
Chiều dài thửa ruộng hình chữ nhật là:
120 – 45 = 75 (m)
Diện tích thửa ruộng hình chữ nhật là:
45 × 75 = 3375 (m2)
Một m2 thu được số thóc là:
\[\frac{8}{5}\]: 5 = \[\frac{8}{{25}}\] (kg)
Số thóc thu được là:
3375 × \[\frac{8}{{25}}\] = 1080 (kg)
Đáp số: 1080 kg
Câu 17:
Một đội công nhân sửa đường. Trong tháng 7 sửa được 12,54 km, tháng 8 sửa gấp 2 lần tháng 7 và nhiều hơn tháng 9 là 3,45 km. Hỏi trong quý III đội công nhân đó sửa được bao nhiêu ki-lô-mét đường?
 Xem đáp án
Xem đáp án
Tháng 8 sửa được số ki-lô-mét đường là:
12,54 × 2 = 25,08 (km)
Tháng 8 sửa được số ki-lô-mét đường là:
12,54 – 3,45 = 9,09 (km)
Trong quý III đội công nhân đó sửa được số ki-lô-mét đường là:
12,54 + 25,08 + 9.09 = 46,71 (km)
Đáp số: 46,71 km
Câu 18:
Một đội công nhân sửa đường trong 15 ngày đầu sửa được 475 m đường, 12 ngày sau sửa được 470 m. Hỏi trung bình mỗi ngày đội công nhân đó sửa được bao nhiêu mét đường?
 Xem đáp án
Xem đáp án
Đội đó làm trong số ngày là:
15 + 12 = 27 (ngày)
Trong 27 ngày đội đó sửa được số mét đường là:
475 + 470 = 945 (m)
Trung bình mỗi ngày đội đó sửa được số mét đường là:
945 : 27 = 35 (m)
Đáp số: 35 m
Câu 19:
Một người có 150kg gạo tẻ và gạo nếp. Sau khi người đó bán đi 30kg gạo tẻ thì số gạo nếp bằng \[\frac{3}{5}\] số gạo tẻ còn lại. Hỏi lúc đầu người đó có bao nhiêu kg gạo mỗi loại?
 Xem đáp án
Xem đáp án
Số gạo tẻ và nếp còn lại là:
150 – 30 = 120 (kg)
Ta có sơ đồ:
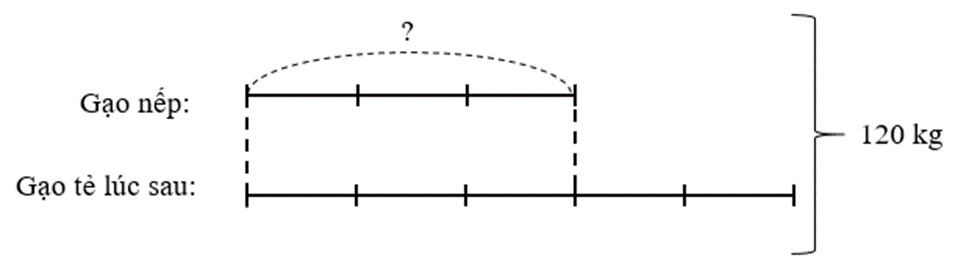
Số gạo nếp là:
120 : (3 + 5) × 3 = 45 (kg)
Số gạo tẻ lúc sau :
120 – 45 = 75 (kg)
Số gạo tẻ lúc đầu :
75 + 30 = 105 (kg)
Đáp số: Gạo tẻ: 105 kg;
Gạo nếp: 45 kg
Câu 20:
Một người có 200kg ngô và khoai. Sau khi người đó bán đi 30 kg ngô và 10 kg khoai thì số ngô còn lại bằng \[\frac{1}{3}\] số khoai còn lại. Hỏi lúc đầu người đó có bao nhiêu kg ngô và khoai?
 Xem đáp án
Xem đáp án
Số ngô và khoai còn lại là:
200 – 30 – 10 = 160 (kg)
Ta có sơ đồ:
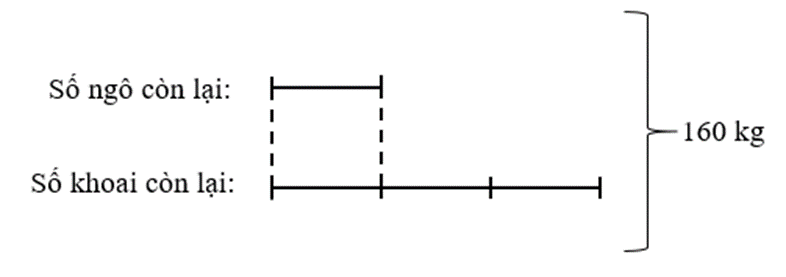
Số ngô còn lại là:
160 : (3 + 1) × 1 = 40 (kg)
Số khoai còn lại là:
160 – 40 = 120 (kg)
Số ngô lúc đầu là:
40 + 30 = 70 (kg)
Số khoai lúc đầu là:
200 – 70 = 130 (kg)
Đáp số: Ngô: 70 kg;
Khoai: 130 kg
Câu 21:
Chứng minh rằng: (x – y)(xn – yn) chia hết cho (x – y)2.
 Xem đáp án
Xem đáp án
Ta có xn – yn = (x – y)(xn-1 + xn-2y + xn-3y2 +…+ xyn-2 + yn-1)
Vì x – y chia hết cho x – y nên (x – y)(xn-1 + xn-2y + xn-3y2 +…+ xyn-2 + yn-1) chia hết cho x – y.
Suy ra (x – y)(x – y)(xn-1 + xn-2y + xn-3y2 +…+ xyn-2 + yn-1) chia hết cho (x – y)2
Vậy (x – y)(xn – yn) chia hết cho (x – y)2.
Câu 22:
Cho tam giác ABC cân tại A có BC = 6cm, đường cao AH = 4 cm. Tính diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
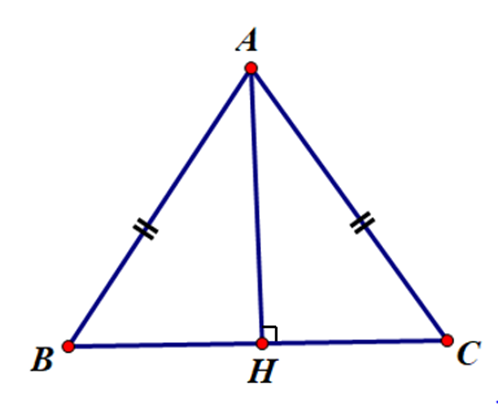
Diện tích tam giác ABC là:
4. 6 : 2 = 12 (cm2)
Vậy diện tích tam giác ABC là 12 cm2.
Câu 23:
Cho tam giác ABC cân tại A có BC = 6cm, đường cao AH = 4 cm. Kẻ
BM ^ AC. Tính BM.
 Xem đáp án
Xem đáp án
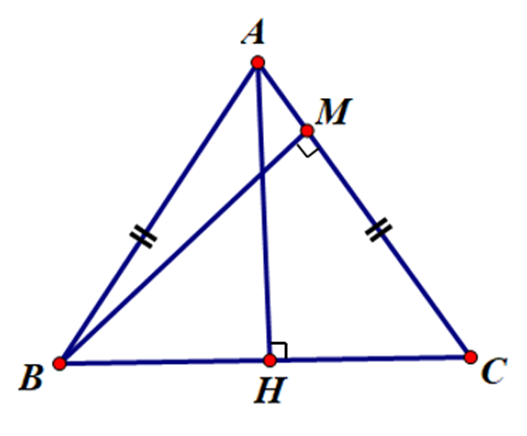
∆ABC cân tại A có AH ^ BC nên H là trung điểm của BC
\[ \Rightarrow HB = HC = \frac{1}{2}BC = 3\,\,cm\]
Xét ∆AHC vuông tại H có:
AC2 = AH2 + HC2 = 42 + 32 = 25 = 52
Þ AC = 5 cm
\[{S_{ABC}} = \frac{1}{2}BM.AC = \frac{1}{2}AH.BC = \frac{1}{2}.4.6 = 12\,\,\]
Þ BM . AC = 24
BM . 5= 24 = 4,8 (cm)
Vậy BM = 4,8 cm.
Câu 24:
Cho x, y là số nguyên \[(x \ne y)\] và n là số tự nhiên. Chứng minh xn – yn chia hết cho x – y.
 Xem đáp án
Xem đáp án
Vì xn – yn = (x – y)(xn-1 + xn-2y + xn-3y2 +…+ xyn-2 + yn-1)
Vì x – y chia hết cho x – y nên (x – y)(xn-1 + xn-2y + xn-3y2 +…+ xyn-2 + yn-1) chia hết cho x – y.
Vậy xn – yn chia hết cho x – y.
Câu 25:
Hai đường thẳng xy và zt cắt nhau tại O sao cho \[\widehat {xOz} = 70^\circ \].
a) Tính số đo các góc tạo thành
b) Vẽ tia Om là tia phân giác của \[\widehat {zOy}\] và tia On là tia đối của tia Om. Tính số đo \[\widehat {xOn}\], từ đó chỉ ra tia Ox không là tia phân giác của \[\widehat {zOn}\].
 Xem đáp án
Xem đáp án
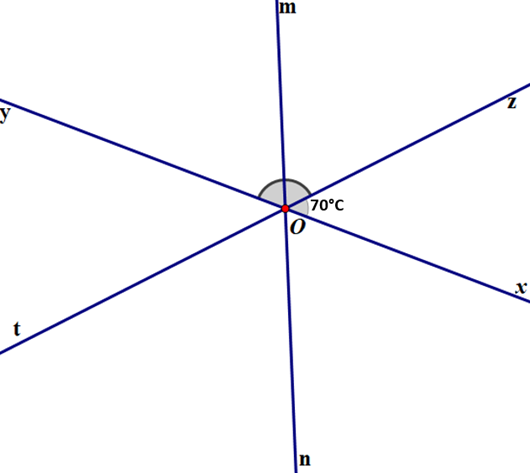
a) Ta có: \[\widehat {yOt} = \widehat {xOz} = 70^\circ \]
\[\widehat {xOt} = \widehat {yOz} = 180^\circ - 70^\circ = 110^\circ \]
b) Ta có: \[\widehat {xOn} = \widehat {yOm} = \frac{1}{2}\widehat {zOy\,}\, = 55^\circ \,\]
Vì \[\widehat {xOn} < \widehat {xOz}\,\,\,(55^\circ < 70^\circ )\] nên tia Ox không là tia phân giác của \[\widehat {zOn}\].
Vậy tia Ox không là tia phân giác của \[\widehat {zOn}\].
Câu 26:
Chứng minh rằng: 11n + 2 + 122n + 1 chia hết cho 133.
 Xem đáp án
Xem đáp án
11n + 2 + 122n + 1 = 121. 11n + 12. 144n
= (133 – 12). 11n + 12 . 144n = 133 . 11n + (144n – 11n) . 12
Ta có: 133. 11n chia hết 133;
144n – 11n chia hết (144 – 11) hay 144n – 11n chia hết cho 133.
⇒ 144n – 11n chia hết 133
Vậy 11n + 1 + 122n + 1.
Câu 27:
Có hai thùng chứa dầu, thùng nhỏ ít hơn thùng to là 4,5 lít dầu. Sau khi lấy 3,75 lít dầu từ thùng nhỏ thì thùng này còn lại 19,5 lít dầu. Hỏi lúc đầu cả hai thùng có bao nhiêu lít dầu?
 Xem đáp án
Xem đáp án
Ban đầu thùng nhỏ có số lít dầu là:
19,5 + 3,75 = 23,25 (l)
Ban đầu thùng to có số lít dầu là:
23,25 + 4,5 = 27,75 (l)
Ban đầu cả hai thùng có số lít dầu là:
23,25 + 27, 75 = 51 (l)
Đáp số: 51 lít dầu
Câu 28:
Một cửa hàng có hai thùng dầu, thùng to có 75,5 lít dầu, thùng bé có ít hơn thùng to 23,5 lít dầu. Số dầu đó được chứa vào các chai như nhau, mỗi chai có 0,75 lít dầu. Sau khi bán đi một số chai dầu thì cửa hàng còn lại 68 chai dầu. Hỏi cửa hàng đã bán được bao nhiêu lít dầu?
 Xem đáp án
Xem đáp án
Thùng bé có số lít dầu là
75,5 − 23,5 = 52 (lít)
Cả hai thùng có số lít dầu là:
75,5 + 52 = 127,5 (lít)
127,5 được chia vào số chai dầu là:
127,5 : 0,75 = 170 (chai)
Cửa hàng đã bán số chai dầu là:
170 – 68 = 102 (chai)
Cửa hàng đã bán được số lít dầu là:
0,75 × 102 = 76,5 (lít)
Đáp số: 76,5 lít
Câu 29:
Giải phương trình: |x – 0,7| = 1,3
 Xem đáp án
Xem đáp án
|x – 0,7| = 1,3
Trường hợp 1: x – 0,7 = 1,3
x = 1,3 + 0,7
x = 2
Trường hợp 2: x – 0,7 = –1,3
x = –1,3 + 0,7
x = –0,6
Vậy các giá trị x thỏa mãn phương trình là 2 và –0,6.
Câu 30:
Giải phương trình: |2x – 1,8| = 2,2
 Xem đáp án
Xem đáp án
|2x – 1,8| = 2,2
Trường hợp 1: 2x – 1,8 = 2,2
x = 2,2 + 1.8
x = 5
Trường hợp 2: 2x – 1,8 = –2,2
x = –2,2 + 1,8
x = –0,4
Vậy các giá trị x thỏa mãn phương trình là 5 và – 0,4.
Câu 31:
Một sân trường hình chữ nhật có chiều dài 120 m, chiều rộng bằng \[\frac{5}{6}\] chiều dài. Tính chu vi và diện tích của sân trường đó.
 Xem đáp án
Xem đáp án
Chiều rộng sân trường hình chữ nhật là:
\[120 \times \frac{5}{6} = 10\,0\,\,(m)\]
Chu vi sân trường hình chữ nhật là:
(120 + 100) × 2 = 440 (m)
Diện tích sân trường hình chữ nhật là:
120 × 100 = 12000 (m2)
Đáp số: Chu vi: 440 m;
Diện tích: 12000 m2
Câu 32:
Một sân vận động hình chữ nhật có chiều dài là 90 m, chiều rộng bằng \[\frac{2}{3}\] chiều dài. Tính chu vi, diện tích sân vận động đó.
 Xem đáp án
Xem đáp án
Chiều rộng sân vận động hình chữ nhật là:
\[90 \times \frac{2}{3} = 60\,\,(m)\]
Chu vi sân vận động hình chữ nhật là:
(90 + 60) × 2 = 300 (m)
Diện tích sân vận động hình chữ nhật là:
90 × 60 = 5400 (m2)
Đáp số: Chu vi: 300 m;
Diện tích: 5400 m2
Câu 33:
 Xem đáp án
Xem đáp án
Đổi \[3\frac{{65}}{{100}} = \frac{{365}}{{100}} = 3,65\]
Cả hai ngày cửa hàng đó bán được số tấn gạo là:
2,75 + 3,65 = 6,4 (tấn)
Đáp số: 6,4 tấn gạo.
Câu 34:
Một cửa hàng ngày đầu bán được \[3\frac{{48}}{{100}}\] tấn gạo, ngày thứ 2 bán được ít hơn ngày thứ nhất \[1\frac{{96}}{{100}}\] tấn gạo. Hỏi ngày thứ 2 cửa hàng đó bán được bao nhiêu tấn gạo?
 Xem đáp án
Xem đáp án
Đổi \[3\frac{{48}}{{100}} = \frac{{348}}{{100}} = 3,48\]
\[1\frac{{96}}{{100}} = \frac{{196}}{{100}} = 1,96\]
Ngày thứ 2 cửa hàng đó bán được số tấn gạo là:
3,48 – 1,96 = 1,52 (tấn)
Đáp số: 1,52 tấn gạo
Câu 35:
Một số khi chia cho 7 thì dư 3. Để được số chia hết cho 7 và thương tăng lên 1 đơn vị thì phải tăng số đó lên bao nhiêu đơn vị?
 Xem đáp án
Xem đáp án
Để thương tăng 1 đơn vị thì số bị chia phải tăng số đơn vị là:
1 × 7 = 7 (đơn vị)
Vì số đó chia 7 dư 3 nên để phép chia đó trở thành phép chia hết thì phải thêm vào số bị chia số đơn vị là:
7 − 3 = 4 (đơn vị)
Đáp số: 4 đơn vị.
Câu 36:
Một số khi chia cho 6 thì dư 4. Để được số chia hết cho 6 và thương tăng lên 2 đơn vị thì phải tăng số đó lên bao nhiêu đơn vị?
 Xem đáp án
Xem đáp án
Để thương tăng 2 đơn vị thì số bị chia phải tăng số đơn vị là:
2 × 6 = 12 (đơn vị)
Vì số đó chia 6 dư 4 nên để phép chia đó trở thành phép chia hết thì phải thêm vào số bị chia số đơn vị là:
12 − 4 = 8 (đơn vị)
Đáp số: 8 đơn vị.
Câu 37:
Nhà Minh có một mảnh đất hình chữ nhật có các kích thức là 4 m và 7 m. Để làm lối đi, bố Minh đã bớt mỗi kích thước đó đi x (m) (0 < x < 4) được khu vực trồng rau có chu vi là y (m).
a) Hãy lập công thức tính y theo x.
b) Trong trường hợp x = 0,5 m, hãy tính chu vi khu đất trồng rau.
 Xem đáp án
Xem đáp án
a) Chiều rộng mảnh đất hình chữ nhật sau khi cắt đi là:
4 − x (m)
Chiều dài mảnh đất hình chữ nhật sau khi cắt đi là:
7 – x (m)
Chu vi mảnh đất hình chữ nhật sau khi cắt đi là:
y = 2[(4 − x) + (7 − x)] = 2 (4 – x + 7 − x) = 2(11 − 2x) = 22 − 4x (1)
Vậy biểu thức liên hệ giữa x và y là y = 22 − 4x
b) Thay x = 0,5 vào (1) được: y = 22 − 4. 0,5 = 20 (m)
Vậy khi x = 0,5 m chu vi mảnh đất hình chữ nhật là 20 m.
Câu 38:
Tích sau tận cùng bằng mấy chữ số 0?
20 × 21 × 22 × 23 × . . . × 28 × 29
 Xem đáp án
Xem đáp án
20 × 21 × 22 × 23 × . . . × 28 × 29
Tích trên có 1 số tròn chục là 20 nên tích tận cùng bằng 1 chữ số 0
Ta lại có 25 = 5 × 5 nên 2 thừa số 5 này khi nhân với 2 số chẵn cho tích tận cùng bằng 2 chữ số 0.
Vậy tích trên tận cùng bằng 3 chữ số 0.
Câu 39:
Tích sau tận cùng bằng mấy chữ số 0?
30 × 31 × 32 × 33 × . . . × 38 × 39 × 40
 Xem đáp án
Xem đáp án
30 × 31 × 32 × 33 × . . . × 38 × 39 × 40
Tích trên có 2 số tròn chục là 20; 30 nên tích tận cùng bằng 2 chữ số 0
Ta lại có 35 = 5 × 7 nên thừa số 5 này khi nhân với 1 số chẵn cho tích tận cùng bằng 1 chữ số 0.
Vậy tích trên tận cùng bằng 3 chữ số 0.
Câu 40:
Ở một xã mỗi năm tăng thêm 4% so với số năm trước đó. Hiện nay có 2500 người. Hỏi hai năm nữa số dân xã đó là bao nhiêu?
 Xem đáp án
Xem đáp án
Một năm sau xã đó có số người là:
2500 : 100 × (100 + 4) = 2 600 (người)
2 năm sau xã đó có số người là
2600 : 100 × (100 + 4) = 2 704 (người)
Đáp số: 2704 người
Câu 41:
Ở một xã cứ 2 năm tăng thêm 5% so với số năm trước đó. Hai năm trướ có 2780 người. Hỏi hiện nay số dân xã đó là bao nhiêu?
 Xem đáp án
Xem đáp án
Hiện nay số dân xã đó là:
2780 : 100 × (100 + 5) = 2 919 (người)
Đáp số: 2 919 người.
Câu 42:
Cho x, y, z, t Î ℕ*. Chứng minh rằng:
\[M = \frac{x}{{x + y + z}} + \frac{y}{{x + y + t}} + \frac{z}{{y + z + t}} + \frac{t}{{x + z + t}}\] không phải số tự nhiên.
 Xem đáp án
Xem đáp án
\[M = \frac{x}{{x + y + z}} + \frac{y}{{x + y + t}} + \frac{z}{{y + z + t}} + \frac{t}{{x + z + t}}\]
Ta có:
\[\frac{x}{{x + y + z}} > \frac{x}{{x + y + z + t}}\]
\[\frac{y}{{x + y + t}} > \frac{y}{{x + y + z + t}}\]
\[\frac{z}{{y + z + t}} > \frac{z}{{x + y + z + t}}\]
\[\frac{t}{{x + z + t}} > \frac{t}{{x + y + z + t}}\]
\[ \Rightarrow M > \frac{x}{{x + y + z + t}} + \frac{y}{{x + y + z + t}} + \frac{z}{{x + y + z + t}} + \frac{t}{{x + y + z + t}}\]
Þ M > 1
Lại có:
\[\frac{x}{{x + y + z}} < \frac{{x + t}}{{x + y + z + t}}\]
\[\frac{y}{{x + y + t}} < \frac{{y + z}}{{x + y + z + t}}\]
\[\frac{z}{{y + z + t}} < \frac{{z + x}}{{x + y + z + t}}\]
\[\frac{t}{{x + z + t}} < \frac{{t + y}}{{x + y + z + t}}\]
\[ \Rightarrow M < \frac{{x + t}}{{x + y + z + t}} + \frac{{y + z}}{{x + y + z + t}} + \frac{{z + x}}{{x + y + z + t}} + \frac{{t + y}}{{x + y + z + t}}\]
\[ \Rightarrow M < \frac{{2(x + y + z + t)}}{{x + y + z + t}}\]
Þ M < 2
Do đó, 1 < M < 2
Vậy M không phải là số tự nhiên.
Câu 43:
Tìm 2 số tự nhiên a và b khác 0, biết a + b = 162 và ƯCLN(a, b) = 18.
 Xem đáp án
Xem đáp án
Vì ƯCLN(a, b) = 18 nên đặt a = 18k; b = 18q (ƯCLN(q, k) = 1; k < q)
Ta có: a + b = 162
18k + 18q = 162
18(k + q) = 162
k + q = 9
Ta có bảng:
|
k |
1 |
2 |
3 |
4 |
|
q |
8 |
7 |
6 |
5 |
|
a |
18 |
36 |
54 |
72 |
|
b |
144 |
126 |
108 |
90 |
Vậy các cặp số (a, b) thỏa mãn là {(18; 144); (36; 126); (54; 108); (72; 90)}
Câu 44:
 Xem đáp án
Xem đáp án
Vì ƯCLN(a, b) = 7 nên đặt a = 7k; b = 7q (ƯCLN(q, k) = 1; k < q)
Ta có: a + b = 35
7k + 7q = 35
7(k + q) = 35
k + q = 5
Ta có bảng:
|
k |
1 |
2 |
|
q |
4 |
3 |
|
a |
7 |
14 |
|
b |
28 |
21 |
Vậy các cặp số (a, b) thỏa mãn là {(7; 28); (14; 21)}
Câu 45:
Năm nay tuổi mẹ gấp 3 lần tuổi con, 12 năm trước tuổi mẹ gấp 7 lần tuổi con. Tìm tuổi mỗi người hiện nay.
 Xem đáp án
Xem đáp án
Ta có sơ đồ tuổi mẹ và con hiện nay:
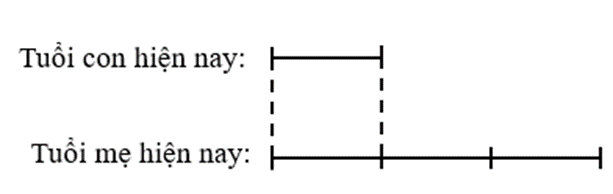
Hiện nay hiệu số tuổi của 2 mẹ con là:
3 − 1 = 2 (phần)
Ta có sơ đồ tuổi mẹ và con 12 năm trước:

Cách đây 12 năm hiệu số tuổi của 2 mẹ con là:
7 − 1 = 6 (phần)
Vì hiệu số tuổi của 2 người không đổi theo thời gian nên 2 lần tuổi con hiện nay bằng 6 lần tuổi con cách đây 12 năm.
Tuổi con hiện nay bằng số lần tuổi con cách đây 12 năm là:
6 : 2 = 3 (lần)
Ta có sơ đồ sau:
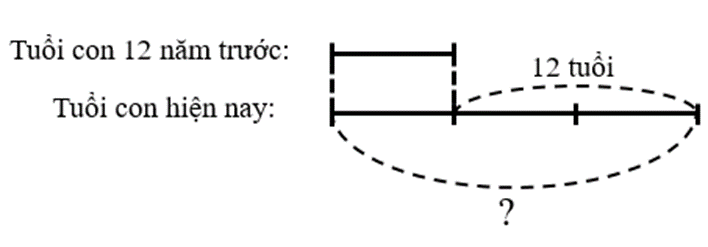
Nhìn vào sơ đồ ta có tuổi con hiện nay là:
12 : (3 − 1) × 3 = 18 (tuổi)
Tuổi mẹ hiện nay là:
18 × 3 = 54 (tuổi)
Đáp số: Mẹ: 54 tuổi;
Con: 18 tuổi
Câu 46:
Năm nay tuổi mẹ gấp 4 lần tuổi con, 8 năm trước tuổi mẹ gấp 10 lần tuổi con. Tìm tuổi mỗi người hiện nay.
 Xem đáp án
Xem đáp án
Ta có sơ đồ tuổi mẹ và con hiện nay:
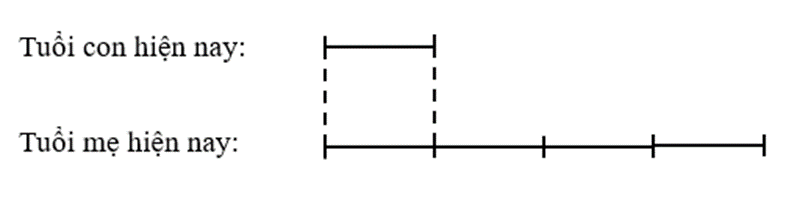
Hiện nay hiệu số tuổi của 2 mẹ con là:
4 − 1 = 3 (phần)
Ta có sơ đồ tuổi mẹ và con 12 năm trước:

Cách đây 8 năm hiệu số tuổi của 2 mẹ con là:
10 − 1 = 9 (phần)
Vì hiệu số tuổi của 2 người không đổi theo thời gian nên 3 lần tuổi con hiện nay bằng 9 lần tuổi con cách đây 8 năm.
Tuổi con hiện nay bằng số lần tuổi con cách đây 12 năm là:
9 : 3 = 3 (lần)
Ta có sơ đồ sau: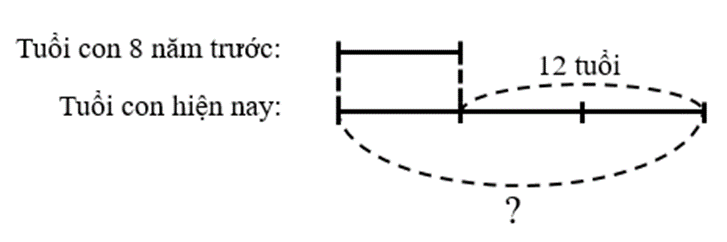
Nhìn vào sơ đồ ta có tuổi con hiện nay là:
8 : (3 − 1) × 3 = 12 (tuổi)
Tuổi mẹ hiện nay là:
12 × 4 = 48 (tuổi)
Đáp số: Con: 12 tuổi;
Mẹ: 48 tuổi
Câu 47:
Trung bình cộng của ba số bằng 24. Nếu gấp số thứ nhất lên 2 lần thì trung bình cộng của chúng bằng 28. Nếu gấp số thứ hai lên 3 lần thì trung bình cộng của chúng bằng 36. Tìm 3 số đó.
 Xem đáp án
Xem đáp án
Tổng 3 số là:
24 × 3 = 72
Tổng của số thứ 3 sau khi tăng số thứ nhất lên 2 lần là:
28 × 3 = 84
Số thứ nhất là:
84 – 72 = 12
Tổng 3 số sau khi tăng số thứ 2 lên 3 lần là:
36 × 3 = 108
Hai lần số thứ hai là:
108 – 72 = 36
Số thứ 2 là:
36 : 2 = 18
Số thứ ba là:
72 − (12 + 18) = 40
Đáp số: 12; 18; 40
Câu 48:
Trung bình cộng của ba số là 36. Nếu gấp số thứ nhất lên 2 lần thì trung bình cộng của chúng bằng 54. Nếu gấp số thứ hai lên 3 lần thì trung bình cộng của chúng bằng 46. Tìm ba số đó.
 Xem đáp án
Xem đáp án
Tổng 3 số lúc đầu là:
36 × 3 = 108
Tổng của 3 số sau khi tăng số thứ nhất lên 2 lần là:
54 × 3 = 162
Số thứ nhất là:
162 – 108 = 54
Tổng của 3 số sau khi tăng số thứ hai lên 3 lần là:
46 × 3 = 138
Hai lần số thứ 2 là:
138 – 108 = 30
Số thứ 2 là:
30 : 2 = 15
Số thứ 3 là:
108 – 54 – 15 = 39
Đáp số: 54; 15; 39
Câu 49:
Trung bình cộng của ba số là 120, biết rằng số thứ ba bằng \[\frac{1}{2}\] tổng của hai số còn lại. Tìm số thứ ba.
 Xem đáp án
Xem đáp án
Tổng 3 số là:
120 × 3 = 360
Ta có sơ đồ:
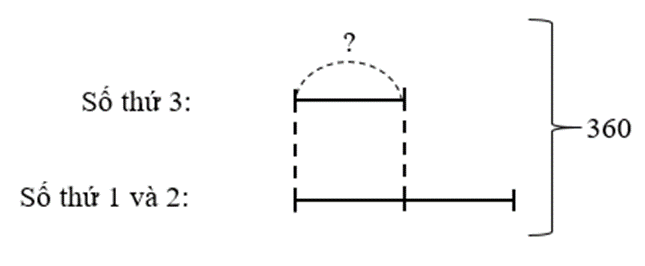
Số thứ 3 là:
360 : (1 + 2) = 120
Đáp số: 120
Câu 50:
Tìm 3 số có trung bình cộng bằng 120, biết rằng nếu viết thêm chữ số 0 vào bên phải số thứ nhất ta được số thứ hai và số thứ ba gấp 4 lần số thứ nhất.
 Xem đáp án
Xem đáp án
Tổng 3 số là:
120 × 3 = 360
Nếu viết thêm chữ số 0 vào bên phải số thứ nhất ta được số thứ hai nên số thứ hai gấp 10 lần số thứ nhất.
Ta có sơ đồ:
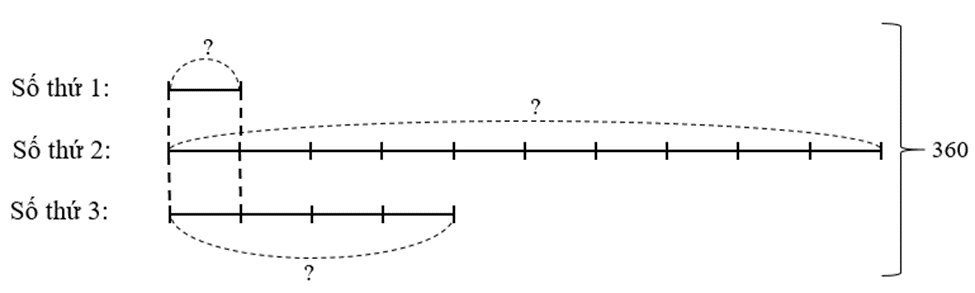
Số thứ nhất là:
360 : (1 + 10 + 4) = 24
Số thứ hai là:
24 × 10 = 240
Số thứ 3 là:
24 × 4 = 96
Đáp số: Số thứ nhất: 24;
Số thứ hai: 240;
Số thứ ba: 96
Câu 51:
Tâm cần đạt 100 điểm tuyệt đối ở bài kiểm tra Tiếng Anh cuối cùng để nâng điểm trung bình cả năm từ 84 lên 86. Hỏi có bao nhiêu bài kiểm tra Tiếng Anh trong năm?
 Xem đáp án
Xem đáp án
Gọi số bài kiểm tra của Tâm là x (bài) (x Î ℕ*)
Ta có phương trình:
84(x − 1) + 100 = 86x
Û 84x – 84 + 100 = 86x
Û 2x = 16
Û x = 8 (tmđk)
Vậy có 8 bài kiểm tra trong năm.
Câu 52:
Để được cấp chứng chỉ môn Anh trình độ A2 của một trung tâm ngoại ngữ, học viên phải trải qua 6 lần kiểm tra trắc nghiệm, thang điểm mỗi lần kiểm tra là 100 và phải đạt điểm trung bình từ 70 điểm trở lên. Qua 5 lần thi Hoa đạt điểm trung bình là 64,5 điểm. Hỏi trong lần kiểm tra cuối cùng Hoa phải đạt ít nhất là bao nhiêu điểm để được cấp chứng chỉ?
 Xem đáp án
Xem đáp án
Số điểm qua 5 lần thi của Hoa là:
64,5. 5 = 322,5 (điểm)
Số điểm tối thiểu Hoa cần đạt được để được cấp chứng chỉ là:
70. 6 = 420 (điểm)
Trong lần kiểm tra cuối cùng Hoa phải đạt ít nhất số điểm là:
420 – 322,5 = 97,5 (điểm)
Đáp số: 97,5 điểm
Câu 53:
Có một tờ giấy A4 lần thứ nhất cắt làm hai. Lần thứ hai cắt mỗi mảnh làm hai. Lần thứ ba cứ cắt đôi mỗi mảnh trước đó. Làm như vậy đến lần thứ 10 thì cắt bao nhiêu mảnh giấy?
 Xem đáp án
Xem đáp án
Lần thứ 1 có 21 mảnh
Lần thứ 2 có 22 mảnh
Lần thứ 3 có 23 mảnh
...
...
Suy ra lần thứ 10 có 210 = 1024 mảnh
Vậy sau 10 lần cắt có 1024 mảnh.
Câu 54:
Hoa gấp đôi tờ giấy rồi gấp tiếp như vậy 5 lần nữa. Sau đó, dùng đinh chọc thủng 1 lỗ ở giữa. Hỏi khi mở tờ giấy sẽ có bao nhiêu lỗ?
 Xem đáp án
Xem đáp án
Số lần Hoa gấp đôi giấy là:
1 + 5 = 6 (lần)
Lần thứ 1 gấp đôi được 21 lớp giấy
Lần thứ 2 gấp đôi được 22 lớp giấy
...
Lần thứ 6 gấp đôi được 26 = 64 lớp giấy
Vì có 64 lớp giấy nên khi chọc đinh tạo ra 64 lỗ.
Vậy có tất cả 64 lỗ.
Câu 55:
Giải phương trình:
(6x – 2)10 = (6x – 2)20
(6x – 2)10 = (6x – 2)20
 Xem đáp án
Xem đáp án
(6x – 2)20 – (6x – 2)10 = 0
Û (6x – 2)10[(6x – 2)10 – 1] = 0
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{(6x - 2)}^{10}} = 0}\\{{{(6x - 2)}^{10}} - 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{(6x - 2)}^{10}} = 0}\\{{{(6x - 2)}^{10}} = 1}\end{array}} \right.\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{6x - 2 = 0}\\{6x - 2 = 1}\\{6x - 2 = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{1}{3}}\\{x = \frac{1}{2}}\\{x = \frac{1}{6}}\end{array}} \right.\]
Vậy tập nghiệm của phương trình là \[S = \left\{ {\frac{1}{2};\,\,\frac{1}{3};\,\,\frac{1}{6}} \right\}\].
Câu 56:
Giải phương trình: (3x – 2)5 = (3x – 2)10.
 Xem đáp án
Xem đáp án
(3x – 2)5 = (3x – 2)10
Û (3x – 2)5 – (3x – 2)10 = 0
Û (3x – 2)5[(3x – 2)5 – 1] = 0
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{(3x - 5)}^5} = 0}\\{{{(3x - 5)}^5} - 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{(3x - 5)}^5} = 0}\\{{{(3x - 5)}^5} = 1}\end{array}} \right.\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x - 5 = 0}\\{3x - 5 = 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{5}{3}}\\{x = 2}\end{array}} \right.\]
Vậy tập nghiệm của phương trình là \[S = \left\{ {\frac{5}{3};\,\,2} \right\}\]
Câu 58:
Số 180 chia hết cho những số nào?
 Xem đáp án
Xem đáp án
Ta có: 180 = 22. 32. 5
Vậy số 180 chia hết cho các số 1; 2; 3; 4; 5; 6; 9; 10; 12; 15; 18; 20; 30; 36; 45; 60; 90 và 180.
Câu 59:
Cho a là số có một chữ số, b là số có hai chữ số, c là số có ba chữ số. Trung bình cộng của ba số đó là 369. Tìm a, b, c.
 Xem đáp án
Xem đáp án
Tổng của 3 số đó là:
369 × 3 = 1107
Ta có: 1107 = 1000 + 100 + 7 = 999 + 1 + 99 + 1 + 7 = 999 + 99 + 9
Suy ra 3 chữ số a, b, c lần lượt là: 9; 99; 999 (vì 9; 99 và 999 đều là số lớn nhất có 1, 2 và 3 chữ số. Nếu có một số giảm xuống thì 1 hoặc 2 số còn lại phải tăng nên, khi đó không thỏa mãn điều kiện bài toán)
Vậy 2 số a, b, c là 9, 99, 999.
Câu 60:
Một cửa hàng có 2,5 tấn gạo. Buổi sáng bán được \[\frac{1}{5}\] số gạo cửa hàng. Hỏi cửa hàng còn lại bao nhiêu tạ gạo?
 Xem đáp án
Xem đáp án
Buổi sáng cửa hàng bán được số tấn gạo là:
2,5 : 5 × 1 = 0,5 (tấn)
Cửa hàng còn lại số gạo là:
2,5 - 0,5 = 2 (tấn) = 20 (tạ)
Đáp số: 20 tạ gạo.
Câu 61:
Một cửa hàng cả ngày bán được 450 tấn gạo, trong đó buổi sáng bán được 65% số gạo. Hỏi buổi chiều của hàng đó bán được bao nhiêu tấn gạo?
 Xem đáp án
Xem đáp án
Buổi sáng bán được số gạo là:
450 × 65 : 100 = 292,5 (tấn)
Buổi chiều bán được số gạo là:
450 – 292,5 = 157,5 (tấn)
Đáp số: 157,5 tấn gạo.
Câu 62:
Cho 3a + 2b chia hết cho 17. Chứng minh rằng 10a + b chia hết cho 17.
 Xem đáp án
Xem đáp án
Ta có: 2(10a + b) - (3a + 2b) = 20a + 2b - 3a - 2b = 17a.
Vì 17 ⋮ 17 nên 17a ⋮ 17.
Do đó: 2(10a + b) - (3a +2b) ⋮ 17
Vì (3a + 2b) ⋮ 17 nên 2(10a + b) ⋮ 17
Mà (2, 17) = 1 nên 10a + b ⋮ 17
Vậy nếu 3a + 2b ⋮ 17 thì 10a + b ⋮ 17.
Câu 63:
Chứng minh a + 2b chia hết cho 3 khi và chỉ khi b + 2a cũng chia hết cho 3.
 Xem đáp án
Xem đáp án
Ta có :
3a + 3b và a + 2b đều chia hết cho 3
Suy ra (3a + 3b) − (a + 2b) ⋮ 3
Do đó, 2a + b ⋮ 3 (đpcm)
Vậy a + 2b chia hết cho 3 khi và chỉ khi b + 2a cũng chia hết cho 3.
Câu 64:
Cho hình H tạo bởi hình chữ nhật ABCD và hình bình hành BEFC như hình vẽ. Tính diện tích hình H.
 Xem đáp án
Xem đáp án
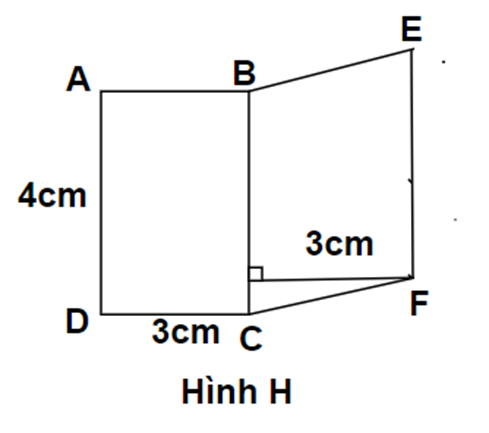
Diện tích của hình chữ nhật ABCD là :
4 × 3 = 12 (cm2)
Diện tích của hình bình hành BEFC là :
4 × 3 = 12 (cm2)
Diện tích của hình H là :
12 + 12 = 24 (cm2)
Đáp số: 24 cm2
Câu 65:
Cho Parabol (P): y = x2 và đường thẳng (d): y = mx – m + 1
a) Tìm toạ độ giao điểm của (P) và (d) khi m = 4
b) Tìm m để (d) cắt (P) tạo hai điểm phân biệt có hoành độ thoả mãn x1 = 9x2
 Xem đáp án
Xem đáp án
a) Xét phương trình hoành độ giao điểm:
x2 = mx – m + 1
Û x2 – mx + m – 1 = 0 (1)
Thay m = 4 vào phương trình (1) ta có:
x2 – 4x + 3 = 0
Û x2 – x – 3x + 3 = 0
Û x(x – 1) – 3(x – 1) = 0
Û (x – 1)(x – 3) = 0
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - 1 = 0}\\{x - 3 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 3}\end{array}} \right.\]
\[ \Rightarrow \left[ {\begin{array}{*{20}{c}}{y = 1}\\{y = 9}\end{array}} \right.\]
Vậy toạ độ giao điểm của (P) và (d) khi m = 4 là A(1; 1) và B(3; 9).
b) Phương trình: x2 – mx + m – 1 = 0 (1)
Û x2 – 1 – mx + m = 0
Û (x – 1)(x + 1) – m(x – 1) = 0
Û (x – 1)(x + 1 – m) = 0
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - 1 = 0}\\{x + 1 - m = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = m - 1}\end{array}} \right.\]
Để (d) cắt (P) tạo hai điểm phân biệt thì phương trình (1) phải có 2 nghiệm phân biệt.
Do đó, \[m - 1 \ne 1 \Leftrightarrow m \ne 2\]
Ta có: x1 = 9x2
Trường hợp 1: 1 = 9(m – 1)
Û 1 = 9m – 9
Û 9m = 10
Û \[m = \frac{{10}}{9}\] (tmđk)
Trường hợp 2: m – 1 = 9. 1
Û m – 1 = 9
Û m = 10 (tmđk)
Vậy tập hợp các giá trị m thoả mãn đề bài là \[S = \left\{ {\frac{{10}}{9};10} \right\}\].
Câu 66:
Hai số có tổng là 340, hiệu là 240. Tìm số bé
 Xem đáp án
Xem đáp án
Ta có sơ đồ:
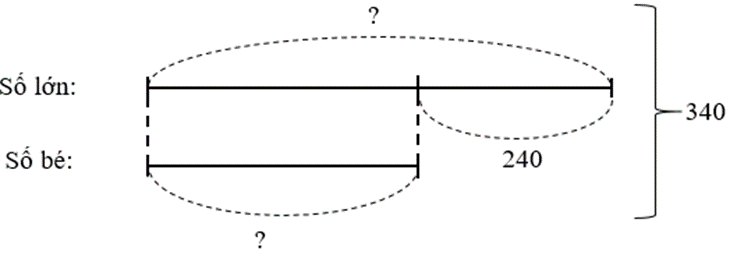
Số bé là:
(340 – 240) : 2 = 50
Đáp số: 50
Câu 67:
Tìm 2 số có hiệu là 120. Nếu bớt đi mỗi số 15 đơn vị thì được tổng mới là 270. Tìm số lớn.
 Xem đáp án
Xem đáp án
Tổng hai số là:
270 + 15 ´ 2 = 300
Ta có sơ đồ:
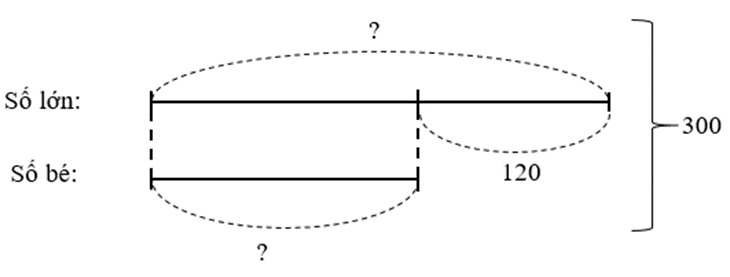
Số lớn là:
(300 + 120) : 2 = 210
Đáp số: 210
Câu 68:
Hồng và Lan cùng hái hoa, biết số hoa của Lan bằng \[\frac{3}{5}\] số hoa của Hồng. Sau khi hai bạn cùng hái thêm 15 bông, lúc này số hoa của Lan bằng \[\frac{9}{{13}}\] số hoa của Hồng. Tính số hoa mỗi bạn lúc đầu?
 Xem đáp án
Xem đáp án
Vì ban đầu số hoa của Lan bằng \[\frac{3}{5}\] số hoa của Hồng
Ta có sơ đồ:

Hiệu số phần bằng nhau là:
5 – 3 = 2 (phần)
Sau khi hai bạn hái thêm 15 bông hoa thì số hoa của Lan bằng \[\frac{9}{{13}}\] số hoa của Hồng.
Ta có sơ đồ:
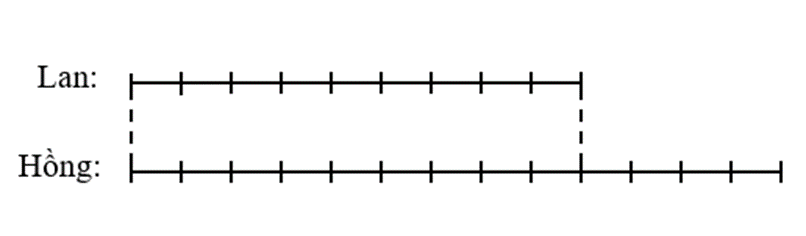
Hiệu số phần bằng nhau là:
13 – 9 = 4 (phần)
Khi hai bạn cùng hái thêm 15 bông hoa thì hiệu số phần tăng lên là:
4 : 2 = 2 (lần)
Số hoa của Lan ban đầu là:
15 × 2 = 30 (bông hoa)
Số hoa của Hồng ban đầu là:
30 : 3 × 5 = 50 (bông hoa)
Đáp số: Lan: 30 bông hoa;
Hồng: 50 bông hoa
Câu 69:
Biểu diễn các hỗn số sau dưới dạng số thập phân:
a) \[5\frac{{11}}{{12}}\]
b) \[7\frac{2}{{17}}\]
 Xem đáp án
Xem đáp án
a) \[5\frac{{11}}{{12}} = \frac{{5 \times 12 + 11}}{{12}} = \frac{{60 + 11}}{{12}} = \frac{{71}}{{12}}\]
b) \[7\frac{2}{{17}} = \frac{{7 \times 17 + 2}}{{17}} = \frac{{119 + 2}}{{17}} = \frac{{121}}{{17}}\]
Câu 70:
Biểu diễn các số thập phân sau dưới dạng hỗn số:
a) \[\frac{{126}}{{15}}\]
b) \[\frac{{1267}}{{41}}\]
 Xem đáp án
Xem đáp án
a) \[\frac{{126}}{{15}} = \frac{{120 + 6}}{{15}} = \frac{{8 \times 15 + 6}}{{15}} = 8 + \frac{6}{{15}} = 8\frac{6}{{15}}\]
b) \[\frac{{1267}}{{41}} = \frac{{1230 + 37}}{{41}} = \frac{{30 \times 41 + 37}}{{41}} = 30 + \frac{{37}}{{41}} = 30\frac{{37}}{{41}}\]
Câu 71:
Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD. Gọi M và N lần lượt là trung điểm của OB và CD. Chứng minh rằng: \[\widehat {AMN} = 90^\circ \].
 Xem đáp án
Xem đáp án
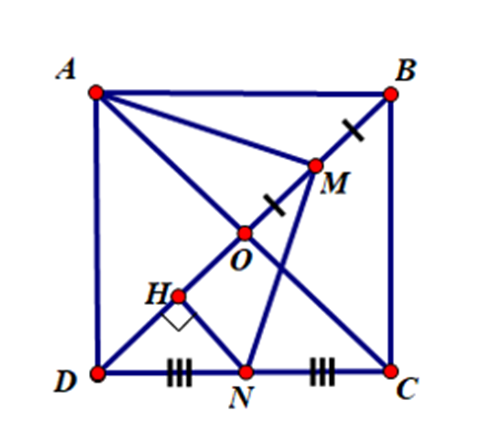
Kẻ NH ^ OD
ABCD là hình vuông nên AC ^ BD và AC = BD
Þ NH // OC
Xét ΔOCD có:
NC = ND (vì N là trung điểm của CD)
NH // OC
Þ NH là đường trung bình của ΔOCD
Þ H là trung điểm của OD và \[NH = \frac{1}{2}OC\]
Þ NH = OM
Ta có:
\[HM = OM + OH = \frac{1}{2}OB + \frac{1}{2}OD = \frac{1}{2}BD\]
Þ HM = OA
Xét ΔOMA và ΔHNM có:
\[\widehat H = \widehat O = 90^\circ \]
NH = OM
HM = OA
ΔHNM = ΔOMA (c.g.c)
\[ \Rightarrow \widehat {HMN} = \widehat {OAM}\]
Do đó:
\[\widehat {AMN} = \widehat {AMO} + \widehat {HMN} = \widehat {AMO} + \widehat {OAM} = 90^\circ \]
Vậy AM ^ MN.
Câu 72:
Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD. Gọi M và N lần lượt là trung điểm của OB và CD. Chứng minh rằng bốn điểm A, M, N, D cùng thuộc một đường tròn.
 Xem đáp án
Xem đáp án
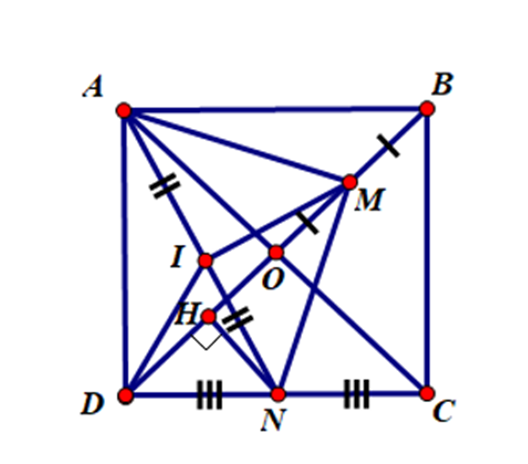
Kẻ NH ^ OD
ABCD là hình vuông nên AC ^ BD và AC = BD
Þ NH // OC
Xét ΔOCD có:
NC = ND (vì N là trung điểm của CD)
NH // OC
Þ NH là đường trung bình của ΔOCD
Þ H là trung điểm của OD và \[NH = \frac{1}{2}OC\]
Þ NH = OM
Ta có:
\[HM = OM + OH = \frac{1}{2}OB + \frac{1}{2}OD = \frac{1}{2}BD\]
Þ HM = OA
Xét ΔOMA và ΔHNM có:
\[\widehat H = \widehat O = 90^\circ \]
NH = OM
HM = OA
ΔHNM = ΔOMA (c.g.c)
\[ \Rightarrow \widehat {HMN} = \widehat {OAM}\]
Do đó:
\[\widehat {AMN} = \widehat {AMO} + \widehat {HMN} = \widehat {AMO} + \widehat {OAM} = 90^\circ \]
Gọi I là trung điểm của AN
Xét ΔAMN vuông tại M có I là trung điểm của AN
\[ \Rightarrow IM = IN = IA = \frac{1}{2}AN\]
Xét ΔADN vuông tại D có I là trung điểm của AN
\[ \Rightarrow ID = IN = IA = \frac{1}{2}AN\]
Do đó: IA = IM = IN = ID hay 4 điểm A, M, N, D cùng thuộc đường tròn tâm I, bán kính IA.
Vậy bốn điểm A, M, N, D cùng thuộc một đường tròn.
Câu 73:
 Xem đáp án
Xem đáp án
Vì mỗi năm mỗi người tăng lên 1 tuổi.
Tổng tuổi hiện nay của hai mẹ con là:
5 ´ 2 + 34 = 44 (tuổi)
Ta có sơ đồ:

Tuổi con là :
(44 – 22) : 2 = 11 (tuổi)
Tuổi mẹ là :
11 + 22 = 33 (tuổi)
Đáp số: 11 tuổi; 33 tuổi
Câu 74:
Mẹ hơn con 30 tuổi. Biết rằng 3 năm sau tuổi mẹ và tuổi con cộng lại được 54 tuổi. Tính tuổi hiện nay của mỗi người.
 Xem đáp án
Xem đáp án
Vì mỗi năm mỗi người tăng lên 1 tuổi.
Tổng tuổi hiện nay của hai mẹ con là:
54 – 3 ´ 2 = 48 (tuổi)
Ta có sơ đồ:
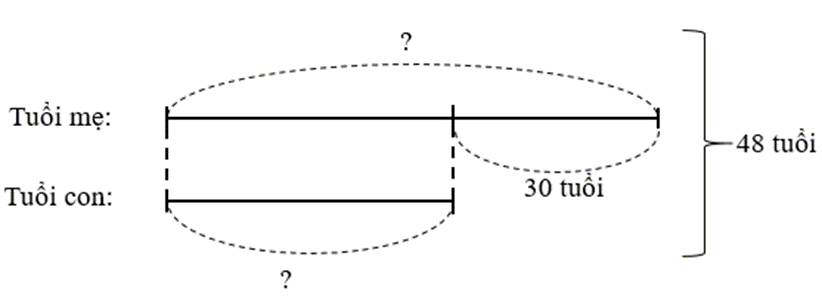
Tuổi con là :
(48 – 30) : 2 = 9 (tuổi)
Tuổi mẹ là :
9 + 30 = 39 (tuổi)
Đáp số: 9 tuổi; 39 tuổi
Câu 75:
Một bể nước hình hộp chữ nhật có chiều dài 3 m, chiều cao 1,5 m. Lúc đầu bể không có nước. Sau khi đổ vào bể 90 thùng nước, mỗi thùng chứa 30 lít thì mực nước của bể cao 0,4 m. Hỏi thể tích của bể là bao nhiêu?
 Xem đáp án
Xem đáp án
Thể tích nước đổ vào là:
90 ´ 30 = 2700 (lít) = 2,7 (m3)
Chiều rộng của bể nước là:
2,7 : (3 ´ 0,4) = 2,25 (m)
Thể tích của bể nước là:
2,25 ´ 3 ´ 1,5 = 10,125 (m3)
Đáp số: 10,125 m3.
Câu 76:
Một bể nước hình hộp chữ nhật có chiều dài 2 m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít thì mực nước của bể cao 0,8 m.
a) Tính chiều rộng của bể nước
b) Người ta đổ thêm vào bể 60 thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?
 Xem đáp án
Xem đáp án
a) Thể tích nước đổ vào là:
120 ´ 20 = 2400 (lít) = 2,4 (m3)
Chiều rộng của bể nước là:
2,4 : (2 ´ 0,8) = 1,5 (m)
b) Thể tích của bể nước là:
2400 + 60 ´ 20 = 3600 (lít) = 3,6 (m3)
Chiều cao của bể nước:
3,6 : (2 ´ 1,5) = 1,2 (m)
Đáp số: a) 1,5 m;
b) 1,2 m.
Câu 77:
Một ô tô du lịch đi từ thành phố Hồ Chí Minh lúc 7 giờ 30 phút và đến Đà Lạt lúc 14 giờ 30 phút, biết giữa đường ô tô có nghỉ 1 giờ 30 phút. Vận tốc của ô tô này là 49,6 km/giờ. Tính độ dài quãng đường từ thành phố Hồ Chí Minh đến Đà Lạt.
 Xem đáp án
Xem đáp án
14 giờ 30 phút = 14,5 giờ
7 giờ 30 phút = 7,5 giờ
1 giờ 30 phút = 1,5 giờ
Thời gian ô tô đi từ thành phố Hồ Chí Minh đến Đà Lạt mà không tính thời gian nghỉ là:
14,5 – 7,5 – 1,5 = 5,5 (giờ)
Độ dài quãng đường là:
49,6 ´ 5,5 = 272,8 (km)
Đáp số: 272,8 km
Câu 78:
Một xe ô tô đi từ 5 giờ 30 phút đến 7 giờ đi được quãng đường 52,5 km. Tính vận tốc của xe ô tô, biết rằng giữa đường lái xe có dừng lại đổ xăng hết 15 phút.
 Xem đáp án
Xem đáp án
5 giờ 30 phút = 5,5 giờ
15 phút = 0,25 giờ
Thời gian ô tô đi quãng đường mà không tính thời gian đổ xăng là:
7 – 5,5 – 0,25 = 1,25 (giờ)
Độ dài quãng đường là:
52,5 : 1,25 = 42 (km/h)
Đáp số: 42 km/h
Câu 79:
Người ta thu hoạch ở hai thửa ruộng được 3 tấn 6 tạ thóc. Ở thửa ruộng thứ nhất thu hoạch được ít hơn thửa ruộng thứ hai 4 tạ thóc. Hỏi mỗi thửa ruộng, người ta thu hoạch được bao nhiêu ki lô gam thóc?
 Xem đáp án
Xem đáp án
Đổi: 3 tấn 6 tạ = 3600 kg;
4 tạ = 400 kg.
Ta có sơ đồ:

Thửa ruộng thứ nhất thu được số thóc là:
(3 600 – 400) : 2 = 1 600 (kg)
Thửa ruộng thứ hai thu được số thóc là:
3 600 – 1 600 = 2 000 (kg)
Đáp số: 1 600 kg; 2 000 kg
Câu 80:
Người ta thu hoạch từ hai thửa ruộng được 8 tấn 9 tạ thóc. Thu hoạch ở thửa ruộng thứ nhất được nhiều hơn thửa ruộng thứ hai 13 tạ thóc. Hỏi thu hoạch ở mỗi thửa ruộng được bao nhiêu ki-lô-gam thóc?
 Xem đáp án
Xem đáp án
Đổi 8 tấn 9 tạ = 8 900 kg;
13 tạ = 1 300 kg.
Ta có sơ đồ:
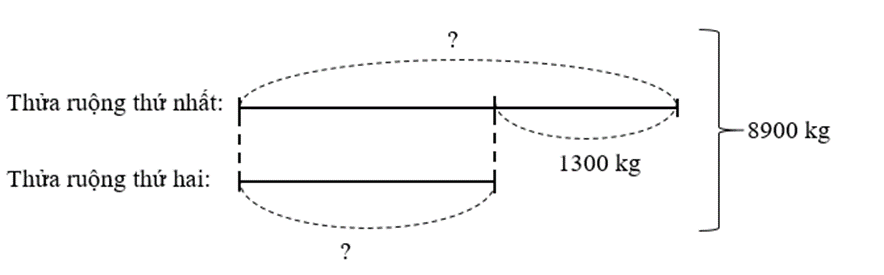
Thửa ruộng thứ nhất thu được số thóc là:
(8900 + 1300) : 2 = 5100 (kg)
Thửa ruộng thứ hai thu được số thóc là:
5100 – 1300 = 3800 (kg)
Đáp số: Thửa ruộng thứ 1: 5100 kg;
Thửa ruộng thứ 2: 3800 kg.
Câu 81:
Phúc và Quang cùng khởi hành 1 lúc từ nhà mình và đi về phía nhau. Phúc đi nhanh bằng \[\frac{4}{3}\] lần Quang và họ gặp nhau sau 72 phút. Phúc phải khởi hành sau Quang bao lâu để họ gặp nhau ở chính giữa quãng đường?
 Xem đáp án
Xem đáp án
Vì Phúc đi nhanh bằng \[\frac{4}{3}\] lần Quang nên trong 72 phút, Phúc đi được \[\frac{4}{7}\] quãng đường và Quang đi được \[\frac{3}{7}\] quãng đường.
Phúc đi cả quãng đường trong thời gian là:
\[72:\frac{4}{7} = 126\,\,(ph\'u t)\]
Phúc đi nửa quãng đường trong thời gian là:
126 : 2 = 63 (phút)
Quang đi cả quãng đường trong thời gian là:
\[72:\frac{3}{7} = 168\,\,(ph\'u t)\]
Quang đi nửa quãng đường trong thời gian là:
168 : 2 = 84 (phút)
Do đó, muốn gặp Quang tại chính giữa đường thì Phúc phải khởi hành sau Quang số phút là:
84 – 63 = 21 (phút)
Đáp số: 21 phút
Câu 82:
An và Huệ cùng khởi hành 1 lúc từ nhà mình và đi về phía nhau. An đi nhanh bằng \[\frac{3}{5}\] lần Huệ nên họ gặp nhau sau 45 phút. An phải khởi hành trước Huệ bao lâu để họ gặp nhau ở \[\frac{1}{4}\] quãng đường tính từ nhà Huệ?
 Xem đáp án
Xem đáp án
Vì An nhanh bằng \[\frac{3}{5}\] lần Huệ nên trong 45 phút, An đi được \[\frac{3}{8}\] quãng đường và Huệ đi được \[\frac{5}{8}\] quãng đường.
Họ gặp nhau ở \[\frac{1}{4}\] quãng đường tính từ nhà Huệ nên khi đó An đi được \[\frac{3}{4}\] quãng đường và Huệ đi được \[\frac{1}{4}\] quãng đường.
An đi cả quãng đường trong thời gian là:
\[45:\frac{3}{8} = 120\,\,(ph\'u t)\]
An đi \[\frac{3}{4}\] quãng đường trong thời gian là:
\[120 \times \frac{3}{4} = 90\,(ph\'u t)\]
Huệ đi cả quãng đường trong thời gian là:
\[45:\frac{5}{8} = 72\,\,(ph\'u t)\]
Huệ đi \[\frac{1}{4}\] quãng đường trong thời gian là:
\[72 \times \frac{1}{4} = 18\,\,(ph\'u t)\]
An phải khởi hành trước Huệ số phút để họ gặp nhau ở \[\frac{1}{4}\] quãng đường tính từ nhà
Huệ là:
90 – 18 = 72 (phút)
Đáp số: 72 phút
Câu 83:
Học sinh lớp 6A có từ 40 đến 50 em. Khi xếp hàng 3 hoặc 5 đều dư 2 em. Tìm số học sinh lớp 6A.
 Xem đáp án
Xem đáp án
Vì khi xếp hàng 3 hoặc hàng 5 đều dư 2 em nên nếu bỏ đi 2 em thì số học sinh lớp 6A chia hết cho cả 3 và 5.
BC(3, 5) = {15, 30, 45,…}
Vì số học sinh lớp 6A từ 40 đến 50 em nên số học sinh lớp 6A là 45 em.
Đáp số: 45 em
Câu 84:
Học sinh khối 7 một trường có từ 200 đến 300 em. Nếu xếp hàng 4, 5 hoặc 7 đều dư 1 em. Tìm số học sinh khối 7 của trường.
 Xem đáp án
Xem đáp án
Vì xếp hàng 4, 5 hoặc 7 đều dư 1 em nên nếu trừ đi 1 em thì số học sinh khối 7 chia hết cho cả 4, 5 và 7.
BC(4, 5, 7) = {140, 280, 420,…}
Vì học sinh khối 7 một trường có từ 200 đến 300 em nên số học sinh khối 7 của trường đó là 280 em.
Đáp số : 280 em
Câu 85:
Cho tam giác ABC cân tại A có AB = 15 cm, đường cao AH = 9 cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
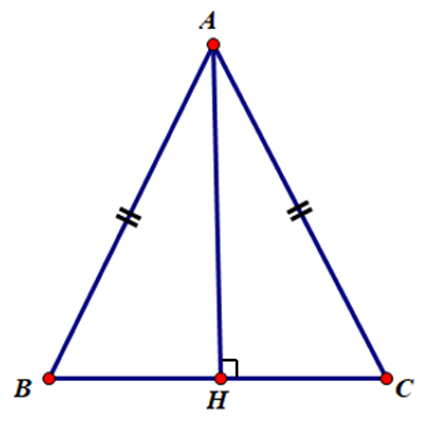
ΔABC cân tại A nên AB = AC = 15 cm.
Xét tam giác ABH vuông tại H:
\[\sin \widehat B = \frac{{AH}}{{AB}} = \frac{9}{{15}}\]
Theo định lý sin ta có:
\[112 \times \frac{3}{4} = 84\,\,(ph\'u t)\]
\[ \Rightarrow R = \frac{{AC}}{{2\sin \widehat B}} = \frac{{15}}{{2.\frac{9}{{15}}}} = 12,5\,\,\,(cm)\]
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 12,5 cm.
Câu 86:
Cho tam giác ABC cân tại A có BC = 12 cm, đường cao AH = 8 cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
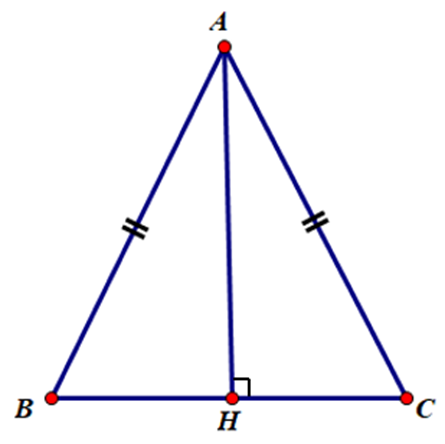
ΔABC cân tại A, AH ^ BC nên H là trung điểm của BC.
\[BH = HC = \frac{1}{2}BC = 6\,\,cm\]
Áp dụng định lý Pythagore cho ABH vuông tại H:
AB2 = AH2 + HB2 = 82 + 62 = 100 = 102
Þ AB = 10 cm
Xét tam giác ABH vuông tại H:
\[\sin \widehat B = \frac{{AH}}{{AB}} = \frac{8}{{10}} = \frac{4}{5}\]
Theo định lý sin ta có: \[\frac{{AC}}{{\sin \widehat B}} = 2R\]
\[ \Rightarrow R = \frac{{AC}}{{2\sin \widehat B}} = \frac{{10}}{{2.\frac{4}{5}}} = 6,25\,\,\,(cm)\]
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 6,25 cm.
Câu 87:
Cho A = 1 + 10 + 102 + 33 + … + 10200. Tìm số dư khi chia A cho 111.
 Xem đáp án
Xem đáp án
A = 1 + 10 + 102 + 33 + … + 10200
= (1 + 10 + 102) + (103 + 104 + 105) + .... + (10198 + 3199 + 3200)
= (1 + 10 + 102) + 103(1 + 10 + 102) +.... + 10198(1 + 10 + 102)
= (1 + 10 + 102)(1 + 103 + .... + 10198)
= 111(1 + 103 + .... + 10198)
Vì 111 chia hết cho 111 và (1 + 103 + .... + 10198) ∈ ℕ*
Nên 111(1 + 103 + .... + 10198) chia hết cho 111
Vậy A chia hết cho 111.
