Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 14)
-
2072 lượt thi
-
53 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Để lát một căn phòng hình chữ nhật có chiều dài 12m, chiều rộng 8m, người ta dùn gạch men hình vuông có cạnh 4 dm. Hỏi cần bao nhiêu viên gạch để lát kín căn phòng đó?
 Xem đáp án
Xem đáp án
Diện tích căn phòng đó là:
12 . 8 = 96 (m²)
Diện tích một viên gạch là:
40 . 40 =1600 (cm²)
Đổi: 1600 cm² = 0,16m²
Số gạch dùng để lát nền là:
96 : 0,16 = 600 (viên).
Đáp số: 600 viên gạch.
Câu 2:
Tìm x biết x chia hết cho 15 và 12; biết 0 < x < 150.
 Xem đáp án
Xem đáp án
Vì x chia hết cho 15, 12 nên x thuộc BCNN (15,12)
Ta có 15 = 3.5
12 = 22 . 3
Vậy BCNN (15, 12) = 22 . 3 . 5 = 60
Vì 0 < x < 150 nên x = 60 hoặc x = 120.
Vậy x = 60 hoặc x = 120.
Câu 3:
Tìm số tự nhiên x biết: 70 ⋮ x, 84 ⋮ x và x > 8.
 Xem đáp án
Xem đáp án
70 ⋮ x, 84 ⋮ x và x > 8
Vì 70 ⋮ x, 84 ⋮ x nên x ∈ ƯC(70; 84)
Ta có: 70 = 2. 5. 7
84 = 22. 3. 7
ƯCLN(70; 84) = 2 . 7 = 14
ƯC (70; 84) = {1; 2; 7; 14}
Vì x > 8 nên x = 14.
Vậy x = 14.
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC.
a) Chứng minh AEHF là hình chữ nhật.
 Xem đáp án
Xem đáp án
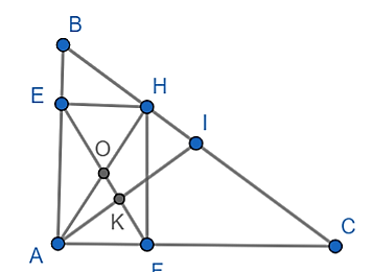
a) Xét tứ giác AEHF có:
= 90°
= 90°
Suy ra: AEHF là hình chữ nhật.
Câu 5:
b) Gọi O là trung điểm của AH. Chứng minh rằng: E,F,O thẳng hàng.
 Xem đáp án
Xem đáp án
b) Ta có: AEHF là hình chữ nhật
O là trung điểm của AH nên O là trung điểm EF
Vậy E, O, F thẳng hàng.
Câu 6:
c) Chứng minh rằng: .
 Xem đáp án
Xem đáp án
c) Ta có: AE = OE (vì AH = EF)
Suy ra tam giác AOE cân tại O
Suy ra:
Mà = 90°
= 90°
Suy ra:
Vậy .
Câu 7:
d) Gọi I là trung điểm của BC, chứng minh AI vuông góc với EF.
 Xem đáp án
Xem đáp án
d) Xét tam giác ABC vuông tại A có AI là trung tuyến
⇒ AI = IC = ( tính chất trung tuyến ứng với cạnh huyền bằng cạnh huyền)
Suy ra: tam giác AIC cân tại I
⇒
Mà (chứng minh trên)
⇒
Lại có: = 90°
= 90°
Gọi giao điểm của AI và EF là K
Xét tam giác AKE có:
= 90°
⇒ = 180° – 90° = 90°
Vậy AK vuông góc KE hay AI ⊥ EF tại K.
Câu 8:
Để lát nền căn phòng hình chữ nhật có chiều dài 12m, chiều rộng bằng chiều dài. Để lát nền căn phòng đó, người ta dùng loại gạch men hình vuông cạnh 8dm. Hỏi căn phòng được lát bằng bao nhiêu viên gạch men đó? (phần gạch vữa không đáng kể).
 Xem đáp án
Xem đáp án
Đổi 8 dm = 0,8 m
Chiều rộng căn phòng là:
12 : 3 = 4 (m)
Diện tích căn phòng là:
12 . 4 = 48 (m2).
Diện tích 1 viên gạch men là:
0,8 . 0,8 = 0,64 (m2).
Số viên gạch men được lát là:
48 : 0,64 = 75 (viên).
Đáp số: 75 viên.
Câu 9:
Tìm x biết x chia hết cho 18, 20, 30 và 200 < x < 400.
 Xem đáp án
Xem đáp án
Vì x chia hết cho 18, 20, 30 nên x thuộc BCNN (18,20, 30 )
Ta có 18 = 2.32
20 = 22 .5
30 = 2.3.5
Vậy BCNN (18, 20, 30) = 22 . 32 . 5 = 180
Vì 200 < x < 400 nên x = 360
Vậy x = 360.
Câu 10:
Một mảnh vườn hình chữ nhật được vẽ trên bản đồ tỉ lệ 1 : 500 có chiều dài là 8 cm, chiều rộng 6 cm . Diện tích của mảnh vườn là bao nhiêu theo đơn vị ha ?
 Xem đáp án
Xem đáp án
Chiều dài thực tế của mảnh vường là:
8 . 500 = 4000(cm).
Chiều rộng thực tế của mảnh vường là:
6 . 500 = 3000 (cm)
Diện tích của mảnh vườn là:
4000 . 3000 = 12000000 (cm2)
Đổi 12000000 cm2 = 1200ha.
Đáp số: 1200 ha.
Câu 11:
Tìm một số có 2 chữ số, biết rằng số đó gấp 5 lần tổng các số của nó.
 Xem đáp án
Xem đáp án
Gọi số tự nhiên có hai chữ số cần tìm là (a khác 0; a, b < 10)
Ta có:
= (a+b) . 5
⇔ 10a + b = 5a + 5b
⇔ 5a = 4b
Vì 5a chia hết cho 5 nên 4b chia hết cho 5 mà 4 không chia hết cho 5. Suy ra: b chia hết cho 5.
Mà a khác 0 nên b = 5.
Suy ra: a = 4
Vậy số cần tìm là 45.
Câu 12:
Tìm một số có 2 chữ số, biết rằng số đó gấp 5 lần tổng các số của nó.
 Xem đáp án
Xem đáp án
Gọi số tự nhiên có hai chữ số cần tìm là (a khác 0; a, b < 10)
Ta có:
= (a+b) . 5
⇔ 10a + b = 5a + 5b
⇔ 5a = 4b
Vì 5a chia hết cho 5 nên 4b chia hết cho 5 mà 4 không chia hết cho 5. Suy ra: b chia hết cho 5.
Mà a khác 0 nên b = 5.
Suy ra: a = 4
Vậy số cần tìm là 45.
Câu 13:
Chứng tỏ rằng với mọi số tự nhiên n thì tích (n + 3)(n + 6) chia hết cho 2.
 Xem đáp án
Xem đáp án
– Nếu n ⋮ 2 thì n = 2k (k ∈ ℕ)
Suy ra : n + 6 = 2k + 6 = 2(k + 3)
Vì 2(k + 3) ⋮ 2 nên (n + 3).(n + 6) ⋮ 2
– Nếu n không chia hết cho 2 thì n = 2k + 1 (k ∈ ℕ)
Suy ra: n + 3 = 2k + 1 + 3 = 2k + 4 = 2(k + 2)
Vì 2(k + 2) ⋮ 2 nên (n + 3).(n + 6) ⋮ 2
Vậy (n + 3).(n + 6) chia hết cho 2 với mọi số tự nhiên n.
Câu 14:
 Xem đáp án
Xem đáp án
A = (x + 2)(x + 3)(x + 4)(x + 5) – 24
A = (x + 2)(x + 5)(x + 3)(x + 4) – 24
A = (x2 + 7x + 10)( x2 + 7x + 12) – 24
Đặt t = x2 + 7x + 11
Khi đó:
A = (t – 1)(t+1) – 24 = t2 – 25 = (t – 5)(t + 5)
A = (x2 + 7x + 6)( x2 + 7x + 16).
Câu 15:
Một đội công nhân có 63 người nhận sửa xong một quãng đường trong 11 ngày. Hỏi muốn làm xong quãng đường đó trong 7 ngày thì cần thêm bao nhiêu người nữa?
 Xem đáp án
Xem đáp án
Một người sửa hết quãng đường đó trong số ngày là:
63 . 11 = 693 (ngày).
Muốn sửa quãng đường đó trong 77 ngày thì cần số người là:
693 : 7 = 99 (người).
Muốn sửa quãng đường đó trong 77 ngày thì cần thêm số người là:
99 – 63 = 36 (người).
Đáp số: 36 người.
Câu 16:
Ngày 28 tháng 3 là thứ năm. Hỏi ngày 23 tháng 8 cùng năm là thứ mấy?
 Xem đáp án
Xem đáp án
Từ ngày 28 tháng 3 đến ngày 23 tháng 8 có số ngày là:
31 + 30 + 31 + 30 + 31 – 5 = 148 (ngày).
Ta thấy: 148 : 7 = 21 (dư 1).
Vậy ngày 23 tháng 8 cùng năm là thứ sáu.
Câu 17:
Mệnh đề sau đúng hay sai: 40009 m2 = 4.
 Xem đáp án
Xem đáp án
Vì 1 ha = 10000 m2
Nên mệnh đề trên là đúng.
Câu 18:
Cho tập A = {0; 1; ....; 9}. Có bao nhiêu cách chọn tập con của A có 6 chữ số trong đó có ít nhất 3 chữ số nhỏ hơn 6.
 Xem đáp án
Xem đáp án
Có cách chọn 3 phần tử nhỏ hơn 6.
Có cách chọn 3 phần tử còn lại.
Vậy có: . = 700 cách chọn tập con thỏa mãn yêu cầu bài toán.
Câu 19:
Tìm số có 3 chữ số . Biết chữ số hàng trăm và chữ số hàng đơn vị giống nhau.nếu nhân số đó với 6 thì được tích số cũng là số có 3 chữ số và trong tích đó có một chữ là 2.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là ( vì số hàng trăm và chữ số hàng đơn vị giống nhau ) nên:
Ta có : . 6 = 6 . ( 100a + 10b + a ) = 6 . ( 101a + 10b ) = 606a + 60b
Mà ta có tích là số có 3 chữ số nên a = 1
Suy ra 606 + 60b có 1 chữ số 2 trong đó nên b = 2.
Vậy số cần tìm là 121.
Câu 20:
Tìm đa thức với hệ số nguyên nhận x = làm nghiệm.
 Xem đáp án
Xem đáp án
Theo bài ra ta có:
x =
⇔
⇔
⇔
⇔ x3 + 6x – 3 =
Bình phương 2 vế, sau đó rút gọn ta được: x6 – 6x4 – 6x3 + 12x2 – 36x + 1 = 0.
Câu 21:
 Xem đáp án
Xem đáp án
Để chia hết cho 5 thì b = 0 hoặc b = 5
Mà chia hết cho 2 nên b chẵn. Vậy b = 0.
Vì chia hết cho 9 nên (a + 4 + 6 + b) chia hết cho 9 hay (a + 10) chia hết cho 9.
Suy ra: a = 8
Vậy a = 8 và b = 0.
Câu 22:
Hai tấm vải dài bằng nhau người ta đã bán đi tấm vải thứ nhất và tấm vải thứ hai biết số mét vải còn lại ở tấm thứ nhất nhiều hơn số mét vải còn lại ở tấm thứ hai là 6m. Hỏi mỗi tấm vải lúc đầu dài bao nhiêu mét?
 Xem đáp án
Xem đáp án
Sau khi bán thì tấm vải thứ nhất còn:
1 − = (chiều dài ban đầu).
Sau khi bán thì tấm vải thứ hai còn:
1 − = (chiều dài ban đầu).
Số mét vải còn lại của tấm thứ nhất nhiều hơn số mét vải còn lại của tấm hai là:
− = (chiều dài ban đầu).
Vậy chiều dài tấm vải ban đầu tương ứng với 6 m.
Vậy chiều dài ban đầu của hai tấm vải là :
6 : = 60 (m).
Đáp số: 60 m.
Câu 23:
Số thập phân gồm mười đơn vị, bốn phần mười, sáu phần nghìn viết là?
 Xem đáp án
Xem đáp án
Số thập phân gồm mười đơn vị, bốn phần mười, sáu phần nghìn viết là: 10,406.
Câu 24:
Cho x, y dương thỏa mãn x + y = 3. Tìm giá trị nhỏ nhất của biểu thức P = .
 Xem đáp án
Xem đáp án
Ta có: P =
⇔ P =
⇔ P
Vậy giá trị nhỏ nhất của P là khi x = y = .
Câu 29:
Tính nhanh: 4982 + 996.502 + 5022.
 Xem đáp án
Xem đáp án
4982 + 996.502 + 5022
= 4982 + 2.498.502 + 5022
= (498 + 502)2
= 10002
= 1 000 000.
Câu 30:
5 xe ô tô thì chở được 25 tấn hàng. Hỏi:
a) 15 xe ô tô nhu thế chở được bao nhiêu tấn hàng?
b) Muốn chở 40 tấn hàng thì cần bao nhiêu xe ô tô như thế?
 Xem đáp án
Xem đáp án
a) 15 ô tô như thế chở được số tấn hàng là:
25 : 5 . 15 = 75 (tấn).
b) Muốn chở 40 tấn hàng thì cần số xe ô tô như thế là:
40 : (25 : 5) = 8 (xe).
Đáp số: a) 75 tấn, b) 8 xe.
Câu 31:
Cho a + 1 và 2a + 1 là các số chính phương. Chứng minh a chia hết cho 24.
 Xem đáp án
Xem đáp án
Đặt a + 1 = x2; 2a + 1 = y2;
a phải chẵn vì 2a = y2 – 1 = (y – 1)(y + 1) suy ra 2a chia hết cho 8 vì y – 1 và y + 1 là tích của 2 số chẵn liên tiếp
Vậy a chia hết cho 2. (1)
a = (x – 1)(x + 1) vì a là số chẵn nên suy ra a chia hết cho 8 do x – 1 và x + 1 là tích của 2 số chẵn liên tiếp (2)
Ta cần chứng minh x không chia hết cho 3.
Giả sử x chia hết cho 3 ⇒ x = 3k
2(a + 1) –1 = 2(x – 1)(x + 1) –1 = 2(9k2 – 1) – 1 = 18k2 – 3
⇒ 2a + 1 chia hết cho 3 vô lý vì ta có 2(a + 1) chia hết cho 3 nhưng – 1 không chia hết cho 3 ⇒ x không chia hết cho 3 hay hoặc x – 1, hoặc x + 1 chia hết cho 3.
Vậy x chia 3 dư 1 hoặc x chia 3 dư 2 mà x là số chính phương nên x chia 3 dư 1.
Khi đó: a = x2 – 1 chia hết cho 3 hay a chia hết cho 3 (3)
Từ (1), (2) và (3) suy ra: a chia hết cho 24.
Câu 32:
Cho tam giác ABC. Gọi D, E theo thứ tự là trung điểm AB, AC. Chứng minh:
a) Xác định dạng tứ giác BDEC.
 Xem đáp án
Xem đáp án
a)
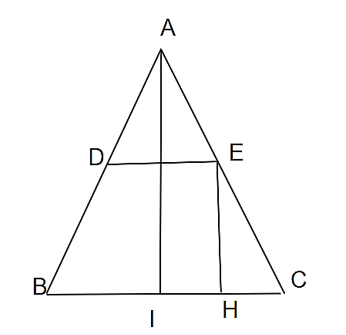
Ta có: AB = AC
D là trung điểm AB và E là trung điểm AC nên DB = EC = (1)
Lại có: DE là đường trung bình của tam giác ABC nên DE // BC (2)
Từ (1) và (2) suy ra: DECB là hình thang cân.
Câu 33:
b) Kẻ DK vuông góc BC, EH vuông góc BC và BC = 8 cm. Tính HC và HB.
 Xem đáp án
Xem đáp án
b) Gọi I là trung điểm BC
Xét tam giác AIC và tam giác EHC có:
Chung
= 90°
⇒ ∆ AIC ᔕ ∆EHC (g.g)
⇒
⇒ CH = 4 : 2 = 2 (cm)
BH = BC – CH = 8 – 2 = 6 (cm).
Câu 34:
 Xem đáp án
Xem đáp án
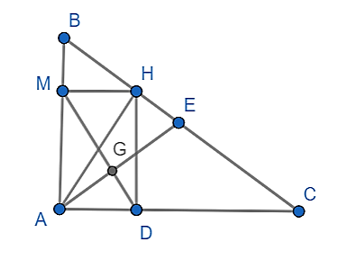
Xét tam giác ABC vuông tại A có AE là trung tuyến
⇒ AE = EC = BE = ( tính chất trung tuyến ứng với cạnh huyền bằng cạnh huyền)
Suy ra: tam giác AEC cân tại E và
Mà (cùng phụ với )
Nên: = (1)
Xét tứ giác AMHD có:
= 90°
= 90°
Suy ra: AMHD là hình chữ nhật.
Suy ra: (2)
Từ (1) và (2) suy ra: =
Lại có: + = 90°
Nên: + = 90°
Suy ra: = 90° hay MD vuông góc với AE.
Vậy MD vuông góc với AE.
Câu 35:
Cho tam giác ABC vuông tại A, gọi I là giao điểm các đường phân giác các góc trong của tam giác ABC, M là trung điểm BC.
a) Biết AB = 6 cm, AC = 8 cm. Tính .
 Xem đáp án
Xem đáp án
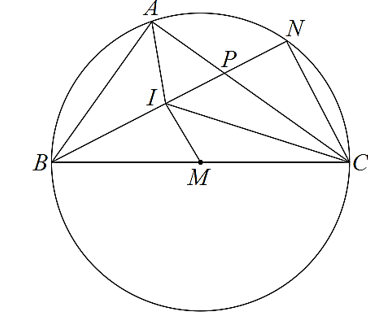
a) Ta có:
BC =
BP =
Ta thấy:
Xét tam giác BAP và tam giác BIM có:
⇒∆BAP ᔕ ∆BIM (c.g.c)
Suy ra: = = 90°
Câu 36:
b) Biết = 90°. Ba cạnh của tam giác ABC tỉ lệ với ba số nào?
 Xem đáp án
Xem đáp án
b) vẽ đường tròn tâm M đường kính BC, BI cắt (M) tại N.
Ta thấy: = 90° suy ra MI // CN
Vì M là trung điểm BC nên I là trung điểm BN (1)
Dễ thấy:
Suy ra: tam giác NIC cân tại N hay NI = NC (2)
Từ (1) và (2) suy ra:
Suy ra:
⇒
Vậy AB : AC : BC = 3 : 4 : 5.
Câu 37:
Giải bài toán dân gian sau:
Em đi chợ phiên
Anh gửi một tiền
Cam, thanh yên, quýt
Không nhiều thì ít
Mua đủ một trăm
Cam ba đồng một
Quýt một đồng năm
Thanh yên tươi tốt
Năm đồng một trái.
Hỏi mỗi thứ mua bao nhiêu trái, biết một tiền bằng 60 đồng?
 Xem đáp án
Xem đáp án
Gọi số cam, quýt, thanh yên đã mua lần lượt là x, y, z (quả) (x, y, z ∈ ℕ*).
Theo đề bài, ta có hệ phương trình:
⇔
⇔
⇔
⇔
⇔ (*)
Vì x > 0 nên 100 – 12z > 0 suy ra: z < hay z ∈ {1; 2;…; 8}
Thay lần lượt các giá trị của z vào (*) ta thấy chỉ có z = 6 thỏa mãn
Vậy z = 6; y = 90 và x = 4.
Vậy số cam, quýt, thanh yên đã mua lần lượt là 4, 90 và 6 quả.
Câu 38:
Một nửa chai chứa nước cân nặng kg. Chai không chứa nước cân nặng kg. hỏi chai đó chứa đầy nước thì cân nặng bao nhiêu ki–lô–gam?
 Xem đáp án
Xem đáp án
1 nửa số nước trong chai cân nặng là:
– = (kg)
Khi chai đầy nước thì số nước này nặng là:
(kg)
Chai đó đầy nước thì cân nặng là:
(kg).
Đáp số: 1 kg.
Câu 39:
Trong một lớp học có ít nhất bao nhiêu sinh viên để có ít nhất 19 sinh viên có cùng tháng sinh?
 Xem đáp án
Xem đáp án
Trong trường hợp tồi nhất thì ứng với mỗi tháng sinh có 18 sinh viên.
Để có ít nhất 19 sinh viên cùng tháng sinh thì cần:
18 . 12 + 1 = 217 (sinh viên).
Vậy cần ít nhất 217 sinh viên.
Câu 40:
Tính B = 1.22 + 2.32 + … + 99.1002.
 Xem đáp án
Xem đáp án
B = 1.22 + 2.32 + … + 99.1002
B = 1.2.2 + 2.3.3 + … + 99.100.100
B = 1.2.(3–1) + 2.3.(4–1) + …. + 99.100.(101 – 1)
B = 1.2.3 – 1.2 + 2.3.4 – 1.2.3 + … + 99.100.101 – 99.100
B = (1.2.3 + 2.3.4 + … + 99.100.101) – (1.2 + 2.3 + … + 99.100)
B = A – C
+ Xét A = 1.2.3 + 2.3.4 + … + 99.100.101
4A = 1.2.3.4 + 2.3.4.(5–1) + ... + 99.100.101.(102–98)
4A = 1.2.3.4 + 2.3.4.5 – 1.2.3.4 + ... + 99.100.101.102 – 98.99.100.101
4A = 99.100.101.102
A = 25497450
+ Xét C = 1.2 + 2.3 + … + 99.100
3C = 1.2.3 + 2.3.3 + ….+ 99.100.3
3C = 1.2.3 + 2.3.(4–1) + … +99.100.(101–98)
3C = 99.100.101
C = 333300
Suy ra: B = A – C = 25497450 – 333300 = 25164150.
Câu 41:
Tính chu vi của hai đường tròn biết tổng chu vi hai đường tròn bằng 75,36 m và bán kính đường tròn thứ nhất gấp ba lần bán kính đường tròn thứ hai.
 Xem đáp án
Xem đáp án
Tổng bán kính hai đường tròn là:
75,36 : 3,14 : 2 = 12 (m).
Bán kình đường tròn thứ hai là:
12 : 4 = 3 (m)
Chu vi đường tròn thứ hai là:
2 . 3 . 3,14 = 18,84 (m)
Chu vi đường tròn thứ nhất là:
75,36 – 18,84 = 56,52 (m)
Câu 42:
 Xem đáp án
Xem đáp án
Để căn thức có nghĩa thì x – 2 ≥ 0 hay x ≥ 2.
Câu 43:
Tìm tất cả số tự nhiên n sao cho: 4n + 9 chia hết cho 2n + 1.
 Xem đáp án
Xem đáp án
Theo bài ra ta có:
4n + 9 ⋮ 2n + 1
⇔ 4n + 2 + 7 ⋮ 2n + 1
⇔ 2(2n + 1) +7 ⋮ 2n + 1
⇒ 7 ⋮ 2n + 1
Suy ra: 2n + 1 ∈ Ư(7) = {1; 7}
Vậy n ∈ {0; 3}.
Câu 44:
Cho hình vuông ABCD. Qua A vẽ 2 đường thẳng vuông góc với nhau, cắt BC tại Q và R, cắt CD tại P và S.
a) Tam giác AQR và APS là tam giác cân.
 Xem đáp án
Xem đáp án
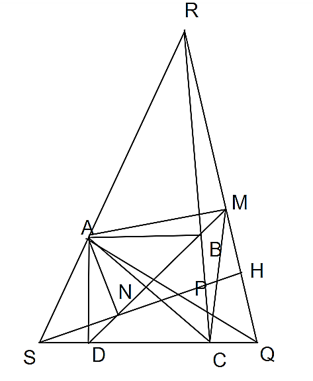
a) Xét tam giác vuông ABR và ADQ có:
AB = AD (giả thiết)
= 90°
Góc = 90°
⇒
⇒ ∆ABR = ∆ADQ (cạnh góc vuông – góc nhọn kề)
⇒ AR = AQ (2 cạnh tương ứng)
⇒ Tam giác AQR cân tại A.
Chứng minh tương tự: ta có ∆ADS = ∆ABP
⇒ AS = AP ⇒ ∆APS cân tại A.
Câu 45:
b) QR cắt PS tại H. M, N là trung điểm của QR và PS. Chứng minh: AMHN là hình chữ nhật.
 Xem đáp án
Xem đáp án
b) ∆AQR cân tại A ⇒ Trung tuyến AM đồng thời là đường cao.
⇒ AM vuông góc với QR ⇒ = 90°
Tương tự: ∆APS cân tại A ⇒ Trung tuyến AN đồng thời là đường cao.
⇒ AN vuông góc với SP ⇒ = 90° hay = 90°.
∆AQR vuông cân tại A ⇒ = 45° ⇒ = 45°.
∆APS vuông cân tại A ⇒ = 45° ⇒ = 45° (đối đỉnh).
Xét ∆PHQ có: + = 45° + 45° = 90°
⇒ ∆PHQ vuông cân tại H ⇒ PH vuông góc với PQ
⇒ = 90°
Xét tứ giác AMHN có: = = = 90°
⇒ AMHN là hình chữ nhật.
Câu 46:
c) P là trực tâm của tam giác SQR.
 Xem đáp án
Xem đáp án
c) Xét ∆SQR có:
BC vuông góc CD ⇒ RC vuông góc SQ ⇒ RC là đường cao.
AP vuông góc AR ⇒ QA vuông góc RS ⇒ QA là đường cao.
Mà RC cắt QA tại P
Vậy P là trực tâm tam giác SQR.
Câu 47:
d) MN là trung trực của AC.
 Xem đáp án
Xem đáp án
d) ∆ANP vuông tại A có trung tuyến AN ⇒ AN =
∆CSP vuông tại C có trung tuyến CN ⇒ CN =
⇒ AN = CN ⇒ N thuộc trung trực của AC.
Tương tự ta có: MA = MC ⇒ M thuộc trung trực của AC.
Vậy MN là trung trực của AC.
Câu 48:
e) M, B, N, D thẳng hàng.
 Xem đáp án
Xem đáp án
e) Ta có BA = BC (giả thiết) ⇒ B thuộc trung trực của AC.
Mà MN là trung trực của AC (chứng minh trên) ⇒ B thuộc MN
Tương tự DA = DC (giả thiết) ⇒ D thuộc trung trực của AC.
Mà MN là trung trực của AC (chứng minh trên) ⇒ D thuộc MN
Vậy M, B, N, D thẳng hàng.
Câu 49:
 Xem đáp án
Xem đáp án
Gọi số cần tìm có dạng:
+ Trường hợp 1
Cách chọn vị trí cho số 0 và 1:
Cách chọn vị trí cho 4 số còn lại:
Suy ra số cách chọn là: .
+ Trường hợp 2:
Số chữ số có số 0 đứng đầu là:
- Cách chọn vị trí cho số 1: 5 cách
- Cách chọn vị trí cho 4 số còn lại:
Vậy có: 5 .
Vậy số chữ số có 6 chữ số khác nhau mà có mặt chữ số 0 và chữ số 1 là:
. – 5 . = 42000 (số).
Câu 50:
Tìm một số có hai chữ số , biết rằng nếu thêm chữ số 0 vào giữa hai số đó thì được một số mới gấp 9 lần số đã cho.
 Xem đáp án
Xem đáp án
Gọi số tự nhiên có hai chữ số cần tìm là (a khác 0; a, b < 10)
Ta có:
= 9 .
⇔ 100a + b = 90a + 9b
⇔ 10a = 8b
⇔ 5a = 4b
Vì 5a chia hết cho 5 nên 4b chia hết cho 5 mà 4 không chia hết cho 5. Suy ra: b chia hết cho 5.
Mà a khác 0 nên b = 5.
Suy ra: a = 4
Vậy số cần tìm là 45.
Câu 51:
 Xem đáp án
Xem đáp án
Ta có:
x2 + 5y2 + 2x – 4xy – 10y + 14
= [x2 + 2x(1 – 2y) + (4y2 – 4y + 1)] + (y2 – 6y + 9) + 4
= (x + 1 – 2y)2 + (y – 3)2 + 4
Ta thấy: (x + 1 – 2y)2 + (y – 3)2 ≥ 0 với mọi x, y
Nên (x + 1 – 2y)2 + (y – 3)2 + 4 ≥ 4 > 0 với mọi x, y.
Vậy x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
Câu 52:
Nêu định nghĩa vectơ chỉ phương và vectơ pháp tuyến.
 Xem đáp án
Xem đáp án
Vectơ được gọi là vectơ chỉ phương của đường thẳng ∆ nếu và giá của song song hoặc trùng với ∆.
Vectơ được gọi là vectơ pháp tuyến của đường thẳng ∆ nếu và vuông góc với vectơ chỉ phương của ∆.
Câu 53:
Chứng minh rằng x2 + xy + y2 + 1 > 0 với mọi x, y.
 Xem đáp án
Xem đáp án
Ta có:
x2 + xy + y2 + 1
=
=
Ta thấy: ≥ 0 với mọi x, y
Nên ≥ 1 > 0 với mọi x, y
Vậy x2 + xy + y2 + 1 > 0 với mọi x, y.
