Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 15)
-
2069 lượt thi
-
186 câu hỏi
-
180 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Ta có:
a3 + b3 + c3 = 3abc
⇔ (a + b)3 – 3ab(a + b) + c3 – abc = 0
⇔ (a + b + c)[(a + b)2 + (a + b)c + c2] – 3ab(a + b + c) = 0
⇔ (a + b + c) [(a + b)2 + (a + b)c + c2 – 3abc] = 0
Do (a + b)2 + (a + b)c + c2 – 3abc > 0 nên a + b + c = 0
Suy ra:
B =
Vậy B = – 1.
Câu 2:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh , SA vuông góc mặt phẳng đáy và SA = (minh họa hình bên). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng?
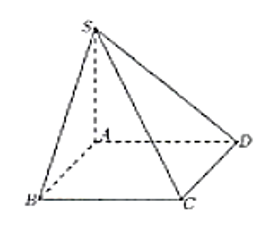
 Xem đáp án
Xem đáp án
Ta có:
SA ⊥ (ABCD) và A ∈ (ABCD) nên A là hình chiếu vuông góc của S trên (ABCD)
Suy ra: AC là hình chiếu vuông góc của SC trên (ABCD).
Khi đó:
Xét tam giác SAC vuông tại A có:
Suy ra: = 30°.
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy và SB = . Tính thể tích khối chóp S.ABCD?
 Xem đáp án
Xem đáp án
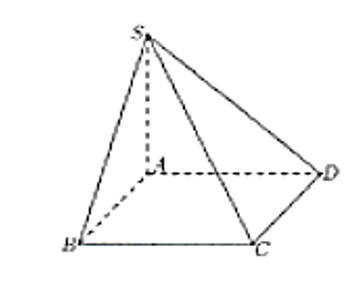
Ta có: SA =
Thể tích khối chóp VS.ABCD = .
Câu 4:
Cho tam giác ABC vuông tại A, biết AC = 5 cm, AB = 6 cm và = 45°. Tính các góc , và cạnh BC (sử dụng định lí côsin)?
 Xem đáp án
Xem đáp án
Vì tam giác ABC vuông tại A nên = 90°
= 180° – 90° – 45° = 45°
Theo định lí côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos
BC2 = 52 + 62 – 2.5.6.cos90°
BC = (cm).
Câu 5:
Nhà bếp dự trữ đủ lượng gạo cho 45 người ăn trong 6 ngày. Nếu có 54 người ăn số gạo đó thì số ngày ăn sẽ giảm đi bao nhiêu ngày (biết rằng suất ăn của mỗi người là như nhau).
 Xem đáp án
Xem đáp án
1 người ăn số gạo đó trong số ngày là:
45 . 6 = 270 ( ngày).
54 người ăn thì số gạo đó ăn trong số ngày là:
270 : 54 = 5 (ngày).
Số ngày giảm đi khi có 54 người ăn là:
6 – 5 = 1 ( ngày).
Đáp số: 1 ngày.
Câu 6:
Tìm a, b, c thỏa mãn a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0.
 Xem đáp án
Xem đáp án
a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0
⇔ (a2 – 2a + 1) + (b2 + 4b + 4) + (4c2 – 4c + 1) = 0
⇔ (a – 1)2 + (b + 2)2 + (2c – 1)2 = 0
Ta thấy: (a – 1)2 + (b + 2)2 + (2c – 1)2 ≥ 0 với mọi a, b, c
Nên để (a – 1)2 + (b + 2)2 + (2c – 1)2 = 0 thì:
⇔
Vậy a = 1; b = –2 và c = .
Câu 7:
Tìm x biết 2x + 2x+3 = 72.
 Xem đáp án
Xem đáp án
2x + 2x+3 = 72
2x + 2x . 23 = 72
2x ( 1 + 23) = 72
2x = 72 : 9
2x = 8 = 23
Vậy x = 3.
Câu 8:
 Xem đáp án
Xem đáp án
Các số nguyên tố nhỏ hơn 20 là: 2; 3; 5; 7; 11; 13; 17; 19
Vậy có 8 số nguyên tố nhỏ hơn 20.
Câu 10:
Không tính trực tiếp, hãy so sánh 202303 và 303202.
 Xem đáp án
Xem đáp án
Ta có:
202303 = 2023.101 = (2023)101
303202 = 3032.101 = (3032)101
Ta so sánh: 2023 và 3032
2023 = (2.101)3 = 23.1013 = 8.101.1012 = 808.1012
3032 = (3.101)2 = 32.1012 = 9.1012
Suy ra: 2023 > 3032
Vậy 202303 > 303202.
Câu 11:
Cho tam giác ABC vuông tại A, đường cao AH và AM là đường trung tuyến, AH = 2 cm, BH = 1 cm. Tính AB, AC, AM.
 Xem đáp án
Xem đáp án
Áp dụng định lí Pitago trong tam giác vuông ABH ta có:
AB2 = AH2 + HB2 = 22 + 12 = 5 (cm).
AB = (cm).
⇔
⇔ AC = (cm).
BC2 = AB2 + AC2 =5 + 20 = 25
BC = 5 (cm)
Vì AM là trung tuyến trong tam giác ABC vuông nên AM = = = 2,5 (cm).
Câu 12:
 Xem đáp án
Xem đáp án
231 = 230 . 2 = (23)10 . 2 = 810 . 2
321 = (32)10 . 3 = 910 . 3
Ta thấy: 2 < 3 và 810 < 910 nên 231 < 321.
Câu 13:
Cho hai tập khác rỗng: A = (m – 1; 4]; B = (–2; 2m + 2), với m ∈ ℝ. Xác định m để A ∩ B = ∅.
 Xem đáp án
Xem đáp án
Vì tập A khác rỗng nên ta có m – 1 < 4 hay m < 5 (1)
Vì tập B khác rỗng nên ta có –2 < 2m + 2.
⇔ –4 < 2m.
⇔ m > –2 (2)
Từ (1) và (2), ta suy ra tập hợp A và B đều khác rỗng khi và chỉ khi –2 < m < 5 (*).
Để A ∩ B ≠ ∅ thì m – 1 < 2m + 2.
Nghĩa là, m > –3 (**).
Giao (*) và (**) lại với nhau, ta thu được kết quả –2 < m < 5.
Câu 14:
Cho tam giác ABC có ba góc nhọn (AB < AC) , đường cao AH. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC; MN cắt AH tại I.
a) Chứng minh I là trung điểm của AH.
 Xem đáp án
Xem đáp án
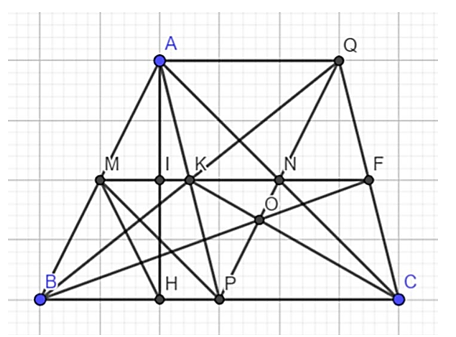
a) Ta có: M, N là trung điểm AB, AC
⇒ MN là đường trung bình ΔABC
⇒ MN // BC ⇒ MI // BH
Mà M, I là trung điểm AB, AH ⇒ MI là đường trung bình ΔABH
Câu 15:
b) Lấy điểm Q đối xứng với P qua N Chứng minh tứ giác ABPQ là hình bình hành.
 Xem đáp án
Xem đáp án
b)Ta có P, Q đối xứng qua N ⇒ N là trung điểm PQ
Mà N là trung điểm AC
AQCP là hình bình hành
⇒ AQ // CP,AQ = CP
Lại có P là trung điểm BC ⇒ BP = PC
⇒ AQ = BP, AQ // BP
⇒ AQPB là hình bình hành.
Câu 16:
c) Xác định dạng của tứ giác MHPN.
 Xem đáp án
Xem đáp án
c) Ta có AQPB là hình bình hành
⇒ AB // PQ ⇒
Mà ΔAHB vuông tại H, M là trung điểm AB
⇒ MH = MA = MB ⇒
⇒ =
⇒
Lại có MN // BC ⇒ MN // HP
⇒ MHPN là hình thang cân.
Câu 17:
d) Gọi K là trung điểm của MN, O là giao điểm của CK và PQ, F là giao điểm của MN và QC. Chứng minh B, O, F thẳng hàng.
 Xem đáp án
Xem đáp án
d) Ta có NP là đường trung bình ΔABC
⇒ NP//AB, NP =
⇒ NP = AM, NP // AM
⇒ AMPN là hình bình hành
⇒ AP ∩ MN tại trung điểm mỗi đường
⇒ K là trung điểm AP
Lại có AQPB là hình bình hành
⇒ AP ∩ BQ tại trung điểm mỗi đường
⇒ K là trung điểm BQ
Vì P là trung điểm BC, CK ∩ QP = O mà O là trọng tâm ΔQBC
Mà MN ∩ QC = {F}
⇒ NF // BC
Vì N là trung điểm QP ⇒ F là trung điểm QC
⇒ B, O, F thẳng hàng.
Vậy B, O, F thẳng hàng.
Câu 18:
Chứng minh rằng: Với bất kỳ bộ 3 số tự nhiên liên tiếp nào thì tích của số thứ nhất và số thứ 3 cùng bé hơn bình phương của số thứ hai 1 đơn vị.
 Xem đáp án
Xem đáp án
Giả sử 3 số tự nhiên liên tiếp là: n – 2; n – 1; n.
Ta có:
n(n – 2) = n2 – 2n
(n – 1)2 = n2 – 2n + 1
Xét: n(n – 2) – (n – 1)2 = n2 – 2n – (n2 – 2n + 1) = –1.
Câu 20:
Lúc 7 giờ sáng Huệ khởi hành từ Hóc Môn đến Củ Chi dự định tới đó lúc 8 giờ 30 phút nhưng đi được quãng đường thì thời giảm vận tốc mất ban đầu. Hỏi Huệ đến nơi lúc mấy giờ?
 Xem đáp án
Xem đáp án
Thời gian đi dự kiến ban đầu là:
8 giờ 30 phút – 7 giờ = 1 giờ 30 phút.
Đổi 1 giờ 30 phút = 90 phút
Thời gian đi hết quãng đường là:
. 90 = 60 phút = 1 giờ.
Thời gian đi hết quãng đường còn lại dự kiến là:
1 giờ 30 phút – 1 giờ = 30 phút
Vận tốc lúc sau giảm còn vận tốc ban đầu nên thời gian đi quãng đường thực tế gấp 4 lần thời gian đi quãng đường dự kiến.
Thời gian đi quãng đường là:
30 . 4 = 120 (phút) = 2 giờ.
Vậy Huệ đến Củ Chi lúc:
7 giờ + 1 giờ + 2 giờ = 10 giờ.
Câu 21:
Một khu đất hình chữ nhật có chiều dài hơn chiều rộng 35 m. Nếu mỗi chiều tăng thêm 5 m thì diện tích tăng thêm là 1450 m2. Hỏi khu đất đó có diện tích là bao nhiêu hécta?
 Xem đáp án
Xem đáp án

Ta có hình vẽ, diện tích tăng thêm 1450 m2 là diện tích của 3 hình 1, 2 và 3.
Hình 1 là hình chữ nhật có hai cạnh là 5m và chiều rộng.
Hình 2 là hình vuông có cạnh là 5m.
Hình 3 là hình chữ nhật có hai cạnh lần lượt là chiều dài và 5m.
Vậy 5 lần chiều rộng cộng 5 lần chiều dài là:
1450 − 5 . 5 = 1425 (m).
Vậy tổng của chiều rộng cộng chiều dài là:
1425 : 5 = 285 (m).
Ta có sơ đồ như hình vẽ.
Chiều dài của hình chữ nhật là:
(285 + 35) : 2=160 (m).
Chiều rộng của hình chữ nhật là:
160 − 35 = 125 (m).
Khu đất có diện tích là:
160 . 125 = 20000 (m2) = 2 ha.
Đáp số: 2 ha.
Câu 22:
Tổng của số bị trừ, số từ và hiệu là 400. Hiệu lớn hơn bốn lần số trừ là 25. Tìm số bị trừ, hiệu và số trừ?
 Xem đáp án
Xem đáp án
Gọi số bị trừ là a, số trừ là b.
Hiệu là a – b
Ta có:
⇔
⇔
Vậy số bị trừ là 200, số trừ là 35.
Câu 23:
Trong một phép chia hai số tự nhiên, biết thương bằng 3; số dư bằng 7 và biết số bị chia hơn số chia 199 đơn vị . Tìm số bị chia?
 Xem đáp án
Xem đáp án
Gọi số bị chia là a, số chia là b (b khác 0)
Ta có: a : b = 3 (dư 7) hay a = 3b + 7 (1)
a – b = 199 (2)
Thay (1) vào (2) ta được:
3b + 7 – b = 199
2b = 192
b = 96
a = 96.3 + 7 = 295.
Vậy số bị chia là 295.
Câu 24:
 Xem đáp án
Xem đáp án
B = 3 + 32 + … + 3100
3B = 32 + 33 + … + 3101
3B – B = (32 + 33 + … + 3101) – (3 + 32 + … + 3100)
2B = 3101 – 3
Ta thấy: 3101 = 34.25+1 nên 3101 có tận cùng là 3
Suy ra: 3101 – 3 có tận cùng là 0
Vậy B có tận cùng là 5.
Câu 25:
Tính bằng cách thuận tiện nhất: 9,67 . 80 . 1,25.
 Xem đáp án
Xem đáp án
9, 67 . 80 . 1,25
= 9,67 . ( 80 . 1,25)
= 9,67 . 100
= 967.
Câu 26:
 Xem đáp án
Xem đáp án
Vì x và y là 2 số tự nhiên liên tiếp nên y – x = 1.
Mà x < 12,34 < y nên x = 12 và y = 13.
Vậy x = 12 và y = 13.
Câu 27:
Tính tổng S = 1 + 2 + 3 + … + 100.
 Xem đáp án
Xem đáp án
Số số hạng của S là:
(100 – 1) : 1 + 1 = 100
Tổng các số hạng của S là:
(100 + 1) . 100 : 2 = 5050.
Câu 28:
Cho x, y, z > 0 và xyz = 1. Tìm giá trị nhỏ nhất B = .
 Xem đáp án
Xem đáp án
Ta có:
Áp dụng bất đẳng thức Cô – si cho 3 số không âm:
≥ +3 = 6.
Vậy giá trị nhỏ nhất của B là 6 khi x = y = z = 1.
Câu 29:
 Xem đáp án
Xem đáp án
(4n + 7)2 – 49
= (4n + 7)2 – 72
= (4n + 7 – 7)(4n + 7 + 7)
= 4n . (4n + 14)
= 8n . (2n + 7)
Vì 8n chia hết cho 8 với mọi n ∈ ℤ suy ra 8n . (2n + 7) chia hết cho 8 với mọi n ∈ ℤ.
Vậy (4n + 7)2 – 49 chia hết cho 8 với n thuộc ℤ.
Câu 31:
Tìm x biết: . 2x + 4 . 2x = 9 . 25.
 Xem đáp án
Xem đáp án
. 2x + 4 . 2x = 9 . 25
2x = 9 . 32
2x . = 288
2x = 64
2x = 26
Vậy x = 6.
Câu 33:
 Xem đáp án
Xem đáp án
1m = 100 cm hay 1 cm = 0,01 m.
26 m 8cm = 26,08 m.
Câu 34:
Cho các số x, y thỏa mãn đẳng thức: 5x2 + 5y2 + 8xy – 2x + 2y + 2 = 0. Tính giá trị của biểu thức M = (x + y)2019 + (x – 2)2020 + (y + 1)2021.
 Xem đáp án
Xem đáp án
5x2 + 5y2 + 8xy – 2x + 2y + 2 = 0
⇔ (4x2 + 8xy + 4y2) + (x2 – 2x +1) + (y2 + 2y + 1) = 0
⇔ 2(x + y)2 + (x – 1)2 + (y + 1)2 = 0 (*)
Vì 2(x + y)2 + (x – 1)2 + (y + 1)2 ≥ 0 với mọi x, y nên để đẳng thức (*) xảy ra thì:
⇔
Thay x = 1 và y = –1 vào M ta được:
M = (1–1)2019 + (1–2)2020 + (–1 + 1)2021 = 1.
Vậy M = 1.
Câu 35:
Một hình chữ nhật có chiều dài gấp đôi chiều rộng. Tính chu vi hình chữ nhật đó biết diện tích hình chữ nhật bằng 32 cm2.
 Xem đáp án
Xem đáp án
Gọi chiều rộng hình chữ nhật là a
Thì chiều dài hình chữ nhật là 2a
Ta có: 2a . a = 32
a2 = 16
a = 4 (cm)
Vậy chiều rộng hình chữ nhật là 4 cm và chiều dài hình chữ nhật là 8 cm.
Chu vi hình chữ nhật là:
(8 + 4) . 2 = 24 (cm).
Đáp số: 24 cm.
Câu 36:
Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB.
 Xem đáp án
Xem đáp án
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang.
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC.
Suy ra: OI // AC ⇒ OI ⊥ AB.
Vì OC và OD lần lượt là phân giác của và nên OC ⊥ OD (tính chất hai góc kề bù). Suy ra: = 90°
Suy ra: IC = ID = IO = .CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Câu 37:
Cho tam giác ABC có = 90°. Vẽ AH vuông góc với BC; HE vuông góc với AB; HF vuông góc với AC. Trên tia đối của tia EH lấy điểm I sao cho EI = EH, trên tia đối của tia FH lấy điểm K sao cho FK = FH.
a) Chứng minh AI = AH.
 Xem đáp án
Xem đáp án
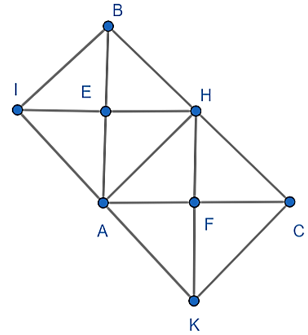
a) Xét ΔAHI có:
AB vừa là đường cao, vừa là trung tuyến nên ΔAHI cân tại A.
⇒ AI = AH và AB là phân giác của (1).
Câu 38:
b) Chứng minh AC là phân giác của .
 Xem đáp án
Xem đáp án
b) Xét ΔAHK có: AC vừa là đường cao, vừa là trung tuyến nên ΔHKA cân tại A.
⇒AH = AK và AC là phân giác của (2)
Câu 39:
c) Chứng minh A là trung điểm của IK. Suy ra BI // CK.
 Xem đáp án
Xem đáp án
c) Từ (1), (2) suy ra = 2 . = 90° . 2 = 180°
⇒ I, A, K thẳng hàng.
Mà AK = AI
Nên A là trung điểm của KI
Xét ΔAHB và ΔAIB có:
AH = AI
BH = BI
AB chung
Do đó: ΔAHB = ΔAIB (c.c.c)
⇒ = 90°
⇒ BI ⊥ IK (3)
Xét ΔAHC và ΔAKC có:
AH = AK
CH = CK
AC chung
Do đó: ΔAHC = ΔAKC (c.c.c)
⇒ = 90°.
⇒ CK ⊥ KI (4)
Từ (3), (4) suy ra BI // CK.
Câu 40:
Giải phương trình nghiệm nguyên: x2y – xy + 2x – 1 = y2 – xy2 – 2y.
 Xem đáp án
Xem đáp án
x2y – xy + 2x – 1 = y2 – xy2 – 2y
⇔ x2y + xy2 – xy – y2 + 2x + 2y = 1
⇔ xy (x + y) – y(x + y) + 2 (x + y) = 1
⇔ (x + y) (xy – y + 2) = 1
Vì x, y nguyên nên:
⇔
⇔
Vậy (x; y) ∈ {(0; 1); (2; –1); (–2; 1); (2; –3)}.
Câu 41:
Khối lớp Bốn mua nhiều hơn khối lớp Ba là 78 tờ báo, nhưng lại mua ít hơn khối lớp Nam là 93 tờ báo. Hỏi trung bình mỗi lớp mua bao nhiêu tờ báo, biết rằng khối lớp Bốn mua 174 tờ báo?
 Xem đáp án
Xem đáp án
Số báo khối lớp Ba mua là:
174 – 78 = 96 (tờ).
Số báo khối lớp Năm mua là:
174 + 93 = 267 (tờ).
Trung bình mỗi lớp mua số báo là:
(174 + 96 + 267) : 3 = 179 (tờ)
Đáp số: Mỗi lớp mua 179 tờ.
Câu 42:
Một công nhân làm việc với mức lương cơ bản là 200000 đồng cho 8 giờ làm việc trong một ngày. Nếu trong một tháng người đó làm 26 ngày và tăng ca thêm 3 giờ/ngày trong 10 ngày thì người đó nhận được bao nhiêu tiền lương? Biết rằng tiền lương tăng ca bằng 150% tiền lương cơ bản.
 Xem đáp án
Xem đáp án
Tiền lương căn bản trong 1 giờ:
200000 : 8 = 25000 (đồng).
Tiền lương tăng ca trong 1 ngày:
(25000 . 3) . 150% = 112500 (đồng).
Tiền lương nhận được trong 1 tháng:
(200000 . 26) + 112500 . 10 = 6325000 (đồng).
Đáp số: 6325000 đồng.
Câu 43:
Một hình chữ nhật có diện tích 486 m2. Tính chu vi hình chữ nhật đó biết tổng chiều dài và chiều rộng gấp 5 lần hiệu của chiều dài và chiều rộng.
 Xem đáp án
Xem đáp án
Gọi chiều dài là a ; chiều rộng là b (m)
Ta có a + b = 5(a – b)
⇔ a + b = 5a – 5b
⇔ 6b = 4a
⇔ 3b = 2a
Lại có ab = 486
⇔ 2ab = 2 . 486
⇔ (3b) . b = 972
⇔ b2 = 324
Suy ra b = 18 vì 182 = 324.
Suy ra a = 486 : 18 = 27
Chu vi hình chữ nhật là:
(27 + 18) . 2 = 90 (m).
Đáp số: 90 m.
Câu 44:
Một hộp đựng khẩu trang bằng bìa cứng có dạng hình hộp chữ nhật. Chiều dài 20cm, chiều rộng 10cm, chiều cao 8cm.
a) Hãy tính thể tích của hộp.
b) Tính diện tích bìa cứng dùng để làm hộp.
 Xem đáp án
Xem đáp án
a) Thể tích của hộp là:
20 . 10 . 8 = 1600 (cm3).
b) Diện tích xung quanh là:
2 . (20 + 10) . 8 = 480 (cm2).
Diện tích 2 đáy là:
20.10.2 = 400 (cm2).
Diện tích bìa cứng để làm hộp là:
480 + 400 = 880 (cm2).
Câu 45:
Một đoàn học sinh đi từ A đến B qua địa điểm C để cắm trại. Sau khi đi đoạn AB mất 2 giờ 30 phút thì họ tăng vận tốc thêm mỗi giờ 1 km để đến C đúng giờ quy định. Tính quãng đường AC, biết rằng đoạn đường AB dài hơn đoạn BC là 0,5 km và đi đoạn đường BC hết 2 giờ.
 Xem đáp án
Xem đáp án
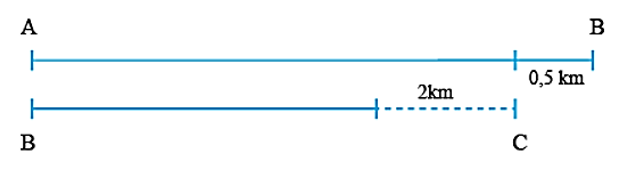
Nếu đi từ B đến C với vận tốc ban đầu thì sau 2 giờ đoàn học sinh mới đến D cách C là 2 km.
Vậy đoạn AB dài hơn đoạn BD là 2,5 km. Suy ra thời gian đi đoạn đường AB nhiều hơn thời gian đi đoạn đường BD (với vận tốc ban đầu) là 30 phút.
Trong 30 phút đi được 2,5 km.
Vậy vận tốc ban đầu là:
2,5 . 2 = 5 (km/giờ).
Quãng đường AB dài:
5 . 2,5 = 12,5 (km).
Quãng đường BC dài là:
12,5 − 0,5 = 12(km).
Quãng đường AC dài là:
12,5 + 12 = 24,5 (km).
Đáp số: 24,5 km.
Câu 46:
Một đội thợ sửa đường ngày đầu sửa được quãng đường và 1 hm. Ngày thứ hai sửa được quãng đường còn lại. Ngày thứ ba sửa được 0,5 km thì vừa xong. Quãng đường lúc đầu dài?
 Xem đáp án
Xem đáp án
Quãng đường thứ nhất được sửa là :
1 hm = 0,1 km
Quãng đường thứ hai được sửa là:
0,1 : 2 = 0,05 (km)
Quãng đường dài số ki–lô–mét là:
0,05 + 0,5 = 0,55 (km)
Vậy quãng đường đó dài 0,55 km.
Câu 47:
Nếu 1 số chia hết cho 45 thì có chia hết cho 3 không?
 Xem đáp án
Xem đáp án
Vì 45 = 9 . 5 = 3 . 3. 5
Vậy 1 số chia hết cho 45 thì chia hết cho 3.
Câu 48:
Tìm một số biết rằng số đó nhân 4 rồi cộng với 18 thì ra là 7742.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là A
Ta có: A . 4 + 18 = 7742
A = (7742 – 18) : 4
A = 1931.
Vậy số cần tìm là 1931.
Câu 49:
Tìm một số có hai chữ số, biết rằng nếu viết thêm chữ số 6 vào bên trái của số đó thì được số mới gấp 9 lần số phải tìm.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là (a ≠ 0; a, b < 10)
Ta có:
= 9 .
⇔ 600 + = 9 .
⇔ 600 = 8 .
⇔ = 600 : 8
⇔ = 75
Vậy số cần tìm là 75.
Câu 50:
Giải phương trình: 2x4 – x3 – 5x2 + x + 2 = 0.
 Xem đáp án
Xem đáp án
2x4 – x3 – 5x2 + x + 2 = 0 (*)
⇔ (2x4 + x3 – 2x2) – (2x3 + x2 – 2x) – (2x2 + x – 2) = 0
⇔ x2 (2x2 + x – 2) – x (2x2 + x – 2) – (2x2 + x – 2) = 0
⇔ (2x2 + x – 2)(x2 – x – 1) = 0
⇔
⇔.
Câu 51:
Tìm x biết: 10 + 2x = 45 : 43.
 Xem đáp án
Xem đáp án
10 + 2x = 45 : 43
10 + 2x = 42 = 16
2x = 6
x = 3.
Vậy x = 3.
Câu 52:
So sánh 230 + 330 + 430 và 3.2410.
 Xem đáp án
Xem đáp án
430 = 230 . 230 = 230 . (22)15 = 230 . 415
3.2410 = 3.310.810 = 311 . (23)10 = 311 . 230
Mà 415 > 311 hay 430 > 311
Vậy 230 + 330 + 430 > 3.2410.
Câu 53:
Cho hình bình hành ABCD có M, N là trung điểm của AB, CD; AN và CM lần lượt cắt BD ở E, F. Chứng minh:
a) Tứ giác AMCN là hình bình hành.
 Xem đáp án
Xem đáp án
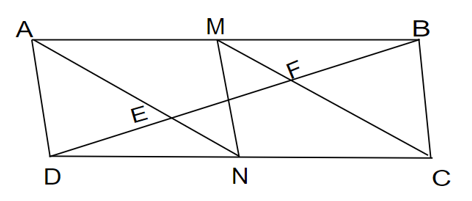
a) Vì tứ giác ABCD là hình bình hành
Suy ra AB // CD, AB = CD.
Vì AB = CD mà M, N lần lượt là trung điểm AB, CD.
Suy ra AM = CN (1).
Mà AM // CN (M, N thuộc AB, CD) (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.
Câu 54:
 Xem đáp án
Xem đáp án
b) Vì AMCN là hình bình hành nên AN//CM.
Xét tam giác ABE có
MF//AE, M là trung điểm AB
⇒ MF là đường trung bình của tam giác
⇒ F là trung điểm BE
Chứng minh tương tự với tam giác CDF, ta được E là trung điểm DF.
⇒ DE = EF = FB.
Vậy DE = EF = FB.
Câu 55:
Một hình chữ nhật có chu vi bằng chu vi hình vuông cạnh 6cm. Chiều dài hơn chiều rộng là 6 cm .Tính diện tích hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Chu vi hình chữ nhật là:
6 . 4 = 24 (cm)
Nửa chu vi hình chữ nhật là:
24 : 2 = 12 (cm).
Chiều rộng hình chữ nhật là:
(12 – 6) : 2 = 3 (cm).
Chiều dài hình chữ nhật là:
3 + 6 = 9 (cm).
Diện tích hình chữ nhật là:
9 . 3 = 27 (cm2).
Đáp số: 27 cm2.
Câu 56:
Lớp 7a cuối năm chỉ có 3 loại học sinh: giỏi, khá, trung bình. Số học sinh trung bình chiếm số học sinh cả lớp. Số học sinh khá bằng 140% số học sinh giỏi. Tính số học sinh mỗi loại biết lớp 7a có 45 em.
 Xem đáp án
Xem đáp án
Số học sinh trung bình là:
45 . = 21 (học sinh).
Tổng số học sinh giỏi và khá là:
45 – 21 = 24 ( học sinh )
Số học sinh khá bằng 140% số học sinh giỏi tức là số học sinh khá bằng lần số học sinh giỏi.
Số học sinh khá là:
24 : ( 14 + 10 ) . 14 = 14 ( học sinh )
Số học sinh giỏi là:
24 – 14 = 10 ( học sinh )
Đáp số : Giỏi : 10 học sinh; Khá : 14 học sinh; Trung bình : 21 học sinh.
Câu 57:
Một miếng bìa hình chữ nhật có chiều dài 18cm và chiều dài gấp đôi chiều rộng. Hỏi diện tích miếng bìa đó bao nhiêu xăng – ti – mét vuông ?
 Xem đáp án
Xem đáp án
Chiều rộng miếng bìa là:
18 : 2 = 9 (cm).
Diện tích miếng bìa là:
18 . 9 = 162 (cm2).
Câu 58:
Tìm số tự nhiên nhỏ nhất sao cho chia 11 dư 6 , chia 4 dư 1, chia 19 dư 11.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là n
Có n : 11 dư 6 ⇒ n – 6 chia hết cho 11 ⇒ n – 6 + 33 = n + 27 chia hết cho 11 (Do 33 chia hết cho 11) (1)
Có n : 4 dư 1 ⇒ n – 1 chia hết cho 4 ⇒ n – 1 + 28 = n + 27 chia hết cho 4 (Do 28 chia hết cho 4) (2)
Có n : 19 dư 11 ⇒ n – 11 chia hết cho 19 ⇒ n – 11 + 38 = n + 27 chia hết cho 19 (Do 38 chia hết cho 19) (3)
Từ (1), (2), (3) ta có:
n + 27 chia hết cho các số 4 ; 11 ; 19 ⇒ n + 27 ∈ BCNN(4 ; 11 ; 19)
Lại có:
4 = 22
11 = 11
19 = 19
BCNN (4; 11; 19) = 22 . 11 . 19 = 836.
Vậy n = 836 – 27 = 809.
Câu 59:
Tỉnh A cách tỉnh B 200 km. Một xe Honda khởi hành từ A đến B,một xe đạp máy đi từ B đến A. Hai xe cùng khởi hành một lúc, đi ngược chiều nhau, gặp nhau cách B 75 km. Nếu xe đạp máy đi trước 1 giờ 12 phút thì họ sẽ gặp nhau ở chỗ cách B 97,5km. Tính vận tốc mỗi xe?
 Xem đáp án
Xem đáp án
Đổi : 1 giờ 12 phút = 1,2 giờ.
1,2 giờ xe đạp máy đi là:
97,5 – 75 = 22,5 (km )
Vận tốc là:
22,5 : 1,2 = 18,75 (km/giờ )
Quãng đường xe Honda đi là:
200 – 75 = 125 (km )
Đi 75 km trong:
75 : 18,75 = 4 (giờ )
Vận tốc xe Honda là:
125 : 4 = 31,25 (km/giờ ).
Câu 60:
Cho 5 số thực không âm a, b, c, d, e có tổng bằng 1. Xếp 5 số này trên một đường tròn. Chứng minh rằng luôn tồn tại một cách xếp sao cho hai số bất kì cạnh nhau có tích không lớn hơn .
 Xem đáp án
Xem đáp án
Gọi 5 số đó là a; b; c; d; e . ta có a+ b + c + d + e = 1
Không mất tính tổng quát, giả sử 0 < a < b < c < d < e
Nhận xét: c + d < . Vì nếu c + d >
Ta có: 2e > c + d > ⇒ e > ⇒ e + c + d > + = 1 .
Mâu thuẫn với a + b + c + d + e = 1 và a, b, c, d, e không âm.
Áp dụng bất đẳng thức Cô si ta có:
Mặt khác:
1 = a + b + c + d + e > a + 3b + e > 3b + e >
Suy ra:
Ta có: ae < be < ; bc < cd < ; da < dc <
Vậy có thể sắp xếp 5 số a, b, c, d, e theo thứ tự như sau: a, e, b, c, d đều thỏa mãn tích 2 số bất kì cạnh nhau không vượt quá .
Câu 61:
 Xem đáp án
Xem đáp án
Tổng mới của hai số là:
46182 + 99 – 145 = 46136.
Đáp số : 46136.
Câu 62:
Viết số thập phân gồm bốn trăm; sáu đơn vị; ba phần mười; hai phần nghìn.
 Xem đáp án
Xem đáp án
Số thập phân là: 406,302.
Câu 63:
Tìm n thuộc ℕ để 3n + 1 chia hết cho 11 – 2n.
 Xem đáp án
Xem đáp án
Ta có: 3n + 1 chia hết cho 11 – 2n
⇒ 2(3n + 1) chia hết cho 11 – 2n
⇒ 6n + 2 chia hết cho 11 – 2n (1)
Mà 3(11 – 2n) chia hết cho 11 – 2n
⇒ 33 – 6n chia hết cho 11 – 2n (2)
Từ (1) và (2) ⇒ 6n + 2 – (33 – 6n) chia hết cho 11 – 2n
Hay 35 chia hết cho 11 – 2n ⇒ 11 – 2n ∈ Ư(35)
⇒ 11 – 2n ∈ {1; 35; 7; 5}
⇒ 2n ∈ {10; 4; 6} (do n là số tự nhiên)
⇒ n ∈ {5; 2; 3}.
Vậy n ∈ {5; 2; 3}.
Câu 64:
Sắp xếp các số sau theo thứ tự từ bé đến lớ: 63817, 6035, 9872, 24655, 63298, 90909.
 Xem đáp án
Xem đáp án
Trong hai số tự nhiên:
– Số nào có nhiều chữ số hơn thì lớn hơn. Số nào có ít chữ số hơn thì bé hơn.
– Nếu hai số có chữ số bằng nhau thì so sánh từng cặp chữ số ở cùng một hàng kể từ trái sang phải.
Vậy sắp xếp đúng là: 6035, 9872, 24655, 63298, 63817, 90909.
Câu 65:
Sắp xếp các số sau theo thứ tự từ bé đến lớn. 42,56; 45,3; 43,13; 42,48; 45,29.
 Xem đáp án
Xem đáp án
Thứ tự sắp xếp đúng là: 42,48; 42,56; 43,13; 45,29; 45,3.
Câu 66:
Cho tam giác ABC có 3 góc nhọn, H là trực tâm, G là trọng tâm. Chứng minh rằng nếu tanB. tanC = 3 thì OH // BC.
 Xem đáp án
Xem đáp án
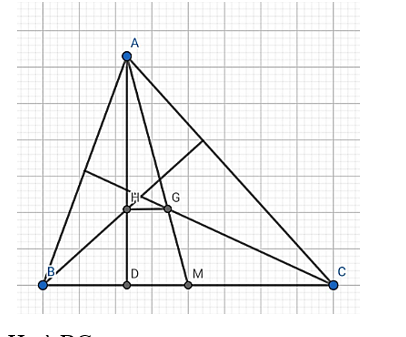
Gọi D là giao điểm của AH và BC
⇒ AD ⊥ BC
M là trung điểm BC nên (1)
Xét ΔADC và ΔBDH có:
= 90°
Do đó ΔADC ᔕ ΔBDH(g.g)
⇒
⇒
⇒ tanB. tanC =
⇒ = 3 (2)
Từ (1) và (2) ⇒ =
⇒ HG // BC (định lý Thales đảo).
Câu 67:
Trong một trận đấu gồm 6 đội bóng thi đấu theo thể thức vòng tròn một lượt. Đội thắng được 3 điểm, hoà được 1 điểm, thua 0 điểm. Kết thúc giải đấu, tổng số điểm của cả 6 đội là 41 điểm.
a) Hỏi giải đấu có bao nhiêu trận?
 Xem đáp án
Xem đáp án
a) Giải đấu có số trận là: =15 trận
Câu 68:
b) Tính số trận hòa của giải đấu?
 Xem đáp án
Xem đáp án
b) Gọi số trận hoà là: x (x ∈ ℕ)
⇒ Số trận không hoà là: 15 – x
Trong trận hoà thì cả hai đội đều tính là hoà nên số điểm của 1 trận hoà là 22 điểm
⇒ Số điểm của các trận hoà là: 2x (điểm)
Trong 1 trận không hoà có 11 độ thắng, 11 đội thua nên số điểm của 1 trận không hoà là 33 điểm
⇒ Số điểm của các trận không hoà là: 3(15 – x) (điểm)
Tổng số điểm là 41 điểm
⇒ 2x + 3(15 – x) = 41
⇔ x = 4
Vậy số trận hoà là 4 trận.
Câu 69:
 Xem đáp án
Xem đáp án
(6x + 1)2 + (6x – 1)2 – 2(1 + 6x)(6x – 1)
= [(6x + 1) – (6x – 1)]2
= (6x + 1 – 6x + 1)2
= 22
= 4.
Câu 70:
An và Bình có tất cả 120 viên bi. Nếu An cho Bình 20 viên bi thì Bình sẽ có ít hơn An là 16 viên bi. Vậy mỗi bạn An, Bình có bao nhiêu viên bi?
 Xem đáp án
Xem đáp án
Theo đề bài ta có sơ đồ:
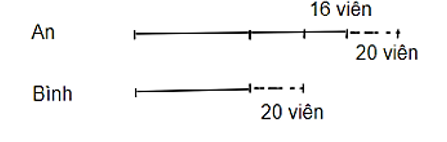
Dựa vào sơ đồ, ta thấy An có nhiều hơn Bình:
20 + 20 + 16 = 56 (viên bi)
Số viên bi An có là:
(120 + 56) : 2 = 88 (viên bi)
Số viên bi Bình có là:
120 – 88 = 32 (viên bi)
Đáp số: An: 88 viên bi
Bình: 32 viên bi
Câu 71:
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng AMCN là hình bình hành.
 Xem đáp án
Xem đáp án
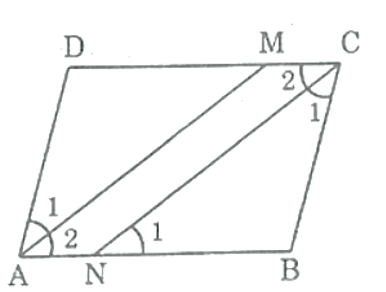
Ta có: (tính chất hình bình hành)
( Vì AM là tia phân giác của )
( Vì CN là tia phân giác của )
Suy ra: =
Do ABCD là hình bình hành nên AB // CD.
Hay AN // CM (1)
Mà = (so le trong)
Suy ra: =
⇒ AM // CN (vì có cặp góc ở vị trí đồng vị bằng nhau) (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.
Câu 72:
Cho p là số nguyên tố lớn hơn 5. Chứng minh rằng tồn tại một số có dạng 111...11 mà chia hết cho p.
 Xem đáp án
Xem đáp án
Gọi số có dạng
an = 11...1 có n chữ số 1
Xét dãy p số a1, a2, a3,.., ap
Nếu tồn tại 1 trong p số trên chia hết cho p thì ta có điều phải chứng minh
Nếu không tồn tại số nào chia hết cho p:
⇒ Khi chia p số trên cho p ta được p – 1 số dư
⇒ Tồn tại ít nhất 2 số có cùng số dư
Giả sử 2 số đó là am, an, m > n
⇒ am−an ⋮ p
⇒ 11...1000...0 ⋮ p có m – n chữ số 1, n chữ số 0
⇒11...1 . 10n ⋮ p
Vì p > 5 ⇒10n không chia hết cho p
⇒ 11...1 ⋮ p.
Câu 73:
Cho tam giác ABC vuông cân ở A, M là một điểm bất kỳ thuộc cạnh huyền BC. Gọi D và E theo thứ tự là hình chiếu của M trên AB và AC.
a) Tứ giác ADME là hình gì?
 Xem đáp án
Xem đáp án
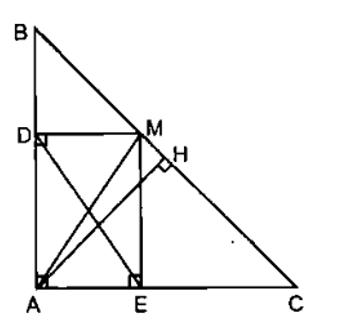
a) Ta có D, E là hình chiếu của M trên AB, AC
Nên DM ⊥ AB và ME ⊥ AC, hay = 90°
Xét tứ giác ADME có = 90°
Suy ra ADME là hình chữ nhật.
Câu 74:
b) Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
 Xem đáp án
Xem đáp án
b) Gọi H là trung điểm BC
Ta có: AH ⊥ BC
ADME là hình chữ nhật nên DE = AM.
Mà AM ≥ AH nên DE ≥ AH
Dấu “=” xảy ra khi M ≡ H
Vậy DE có độ dài nhỏ nhất là AH khi M là trung điểm BC.
Câu 75:
Có hai hộp mỗi hộp chứa 20 quả cầu được đánh số từ 1 đến 20. Chọn ngẫu nhiên mỗi hộp 1 quả cầu. Tính xác xuất để tích số ghi trên hai quả cầu là một số chia hết cho 6.
 Xem đáp án
Xem đáp án
Ta có:
n (Ω) = 20 . 20 = 400
Gọi A là biến cố để tích số ghi trên hai quả cầu là số chia hết cho 6.
+ Trường hợp 1: quả ở hộp 1 chia hết cho 6 hoặc quả hộp 2 chia hết cho 6
Từ 1 đến 20 có 6, 12, 18 chia hết cho 6.
Số cách chọn là: 2. = 120 (cách)
+ Trường hợp 2: quả ở một hộp chia hết cho 3 (nhưng không chia hết cho 2), quả ở hộp còn lại là số chẵn (và không chia hết cho 3).
Từ 1 đến 20 có 3 số không chia hết cho 2 và chia hết cho 3 là: 3; 9; 15.
Từ 1 đến 20 có 7 số chia hết cho 2 và không chia hết cho 3 là: 2; 4; 8; 10; 14; 16; 20.
Số cách chọn là: 3.7.2 = 42 (cách)
n (A) = 120 + 42 = 162
P(A) = .
Câu 76:
Gọi A là tập hợp tất cả các số tự nhiên gồm 4 chữ số phân biệt được chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6. Chọn ngẫu nhiên một số từ tập A, tính xác suất để số được chọn là một số chia hết cho 5.
 Xem đáp án
Xem đáp án
Số phần tử của A là:
6 . = 720.
Số cách chọn 1 số có hàng đơn vị là số 0 có:
= 120 (cách)
Số cách chọn 1 số có hàng đơn vị là số 5 có:
5 . = 100 (cách)
Số cách chọn 1 số chia hết cho 5 là:
120 + 100 = 220 (cách)
Xác suất để số được chọn là một số chia hết cho 5 là:
220 : 720 = .
Câu 77:
Một trường có 126 học sinh nam và cứ 7 học sinh nam có 3 học sinh nữ. Hỏi trường đó có tất cả bao nhiêu học sinh ?
 Xem đáp án
Xem đáp án
Lời giải:
126 học sinh nam có thể chia là số nhóm (mỗi nhóm 7 học sinh) là:
126 : 7 = 18 (nhóm).
Cứ 1 nhóm là có 3 học sinh nữ, cho nên số học sinh nữ là:
18 . 3 = 54 (học sinh).
Vậy trường có tổng số học sinh là:
126 + 54 = 180 (học sinh).
Đáp số: 180 học sinh.
Câu 78:
Nhà bếp của một công ty chuẩn bị gạo cho 65 người, mỗi người 20 kg gạo ăn trong 30 ngày. Hỏi nhà bếp chuẩn bị bao nhiêu tấn gạo?
 Xem đáp án
Xem đáp án
Nhà bếp cần chuẩn bị số kg gạo là:
65 . 20 . 30 = 39000 (kg)
Đổi 39000kg = 39 tấn
Đáp số: 39 tấn gạo.
Câu 79:
Số nghiệm của phương trình: cos 3x = sin x.
 Xem đáp án
Xem đáp án
cos 3x = sin x
⇔ cos 3x – sin x = 0
⇔ cos 3x = sin x = cos
⇔
⇔
Câu 80:
Tìm giá trị nhỏ nhất của biểu thức A = (x – 1)(x + 2)(x + 3)(x + 6) + 2045.
 Xem đáp án
Xem đáp án
A = (x – 1)(x + 2)(x + 3)(x + 6) + 2045
A = (x – 1)(x + 6)(x + 2)(x + 3) + 2045
A = (x2 + 5x – 6)(x2 + 5x + 6) + 2045.
A = (x2 + 5x)2 – 62 + 2045
A = (x2 + 5x)2 + 2009
Vì (x2 + 5x)2 ≥ 0 với mọi x nên A ≥ 2009.
Vậy giá trị nhỏ nhất của A là 2009 khi: x2 + 5x = 0
Suy ra: x = 0 hoặc x = – 5.
Câu 81:
Tìm x, y ∈ ℕ biết: 36 – y2 = 8(x – 2020)2.
 Xem đáp án
Xem đáp án
36 – y2 = 8(x – 2020)2
⇔
Vì x, y ∈ ℕ suy ra: là một số chính phương
Mà y ≥ 0 suy ra: 0 ≤ ≤
Suy ra: ⇔
Với y = 6 thì x = 2020
Với y = 2 thì x = 2022.
Vậy (x; y) ∈ {(2020; 6); (2022; 2)}.
Câu 82:
Cho tam giác nhọn ABC, các đường cao AK, BD và CE cắt nhau ở H. Gọi (O) là đường tròn đường kính AH. M là trung điểm BC.
Chứng minh D và E cùng thuộc đường tròn (O)
 Xem đáp án
Xem đáp án
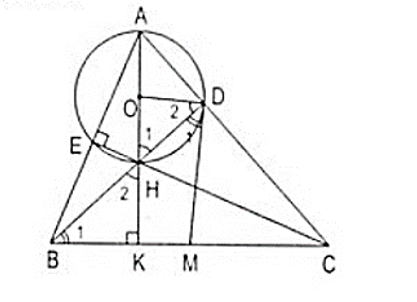
Xét tam giác ADH, tam giác AEH lần lượt vuông tại D, E nên:
= 90° + 90° = 180°
Suy ra tứ giác ADHE nội tiếp đường tròn (O)
Mà AH là đường kính.
Vậy D, E thuộc (O) đường kính AH.
Câu 83:
Số 126 có bao nhiêu ước số tự nhiên?
 Xem đáp án
Xem đáp án
Ta có: 126 = 2 . 32 . 7
Số các ước số của 126 là:
(1 + 1)(2 + 1)(1 + 1) = 2 . 3 . 2 = 12.
Câu 84:
Cho A = 2 + 22 + 23 + … + 260. Chứng minh rằng A chia hết cho 3, 5, 7.
 Xem đáp án
Xem đáp án
A = (2 + 22 ) + (23 +24 ) + ... + (259 + 260 )
A = 2.(1+2) + 23 .(1 + 2) + ... + 259.(1 + 2)
A = 2.3 +23.3 + … + 259 .3
A = 3 . (2 + 23 + ... + 259 )
Vì 3 chia hết cho 3 ⇒ 3 . (2 + 23 + ... + 259 ) chia hết cho 3
⇒ A chia hết cho 3.
A = (2 + 22 + 23 ) +... + (258 + 259 + 260 )
A = 2. (1 + 2 + 22 ) +... + 258 .(1 + 2 + 22 )
A = 2.7 +... +258 .7
A = 7.(2 + ...+ 258 )
Vì 7 chia hết cho 7 ⇒7.(2 + ...+ 258 ) chia hết cho 7
⇒ A chia hết cho 7.
A = (2 + 22 + 23 + 24 )+...+(257 + 258 + 259 + 260 )
A = 2.(1+ 2 + 22 + 23 )+...+ 257.( 1+ 2 + 22 + 23)
A = 2.15 + ... +257 .15
A = 15.(2 + ... +257 )
A = 3.5.(2 + ... +257 )
vì 5 chia hết cho 5 ⇒ 3.5.(2 + ... +257 ) chia hết cho 5
⇒ A chia hết cho 5
Vậy A chia hết cho 3, 5, 7.
Câu 86:
Tính A = (100 – 1) . (100 – 2) . . . . . (100 – 99) . (100 – 100)
 Xem đáp án
Xem đáp án
A = (100 – 1) . (100 – 2) . . . . . (100 – 99) . (100 – 100)
A = 99.98…1.0
A = 0.
Câu 87:
Cho 2 số tự nhiên liên tiếp có tổng là 4025. Tìm 2 số đó.
 Xem đáp án
Xem đáp án
Gọi 2 số tự nhiên liên tiếp là n và n + 1
Ta có:
n + n + 1 = 4025
2n = 4024
n = 2012.
Vậy 2 số tự nhiên liên tiếp cần tìm là 2012 và 2013.
Câu 89:
Cho a + b + c + d = 0. Chứng minh rằng: a3 + b3 + c3 + d3 = 3(ab – cd)(c + d).
 Xem đáp án
Xem đáp án
a + b + c + d = 0
⇔ a + b = – (c + d)
⇔ (a + b)3 = – (c + d)3
⇔ a3 + b3 + 3ab (a + b) = –c3 – d3 – 3cd(c + d)
⇔ a3 + b3 + c3 + d3 = – 3ab(a + b) – 3cd(c + d)
⇔ a3 + b3 + c3 + d3 = 3ab(c + d) – 3cd(c + d)
⇔ a3 + b3 + c3 + d3 = 3(ab – cd)(c + d).
Vậy a3 + b3 + c3 + d3 = 3(ab – cd)(c + d).
Câu 90:
Biết rằng diện tích trồng nhãn của một xã là 6ha. Hỏi diện tích trồng nhãn của xã đó là bao nhiêu mét vuông?
 Xem đáp án
Xem đáp án
Coi 6ha tương ứng bằng 3 đoạn thẳng dài như nhau thì mỗi đoạn thẳng tương ứng:
6 : 3 = 2 (ha)
Diện tích trồng nhãn của xã tương ứng bằng 5 đoạn thẳng và bằng:
2 . 5 = 10 (ha) = 100000 (m2)
Đáp số: 100000 m2.
Câu 91:
4 con bò ăn trong một ngày hết 1 tạ cỏ. Hỏi 2 con bò như thế ăn trong 30 ngày hết bao nhiêu tấn cỏ?
 Xem đáp án
Xem đáp án
Đổi: 1 tạ = 100 kg
1 con bò tiêu thụ số cỏ trong 1 ngày là:
100 : 4 = 25(kg)
2 con bò ăn cỏ trong 30 ngày tương ứng với:
2 . 30 = 60 (con bò)
2 con bò trong 30 ngày tiêu thụ hết số cỏ:
25 . 60 = 1500 (kg)
Đổi: 1500 kg = 1,5 tấn
Câu 92:
Cả hai lớp 4A và 4B trồng được 700 cây. Lớp 4A trồng được ít hơn lớp 4B là 150 cây. Vậy lớp 4A trồng được… cây, lớp 4B trồng được… cây. Số thích hợp lần lượt điền vào chỗ chấm là?
 Xem đáp án
Xem đáp án
Số cây lớp 4A trồng được là:
(700 – 150) : 2 = 275 (cây)
Số cây lớp 4B trồng được là:
(700 + 150) : 2 = 425 (cây)
Đáp số: lớp 4A: 275 cây; lớp 4B: 425 cây.
Câu 93:
Dùng 3 số 5, 1 số 1 tạo ra phép tính có kết quả là 24 ? (có thể dùng số thập phân và phân số)
 Xem đáp án
Xem đáp án
Ta có: 24 = 5! : : 1 = 120 : 5 : 1
Vậy ta có phép tính 5! : : 1 = 24.
Câu 95:
Tính hợp lý nếu có thể: (–23). 63 + 23. 21 – 58. 23.
 Xem đáp án
Xem đáp án
(–23). 63 + 23. 21 – 58. 23
= 23 . (–63 + 21 – 58)
= 23. (–100)
= –2300.
Câu 96:
Nhân dịp đi du lịch về mai mang đến lớp 75 chiếc kẹo và 50 gói bim bim để chia cho các bạn. Sau khi chia hết cho các bạn (tính cả mình) thì Mai còn thừa 3 chiếc kẹo và 2 gói bim bim. Hỏi lớp Mai có bao nhiêu bạn biết số học sinh có nhiều hơn 20.
 Xem đáp án
Xem đáp án
Gọi số học sinh lớp Mai là x
Vì sau khi chia xong còn dư 3 kẹo và 2 bim bim
⇒ 75–3 chia hết cho x; 50 – 2 chia hết cho x
⇒ 72 chia hết cho x; 48 chia hết cho x
Ta có
X ∈ BC{72; 48} (x > 20; x ∈ ℕ}
⇒ x ∈ BC{72; 48} = {1; 2; 3; 4; 6; 8; 12; 16; 24}
⇒ x = 24 (vì 24 thỏa mãn lớn hơn 20)
Vậy lớp Mai có 24 học sinh.
Câu 97:
Một phân xưởng có 24 máy dệt, mỗi ngày dệt được 264 cái áo. Nếu phân xưởng đó có thêm 12 máy nữa thì mỗi ngày dệt được tát cả bao nhiêu cái áo? (Năng suất mỗi máy là như nhau).
 Xem đáp án
Xem đáp án
Số cái áo 1 máy dệt trong 1 ngày là:
264 : 24 = 11 (cái )
Số máy sau khi thêm là:
24 + 12 = 36 (máy)
Số áo mà 36 máy dệt được trong một ngày là
11 . 36 = 396 (cái)
Đáp số: 396 cái áo.
Câu 98:
Viết các số đo khối lượng sau đây theo thứ tự giảm dần: 3 tấn; 4 tấn 5 tạ; 5300 kg
 Xem đáp án
Xem đáp án
Ta có: 3 tấn = 3000kg
4 tấn 5 tạ = 4500kg
Ta thấy 3000kg < 4500kg < 5300kg
⇒ 3tấn < 4 tấn 5 tạ < 5300kg
Vậy khối lượng theo thứ tự giảm dần là:
5300kg; 4 tấn 5 tạ; 3 tấn.
Câu 99:
Cho tam giác ABC có AB = 10cm, AC = 17cm, BC = 21cm và đường cao AH.
a) Tính AH.
 Xem đáp án
Xem đáp án
a) Đặt AH = x
Ta có:
AB2 = AH.BH hay 100 = x.BH ⇒ x = (1)
AC2 = AH.CH hay 289 = x.CH (2)
Thay (1) vào (2) ta có:
289 = .CH
⇔ 6069 – 289CH = 100CH
⇔ CH ≈ 15,6 (cm)
AH = 289 : 25,6 ≈ 18,5 (cm)
Câu 100:
b) Tính các góc của tam giác ABC.
 Xem đáp án
Xem đáp án
b) Xét tam giác ABC có: cos A =
Suy ra: ≈ 99°
Tương tự: cos B =
Suy ra: ≈ 53°
= 180° – 99° – 53° = 28°.
Câu 101:
 Xem đáp án
Xem đáp án
n4 + 64 = (n2 + 8)2 – (4n)2 = (n2 + 8 – 4n)(n2 + 8 + 4n)
Ta thấy: n4 + 64 chia hết cho n2 + 8 – 4n và n2 + 8 + 4n tức n4 + 64 có nhiều hơn 2 ước.
Vậy n4 + 64 là hợp số.
Câu 102:
 Xem đáp án
Xem đáp án
3x2 + 6y2 + 2z2 + 3y2z2 – 18 = 6 (1)
⇔ 3(x – 3)2 + 6y2 + 2z2 + 3y2z2 = 33 (2)
Vì 3(x – 3)2 + 6y2 +3y2z2 chia hết cho 3 và 33 chia hết cho 3.
Suy ra: z2 chia hết cho 3
Mà 2z2 ≤ 33.
Suy ra: ≤ 3.
Vì z nguyên nên z = 0 hoặc = 3.
+ Với z = 0 thì (2) trở thành: (x – 3)2 + 2y2 = 11 (3)
Từ (3) suy ra: 2y2 ≤ 11.
⇒ ≤ 2.
– Nếu y = 0 thì (3) không có số nguyên x nào thỏa mãn
– Nếu = 1 từ (3) suy ra: x ∈ {0; 6}
+ Với = 3 thì (2) trở thành: (x–3)2 + 11y2 = 5 (4)
Từ (4) suy ra: 11y2 ≤ 5.
⇒ y = 0, (4) không có số nguyên x nào thỏa mãn
Vậy (x; y; z) ∈ {(0;1;0); (0;–1;0); (6;1;0); (6;–1;0)}.
Câu 103:
. Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
a) A = {0; 3; 6; 9; 12; 15};
b) B = {5; 10; 15; 20; 25; 30};
 Xem đáp án
Xem đáp án
a) A = {0; 3; 6; 9; 12; 15};
Ta thấy các số 0; 3; 6; 9; 12; 15 là các số tự nhiên chia hết cho 3 và nhỏ hơn 16 nên ta viết tập hợp A bằng cách chỉ ra tính chất đặc trưng là:
A = {x | x là số tự nhiên chia hết cho 3, x < 16}.
b) B = {5; 10; 15; 20; 25; 30};
Ta thấy các số 5; 10; 15; 20; 25; 30 là các số tự nhiên chia hết cho 5, lớn hơn 0 và nhỏ hơn 31 (hoặc ta có thể viết nhỏ hơn 32; …; 35).
Vậy ta có thể viết tập hợp B bằng các cách sau:
Cách 1:
B = {x | x là các số tự nhiên chia hết cho 5, 0 < x < 31}.
Cách 2:
B = {x | x là các số tự nhiên chia hết cho 5, 0 < x < 35}…
Câu 104:
Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
c) C = {10; 20; 30; 40; 50; 60; 70; 80; 90};
d) D = {1; 5; 9; 13; 17}.
 Xem đáp án
Xem đáp án
c) C = {10; 20; 30; 40; 50; 60; 70; 80; 90};
Ta thấy các số 10; 20; 30; 40; 50; 60; 70; 80; 90 là các số tự nhiên chia hết cho 10, lớn hơn 0 và nhỏ hơn 100 (hoặc ta có thể viết nhỏ hơn 91; …; 99).
Vậy ta có thể viết tập hợp C bằng các cách sau:
Cách 1:
C = {x | x là các số tự nhiên chia hết cho 10, 0 < x < 91}.
Cách 2:
C = {x | x là các số tự nhiên chia hết cho 10, 0 < x < 100}…
d) D = {1; 5; 9; 13; 17}
Ta thấy các số 1; 5; 9; 13; 17 là các số tự nhiên thỏa mãn số sau hơn số trước 4 đơn vị (hay còn gọi là hơn kém nhau 4 đơn vị), lớn hơn 0 và nhỏ hơn 18.
Do đó ta viết tập hợp D là:
D = {x | x là các số tự nhiên hơn kém nhau 4 đơn vị, 0 < x < 18}.
Câu 105:
 Xem đáp án
Xem đáp án
Các số tự nhiên có 3 chữ số khác nhau lập được là:
123; 132; 231; 213; 321; 312.
Câu 106:
Cho biết 12 + 22 + 32 + … + 102 = 385. Tính nhanh giá trị của biểu thức sau:
S = (122 + 142 + 162 + 182 + 202) – (12 + 32 + 52 + 72 + 92).
 Xem đáp án
Xem đáp án
Ta có:
12 + 22 + 32 + … + 102 = 385
Suy ra: 12 + 32 + 52 + 72 + 92 = 385 – (22 + 42 + 62 + 82 + 102)
12 + 32 + 52 + 72 + 92 = 385 – 22 (12 + 22 + 32 + 42 + 52)
122 + 142 + 162 + 182 + 202 = 22 (62 + 72 + 82 + 92 + 102)
Suy ra: S = (122 + 142 + 162 + 182 + 202) – (12 + 32 + 52 + 72 + 92)
S = 22 (62 + 72 + 82 + 92 + 102) – 385 + 22 (12 + 22 + 32 + 42 + 52)
S = 22 (12 + 22 + 32 + 42 + 52 + 62 + 72 + 82 + 92 + 102) – 385
S = 4.385 – 385
S = 1155.
Vậy S = 1155.
Câu 107:
 Xem đáp án
Xem đáp án
Theo bài ra ta có:
y = x3 – 6x2 – 1
y' = 3x2 – 12x
Xét y' = 0 ta có:
3x2 – 12x = 0
⇔ x2 – 4x = 0
⇔
Ta có bảng biến thiên:
Ta có bảng biến thiên
|
x |
– ∞ 0 |
4 +∞ |
|
f'(x) |
+ 0 |
– 0 + |
|
f(x) |
–1
–∞ |
+∞
–33 |
Vậy hàm số có 2 điểm cực trị là A (0; –1) và B (4; –33).
Câu 108:
 Xem đáp án
Xem đáp án
Nếu 1 người ăn hết số gạo đó trong số ngày là:
14 . 5 = 70 ( ngày)
Số người sau khi thêm là:
5 + 2 = 7 (người)
7 người ăn số gạo đó trong số ngày là:
70 : 7 = 10 (ngày)
Đáp số: 10 ngày.
Câu 109:
Có bao nhiêu số nguyên dương có ba chữ số mà tích của tất cả các chữ số tạo nên số đó đều bằng 18?
 Xem đáp án
Xem đáp án
Gọi số nguyên dương có 3 chữ số thỏa mãn yêu cầu bài toán là (a ≠ 0; a, b, c < 10)
Ta có: a.b.c = 18
Ta thấy: 18 = 1.3.6 = 1.2.9 = 3.3.2
Vậy lập được các số là: 136; 163; 361; 316; 613; 631; 921; 912; 192; 129; 219; 291; 332; 323; 233.
Vậy có 15 số thỏa mãn yêu cầu bài toán.
Câu 110:
Mẫu số chung nhỏ nhất của là bao nhiêu?
 Xem đáp án
Xem đáp án
Lời giải:
Ta có: 9 = 3.3
30 = 3.10
Vậy mẫu số chung nhỏ nhất là 90.
Câu 111:
Tìm n ∈ ℕ* sao cho n2 – 14n – 256 là số chính phương.
 Xem đáp án
Xem đáp án
Giả sử n2 – 14n – 256 là số chính phương
Suy ra: n2 – 14n – 256 = a2 (a ∈ ℕ*).
⇔ n2 – 7n – 7n + 49 – 305 = a2
⇔ (n – 7)2 – a2 – 305 = 0
⇔ (n – 7 + a)(n – 7 – a) = 305
Vì a, n đều là số tự nhiên nên n – 7 – a < n – 7 + a
Mà 305 = 1.305 = 5.61
+ Nếu n – 7 + a = 305 và n – 7 – a = 1
⇒ n – a = 8; n + a = 312
⇒ n = 160
+ Nếu n – 7 + a = 61 và n – 7 – a = 5
⇒ n – a = 12; n + a = 68
⇒ n = 40.
Vậy n = 40 hoặc n = 160.
Câu 112:
Để viết các số tự nhiên liên tiếp từ 2 đến 125 thì cần dùng bao nhiêu chữ số?
 Xem đáp án
Xem đáp án
Từ 2 đến 9 có số chữ số là:
(9 − 2) : 1 + 1 = 8 (số).
Để viết từ 2 đến 9 cần số chữ số là:
8 . 1 = 8 (chữ số).
Từ 10 đến 99 có số chữ số là:
(99 − 10) : 1 + 1 = 90 (số).
Để viết từ 10 đến 99 cần
Số chữ số là:
90 . 2 = 180 (chữ số).
Từ 100 đến 125 có số chữ số là:
(125 − 100) : 1 + 1 = 26 (số).
Để viết từ 2 đến 9 cần số chữ số là:
26 . 3 = 78 (chữ số).
Câu 113:
Đồng hồ kim chỉ 1 giờ 15 phút tạo góc bao nhiêu độ?
 Xem đáp án
Xem đáp án

Đồng hồ hình tròn có 12 con số ứng với 360 độ.
60 phút thì kim phút sẽ quay được 360 độ nên 1 phút thì kim phút sẽ quay được:
360 : 60 = 6 (độ)
12 giờ, kim giờ sẽ quay được 360 được nên 1 giờ thì kim giờ sẽ quay được:
360 : 12 = 30 (độ)
1 phút kim giờ quay được:
30 : 60 = 0,5 (độ)
Đồng hồ kim chỉ 1 giờ 15 phút tạo góc:
= 52,5 (độ).
Câu 114:
So sánh (–5)39 và (–2)91.
 Xem đáp án
Xem đáp án
Ta có:
(–5)39 = [(–5)3]13 = (–125)13
(–2)91 = [(–2)7]13 = (–128)13
Vì (–125)13 > (–128)13 nên (–5)39 > (–2)91.
Câu 115:
Chứng tỏ rằng hai số 20142013 – 1 và 20142013 + 1 không thể đồng thời là hai số nguyên tố.
 Xem đáp án
Xem đáp án
Ta có:
2014 ≡ 1 (mod 3)
Suy ra: 20142013 ≡ 1 (mod 3) hay 20142013 – 1 chia hết cho 3
Mà 20142013 – 1 > 3 nên 20142013 – 1 là hợp số.
Vậy 20142013 – 1 và 20142013 + 1 không thể đồng thời là hai số nguyên tố.
Câu 116:
Cho tam giác ABC vuông tại C, = 42°; AC = 12 cm; BC = 22 cm. Tính các cạnh và các góc của tam giác ABC.
 Xem đáp án
Xem đáp án
Ta có:
AB2 = AC2 + BC2
AB =
Vì tam giác ABC vuông tại C nên = 90°
= 180° – 90° – 42°= 48°.
Câu 117:
Thực hiện phép tính: 20 – [30 – (5 – 1)2].
 Xem đáp án
Xem đáp án
Lời giải:
20 – [30 – (5 – 1)2]
= 20 – [30 – 16]
= 20 – 14
= 6.
Câu 118:
Thực hiện phép tính: 47 – [(45. 24 – 52 . 12) : 14].
 Xem đáp án
Xem đáp án
47 – [(45. 24 – 52 . 12) : 14]
= 47 – (420 : 14)
= 47 – 30
= 17.
Câu 119:
6 người thợ trong 4 giờ quét vôi được 120 m2. Vậy 8 người thợ quét trong mấy giờ thì được 200 m2. (Mỗi người làm sức như nhau).
 Xem đáp án
Xem đáp án
1 người trong 1 giờ quét được số mét vuông là
120 : 4 : 6 = 5 (m2).
8 người trong 1 giờ quét được số mét vuông là
5 . 8 = 40 (m2).
Để quét được 200 mét vuông cần số giờ là
200 : 40 = 5 (giờ).
Đáp số: 5 giờ.
Câu 121:
Số trung bình cộng của hai số bằng 9. Biết một trong hai số đó bằng 12. Tìm số kia.
 Xem đáp án
Xem đáp án
Tổng của hai số là:
9 × 2 = 18
Số còn lại là:
18 – 12 = 6.
Đáp số: 6.
Câu 122:
 Xem đáp án
Xem đáp án
+ Trường hợp 1: Các số pi đều lớn hơn 2
Do pi nguyên tố nên pi có dạng 4n + 1 hoặc 4n + 3.
⇒ pi2 chia 4 luôn dư 1.
p12 + p22 + p32 + p42 + p52 + p62 + p72 chia 4 dư 3 hay vế trái có dạng 4k + 3
Mà vế phải (*) là p82 có dạng 4t + 1 (vì là số chính phương)
Suy ra: Trường hợp 1 vô nghiệm.
+ Trường hợp 2: có 1 số nguyên tố chẵn (bằng 2), các số còn lại lẻ:
Giả sử số nguyên tố chẵn đó là p12, khi đó vế trái là số chẵn và lớn hơn 2
Vế phải là số chẵn hay p8 = 2 (vô lí)
Vậy trường hợp này loại.
+ Trường hợp 3: có 2 số bằng 2.
Giả sử p1 = p2 = 2.
Khi đó: p12 + p22 = 8 chia hết cho 8
⇒ p32 + p42 + p52 + p62 + p72 chia 8 dư 7
Mà p82 chia 8 dư 1.
Vậy trường hợp 3 vô nghiệm.
+ Trường hợp 4: có 6 số bằng 2, 1 số > 2
Giả sử: p1 = p2 = … = p6 = 2, p7 > 2.
Ta có: 24 + p72 = p82
24 = (p8 – p7)( p8 + p7)
Ta thấy 24 = 3.8 = 12.2 = 1.24 = 4.6
Thử các trường hợp ta được p7 = 5 và p8 = 7 là thỏa mãn.
Vậy các số cần tìm là: 2, 2, 2, 2, 2, 2, 5.
Câu 123:
Cho biết tổng của sáu số là 42, hãy tính trung bình cộng của sáu số đó.
 Xem đáp án
Xem đáp án
Trung bình cộng của sáu số đó là:
42 : 6 = 7.
Đáp số: 7.
Câu 124:
Cho đường tròn tâm O đường kính AB. Vẽ dãy CD đi qua trung điểm I của OA và vuông góc với OA.
a) Tính độ dài dây CD biết AB = 20 cm.
 Xem đáp án
Xem đáp án
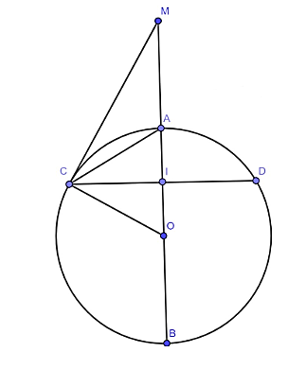
a) Nối O với C.
Có: CO, AO, OB là bán kính; AB là đường kính
⇒ CO = AO = OB = 10 (cm) =
Có: I là trung điểm của OA (giả thiết) nên AI = IO = 5 (cm) = .
Có: CD⊥OA tại I hay OI ⊥ CD tại I nên = 90°.
Xét (O), có:
AO là 1 phần của đường kính
CD là dây cung không đi qua tâm
AO ⊥ CD tại I
⇒ I là trung điểm của CD (Mối quan hệ giữa đường kính và dây)
⇒ CI = ID = ⇔ CD = 2CI = 2ID
Xét ΔOIC vuông tại I có:
CO² = CI² + IO²
10² = CI² + 5²
CI² = 75
⇒ CI = (cm)
⇒ CD = 2CI = 2 . = (cm)
Câu 125:
Có tất cả 18 táo, cam và xoài. Số quả cam bằng số quả táo. Số quả xoài gấp 3 lần số quả cam. Tính số quả mỗi loại?
 Xem đáp án
Xem đáp án
Gọi số quả cam là a
Thì số quả táo là 2a
Số quả xoài là 3a
Ta có: a + 2a + 3a = 18
6a = 18
a = 3
Vậy số quả cam là 3 quả.
Số quả táo là:
3 . 2 = 6 (quả).
Số quả xoài là:
3 . 3 = 9 (quả).
Câu 126:
Nêu cách tính góc tạo bởi kim giờ và kim phút.
 Xem đáp án
Xem đáp án
Đồng hồ hình tròn có 12 con số ứng với 360 độ.
60 phút thì kim phút sẽ quay được 360 độ nên 1 phút thì kim phút sẽ quay được:
360 : 60 = 6 (độ)
12 giờ, kim giờ sẽ quay được 360 được nên 1 giờ thì kim giờ sẽ quay được:
360 : 12 = 30 (độ)
1 phút kim giờ quay được:
30 : 60 = 0,5 (độ)
Gỉa sử góc khi chỉ a giờ b phút thì được tính như sau:
= .
Câu 127:
Một bếp ăn dự trữ đủ gạo cho 120 người ăn trong 12 ngày. Nếu chỉ có 80 người thực ăn và mức ăn của mỗi người như nhau thì chỗ gạo dự trữ đó đủ dùng trong bao nhiêu ngày?
 Xem đáp án
Xem đáp án
1 người ăn hết số gạo trong số ngày là:
120 . 12 = 1440 (ngày)
80 người ăn hết số gạo là:
1440 : 80 = 18 (ngày)
Đáp số: 18 ngày.
Câu 128:
Thu gọn S = x0 + x1 + … + xn.
 Xem đáp án
Xem đáp án
S = x0 + x1 + … + xn
S . x = x1 + x2 + … + xn+1
S.x – S = (x1 + x2 + … + xn+1) – (x0 + x1 + … + xn)
S (x–1) = xn+1 – x0
S =
S = .
Câu 129:
Một mảnh đất hình chữ nhật có chiều rộng bằng chiều dài. Nếu chiều rộng tăng thêm 9m, chiều dài bớt đi 9m thì mảnh đất trở thành hình vuông. Tính diện tích mảnh đất đó?
 Xem đáp án
Xem đáp án
Hiệu chiều dài và chiều rộng là:
9 + 9 = 18 (cm)
Chiều rộng mảnh đất là:
18 : (5 – 2) . 2 = 12 (cm)
Chiều dài mảnh đất là:
12 + 18 = 30 (cm)
Diện tích mảnh đất là:
30 . 12 = 360 (cm2).
Đáp số: 360 cm2.
Câu 130:
Có hai xe hàng, xe thứ nhất chở được 1 tấn 8 tạ hàng, xe thứ 2 hơn xe thứ nhất 4 tạ hàng. Hỏi cả hai xe chở được bao nhiêu tạ hàng ?
 Xem đáp án
Xem đáp án
Đổi: 1 tấn 8 tạ = 18 tạ
Xe thứ hai chở được:
18 + 4 = 22 (tạ)
Cả hai xe chở được số tạ hàng là:
18 + 22 = 40 (tạ)
Đáp số : 40 tạ hàng
Câu 131:
Một cửa hàng bán gạo ngày thứ nhất bán được 252kg. Ngày thứ hai bán được số gạo bán ngày đầu ngày thứ ba bán được gấp đôi ngày thứ nhất. Hỏi trung bình mỗi ngày cửa hàng bán được bao nhiêu kg gạo?
 Xem đáp án
Xem đáp án
Ngày 2 bán được số kg gạo là:
252 : 3 = 84 (kg)
Ngày 3 bán được số kg gạo là:
252 . 2 = 504 (kg)
Trung bình mỗi ngày cửa hàng bán được số kg gạo là:
(252 + 84 + 504) : 3 = 280 (kg)
Đáp số: 280 kg.
Câu 132:
Tính chu vi của hình tam giác ABC biết cạnh ngắn nhất là AB = 3,25cm, ngắn hơn cạnh AC là 1,5cm và ngắn hơn cạnh BC là 1,75cm.
 Xem đáp án
Xem đáp án
Độ dài cạnh AC là:
3,25 + 1,5 = 4,75 (cm).
Độ dài cạnh BC là:
3,25 + 1,75 = 5 (cm).
Chu vi hình tam giác ABC là:
3,25 + 4,75 + 5 = 13 (cm).
Câu 133:
 Xem đáp án
Xem đáp án
Đổi: 9m = 90dm, 6m = 60dm
Diện tích căn phòng là:
90 . 60 = 5400 (dm2)
Diện tích viên gạch là:
3 . 3 = 9 (dm2)
Cần số viên gạch là:
5400 : 9 = 600 (viên)
Đáp số: 600 viên gạch.
Câu 134:
Phân tích đa thức thành nhân tử: ab(a + b) – bc(b + c) – ac(c – a).
 Xem đáp án
Xem đáp án
ab(a + b) – bc(b + c) – ac(c – a)
= a2b + ab2 – bc(b + c) – ac2 + a2c
= (a2b + a2c) + (ab2 – ac2) – bc(b + c)
= a2(b + c) + a(b + c)(b – c) – bc(b + c)
= (b + c)(a2 + ab – ac – bc)
= (b + c)(a + b)(a – c).
Câu 135:
Cho a3 + b3 + c3 = 3abc và a, b, c > 0. Chứng minh rằng: a = b = c.
 Xem đáp án
Xem đáp án
a3 + b3 + c3 = 3abc
(a + b + c)(a2 + b2 + c2 – ab – ac – bc) = 0
Vì a + b + c > 0 nên a2 + b2 + c2 – ab – ac – bc = 0
⇔ 2a2 + 2b2 + 2c2 – 2ab – 2ac – 2bc = 0
⇔ (a–b)2 + (b–c)2 + (c–a)2 = 0
Vì (a–b)2 + (b–c)2 + (c–a)2 ≥ 0 với mọi a, b, c nên để đẳng thức xảy ra thì:
hay
Vậy a = b = c.
Câu 136:
Một mặt hàng tăng giá 25%. Sau một thời gian, muốn trở lại giá cũ thì số phần trăm phải giảm đi là bao nhiêu?
 Xem đáp án
Xem đáp án
Tổng số giá cũ và giá tăng là:
25 % + 100% = 125 %
Cần giảm giá để giá như ban đầu là:
25% : 125% = hay 20%
Vậy cần giảm 20%.
Câu 137:
Một số sau khi giảm đi 20% thì phải tăng thêm bao nhiêu phần trăm số mới để lại được số cũ?
 Xem đáp án
Xem đáp án
Một số giảm đi 20% tức là giảm đi của nó.
Số mới còn lại:
100% − 20% = 80% (số cũ)
Để số mới trở lại số cũ thì cần tăng thêm:
(100% : 80%) − 100% = 25%
Vậy phải giảm đi 25% để lại được số ban đầu.
Câu 138:
Hà làm được 16 bông hoa, Hằng làm được 19 bông hoa. Lan làm được số bông hoa nhiều hơn mức trung bình của cả 3 bạn là 5 bông. Hỏi cả 3 bạn làm được bao nhiêu bông hoa?
 Xem đáp án
Xem đáp án
Trung bình 3 bạn làm được số bông hoa là:
(16 + 19 + 5) : 2 = 20 (bông hoa)
Cả ba bạn làm được số bông hoa là:
20 × 3 = 60 (bông hoa)
Đáp số: 60 bông hoa.
Câu 139:
Một mảnh đất hình thang có tổng độ dài hai đáy là 49 m. Nếu kéo dài đáy bé thêm 4,5m và đáy lớn thêm 12,5m về cùng một phía thì diện tích mảnh đất sẽ tăng thêm 144,5 m2. Tính diện tích mảnh đất hình thang lúc đầu.
 Xem đáp án
Xem đáp án
Chiều cao của hình thang đó là :
2 × 144,5 : (12,5 + 4,5) = 17(m).
Diện tích mảnh đất hình thang lúc đầu là :
17 × (49 : 2) = 416,5 (m²).
Đáp số : 416,5 m² .
Câu 140:
Một phân xưởng được giao sản xuất một lô hàng. Ban quản lý phân xưởng tính rằng nếu 12 công nhân, mỗi người sản xuất 50 sản phẩm một ngày thì sẽ hoàn thành trong 20 ngày. Hỏi nếu 20 công nhân, mỗi người làm 60 sản phẩm một ngày thì sẽ hoàn thành trong bao nhiêu ngày?
 Xem đáp án
Xem đáp án
Phân xưởng phải sản xuất:
12 × 50 × 20 = 12000 (sản phẩm).
Nếu 20 công nhân, mỗi người làm 60 sản phẩm 1 ngày thì sẽ hoàn thành trong:
12000 : 20 : 60 = 10 (ngày).
Đáp số: 10 ngày.
Câu 141:
Một sân vận động hình chữ nhật được vẽ theo tỉ lệ 1 : 3000 và chiều dài 6cm chiều rộng 3cm. Hỏi diện tích sân vận động đó bằng bao nhiêu mét vuông?
 Xem đáp án
Xem đáp án
Chiều dài thật của sân vân động là :
6 . 3000 = 18000 (cm) = 180 m
Chiều rộng thật của sân vân động là :
3 . 3000 = 9000 (cm) = 90m
Diện tích sân vận động là :
180 . 90 = 16200 (m2)
Đáp số: 16200 m2.
Câu 142:
Có một số sách khi xếp thành từng bó 8 cuốn, 10 cuốn, 14 cuốn và 20 cuốn thì vừa đủ. Biết số sách trong khoảng từ 250 đến 400 cuốn. Hãy tính số sách đó.
 Xem đáp án
Xem đáp án
Số sách đã cho là bội chung của 8, 10, 14, 20 và thuộc khoảng từ 250 đến 400.
Ta có:
8 = 23
10 = 2.5
14 = 2.7
20 = 22.5
BCNN (8, 10, 14, 20) = 23 . 5 . 7 = 280
Mà số sách trong khoảng từ 250 đến 400 cuốn nên số sách đã cho là 280 cuốn.
Câu 143:
Dùng cả ba chữ số 3, 4, 5. Hãy ghép thành các số tự nhiên có ba chữ số:
a) Lớn nhất và chia hết cho 2.
 Xem đáp án
Xem đáp án
a) Vì số cần tìm chia hết cho 2 nên chữ số tận cùng phải là 4; số lớn nhất nên chữ số hàng trăm là 5. Vậy số cần tìm là 534.
Câu 144:
 Xem đáp án
Xem đáp án
b) Vì số cần tìm chia hết cho 5 nên chứ số tận cùng phải là 5; số nhỏ nhất nên chữ số hàng trăm là 3. Vậy số cần tìm là 345.
Câu 145:
Để lát 1 phòng có chiều dài 20m, chiều rộng 8m, bác Hà dùng loại gạch men hình vuông có cạnh dài 40cm. Hỏi cần bao nhiêu viên gạch men để vừa đủ lát hết nền căn phòng? (Biết mạch vữa có diện tích không đáng kể).
 Xem đáp án
Xem đáp án
Diện tích căn phòng là:
20 . 8 = 160 (m2) = 1600000 (cm2).
Diện tích mỗi viên gạch là :
40 . 40 = 1600 (cm2).
Số viên gạch lát được là :
1600000 : 1600 = 1000 (viên )
Đáp số: 1000 viên gạch.
Câu 146:
 Xem đáp án
Xem đáp án
1 hm2 = 10000 m2
hm2 = 10000 . = 6000 m2
Câu 147:
Cho x, y thuộc ℕ. Chứng minh rằng N = (x – y)(x – 2y)(x – 3y)(x – 4y) + y4 là số chính phương.
 Xem đáp án
Xem đáp án
N = (x – y)(x – 2y)(x – 3y)(x – 4y) + y4
N = [(x – y)(x – 4y)][(x – 2y)(x – 3y)] + y4
N = (x2 – 5xy + 4y2)(x2 – 5xy + 6y2) + y4
Đặt x2 – 5xy + 5y2 = a, ta được:
N = (a – y2)(a+y2) + y4
N = a2 – y4 + y4
N = a2.
Vậy N là số chính phương.
Câu 148:
Một phân xưởng được giao sản xuất một lô hàng. Ban quản lý phân xưởng tính rằng nếu 12 công nhân, mỗi người sản xuất 50 sản phẩm một ngày thì sẽ hoàn thành trong 20 ngày. Hỏi nếu 20 công nhân, mỗi người làm 60 sản phẩm một ngày thì sẽ hoàn thành trong bao nhiêu ngày?
 Xem đáp án
Xem đáp án
Phân xưởng phải sản xuất:
12 × 50 × 20 = 12000 (sản phẩm).
Nếu 20 công nhân, mỗi người làm 60 sản phẩm 1 ngày thì sẽ hoàn thành trong:
12000 : 20 : 60 = 10 (ngày).
Đáp số: 10 ngày.
Câu 149:
 Xem đáp án
Xem đáp án
(–6x3y7 . 5x2y2 – 15x4y5) (x2 + 1)
= (–30x5y9 – 15x4y5) (x2 + 1)
= –30x7y9 – 15x6y5 – 30x5y9 – 15x4y5
= 15x4y5 (–2x3y4 – x – 2xy4 – 1).
= 15x4y5 [–2xy4(x2 + 1) – (x + 1)]
Câu 150:
Kết quả của phép tính: 278145 chia 35 là bao nhiêu?
 Xem đáp án
Xem đáp án
278145 : 35 = 7947.
Vậy kết quả của phép tính là 7947.
Câu 151:
Điền vào chỗ trống: 3 tấn 218 kg = … tấn
 Xem đáp án
Xem đáp án
Vì 1 tấn = 1000 kg nên 1 kg = 0,0001 tấn
3 tấn 218 kg = 3,218 tấn.
Câu 152:
Tìm tập hợp các số tự nhiên n vừa chia hết cho 2, vừa chia hết cho 5 và 136 < n < 182.
 Xem đáp án
Xem đáp án
Vì 136 < n < 182 nên n là số có 3 chữ số.
Để n vừa chia hết cho 2 vừa chia hết cho 5 thì chữ số hàng đơn vị của n bằng 0.
Vậy tập hợp các số tự nhiên n thỏa mãn là: 140; 150; 160; 170; 180.
Câu 153:
Người ta lát sàn một căn phòng hình chữ nhật có chiều dài 6m, chiều rộng 4m bằng những mảnh gỗ hình chữ nhật có chiều dài 1m20cm, chiều rộng 20 cm. Hỏi cần bao nhiêu mảnh gỗ để lát kín sàn căn phòng đó?
 Xem đáp án
Xem đáp án
Đổi : 1m 20cm = 120 cm.
Diện tích căn phòng đó là :
6 . 4 = 24 (m2) = 240000 (cm2)
Diện tích một mảnh gỗ hình chữ nhật là :
120 . 20 = 2400 (cm2)
Cần số mảnh gỗ để lát kín sàn căn phòng đó là :
240000 : 2400 = 100 (mảnh gỗ)
Đáp số: 100 mảnh gỗ.
Câu 154:
Tìm x, y biết: 9x2 + 6x + 4y2 – 8y + 5 = 0
 Xem đáp án
Xem đáp án
9x2 + 6x + 4y2 – 8y + 5 = 0
⇔ (9x2 + 6x + 1) + (4y2 – 8y + 4) = 0
⇔ (3x + 1)2 + (2y – 2)2 = 0 (*)
Vì (3x + 1)2 + (2y – 2)2 ≥ 0 với mọi x,y nên để (*) xảy ra thì:
Hay
Vậy (x; y) = .
Câu 155:
Trong số 45 học sinh của lớp 10A có 15 bạn được xếp loại học lực giỏi, 20 bạn được xếp loại hạnh kiểm tốt, trong đó có 10 bạn vừa học lực giỏi, vừa có hạnh kiểm tốt. Hỏi
a) Lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải học lực giỏi hoặc có hạnh kiểm tốt?
 Xem đáp án
Xem đáp án
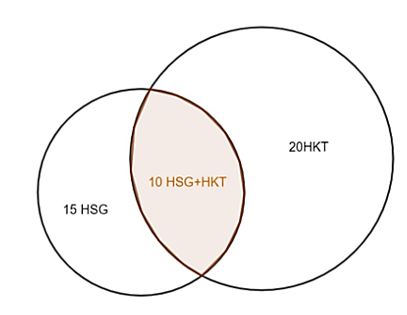
a) Các bạn được học lực giỏi = 15.
Các bạn được hạnh kiểm tốt = 20.
Số bạn học lực tốt và hạnh kiểm tốt = 10.
⇒ Số bạn được hạnh kiểm tốt mà không được học lực giỏi là:
15 – 10 = 5 (bạn).
Số bạn được học lực giỏi mà không được hạnh kiểm tốt là:
20 – 10 = 10 (bạn)
Vậy số bạn được khen thưởng = (số bạn được hạnh kiểm tốt mà không được học lực giỏi)
+ (số bạn được học lực giỏi mà không được hạnh kiểm tốt) + (số bạn vừa được học lực giỏi, vừa được hạnh kiểm tốt)
= 5 + 10 + 10 = 25 (bạn).
Câu 156:
b) Lớp 10A có bao nhiêu bạn chưa được xếp loại học lực giỏi và chưa có hạnh kiểm tốt?
 Xem đáp án
Xem đáp án
b) Số học sinh chưa được xếp loại học lực giỏi và chưa có hạnh kiểm tốt là:
45 – 25 = 15 (bạn).
Câu 157:
Cho tam giác vuông tại A, AB = 6cm, BC = 10cm. Tính AC.
 Xem đáp án
Xem đáp án
Áp dụng định lí Pitago vào tam giác ABC vuông tại A, có:
AB2 + AC2 = BC2
⇒ AC = (cm)
Vậy AC = 8 cm.
Câu 158:
 Xem đáp án
Xem đáp án
76 + 75 – 74
= 74 (72 + 7 – 1)
= 74 . 55
Vì 55 ⋮ 55 nên 74 . 55 ⋮ 55.
Vậy 76 + 75 – 74 chia hết cho 55.
Câu 159:
Cho bốn chữ số 0; 9; 3; 6. Hãy viết tất cả các số thập phân nhỏ nhất với bốn chữ số đã cho, biết phần thập phân có ba chữ số.
 Xem đáp án
Xem đáp án
Số thập phân cần tìm là: 0,369.
Câu 160:
Từ 5 chữ số 0,1,2,3,4 có thể viết được bao nhiêu số có 4 chữ số khác nhau là số chẵn.
 Xem đáp án
Xem đáp án
Gọi số có 4 chữ số khác nhau thỏa mãn yêu cầu là (a khác 0; a, b, c, d < 10)
Để là số chẵn thì d = 0, 2, 4
+ Với d = 0, thì a có 4 cách chọn, b có 3 cách chọn, c có 2 cách chọn
⇒ Số các số lập được = 4.3.2 = 24 (số)
+ Với d = 2, thì a có 3 cách chọn, b có 3 cách chọn, c có 2 cách chọn
⇒ Số các số lập được = 3.3.2 = 18 (số)
+ Với d = 4, thì a có 3 cách chọn, b có 3 cách chọn, c có 2 cách chọn
⇒ Số các số lập được = 3.3.2 = 18 (số)
Vậy lập được:
24 + 18 + 18 = 60 (số).
Câu 161:
Cho tam giác ABC nhọn (AB < AC).Các đường cao AD, BE, CF cắt nhau tại H. Gọi M là trung điểm của BC, K đối xứng với H qua M.
a) Chứng minh BHCK là hình bình hành.
 Xem đáp án
Xem đáp án

a) K đối xứng với H qua M nên M là trung điểm KH
Tứ giác BHCK có hai đường chéo BC và HK cắt nhau tại trung điểm M của mỗi đường nên BHCK là hình bình hành
Câu 162:
 Xem đáp án
Xem đáp án
b) BHCK là hình bình hành nên BK // HC
Mà HC vuông góc với AB nên BK vuông góc với AB
Câu 163:
c) Gọi I là điểm đối xứng với H qua BC. Chứng minh tứ giác BIKC là hình thang cân.
 Xem đáp án
Xem đáp án
c) Gọi N là giao điểm của HI và BC thì N là trung điểm của HI
MN là đường trung bình trong tam giác HIK nên MN // IK
Hay IK // BC nên BIKC là hình thang
I đối xứng với H qua BC nên BN là đường trung trực của HI nên BH = BI
Vì BHCK là hình bình hành nên BH = CK
Suy ra BI = CK nên BIKC là hình thang cân.
Câu 164:
 Xem đáp án
Xem đáp án
d) Vì BK // HC hay GK // HC nên GKHC là hình thang
Để HGKC là hình thang cân thì HG = CK hay
Mà CK = BI = BH nên HG = CK = BH.
Ta có: BK // HC suy ra: CK ⊥ AC.
Để
⇒ 90° – = 90° –
⇒ =
Vậy để GKCH là hình thang cân thì CH phải là phân giác trong của mà CH ⊥ AB nên tam giác ABC phải là tam giác cân.
Câu 165:
Cho tập hợp A = {1; 2; 3; 4; 5; 6; 7; 8; 9}. Hỏi có bao nhiêu số có 4 chữ số khác nhau sao cho tổng chữ số thứ 1, thứ 3 bằng tổng chữ số thứ 2, thứ 4?
 Xem đáp án
Xem đáp án
Gọi những số cần tìm có dạng
Theo giả thiết ta có: a + c = b + d.
Từ tập A ta có các bộ số có tổng bằng nhau là: {1; 8}, {2; 7}, {3; 6},{4; 5}
Ta chọn 2 trong 4 bộ trên, thì có: cách chọn
Đảo chữ số a và c, số cách chọn là: 2!
Đảo chữ số b và d, số cách chọn là: 2!
Vậy số các số có 4 chữ số khác nhau lập được: .2!. 2! = 48 (số).
Câu 166:
Chứng minh rằng giá trị của biểu thức không phụ thuộc vào biến
a) (x + 2)2 – 2(x + 2)(x + 8) + (x – 8)2.
 Xem đáp án
Xem đáp án
a) (x + 2)2 – 2(x + 2)(x + 8) + (x – 8)2
= [(x + 2) – (x – 8)]2
= 102
= 100.
Câu 167:
Chứng minh rằng giá trị của biểu thức không phụ thuộc vào biến
b) (x + y – z – t)2 – (z + t – x – y)2.
 Xem đáp án
Xem đáp án
b) (x + y – z – t)2 – (z + t – x – y)2
= (x + y – z – t + z + t – x – y)( x + y – z – t – z – t + x + y)
= 0 . (2x + 2y – 2z – 2t)
= 0.
Câu 168:
 Xem đáp án
Xem đáp án
E = 7 + 72 + … + 74n–1 + 74n
E = (7 + 72 + 73 + 74) + (75 + 76 + 77 + 78) + … + (74n–3 + 74n–2 + 74n–1 + 74n)
E = 7 (1 + 7 + 72 + 73) + 75(1 + 7 + 72 + 73) + … + 74n–3 (1 + 7 + 72 + 73)
E = 400 (7 + 75 + … + 74n–3)
Vì 400 ⋮ 400 nên 400 (7 + 75 + … + 74n–3) ⋮ 400
Vậy E ⋮ 400.
Câu 169:
Chứng minh rằng 100 không phải là số lập phương.
 Xem đáp án
Xem đáp án
Ta thấy: 100 = 102
Nên 100 là số chính phương, không phải là số lập phương.
Câu 170:
 Xem đáp án
Xem đáp án
Hiệu ban đầu của hai số là:
537 – 357 + 173 = 351.
Số lớn là:
(4735 + 351) : 2 = 2543.
Số bé là:
4735 – 2543 = 2192.
Vậy số lớn là 2543, số bé là 2192.
Câu 171:
Một hình thang có diện tích là 6,3 m2 và trung bình cộng của 2 đáy là m. Tính chiều cao của hình thang.
 Xem đáp án
Xem đáp án
Tổng 2 đáy là:
2 . = 2,25 (m).
Chiều cao của hình thang là:
(6,3 . 2) : 2,25 = 5,6 (m).
Đáp số: 5,6 m.
Câu 172:
Một hình thang có đáy lớn là 35,6m; đáy lớn hơn đáy bé 9,7 m và chiều cao bằng tổng hai đáy. Tính diện tích mảnh đất đó.
 Xem đáp án
Xem đáp án
Đáy bé của mảnh đất hình thang đó là:
35,6 − 9,7 = 25,9 (m)
Chiều cao của mảnh đất hình thang đó là:
. (35,6 + 25,9) = 41(m)
Diện tích mảnh đất hình thang đó là:
(35,6 + 25,9) . 41 : 2 = 1260,75 (m²).
Đáp số: 1260,75 m2.
Câu 173:
Một thửa ruộng hình thang có trung bình của hai đấy là 60m, đường cao bằng cạnh của hình vuông của một hình vuông có chu vi 160m. Người ta cấy lúa trên thửa ruộng này cứ 3 ha thu được 13,5 tấn thóc thì thửa ruộng thu được bao nhiêu tấn thóc?
 Xem đáp án
Xem đáp án
Chiều cao của thửa ruộng hình thang là:
160 : 4 = 40 (m).
Tổng 2 đáy của thửa ruộng là:
60 . 2 = 120 (m).
Diện tích thửa ruộng hình thang là:
(120 . 40) : 2 = 2400 (m2).
Đổi: 2400 m2 = 0,24 ha.
Số tấn thóc thửa ruộng thu được là:
(0,14 : 3) . 13,5 = 1,08 (tấn).
Đáp số: 1,08 tấn.
Câu 174:
1 hình thang có trung bình cộng 2 đáy là 9,7 m và chiều cao là 6,8 m thì diện tích hình thang là?
 Xem đáp án
Xem đáp án
Tổng độ dài 2 đáy là:
9,7 × 2 = 19,4 (m)
Diện tích hình thang là:
19,4 × 6,8 : 2 = 65,96 (m2).
Đáp số: 65,96 m2.
Câu 175:
Người ta thả cá ở một hồ hình chữ nhật, chiều rộng là 400m và bằng chiều dài, cứ mỗi ha thu được 10 tấn cá một năm. Tính:
a) Diện tích hồ ra mét vuông, ra ha.
 Xem đáp án
Xem đáp án
a) Chiều dài hồ hình chữ nhật là:
400 : = 450 (m).
Diện tích hồ hình chữ nhật là:
450 . 400 = 180000 (m2) = 18 ha.
b) Sản lượng hồ đó mỗi năm là:
18 . 10 = 180 (tấn).
Đáp số: a) 180000 m2 = 18 ha.
b) 180 tấn.
Câu 176:
Người ta trồng ngô trên một thửa ruộng hình chữ nhật có chiều rộng 60 m. Chiều dài bằng chiều rộng. Biết rằng trung bình cứ 100 m2 thu hoạch được 70 kg ngô. Hỏi trên cả thửa ruộng đó người ta thu hoạch được bao nhiêu tạ ngô?
 Xem đáp án
Xem đáp án
Chiều dài thửa ruộng là:
60 . 5 : 3 = 100 (m)
Diện tích thửa ruộng là:
100 . 60 = 6000 (m2)
Người ta thu hoạch được là:
6000 : 100 . 70 = 4200 (kg)
Đổi 4200 kg = 4,2 tạ.
Vậy trên cả thửa ruộng đó người ta thu hoạch được 4,2 tạ ngô.
Câu 177:
Ông Hùng mua 300 viên gạch hoa hình vuông cạnh 30cm để lát nền một phòng khách và một phòng ngủ thì vừa hết. Hỏi phòng khách nhà ông Hùng có diện tích bao nhiêu mét vuông? Biết phòng ngủ có diện tích 9 m2 và diện tích phần mạch vữa không đáng kể.
 Xem đáp án
Xem đáp án
Đổi: 9 m2 = 90000 cm2
Diện tích của một viên gạch là:
30 . 30 = 900 (viên)
Vậy để lát hết phòng ngủ cần số viên gạch là:
90000 : 90 = 100 (viên)
Số viên gạch dùng để lát phòng khách là:
300 – 100 = 200 (viên)
Diện tích của phòng khách là:
200 . 900 = 180000 (cm2) = 18 m2.
Đáp số: 18 m2.
Câu 178:
Cho 3 chữ số 4, 2, 6.
a) Hãy viết tất cả các số thập phân có 3 chữ số khác nhau và nhỏ hơn 100.
 Xem đáp án
Xem đáp án
a) Các số thập phân có ba chữ số khác nhau và nhỏ hơn 100 là:
4,26; 4,62; 6,24 ; 6,42; 2,46; 2,64; 42,6; 46,2; 24,6; 26,4; 62,4; 64,2
Câu 179:
Cho 3 chữ số 4, 2, 6.
b) Tính tổng các số mà viết được bằng cách thuận tiện nhất.
 Xem đáp án
Xem đáp án
b) Tính tổng các số thập phân:
4,26 + 4,62 + 6,24 + 6,42 + 2,46 + 2,64 + 42,6 + 46,2 + 24,6 + 26,4 + 62,4 + 64,2
= (4,26 + 6,24) + (2,46 + 2,64) + (4,62 + 6,42) + (42,6 + 62,4) + (46,2 + 64,2) + (24,6 + 26,4)
= 10,5 + 5,1 + 11,04 + 105 + 110,4 + 51
= 10,5 + 105 + 110,4 + 11,04 + 5,1 + 51
= 115,5 + 56,1 + 121,44
= 293,04.
Câu 180:
So sánh: 2 hm2 46 m2 và 246 dam2.
 Xem đáp án
Xem đáp án
2 hm2 46 m2 = 200,46 dam2
Vậy 2 hm2 46 m2 < 246 dam2.
Câu 181:
So sánh 334 và 520.
 Xem đáp án
Xem đáp án
334 > 330 = 33.10 = (33)10 = 2710 > 2510
Mà 2510 = 520
Vậy 334 > 520.
Câu 182:
 Xem đáp án
Xem đáp án
3x + 3x+2 = 270
3x (1 + 32) = 270
3x = 270 : 10
3x = 27
3x = 33
Vậy x = 3.
Câu 184:
Chứng tỏ rằng D chia hết cho 13 biết D = 1 + 3 + 32 + … + 398.
 Xem đáp án
Xem đáp án
D = 1 + 3 +32 + … + 398
D = (1 + 3 + 32) + (33 + 34 + 35) + … + (396 + 397 + 398)
D = 13 + 33 (1 + 3 + 32) + … + 396(1 + 3 + 32)
D = 13 (1 + 33 + … + 396)
Vì 13 ⋮ 13 nên 13 (1 + 33 + … + 396) ⋮ 13
Vậy D ⋮ 13.
Câu 186:
Một mảnh vườn hình chữ nhật có chu vi là 252 m và chiều rộng bằng chiều dài. Tính diện tích của mảnh vườn đó
 Xem đáp án
Xem đáp án
Nửa chu vi mảnh vườn là:
252 : 2 = 126 (m)
Chiều rộng mảnh vườn là:
126 : (4 + 5) . 4 = 56(m)
Chiều dài mảnh vườn là:
126 – 56 = 70 (m)
Diện tích mảnh vườn là:
56 . 70 = 3920 (m²).
Đáp số: 3920 m2.
