Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 20)
-
1924 lượt thi
-
82 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Tìm số tự nhiên a nhỏ nhất sao cho chia a cho 3; 5; 7 được số dư theo thứ tự là 2; 3; 4.
 Xem đáp án
Xem đáp án
Do a chia cho 3 dư 2, chia cho 5 dư 3, chia cho 7 dư 4 nên 2a chia cho 3, 5, 7 dư 1.
Suy ra 2a – 1 chia hết cho 3, 5, 7 hay 2a – 1 là bội chung của 3, 5, 7.
Như vậy để a là số tự nhiên nhỏ nhất thỏa mãn yêu cầu đề bài thì 2a – 1 phải là BCNN(3, 5, 7).
Ta có: BCNN(3, 5, 7) = 3.5.7 = 105 nên 2a – 1 = 105 suy ra a = 53.
Vậy số cần tìm là 53.
Câu 2:
Tìm số tự nhiên có hai chữ số biết rằng khi chia số đó cho hiệu các chữ số của nó ra được thương là 28 và dư 1.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là và hiệu các chữ số của nó là c.
Theo để bài ta có:
= 28 × c + 1
Vì < 100 nên 28c + 1 < 100, do đó c < 4 (vì 28 × 4 + 1 = 113).
Mà c > 0 để > 10.
Suy ra c = 1; 2 hoặc 3.
– Nếu c = 1 thì = 29 (loại vì 9 – 2 = 7 ≠ 1)
– Nếu c = 2 thì = 57 (thỏa mãn)
– Nếu c = 3 thì = 85 (thỏa mãn).
Vậy số cần tìm là 57 và 85.
Câu 3:
Giải phương trình: x4 = 2x2 + 8x + 3.
 Xem đáp án
Xem đáp án
x4 = 2x2 + 8x + 3
⇔ x4 + 2x2 + 1 – 4x2 – 8x – 4 = 0
⇔ (x2 + 1)2 – 4(x + 1)2 = 0
⇔ (x2 + 2x + 3)(x2 – 2x – 1) = 0
Vì x2 + 2x + 3 = (x + 1)2 + 2 > 0 với mọi x nên ta có:
x2 – 2x – 1 = 0
⇔ (x – 1)2 = 2
⇔
Vậy x = hoặc x = .
Câu 7:
Ba bạn Sơn, Minh, Hùng có tất cả 84 viên bi. Biết số viên bi trung bình của Sơn và Minh nhiều hơn số viên bi trung bình của Minh và Hùng là 4 viên bi và ít hơn số viên bi trung bình của Hùng và Sơn là 4 viên bi. Khi đó số viên bi của Hùng là bao nhiêu viên bi?
 Xem đáp án
Xem đáp án
Gọi số bi của Sơn, Minh, Hùng lần lượt là a, b, c.
Ta có:
a + b + c = 84 (1)
⇔ a = c + 8 (2)
⇔ b + 8 = c ⇔ b = c – 8 (3)
Thế (2), (3) vào (1) ta có:
c + 8 + c – 8 + c = 84
3c = 84
c = 84 : 3
c = 28.
Vậy Hùng có 28 viên bi.
Câu 8:
Chứng minh rằng A chia hết cho 6 biết A = 2 + 22 + 23 + … + 2100.
 Xem đáp án
Xem đáp án
A = 2 + 22 + 23 + … + 2100
A = (2 + 22) + (23 + 24) + … + (299 + 2100)
A = 6 + 22 (2 + 22) + … + 298 (2 + 22)
A = 6 (1 + 22 + … + 298)
Vì 6 chia hết cho 6 nên 6 (1 + 22 + … + 298) chia hết cho 6.
Vậy A chia hết cho 6.
Câu 9:
Hai phân xưởng làm được 299 sản phẩm. Phân xưởng A làm được ít hơn phân xưởng B 83 sản phẩm. Hỏi mỗi phân xưởng làm được bao nhiêu sản phẩm?
 Xem đáp án
Xem đáp án
Phân xưởng A làm được số sản phẩm là:
(299 – 83) : 2 = 108 (sản phẩm)
Phân xưởng B làm được số sản phẩm là:
108 + 83 = 191 (sản phẩm).
Đáp số: phân xưởng A: 108 sản phẩm; phân xưởng B: 191 sản phẩm.
Câu 10:
Hiện nay Hùng nhiều hơn Minh 12 tuổi. Tính tuổi của Hùng hiện nay, biết rằng khi tuổi của Minh bằng tuổi của Hùng hiện nay thì tuổi của Minh bằng lần tuổi của Hùng khi đó?
 Xem đáp án
Xem đáp án
Gọi số tuổi của Hùng hiện nay là a (a > 12)
Thì số tuổi của Minh hiện nay là a – 12
Nếu tuổi Minh bằng tuổi Hùng hiện nay tức là tuổi Minh bằng a
Khi đó tuổi Hùng là a + 12
Ta có:
a = (a + 12)
a =
a = :
a = 18.
Vậy hiện nay Hùng 18 tuổi, Minh 6 tuổi.
Câu 11:
Lớp 4A quyên góp được 33 quyển vở, lớp 4B quyên góp được 28 quyển vở. Lớp 4C quyên góp được nhiều hơn lớp 4B 7 quyển vở. Hỏi trung bình mỗi lớp quyên góp được bao nhiêu quyển vở ?
 Xem đáp án
Xem đáp án
Số vở lớp 4C quyên góp được là:
28 + 7 = 35 (quyển)
Tổng số vở 3 lớp quyên góp được là:
33 + 28 + 35 = 96 (quyển)
Trung bình mỗi lớp quyên góp được số vở là:
96 : 3 = 32 (quyển)
Đáp số: 32 quyển.
Câu 12:
Một thửa ruộng hình chữ nhật có chiều dài là 360 m, chiều rộng bằng chiều dài. Hỏi thửa ruộng có diện tích bằng bao nhiêu mét vuông ?
 Xem đáp án
Xem đáp án
Chiều rộng thửa ruộng là:
360 × = 240 (m).
Diện tích thửa ruộng là:
360 × 240 = 86400 (m2).
Đáp số: 86 400 m2.
Câu 13:
Một thửa ruộng hình chữ nhật có nửa chu vi là 0,16 hm, chiều rộng bằng chiều dài. Trung bình cứ 500 m2 thì thu được 250 kg lúa. Hỏi người ta thu được bao nhiêu tấn lúa trên thửa ruộng ?
 Xem đáp án
Xem đáp án
Đổi 0,16 hm = 160 m.
Chiều rộng thửa ruộng là:
160 : (3 + 5) × 3 = 60 (m).
Chiều dài thửa ruộng là:
160 – 60 = 100 (m).
Diện tích thửa ruộng là:
60 × 100 = 6000 (m2).
Người ta thu được số kg lúa là:
6000 : 500 × 250 = 3000 (kg)
Đổi 3000 kg = 3 tấn.
Đáp số: 3 tấn lúa.
Câu 14:
Một mảnh đất hình chữ nhật có chiều dài 18m, chiều rộng bằng 12m. Người ta dành 20% diện tích mảnh đất để trồng hoa, còn lại là đất trồng rau. Tính diện tích trồng rau?
 Xem đáp án
Xem đáp án
Diện tích mảnh đất là:
18 × 12 = 216 (m²)
Diện tích đất trồng hoa là:
216 × 20 : 100 = 43,2 (m²)
Diện tích đất trồng rau là:
216 – 43,2 = 172,8 (m²)
Đáp số: 172,8 m².
Câu 15:
Một tấm biển quảng cáo hình chữ nhật có chiều dài 24 cm và gấp 4 lần chiều rộng. Diện tích tấm biển là?
 Xem đáp án
Xem đáp án
Chiều rộng tấm biển là:
24 : 4 = 6 (cm).
Diện tích tấm biển là:
24 × 6 = 144 (cm2).
Đáp số: 144 cm2.
Câu 16:
Một khu vườn trồng cây có tổng cộng 2280 cây ăn quả. Trong đó số cây cam chiếm 37,5 % tổng số cây. Số cây nhãn chiếm 25 % tổng số cây; còn lại là cây xoài. Tính số cây mỗi loại?
 Xem đáp án
Xem đáp án
Số cây cam là:
2280 × 37,5% = 855 (cây).
Số cây nhãn là:
2280 × 25% = 570 (cây).
Số cây xoài là:
2280 – 855 – 570 = 855 (cây).
Đáp số: Cam: 855 cây
Nhãn: 570 cây
Xoài 855 cây.
Câu 17:
Một xưởng may đã dùng đến 545 m vải để may quần áo. Trong đó số vải may quần chiếm 40% số vải đó. Hỏi số vải may áo là bao nhiêu mét?
 Xem đáp án
Xem đáp án
Số phần trăm vải chỉ may áo là:
100 – 40 = 60 (%)
Số vải may áo là:
545 × 60 : 100 = 327(m)
Đáp số: 327 m.
Câu 18:
Tìm phân số tối giản biết rằng phân số gấp 7 lần phân số .
 Xem đáp án
Xem đáp án
Ta có: = 7 .
+ 1 = 7 .
6 . = 1
= .
Vậy phân số cần tìm là .
Câu 19:
Một hình thoi có tổng độ dài hai đường chéo là 100 cm. Đường chéo AC bằng đường chéo BD. Tính diện tích hình thoi đó?
 Xem đáp án
Xem đáp án
Đường chéo AC có độ dài là:
100 : (2 + 3) × 2 = 40 (cm)
Đường chéo BD có độ dài là:
100 – 40 = 60 (cm)
Diện tích hình thoi đó là:
(40 × 60) : 2 = 1200 (cm2)
Đáp số: 1200 cm2.
Câu 20:
Độ dài hai đường chéo của một hình thoi là 100 cm, hiệu độ dài của chúng là 16 cm. Khi đó diện tích hình thoi bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Độ dài đường chéo thứ nhất là:
(100 – 16) : 2 = 42
Độ dài đường chéo thứ hai là:
42 + 16 = 58 (cm).
Diện tích hình thoi là:
(42 × 58) : 2 = 1218 (cm2).
Đáp số: 1218 cm2.
Câu 21:
Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài tại A. Vẽ dây AM của đường tròn (O) và dây AN của đường tròn (O') sao cho AM vuông góc AN.
Chứng minh OM // O'N.
 Xem đáp án
Xem đáp án
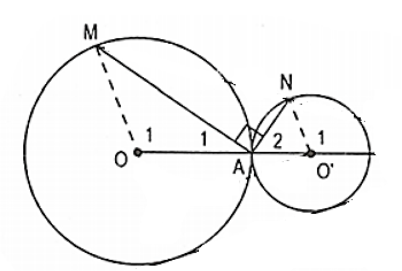
Ta có tam giác OAM cân tại O (do OM = OA = R) nên
Tam giác O'AN cân tại O' (do O'A = O'N = R') nên
Suy ra:
Mà 2 góc này ở vị trí đồng vị nên OM // O'N.
Câu 22:
Một cái xe đạp có giá 400 000 đồng nay hạ giá 15%. Hỏi cái xe đạp bây giờ là bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Số tiền mà xe đạp đã bị hạ xuống là:
400 000 : 100 × 15 = 60000 (đồng)
Xe đạp bây giờ có số tiền là:
400 000 – 60 000 = 340 000 (đồng)
Đáp số: 340 000 đồng.
Câu 23:
Tìm số nguyên tố p biết rằng p + 4; p + 6; p + 8; p + 10 đều là số nguyên tố.
 Xem đáp án
Xem đáp án
Với p = 2 ⇒ p + 4 = 6 (loại vì không là số nguyên tố)
Với p = 3 ⇒ p + 6 = 9 (loại vì không là số nguyên tố)
Với p > 3, vì p là số nguyên tố nên p không chia hết cho 3.
Do đó, p có dạng p = 3k + 1 hoặc p = 3k + 2
Với p = 3k + 1 ⇒ p + 8 = 3k + 1 + 8 = 3k + 9 ⋮ 3 (loại)
Với p = 3k + 2 ⇒ p + 10 = 3k + 2 + 10 = 3k + 12 ⋮ 3 (loại)
Vậy không có số nguyên tố nào thỏa mãn yêu cầu bài toán.
Câu 24:
Tìm một số thập phân có chữ số ở phần thập phân là 3 biết rằng nếu viết thêm chữ số 2 vào trước dấu phẩy thì tổng số mới và số cũ là 13,6.
 Xem đáp án
Xem đáp án
Gọi số thập phân ban đầu có dạng
Ta có:
+ = 13,6
A + 0,3 + (10A + 2) + 0,3 = 13,6
11A = 11
A = 1.
Vậy số thập phân cần tìm là 1,3.
Câu 25:
Muốn so sánh độ dài hai đoạn thẳng bằng compa ta làm thế nào?
 Xem đáp án
Xem đáp án
Dùng compa với độ mở sao cho 2 mũi nhọn compa trùng với 2 đầu của 1 đoạn thẳng.
Với cùng độ mở đó ta có thể so sánh với độ dài đoạn thẳng thứ 2.
Câu 26:
Một đội thợ muốn làm xong công việc cần 7 người làm trong 21 ngày. Nếu muốn làm xong công việc trong 5 ngày thì cần bao nhiêu người? (năng suất làm việc mỗi người như nhau)
 Xem đáp án
Xem đáp án
Muốn làm xong công việc trong 1 ngày thì cần:
21 .7 = 147 (người)
Ta có: 147 : 5 = 29,4
Vậy nếu muốn làm xong công việc trong 5 ngày thì cần 30 người.
Câu 27:
So sánh 637 và 1612.
 Xem đáp án
Xem đáp án
637 < 647 = (26)7 = 242
1612 = (24)12 = 248
Vì 248 > 242 nên 1612 > 637.
Câu 28:
Đội văn nghệ của một trường có 48 nam và 72 nữ về một huyện để biểu diễn. Muốn phục vụ đồng thời tại nhiều địa điểm, đội dự định chia thành các tổ gồm cả nam và nữ, số nam được chia đều vào các tổ, số nữ cũng vậy. Có thể chia được nhiều nhất thành bao nhiêu tổ ? Khi đó mỗi tổ có bao nhiêu nam, bao nhiêu nữ ?
 Xem đáp án
Xem đáp án
Gọi x là số tổ. Vì số nam được chia đều, số nữ cũng vậy nên mỗi tổ có cả nam và nữ đều bằng nhau. Do đó x là ƯC(48, 72).
Ta có:
48 = 24.3;
72 = 23.32
ƯCLN(48, 72) = 23.3 = 24.
⇒ x = ƯC(48, 72) = Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Số tổ có thể chia được nhiều nhất chính là ƯCLN (48, 72) = 24
Vậy x = 24 tổ.
Khi đó, mỗi tổ có 48 : 24 = 2 (nam) và 72 : 24 = 3 (nữ).
Câu 29:
Cho 8 số tự nhiên bất kì có 3 chữ số. Chứng minh rằng luôn tại 2 trong 8 số đó viết liền nhau tạo thành 1 số chia hết cho 7.
 Xem đáp án
Xem đáp án
Chia 1 số tự nhiên (trong 8 số đó) cho 7 ta thu được 1 số dư
⇒ Khi chia cả 8 số đó cho 7 ta sẽ thu được 8 số dư
Mà một phép chia cho 7 có thể dư 0; 1; 2; 3; 4; 5; 6
⇒ Có ít nhất 2 trong 8 số chia cho 7 thì cùng số dư
⇒ Hiệu 2 số đó chia hết cho 7
Gọi 2 số đó là và (0 ≤ a, b , c, d, e, f ≤ 9; a, d khác 0)
Không mất tính tổng quát, giả sử >
Ta có:
= 1000 +
⇔ = 1001 – +
⇔ = 7 . 143 . –
Vì 7 . 143 . chia hết cho 7 và chia hết cho 7 nên chia hết cho 7.
Vậy luôn tại 2 trong 8 số đó viết liền nhau tạo thành 1 số chia hết cho 7.
Câu 30:
Hùng muốn cắt một tấm bìa hình chữ nhật có kích thước 60 cm và 96 cm thành các mảnh nhỏ hình vuông bằng nhau. Tính độ dài lớn nhất của các hình vuông?
 Xem đáp án
Xem đáp án
60 = 22 . 3 . 5
96 = 25 . 3
Độ dài cạnh các hình vuông là ước của chiều dài và chiều rộng hình chữ nhật
Suy ra độ dài lớn nhất của các hình vuông là ƯCLN (chiều dài, chiều rộng)
Suy ra: cạnh = ƯCLN (60, 96) = 22 . 3 = 12
Vậy độ dài lớn nhất là 12 cm.
Câu 31:
Tìm số tự nhiên x biết 120 chia hết cho x; 300 chia hết cho x và 0 < x < 1200.
 Xem đáp án
Xem đáp án
Ta có: x ∈ BC (120, 300)
120 = 23 . 3 . 5
300 = 22 . 3 . 52
BCNN (120, 300) = 23 . 3 . 52 = 600
BC (120, 300) = B(60) = {0; 600; 1200; …}
Vì 0 < x < 1200 nên x = 600.
Vậy x = 600.
Câu 32:
Tìm bội chung nhỏ nhất của 125 và 100.
 Xem đáp án
Xem đáp án
125 = 53
100 = 22 . 52
BCNN (125; 100) = 22 . 53 = 500.
Câu 33:
Cho 2 số biết số lớn là 1516 và số này lớn hơn trung bình cộng của 2 số là 173. Tìm số bé.
 Xem đáp án
Xem đáp án
Trung bình cộng của 2 số là:
1516 – 173 = 1343
Tổng của 2 số là:
1343 × 2 = 2686
Số bé là:
2686 – 1516 = 1170
Đáp số: 1170.
Câu 34:
Tìm ƯCLN của 5661; 5291 và 4292.
 Xem đáp án
Xem đáp án
5661 = 32 . 17 . 37
5291 = 11 .13 . 37
4292 = 22 . 29 . 37
ƯCLN (5661; 5291; 4292) = 37.
Câu 35:
 Xem đáp án
Xem đáp án
Vì A là số nguyên nên 21 ⋮ (n – 4)
Suy ra: n – 4 ∈ Ư(21)
⇒ n – 4 ∈ {–1; 1; –3; 3; –7; 7; –21; 21}
⇒ n ∈ {3; 5; 1; 7; –3; 11; –17; 25}.
Câu 36:
 Xem đáp án
Xem đáp án
n3 (n2 – 7)2 – 36n
= n [n2 (n2 – 7)2 – 62]
= n [n (n2 – 7) – 6][ n (n2 – 7) + 6]
= n (n3 – 7n – 6)(n3 – 7n + 6)
= n (n3 – 3n2 + 3n2 – 9n + 2n – 6)( n3 + 3n2 – 3n2 – 9n + 2n + 6)
= n [(n2 (n – 3) + 3n (n – 3) + 2(n – 3)][(n2 (n + 3) – 3n (n – 3) + 2(n + 3)]
= n(n – 3)(n + 3)(n2 + 3n + 2)(n2 – 3n + 2)
= n(n – 3)(n + 3)(n + 1)(n + 2)(n – 1)(n – 2).
Ta thấy đây là 7 số tự nhiên liên tiếp nên sẽ tồn tại ít nhất 1 số chia hết cho 7.
Suy ra: tích của 7 số tự nhiên liên tiếp chia hết cho 7 hay n3 (n2 – 7)2 – 36n chia hết cho 7.
Vậy n3 (n2 – 7)2 – 36n chia hết cho 7.
Câu 37:
Khi lấy tổng của các số tự nhiên từ 1 đến 49 trừ đi 25 ta được kết quả là bao nhiêu?
 Xem đáp án
Xem đáp án
Số các số hạng từ 1 đến 49 là:
(49 – 1) : 1 + 1 = 49 (số)
Tổng các số từ 1 đến 49 là:
(49 + 1) . 49 : 2 = 1225
Tổng của các số tự nhiên từ 1 đến 49 trừ đi 25 ta được:
1225 – 25 = 1200.
Đáp số: 1200.
Câu 38:
Một ô tô giờ thứ nhất chạy được 40km, giờ thứ hai chạy được nhiều hơn giờ thứ nhất 20km, quãng đường ô tô chạy được trong giờ thứ ba bằng trung bình cộng các quãng đường ô tô chạy được trong hai giờ đầu. Hỏi giờ thứ ba ô tô đó chạy được bao nhiêu km?
 Xem đáp án
Xem đáp án
Số ki–lô–mét ô tô chạy trong giờ thứ hai là:
40 + 20 = 60 (km).
Số ki–lô–mét ô tô chạy trong giờ thứ ba là:
(60 + 40) : 2 = 50 (km).
Đáp số: 50km.
Câu 39:
Một cửa hàng bán dầu, người ta chứa đầy dầu trong các thùng 20 lít. Nếu đổ số dầu đó vào các can 5 lít thì số can 5 lít nhiều hơn số thùng 20 lít là 30 cái. Hỏi cửa hàng đó có bao nhiêu lít dầu?
 Xem đáp án
Xem đáp án
20 lít so với 5 lít thì gấp một số lần là:
20 : 5 = 4 (lần)
Vì vậy số thùng 20 lít chỉ bằng số thùng 5 lít mà số thùng 5 lít nhiều hơn số thùng 20 lít là 30 cái, nên ta có sơ đồ:
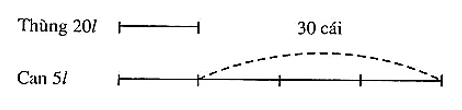
Số thùng 20 lít là:
30 : (4 – 1) = 10 (thùng)
Số lít dầu của cửa hàng là:
10 × 20 = 200 (lít).
Đáp số: 200 lít.
Câu 40:
Tìm số tự nhiên a lớn nhất, biết rằng 480 ⋮ a và 600 ⋮ a.
 Xem đáp án
Xem đáp án
Vì 480 ⋮ a và 600 ⋮ a nên a ∈ ƯC(480; 600)
Vì a là số tự nhiên lớn nhất nên a là ƯCLN của 480 và 600
Ta có: 480 = 25 . 3 . 5
600 = 23 . 3 . 52
ƯCLN(480; 600) = 23 . 3 . 5 = 120
Vậy a = 120.
Câu 41:
 Xem đáp án
Xem đáp án
Ta có: 144 = 24 . 32
192 = 26 . 3
⇒ ƯCLN(144, 192) = 24 . 3 = 48.
ƯC(144 ; 192) = Ư(48) = {1 ; 2 ; 3 ; 4 ; 6 ; 8 ; 12 ; 16 ; 24 ; 48}.
Trong các ước chung trên, ước chung lớn hơn 20 là: 24 ; 48.
Câu 42:
 Xem đáp án
Xem đáp án
420 ⋮ a và 700 ⋮ a nên a ∈ ƯC(420; 700).
a là số tự nhiên lớn nhất nên a = ƯCLN(420; 700).
Ta có:
420 = 22 . 3 . 5 . 7
700 = 22 . 52 . 7
⇒ ƯCLN(420, 700) = 22 . 5 . 7 = 140
Vậy a = 140.
Câu 43:
 Xem đáp án
Xem đáp án
Ta có: x + 21 = x + 3 + 18
Vì x + 3 chia hết cho x + 3 nên để x + 21 chia hết cho x + 3 thì 18 chia hết cho x + 3
Hay x + 3 ∈ Ư(18)
Suy ra: x + 3 ∈ {±1; ±2; ±3; ±6; ±9; ±18}
x ∈ {–2; –1 ; 0 ; 3 ; 6 ; 15 ; –4 ; –5 ; –6 ; –9 ; –12 ; –21}
Vậy x ∈ {–2; –1 ; 0 ; 3 ; 6 ; 15 ; –4 ; –5 ; –6 ; –9 ; –12 ; –21}.
Câu 44:
 Xem đáp án
Xem đáp án
Số các số hạng là:
(8789 – 8771) : 2 + 1 = 10 (số).
Tổng các số đó là:
(8789 + 8771) × 10 : 2 = 87800.
Câu 45:
Một tổ gồm 4 người trong 1 tuần trồng được 368 cây. Hỏi nếu tổ đó bổ sung thêm 3 người nữa thì trong 1 tuần tổ đó trồng được bao nhiêu cây? Biết mức trồng của mỗi người là như nhau.
 Xem đáp án
Xem đáp án
11 tuần = 7 ngày
1 người trong 1 ngày trồng được số cây là :
368 : 4 = 92 (cây)
Khi bổ sung thêm 3 người nữa thì tổng số người ở tổ đó là :
4 + 3 = 7 (người)
Trong 1 tuần cả tổ đó trồng được số cây là :
92 × 7 = 644 (cây)
Đáp số : 644 cây.
Câu 47:
Phân tích đa thức thành nhân tử: –25x6 – y8 + 10x3y4.
 Xem đáp án
Xem đáp án
–25x6 – y8 + 10x3y4
= – [(5x3)2 + (y4)2 – 10x3y4)
= – (5x3 – y4)2.
Câu 48:
Phân tích đa thức thành nhân tử: 2x2 – 12x + 18 + 2xy – 6y.
 Xem đáp án
Xem đáp án
2x2 – 12x + 18 + 2xy – 6y
= 2(x2 – 6x + 9) + 2y(x – 3)
= 2(x – 3)2 + 2y(x – 3)
= 2(x – 3)(x – 3 + y).
Câu 50:
 Xem đáp án
Xem đáp án
5x2 + 8xy + 5y2 = 72
9A = 9(x2 + y2) = 5x2 + 8xy + 5y2 + (4x2 – 8xy + 4y2)
9A = 72 + 4(x – y)2
Vì 4(x – y)2 ≥ 0 với mọi x, y nên 9A ≥ 72 hay A ≥ 8.
Suy ra giá trị nhỏ nhất của A là 8 khi x = y.
Khi đó ta có: 5x2 + 8x2 + 5x2 = 72
⇔ x2 = 4
⇔ x = ±2
Vậy giá trị nhỏ nhất của A là 8 khi x = y = ±2.
Câu 51:
 Xem đáp án
Xem đáp án
5x2 + 8xy + 5y2 = 72
9A = 9(x2 + y2) = 5x2 + 8xy + 5y2 + (4x2 – 8xy + 4y2)
9A = 72 + 4(x – y)2
Vì 4(x – y)2 ≥ 0 với mọi x, y nên 9A ≥ 72 hay A ≥ 8.
Suy ra giá trị nhỏ nhất của A là 8 khi x = y.
Khi đó ta có: 5x2 + 8x2 + 5x2 = 72
⇔ x2 = 4
⇔ x = ±2
Vậy giá trị nhỏ nhất của A là 8 khi x = y = ±2.
Câu 52:
Không tính kết quả, xét xem tổng (hiệu) sau là số nguyên tố hay hợp số ?
a) 15 + 3 . 40 + 8 . 9
b) 5 . 7 . 9 – 2 . 5 . 6
c) 90 . 17 – 34 . 40 + 12 . 51
d) 2010 + 4149
 Xem đáp án
Xem đáp án
a) 15 + 3 . 40 + 8 . 9 có các số hạng chia hết cho 3 và lớn hơn 3, nên nó chia hết cho 3 .
Vậy tổng đó là hợp số
b) 5.7.9 – 2.5.6 có các số hạng đều chia hết cho 5 và lớn hơn 5 , nên nó chia hết cho 5.
Vậy hiệu đó là hợp số..
c) 90.17 – 34.40 + 12.51 có các số hạng đều chia hết cho 17 và lớn hơn 17, nên nó chia hết cho 17
Vậy tổng đó là hợp số.
d) 2010 + 4149 có các số hạng chia hết cho 3 và lớn hơn 3, nên nó chia hết cho 3.
Vậy tổng đó là hợp số.
Câu 53:
Cho tam giác ABC vuông tại A có AC = 2AB. Vẽ tia phân giác Ax của A. Từ B vẽ đường thẳng vuông góc với Ax cắt AC tại F. Từ C vẽ đường thẳng vuông góc Ax cắt Ax tại E.
a) Chứng minh rằng: Tứ giác ABEF có bốn cạnh bằng nhau.
 Xem đáp án
Xem đáp án
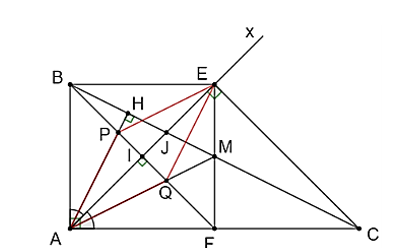
Lấy I là giao của Ax và BF.
a) AI là tia phân giác của góc BAF và AI cũng là đường cao của tam giác BAF nên
∆BAF cân tại A nên AB = AF.
Mà = 90°.
Khi đó ABEF là hình vuông.
Vậy ABEF có bốn cạnh bằng nhau.
Câu 54:
 Xem đáp án
Xem đáp án
b) Ta có: BE = AF = BA.
Mà AC = 2BA nên AC = 2AF và FC = AF = BE.
Lại có BE // AF và BE // FC.
Vậy BECF là hình bình hành.
Câu 55:
c) Vẽ trung tuyến AM và đường cao AH. BF cắt AH và AM tại P và Q. Hỏi APEQ là hình gì?
 Xem đáp án
Xem đáp án
c) Vì tứ giác ABEF là hình vuông nên I là trung điểm AE.
Xét ∆ABC vuông tại A có AM là trung tuyến
⇒ AM = MB = MC (tính chất trung tuyến tam giác vuông)
⇒ ∆AMC cân tại M
⇒
Mà (cùng phụ )
⇒=
Xét ∆ABP và ∆AFQ có:
AB = AF
(do ∆ABF cân tại A)
Do đó ∆ABP = ∆AFQ (g.c.g)
Suy ra AP = AQ (hai cạnh tương ứng).
Suy ra ∆APQ cân tại A, có AI là đường cao nên AI đồng thời là trung tuyến.
Do đó I là trung điểm PQ.
Xét tứ giác APEQ có: I là trung điểm AE và PQ.
Suy ra tứ giác APEQ là hình bình hành.
Lại có AE vuông góc PQ.
Vậy tứ giác APEQ là hình thoi.
Câu 56:
Chứng minh: n³ – 13n chia hết cho 6 (n thuộc ℤ).
 Xem đáp án
Xem đáp án
n³ –13n
= n (n² – 13)
= n (n² – 1 – 12)
= n [(n – 1)(n + 1) – 12]
= n(n – 1)(n + 1) – 12n
Ta thấy n (n – 1)(n + 1) là tích ba số tự nhiên liên tiếp nên có 1 thừa số chia hết cho 2 hay 3.
⇔ n (n – 1)(n + 1) chia hết cho 6
Mà 12n chia hết cho 6
⇒ n (n – 1)( n + 1) – 12n chia hết cho 6
Vậy n³ –13n chia hết cho 6.
Câu 57:
Có bao nhiêu số tự nhiên gồm 6 chữ số khác nhau đôi một trong đó có mặt chữ số 0 nhưng không có mặt chữ số 1?
 Xem đáp án
Xem đáp án
– Chọn vị trí cho số 0. Vì số 0 phải xuất hiện trong số đó nên ta chọn vị trí cho số 0 trước. Vì số 0 không được đứng ở vị trí đầu tiên nên ta có 5 vị trí để chọn cho số 0.
– Chọn các vị trí còn lại cho các số còn lại. Ta có 8 số còn lại để chọn (không có số 1), và ta phải chọn 5 số từ 8 số đó. Do đó, ta có cách chọn.
Vậy, số lượng số tự nhiên gồm 6 chữ số khác nhau đôi một trong đó có mặt chữ số 0 nhưng không có mặt chữ số 1 là: 5 .= 33600 (số)
Vậy có 33600 số thỏa mãn yêu cầu bài toán.
Câu 58:
Để lát nền một phòng học hình chữ nhật, người ta dùng loại gạch men hình vuông có cạnh 20cm. Hỏi cần bao nhiêu viên gạch để lát kín nền phòng học đó, biết rằng nền phòng học có chiều rộng 5m, chiều dài 8m và phần mạch vừa không đáng kể?
 Xem đáp án
Xem đáp án
Diện tích nền phòng học hình chữ nhật (không tính phần mạch vữa) là:
8 × 5 = 40 (m2)
Đổi 40 m2 = 400000 cm2
Diện tích của một viên gạch men hình vuông là:
20 × 20 = 400 (cm2)
Số viên gạch cần dùng là:
400000 : 400 = 1000 (viên)
Đáp số: 1000 viên gạch men.
Câu 59:
Một khu vườn hình chữ nhật có chu vi là 192m, chiều rộng bằng chiều dài.
a) Tính diện tích của khu vườn?
 Xem đáp án
Xem đáp án
a) Nửa chu vi hình chữ nhật là:
192 : 2 = 96 (m)
Chiều dài hình chữ nhật là:
96 : (3 + 5) . 5 = 60 (m)
Chiều rộng hình chữ nhật là:
96 – 60 = 36 (m)
Diện tích của mảnh vườn là:
36 × 60 = 2160 (m2)
Câu 60:
b) Người ta làm lối đi và đào ao thả cá trong phần đất hình chữ nhật có chiều dài 18m, chiều rộng 10m. Tính diện tích còn lại của khu vườn?
 Xem đáp án
Xem đáp án
b) Diện tích để làm lối đi và đào ao thả cá là:
18 × 10 = 180 (m2)
Diện tích còn lại là:
2160 – 180 = 1980 (m2).
Đáp số: a) 2160 m2; b) 1980 m2.
Câu 61:
Mảnh đất hình chữ nhật có chiều rộng bằng chiều dài. Biết rằng nếu giảm chiều dài 3m và tăng chiều rộng thêm 3 m thì mảnh đất có dạng hình vuông. Tính diện tích mảnh đất hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Chiều dài hơn chiều rộng là:
3 + 3 = 6 (m)
Chiều dài mảnh đất là:
6 : (4 – 3) × 4 = 24 (m).
Chiều rộng mảnh đất là:
24 – 6 = 18 (m).
Diện tích mảnh đất là:
24 × 18 = 378 (m2).
Đáp số: 378 m2.
Câu 62:
Người ta lát sàn một căn phòng hình chữ nhật có chiều dài 6m, chiều rộng 4m bằng những mảnh gỗ hình chữ nhật có chiều dài 1m 20cm, chiều rộng 20 cm. Hỏi cần bao nhiêu mảnh gỗ để lát kín sàn căn phòng đó?
 Xem đáp án
Xem đáp án
Đổi: 1m 20cm = 120cm.
Diện tích căn phòng đó là :
6 × 4 = 24 (m2) = 240000 (cm2)
Diện tích một mảnh gỗ hình chữ nhật là:
120 × 20 = 2400 (cm2)
Cần số mảnh gỗ để lát kín sàn căn phòng đó là:
240000 : 2400 = 100 (mảnh gỗ)
Đáp số: 100 mảnh gỗ.
Câu 63:
Người ta trồng ngô trên một khu đất có chu vi 130m, chiều dài bằng chiều rộng. biết rằng cứ 78 m2 đất thì trồng được 35 kg ngô. Hỏi mảnh đất đó trồng được bao nhiêu kg ngô?
 Xem đáp án
Xem đáp án
Nửa chu vi mảnh đất là:
130 : 2 = 65 (m)
Chiều dài mảnh đất là:
65 : (3 + 2) × 3 = 39 (m)
Chiều rộng mảnh đất là:
65 – 39 = 26 (m)
Diện tích mảnh đất là:
39 . 26 = 1014 (m2)
Mảnh đất đó trồng được số kg ngô là:
1014 : 78 . 35 = 455 (kg).
Đáp số: 455 kg ngô.
Câu 64:
Trung bình cộng của chiều dài và chiều rộng một mảnh đất là 28m, biết chiều dài của mảnh đất là 26m. Tính chu vi và diện tích của mảnh đất đó
 Xem đáp án
Xem đáp án
Tổng chiều dài và chiều rộng mảnh đất là:
28 × 2 = 56 (m)
Chiều rộng mảnh đất là:
56 – 26 = 30 (m)
Diện tích mảnh đất là:
30 × 26 = 780 (m2)
Chu vi mảnh đất là:
(30 + 26) × 2 = 112 (m).
Đáp số: diện tích: 780 m2; chu vi 112 mCâu 65:
Tìm số nguyên n bé nhất để F = n3 + 4n2 – 20n – 48 chia hết cho 125.
 Xem đáp án
Xem đáp án
F = n3 + 4n2 – 20n – 48
= n3 – 4n2 + 8n2 – 32n + 12n – 48
= (n – 4)n2 + 8n (n – 4) + 12(n – 4)
= (n – 4)(n2 + 8n + 12)
= (n – 4)(n + 2)(n + 6)
Vì (n – 4)(n + 2)(n + 6) chia hết cho 125, mà 125 chia hết cho 5 nên trong F tồn tại một thừa số chia hết cho 5
+ Nếu n + 2 chia hết cho 5 thì:
• n – 4 = n + 2 – 6, vì n + 2 chia hết cho 5, 6 không chia hết cho 5 nên n – 4 không chia hết cho 5
• n + 6 = n + 2 + 4, vì n + 2 chia hết cho 5, 4 không chia hết cho 5 nên n + 6 không chia hết cho 5
Do đó: Để F chia hết cho 125 thì n + 2 phải chia hết cho 125
⇒ n + 2 có giá trị bé nhất bằng 125 ⇒ n có giá trị bé nhất là 123
Tương tự ta xét tiếp hai trường hợp còn lại:
+ Nếu n – 4 chia hết cho 5 thì:
• n + 2 = n – 4 + 6 không chia hết cho 5
• n + 6 = n – 4 + 10 chia hết cho 5
Do đó: Để F chia hết cho 125 thì:
Hoặc n – 4 chia hết cho 25 và n + 6 chia hết cho 5
Hoặc n – 4 chia hết cho 5 và n + 6 chia hết cho 25
⇒ n bé nhất bằng 4
+ Nếu n + 6 chia hết cho 5 thì:
• n + 2 = n + 6 – 4 không chia hết cho 5
• n – 4 = n + 6 – 10 chia hết cho 5
Do đó: Để F chia hết cho 125 thì:
Hoặc n – 4 chia hết cho 25 và n + 6 chia hết cho 5
Hoặc n – 4 chia hết cho 5 và n + 6 chia hết cho 25
⇒ n bé nhất bằng 4.
Ta thấy qua ba trường hợp, 4 < 123 nên giá trị bé nhất của n để F chia hết cho 125 là n = 4
Vậy n = 4.
Câu 66:
Tìm số tự nhiên x biết rằng 720 chia hết cho x; 540 chia hết cho x và 70 < x < 100.
 Xem đáp án
Xem đáp án
720 ⋮ x; 540 ⋮ x
⇒ x ∈ ƯC(720; 540)
Ta có:
720 = 24 . 32 . 5
540 = 22 . 33 . 5
⇒ ƯCLN(720; 540) = 22 . 32 . 5 = 180
Ta có: ƯC(720; 540) = Ư(180)
⇒x ∈ Ư(180)
Vì 70 < x <180 nên x = 90
Vậy x = 90.
Câu 67:
Một lớp có 3 loại học sinh: Giỏi, Khá, Trung Bình. Biết số học sinh giỏi bằng số học sinh khá, số học sinh khá bằng 50% tổng số học sinh cả lớp. Còn lại là học sinh trung bình. Hỏi mỗi loại có bao nhiêu học sinh, biết lớp đó có 42 học sinh?
 Xem đáp án
Xem đáp án
Số học sinh khá là:
42 × 50% = 21 (học sinh)
Số học sinh giỏi là:
21 × = 7 (học sinh)
Số học sinh trung bình là:
42 – 21 – 7 = 14 (học sinh).
Câu 68:
 Xem đáp án
Xem đáp án
Gọi thời gian để hoàn thành công việc sau khi tăng thêm 15 người là x (0 < x < 12) (giờ)
Từ bài ra ta có số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.
Nếu tăng thêm 15 công nhân thì số công nhân sau khi tăng là:
45 + 15 = 60 (công nhân)
Theo bài ra ta có:
45 . 12 = 60 . x
⇒ 60x = 540
⇒ x = 9 (giờ)
Do đó thời gian hoàn thành công việc giảm đi 12 – 9 = 3 giờ
Câu 69:
 Xem đáp án
Xem đáp án
2x2 + 3y2 – xy – 3x – 5y – 4 = 0
⇔ 2x2 – (y + 3)x + 3y2 – 5y – 4 = 0 (*)
Đây là phương trình bậc hai ẩn x.
Ta có: ∆ = (y + 3)2 – 4 . 2(3y2 – 5y – 4) = – 23y2 + 46y + 41.
(*) có nghiệm khi ∆ ≥ 0 ⇔ – 23y2 + 46y + 41 ≥ 0 .
Khi đó (*) có nghiệm là .
Đặt y = t .
Vậy nghiệm của phương trình đã cho là với .
Câu 70:
Chứng minh rằng x3 + 3x2 + 2x chia hết cho 6.
 Xem đáp án
Xem đáp án
x3 + 3x2 + 2x = x (x2 + 3x + 2) = x(x + 1)(x + 2)
Vì x và x + 1 là 2 số nguyên liên tiếp nên x(x + 1)
Trường hợp 1: x = 3k (k ∈ ℤ)
⇒ x ⋮ 3
⇒ x(x + 1)(x + 2) ⋮ 3
Trường hợp 2: x = 3k + 1(k ∈ ℤ)
⇒ x + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1) ⋮ 3
Trường hợp 3: x = 3k + 2(k ∈ ℤ)
⇒ x + 1= (3k + 2) + 1 = 3k + 3= 3.(k + 1) ⋮ 3
Suy ra A ⋮ 3
Vậy A ⋮ 6.
Câu 71:
Một đơn vị bộ đội dự kiến 45 người để hoàn thành một công việc trong 14 ngày, sau đó để rút ngắn thời gian đơn vị đã điều động 70 người tham gia. Hỏi đơn vị hoàn thành công việc đó trong bao nhiêu ngày? (năng suất làm việc của mọi người như nhau).
 Xem đáp án
Xem đáp án
Nếu muốn làm xong công việc đó trong 1 ngày thì cần :
45 × 14 = 630 (người)
Cần số ngày để hoàn thành công việc là:
630 : 70 = 9 (ngày)
Đáp số: 9 ngày.
Câu 74:
 Xem đáp án
Xem đáp án
5x3 + 6x2 + 12x + 8 = 0
⇔ x3 + 6x2 + 12x + 8 = –4x3
⇔ (x + 2)3 = –4x3
⇔ (x + 2)3 = –x3 .
⇔ x + 2 = –x .
⇔ x = –2
⇔ x =
Câu 75:
Cho bốn số thực dương a, b, c, d thỏa mãn a3 + b3 + c3 = 3d3; b5 + c5 + d5 = 3a5 và c7 + d7 + a7 = 3b7. Chứng minh rằng a = b = c = d.
 Xem đáp án
Xem đáp án
Xét 4 trường hợp.
Trường hợp 1: a là số lớn nhất trong 4 số a, b, c, d
Từ b5 + c5 + d5 = 3a5 ⇒ a = b = c = d
Trường hợp 2: b là số lớn nhất trong 4 số a, b, c, d
Từ c7 + d7 + a7 = 3b7 ⇒ a = b = c = d
Trường hợp 3: c là số lớn nhất trong 4 số a, b, c, d
Từ a3 + b3 + c3 = 3d3 ≥ 3abc ⇒ d3 ≥ abc (1).
Từ b5 + c5 + d5 = 3a5 ≥ (2).
Từ c7 + d7 + a7 = 3b7 (3).
Từ (1), (2) và (3) suy ra abd ≥ c3, mà c lớn nhất nên a = b = c = d.
Trường hợp 4: d là số lớn nhất trong 4 số a, b, c, d
Từ a3 + b3 + c3 = 3d3 ⇒ a = b = c = d
Vậy ta có a = b = c = d.
Câu 76:
Cho các số từ 1 đến 9. Em hãy điền các số này vào các sô vuông, sao cho tổng của 3 ô hàng dọc, hàng ngang và đường chéo bằng nhau.
 Xem đáp án
Xem đáp án
Bước 1: Xác định tổng
- Tổng các số từ 1 đến 9 là: 1 + 2 +....+ 9 = 45
- Vì 3 ô cộng lại đều bằng nhau nên: Tổng 3 ô là 45 : 3 = 15
Bước 2: Lấy 15 : 3 = 5 suy ra ô trung tâm phải là 5
Bước 3: Chỉ cần nghĩ ra 2 số cộng lại bằng 10 (vì đều cộng với số 5): 10 = 1 + 9 = 2 + 8 = 3 + 7 = 4 + 6
Bước 4: Điền vào các ô theo cặp số.
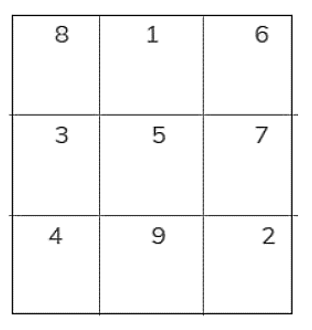
Câu 77:
Một kho chứa gạo lần đầu người ta lấy ra 32850kg, lần sau người ta lấy ra số gạo bằng lần đầu thì trong kho còn lại 26300kg gạo. Hỏi lúc đầu trong kho còn bao nhiêu tạ gạo?
 Xem đáp án
Xem đáp án
Lần sau người ta lấy ra số gạo là:
32850 : 3 = 10950 (kg)
Lúc đầu trong kho có số kg gạo là:
32850 + 10950 + 26300 = 70100 (kg)
Đổi 70100 kg = 701 tạ.
Câu 78:
Có bao nhiêu số có 4 chữ số chia hết cho 7 hoặc 17.
 Xem đáp án
Xem đáp án
Số lớn nhất có 4 chữ số chia hết cho 7 là 9996
Số bé nhất có 4 chữ số chia hết cho 7 là 1001
Số có 4 chữ số chia hết cho 7 là:
(9996 – 1001) : 7 + 1 = 1286 (số)
Số lớn nhất có 4 chữ số chia hết cho 17 là 9996
Số bé nhất có 4 chữ số chia hết cho 17 là 1003
Số có 4 chữ số chia hết cho 17 là:
(9996 – 1003) : 17 + 1 = 530 (số).
Câu 79:
Một mảnh đất hình chữ nhật có chiều dài 45m, chiều dài gấp 3 lần chiều rộng. Người ta dành 35% diện tích đất để làm nhà. Tính diện tích phần còn lại của mảnh đất đó.
 Xem đáp án
Xem đáp án
Chiều rộng mảnh đất là:
45 : 3 = 15 (m)
Diện tích mảnh đất là:
15 × 45 = 675 (m2).
Diện tích làm nhà là:
675 × 35% = 236,25 (m2).
Diện tích còn lại là:
675 – 236,25 = 438,75 (m2).
Đáp số: 438,75 m2.
Câu 80:
Miếng đất hình chữ nhật có chiều dài 45 m. Nếu mở rộng chiều dài thêm 7 m thì diên tích miếng đất tăng thêm 210 m2.
a) Tính diện tích miếng đất hình chữ nhật đó.
b) Người ta trồng bắp trên đất đó. Cứ 225 m2 thì thu được 5 tạ bắp. Tính số bắp thu hoạch được miếng đất đó.
 Xem đáp án
Xem đáp án
a) Chiều rộng của miếng đất là:
210: 7 = 30 (m)
Diện tích miếng đất đó là:
45 . 30 = 1350 (m2)
b) Số bắp thu hoạch được trên miếng đất đó là:
1350 : 225 . 5= 30 (tạ)
Câu 81:
a) Thay chữ số vào dấu * để được hợp số: 1* ; 3*
b) Thay chữ số vào dấu * để được số nguyên tố : 5* ; 9*
 Xem đáp án
Xem đáp án
a) 10; 12; 14; 15; 16; 18
30; 32; 33; 34; 35; 36; 38; 39
b) 51; 53; 59
91; 97
Câu 82:
Tìm số nguyên x và y sao cho 3xy + 2x – y = 0.
 Xem đáp án
Xem đáp án
3xy + 2x – y = 0
⇔ 9xy + 6x – 3y – 2 + 2 = 0
⇔3x (3y + 2) – (3y + 2) = –2
⇔ (3y + 2)(3x – 1) = – 2
Vì x, y là số nguyên nên ta có bảng:
|
3y + 2 |
2 |
–2 |
–1 |
1 |
|
3x – 1 |
–1 |
1 |
2 |
–2 |
|
y |
0 |
Loại |
–1 |
Loại |
|
x |
0 |
Loại |
1 |
Loại |
Vậy (x; y) ∈ {(1; –1); (0; 0)}.
