Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 25)
-
2071 lượt thi
-
95 câu hỏi
-
100 phút
Danh sách câu hỏi
Câu 1:
Hình chữ nhật có nửa chu vi là 99 m. Nếu tăng chiều rộng thêm 5 m và giảm chiều dài đi 5 m thì diện tích không thay đổi. Tính chiều dài và chiều rộng.
 Xem đáp án
Xem đáp án
Chiều dài hình chữ nhật là:
(99 + 5) : 2 = 52 (m)![]()
Chiều rộng hình chữ nhật là:
52 - 5 = 47 (m)
Đáp số: Chiều dài: 52 m;
Chiều rộng: 47 m.
Câu 2:
 Xem đáp án
Xem đáp án
Ta có: 158 : 2,8 = 56,42 (dư 0,24)
Vậy số dư của phép chia 158 : 2,8 là 0,24.
Câu 3:
 Xem đáp án
Xem đáp án
Đặt a = 4k; b = 4q (k, q Î ℕ*)
a + b = 48 Þ 4 (k + q) = 48
Þ k + q = 12
Mà (k, q) = 1 Þ (k, q) Î {(1, 11) ; (11, 1) ; (5, 7) ; (7, 5)}
Vậy (a, b) Î {(4, 44); (44, 4); (20, 28); (28, 20)}
Câu 4:
Tính diện tích hình thoi có chu vi 52 cm, một đường chéo bằng 24 cm
 Xem đáp án
Xem đáp án
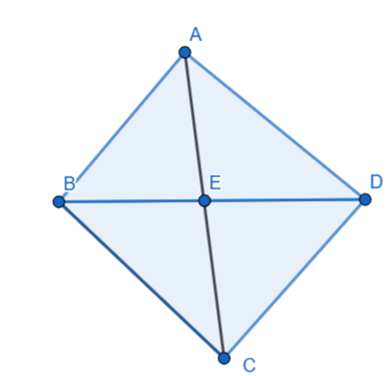
Độ dài mỗi cạnh của hình thoi là:
52 : 4 = 13 (cm)
Ta có: ED = EB nên ED = EB = (cm)
Theo định lý Py-ta-go cho tam giác AEB vuông, ta có:
AB2 = EB2 + EA2
Þ AE2 = AB2 - EB2 = 132 - 122 = 25
Þ AE = = 5 (cm)
Þ AC = 2AE = 10 (cm)
Þ SABCD = (cm2)
Câu 5:
Tính tổng: 1 + 3 + 5 + 7 + ... + (2n - 1).
 Xem đáp án
Xem đáp án
Khoảng cách giữa các dãy số bằng 2
Số hạng đầu dãy là 1
Số hạng cuối dãy là 2n - 1
Þ Số các số hạng là:
(2n - 1 - 1) : 2 + 1 = n
Þ Tổng các dãy số là:
[(1 + 2n - 1) . n] : 2
= 2n . n : 2 = n2.
Câu 6:
Tổng của hai số là 10,2. Nếu gấp số thứ nhất lên 3 lần và gấp số thứ hai lên 5 lần thì tổng của hai số là 41,4. Tìm hai số đó.
 Xem đáp án
Xem đáp án
Nếu cả hai số gấp lên 3 lần thì tổng của chúng là:
10,2 × 3 = 30,6
Số thứ hai là:
(41,4 - 30,6) : (5 - 3) = 5,4
Số thứ nhất là:
10,2 - 5,4 = 4.8
Câu 7:
Tìm x, biết:
a) x - 4 là bội của x - 1;
b) 2x - 1 là ước của 3x + 2.
 Xem đáp án
Xem đáp án
a) Ta có x - 4 chia hết cho x - 1
Þ (x - 1) - 3 chia hết cho x - 1
Þ 3 chia hết cho x - 1 (vì x - 1 chia hết cho x - 1)
Þ x - 1 Î Ư(3) = {-1; -3; 1; 3}
Ta có bảng giá trị
|
x - 1 |
-1 |
-3 |
1 |
3 |
|
x |
0 |
-2 |
2 |
4 |
Vậy x Î {0; -2; 2; 4}.
b) 2x - 1 là ước của 3x + 2
Û 3x + 2 là bội của 2x - 1
Þ 2(3x + 2) là bội của 2x - 1
Þ 6x + 4 là bội của 2x - 1
Þ 6x - 3 + 7 là bội của 2x - 1
Þ 3(2x - 1) + 7 chia hết cho 2x - 1
Mà 3(2x + 1) chia hết cho 2x - 1
Þ 7 chia hết cho (2x - 1)
Þ 2x - 1 Î Ư(7) = {-1; -7; 1; 7}
Ta có bảng giá trị:
|
2x - 1 |
-1 |
-7 |
1 |
7 |
|
2x |
0 |
-6 |
2 |
8 |
|
x |
0 |
-3 |
1 |
4 |
Vậy x Î {0; -3; 1; 4}.
Câu 8:
Cho parabol (P): y = x2 và đường thẳng (d): y = (2m - 1)x - m + 2 (m là tham số).
a) Chứng minh rằng với mỗi m, đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt
 Xem đáp án
Xem đáp án
a) Xét phương trình hoành độ giao điểm:
x2 = (2m - 1)x - m + 2 Û x2 - (2m - 1)x + m - 2 = 0
Ta có: D = (2m - 1)2 - 4(m - 2) = 4m2 - 8m + 9 = (2m - 1)2 + 8 ³ 8
Vậy nên phương trình luôn có hai nghiệm phân biệt tức hai đồ thị luôn cắt nhau tại 2 điểm phân biệt A và B
Câu 9:
b) Tìm các giá trị m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt A(x1; y1) ; B(x2; y2) thoả mãn x1y1 + x2y2 = 0.
 Xem đáp án
Xem đáp án
b) Theo định lý Viet:
Ta có: A(x1; y1) = A(x1; x12) và B(x2; y2) = B(x2; x22)
x1y1 + x2y2 = 0 Û x13 + x23 = 0
Û (x1 + x2)[(x1 + x2)2 - 3x1x2] = 0
Û (2m - 1)[(2m - 1)2 - 3m + 6] = 0
2m - 1 = 0 Û m =
(2m - 1)2 - 3m + 6 = 0 Û 4m2 - 7m - 7 = 0 (vô nghiệm)
Vậy m =
Câu 10:
Tính bằng cách thuận tiện nhất:
1 - 4 + 7 - 10 + 13 - 16 + ... + 103 - 106 + 109.
 Xem đáp án
Xem đáp án
1 - 4 + 7 - 10 + 13 - 16 + ... + 103 - 106 + 109
= (1 + 7 + 13 + ... + 103 + 109) - (4 + 10 + 16 + ... + 106)
= [(1 + 109) × 19 : 2] - [(106 + 4) × 18 : 2]
= 1045 - 990 = 55.
Câu 11:
Tính:
a) 1 - 2 - 3 + 4 + 5 - 6 - 7 + 8 + ... + 2001 - 2002 - 2003 + 2004
 Xem đáp án
Xem đáp án
a) 1 - 2 - 3 + 4 + 5 - 6 - 7 + 8 + ... + 2001 - 2002 - 2003 + 2004
S = (1 + 2 - 3 + 4) + (5 + 6 - 7 - 8) + ... + (2001 + 2002 - 2003 - 2004) + (2005 + 2006)
S = (-4) + (-4) + ... + (-4) + (2005 + 2006)
Dãy S có (2004 - 1) : 1 + 1 = 2004 (số hạng)
Dãy S có 2004 : 4 = 501 chữ số (-4)
Do đó S = (-4) . 501 = -2004
= -2004 + (2005 + 2006)
= -2004 + 4011 = 2007
Câu 12:
Tính:
b) 1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + 9 + ... + 2002 - 2003 - 2004 + 2005 + 2006
 Xem đáp án
Xem đáp án
b) 1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + 9 + ... + 2002 - 2003 - 2004 + 2005 + 2006
S = 1 + (2 - 3 - 4 + 5) + (6 - 7 - 8 + 9) + ... + (2002 - 2003 - 2004 + 2005) + 2006
S = 1 + 0 + 0 + ... + 0 + 2006 = 2007
Câu 13:
Điền số thích hợp vào chỗ chấm: 2, 3, 5, 6, 4, 7, 9, 12, 10, 12, 16, 18, 15, 19, 20...
 Xem đáp án
Xem đáp án
Trong mỗi dãy gồm bốn số, tổng của hai số ở giữa bằng tổng của số đầu với số cuối: 3 + 5 = 2 + 6, 4 + 12 = 7 + 9, 10 + 18 = 12 + 16.
Vậy số cần điền là: 19 + 20 - 15 = 24
Câu 16:
Tính: 367 + (-30) + 1672 + (-337).
 Xem đáp án
Xem đáp án
367 + (-30) + 1672 + (-337)
= (367 - 337) - 30 + 1672
= 330 - 30 + 1672
= 300 + 1672 = 1972
Câu 17:
Tính: 367 + (-30) + 2009 + (-337) + (-2010).
 Xem đáp án
Xem đáp án
367 + (-30) + 2009 + (-337) + (-2010)
= (367 - 337) - 30 + (2009 - 2010)
= 330 - 30 - 1
= 300 - 1 = 299
Câu 18:
Tính tổng: S = 1 - 3 + 5 - 7 + ... + 2001 - 2003
 Xem đáp án
Xem đáp án
S = 1 - 3 + 5 - 7 + ... + 2001 - 2003
S = (1 - 3) + (5 - 7) + ... + (2001 - 2003)
S = (-2) + (-2) + ... + (-2) (501 số hạng)
S = (-2) . 501
S = -1002
Vậy S = -1002
Câu 19:
 Xem đáp án
Xem đáp án
Áp dụng BĐT Cô-si cho 3 số dương:
Þ a + b + c ³ 3
Þ (a + b + c)3 ³ 27abc
Dấu "=" xảy ra khi a = b = c > 0
Vậy (a + b + c)3 ³ 27abc khi a = b = c > 0
Câu 20:
Tính nhanh: 37 . 444 - 144 . 111 + 15
 Xem đáp án
Xem đáp án
37 . 444 - 144 . 111 + 15
= 37 . 4 . 111 - 144 . 111 + 15
= 148 . 111 - 144 . 111 + 15
= 111 . (148 - 144) + 15 = 459
Câu 21:
Cho dãy số 1; 2; 3; 4; 5; ...; x. Tìm x để số của dãy gấp 4,5 lần x.
 Xem đáp án
Xem đáp án
Số chữ số trong các dãy có một chữ số là:
(9 - 1) .1 .1 = 9 (chữ số)
Số chữ số trong các dãy có hai chữ số là:
(90 - 10 + 1) . 2 = 180 (chữ số)
Số chữ số trong các dãy có ba chữ số là:
(999 - 100 + 1) . 3 = 2700 (chữ số)
Số chữ số trong các dãy có bốn chữ số là:
(9999 - 1000 + 1) . 4 = 36 000 (chữ số)
Ta có thể coi số chữ số có trong dãy số có 5 chữ số là: (x - 10 000 + 1) . 5
Theo đề bài, ta có:
(x - 10 000 + 1) . 5 + 9 + 180 + 2700 + 36 000 = x . 4,5
Þ x . 5 - 50 000 + 5 + 2889 + 36 000 = x . 4,5
Þ x . 0,5 = 6111
Þ x = 12 222
Vậy x = 12 222
Câu 22:
Cho hàm số y = mx + 3 (d). Tìm m để khoảng cách từ gốc toạ độ đến đường thẳng d lớn nhất
 Xem đáp án
Xem đáp án
Gọi A và B lần lượt là giao điểm của đường thẳng (d) với trục Ox, Oy.
Khi đó, , . Gọi H là hình chiếu của O lên đường thẳng (d) thì OH chính là khoảng cách từ điểm O tới đường thẳng (d)
Xét tam giác vuông OAB có:
Suy ra OHMAX Û
Ta có
mà
Vậy khoảng cách lớn nhất từ gốc toạ độ đến đường thẳng d bằng 3 khi và chỉ khi m = 0.
Câu 23:
Cho tam giác ABC có AB = AC. Gọi D là trung điểm của BC. Kẻ DE vuông góc với AB; DF vuông góc với AC. Chứng minh
a) DDEB = DDFC
 Xem đáp án
Xem đáp án
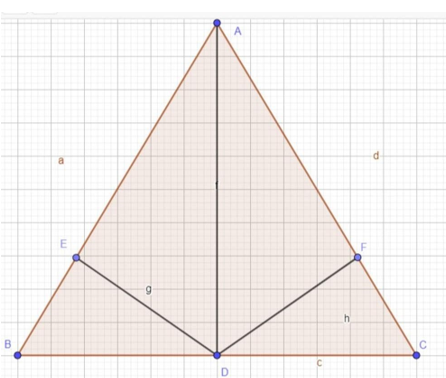
a) Xét DDEB và DDFC ta có:
(DE ^ AB; DF ^ AC)
BD = DC (vì D là trung điểm của BC)
(vì DABC cân tại A)
Þ DDEB = DDFC (cạnh huyền - góc nhọn)
Câu 24:
Chứng minh
b) DAED = DAFD
 Xem đáp án
Xem đáp án
b) Ta có: AE + EB = AB; AF + FC = AC
Mà EB = FC (vì DDEB = DDFC); AB = AC (vì DABC cân tại A)
Þ AE = AF
Xét DAED và DAFD ta có:
(DE ^ AB; DF ^ AC)
AD chung
AE = AF (cmt)
Do đó DAED = DAFD (cạnh huyền - cạnh góc vuông)
Câu 25:
Gọi A và B là hai điểm trên Ox sao cho OA = 4 cm, OB = 6 cm. Trên tia BA lấy điểm C sao cho BC = 4 cm.
a) Tính độ dài các đoạn thẳng AB và OC.
 Xem đáp án
Xem đáp án
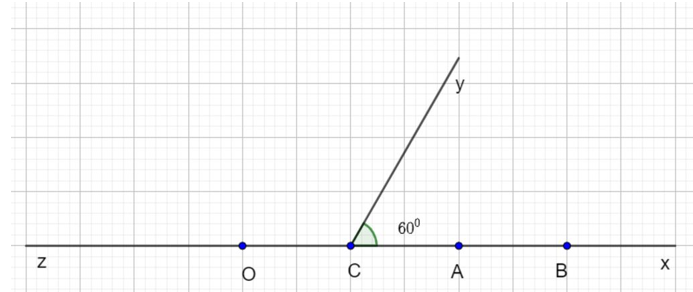
a) Nhìn vào hình vẽ, ta có:
OA + AB = OB Þ AB = OB - OA = 6 - 4 = 2 (cm)
OC + BC = OB Þ OC = OB - BC = 6 - 4 = 2 (cm)
Câu 26:
b) Điểm A có phải là trung điểm của đoạn thẳng BC không? Vì sao?
 Xem đáp án
Xem đáp án
b) Nhìn vào hình vẽ, ta có:
OC + AC = OA Þ AC = OA - OC = 4 - 2 = 2 (cm)
Mà AB = 2 cm nên AC = AB
Vì điểm A nằm giữa B và C; AB = AC
Vậy A là trung điểm của BC.
Câu 27:
c) Vẽ tia Cy sao cho và vẽ tia Cz là tia đối của tia Cx, chỉ ra các góc nhọn, góc tù, góc bẹt trong hình?
 Xem đáp án
Xem đáp án
c) Góc nhọn là góc xCy
Góc tù là góc zCy
Góc bẹt là góc xCz
Câu 28:
Một tấm bìa quảng cáo hình chữ nhật có chiều dài gấp 4 lần chiều rộng và diện tích bằng 1 m2. Phải dùng bao nhiêu mét nhôm để viền xung quanh tấm biển đó?
 Xem đáp án
Xem đáp án
Vì chiều dài gấp 4 lần chiều rộng nên chiều dài ứng với một phần thì chiều rộng ứng với 4 phần.
Theo bài ra, ta có hình chữ nhật gồm 4 ô vuông, chiều rộng một phần (ứng với cạnh của hình vuông), chiều dài ứng với 4 phần (4 lần cạnh hình vuông)
Diện tích 1 ô vuông là: 1 : 4 = 0,25 (cm2)
Vì 0,25 = 0,5 × 0,5 nên suy ra độ dài cạnh hình vuông (chiều rộng hình chữ nhật) là 0,5 m
Khi đó, chiều dài hình chữ nhật là: 0,5 × 4 = 2 (m)
Số mét nhôm cần dùng là: (2 + 0,5) × 2 = 5 (m)
Đáp số: 5 mét.
Câu 29:
 Xem đáp án
Xem đáp án
Chiều dài hình chữ nhật là:
8 × 3 = 24 (cm)
Diện tích hình chữ nhật là:
8 × 24 = 192 (cm2)
Chu vi hình chữ nhật là:
(24 + 8) × 2 = 64 (cm)
Đáp số: Diện tích là 192 cm2
Chu vi là 64 cm
Câu 30:
Một mảnh đất hình chữ nhật có chiều dài 36 m, chiều rộng bằng chiều dài. Hãy tính diện tích mảnh đất đó ?
 Xem đáp án
Xem đáp án
Chiều rộng của mảnh đất hình chữ nhật đó là:
36 : 4 = 9 (m)
Diện tích của mảnh đất hình chữ nhật đó là:
36 × 9 = 324 (m2)
Đáp số: 324 m2.
Câu 31:
Người ta xếp 187 250 cái áo vào các hộp, mỗi hộp 8 áo. Hỏi có thể xếp được vào nhiều nhất bao nhiêu hộp và còn thừa mấy cái áo?
 Xem đáp án
Xem đáp án
Ta có: 187 250 : 8 = 23 406 (dư 2)
Vậy ta có thể xếp được vào nhiều nhất 23 406 hộp và còn thừa 2 cái áo
Đáp số: 23 406 hộp và còn thừa 2 cái áo
Câu 32:
Người ta đổ đều 128 610 lít xăng vào 6 bể. Hỏi mỗi bể đó có bao nhiêu lít xăng?
 Xem đáp án
Xem đáp án
Số lít xăng ở mỗi bể là:
128 610 : 6 = 21 435 (l)
Đáp số: 21 435 lít.
Câu 33:
Bố hơn con 30 tuổi, biết 5 năm nữa tổng số tuổi của hai bố con là 62 tuổi. Tính tuổi 2 bố con hiện nay.
 Xem đáp án
Xem đáp án
Tuổi bố 5 năm trước là:
(62 + 30) : 2 = 46 (tuổi)
Tuổi con 5 năm trước là:
62 - 46 = 16 (tuổi)
Tuổi bố hiện nay là:
46 + 5 = 51 (tuổi)
Tuổi con hiện nay là:
16 + 5 = 21 (tuổi)
Đáp số: Tuổi bố: 51 tuổi;
Tuổi con: 21 tuổi.
Câu 34:
Bố năm nay 30 tuổi sau 5 năm nữa tuổi bố gấp 5 lần tuổi con. Hỏi năm nay con bao nhiêu tuổi?
 Xem đáp án
Xem đáp án
Lời giải:
Tuổi bố sau 5 năm nữa là:
30 + 5 = 35 (tuổi)
Tuổi con sau 5 năm nữa là:
35 : 5 = 7 (tuổi)
Tuổi con bây giờ là:
7 - 5 = 2 (tuổi)
Đáp số: 2 tuổi.
Câu 35:
Tìm số dư của phép chia 218 : 3,7 nếu chỉ lấy đến hai chữ số ở phần thập phân của thương.
 Xem đáp án
Xem đáp án
Lời giải:
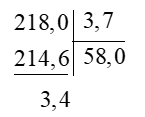
Vậy số dư của phép chia 218 : 3,7 là 3,40.
Câu 36:
Thùng to có 21 l dầu, thùng bé có 15 l dầu. Số dầu đó được chứa vào các chai như nhau, mỗi chai có 0,75 l. Hỏi tất cả bao nhiêu chai dầu ?
 Xem đáp án
Xem đáp án
Tổng số lít dầu của cả hai thùng là:
21 + 15 = 36 (l)
Có tất cả số chai dầu là:
36 : 0,75 = 48 (chai)
Đáp số : 48 chai dầuCâu 37:
Trên tia Ox lấy 2 điểm M và N sao cho OM = 3 cm và ON = 7 cm
a) Tính độ dài đoạn thẳng MN
 Xem đáp án
Xem đáp án
a)
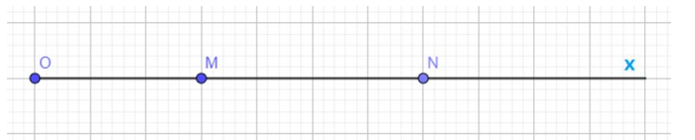
Ta có : OM + MN = ON
Þ MN = ON - OM = 7 - 3 = 4 (cm)
Vậy MN = 4 cm
Câu 38:
b) Lấy P trên tia Ox sao cho MP = 2 cm. Tính độ dài đoạn thẳng OP.
 Xem đáp án
Xem đáp án
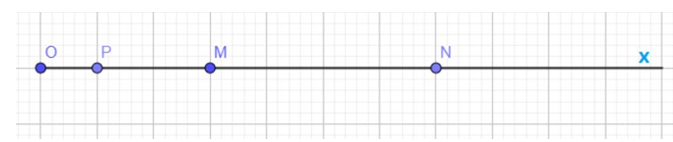
Trường hợp 1: P nằm giữa M và O
Ta có: OP + PM = OM
Þ OP = OM - PM = 3 - 2 = 1 (cm)
Vậy OP = 1 cm
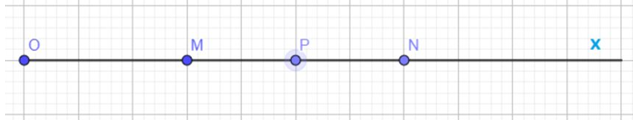
Trường hợp 2: M nằm giữa O và P
Ta có: OM + MP = OP
Þ OP = OM + MP = 3 + 2 = 5 (cm)
Vậy OP = 5 cm
Câu 39:
c) Trong trường hợp M nằm giữa O và P. Chứng tỏ P là trung điểm đoạn thẳng MN.
 Xem đáp án
Xem đáp án
c) Theo trường hợp 2 ta có:
MN - MP = PN
Þ PN = MN - MP = 4 - 2 = 2 (cm)
vì MP = PN = = 2 (cm)
nên P là trung điểm MN (đpcm)
Câu 41:
Tìm tỉ số phần trăm của 2 và và 3 và .
 Xem đáp án
Xem đáp án
Tỉ số phần trăm của 2 và là:
2 : × 100 = 266,6%
Tỉ số phần trăm của 3 và là:
3 : × 100 = 525%
Vậy tỉ số phần trăm của 2 và là 266,6%; tỉ số phần trăm của 3 và là 525%.
Câu 42:
 Xem đáp án
Xem đáp án
Ta có: Gấp thừa số thứ nhất lên 2 lần, thừa số thứ hai lên 4 lần đồng nghĩa với việc thừa số sẽ được gấp lên 2 lần và 4 lần.
Vậy, tích mới của 2 số là:
34,6 × 2 × 4 = 276,8
Đáp số: 276,8
Câu 43:
Tính nhanh: 20,14 × 6,8 + 20,14 × 3,2.
 Xem đáp án
Xem đáp án
20,14 × 6,8 + 20,14 × 3,2
= 20,14 × (6,8 + 3,2)
= 20,14 × 10 = 201,4.
Câu 44:
Đơn giản biểu thức sau khi bỏ ngoặc:
a) (a + b - c) - (b - c + d);
b) -(a - b + c) + (a - b + d);
c) (a + b) - (-a + b - c);
 Xem đáp án
Xem đáp án
a) (a + b - c) - (b - c + d)
= a + b - c - b + c - d
= a + (b - b) + (-c + c) - d
= a - d
b) -(a - b + c) + (a - b + d)
= -a + b - c + a - b + d
= (a - a) + (b - b) - c + d
= d - c.
c) (a + b) - (-a + b - c)
= a + b + a - b + c
= (a + a) + (b - b) + c
= 2a + c.
Câu 45:
Đơn giản biểu thức sau khi bỏ ngoặc:
d) -(a + b) + (a + b + c);
e) (a - b + c) - (a - b + c);
f) -(a - b - c) + (a - b - c).
 Xem đáp án
Xem đáp án
d) -(a + b) + (a + b + c)
= -a - b + a + b + c
= (-a + a) + (-b + b) + c = c.
e) (a - b + c) - (a - b + c)
= a - b + c - a + b - c
= (a - a) + (-b + b) + (c - c) = 0.
f) -(a - b - c) + (a - b - c)
= -a + b + c + a - b - c
= (-a + a) + (b - b) + (c - c) = 0.
Câu 46:
Tính hợp lý : (-2020) - 2018 - 2016 - ... - 2008.
 Xem đáp án
Xem đáp án
(-2020) - 2018 - 2016 - ... - 2008
= -(2008 + ... + 2016 + 2018 + 2020)
= {(2020 . 2008) . [(2020 - 2018) : 2 + 1] : 2}
= -(4028 . 7 : 2)
= -(2014 . 7)
= -14098
Câu 47:
Cho hàm số y = (5 - 2m)x + 3.
a) Tìm m để hàm số là hàm số bậc nhất. Xem đáp án
Xem đáp án
a) Hàm số bậc nhất khi 5 - 2m ≠ 0 Û m ≠
b) Hàm số nghịch biến khi 5 - 2m < 0 Û 2m > 5
Û m >
Câu 48:
c) Vẽ đồ thị hàm số với m = 1.
 Xem đáp án
Xem đáp án
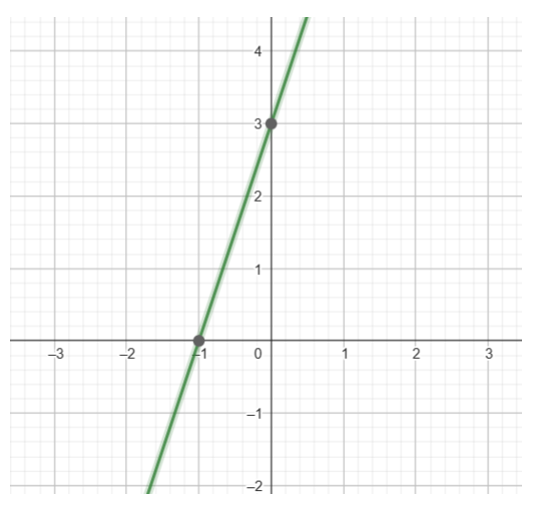
c) Với m = 1 hàm số trở thành y = (5 - 2.1)x + 3
Û y = 3x + 3
+) Cho x = 0 Þ y = 3 Þ (0; 3) thuộc Oy.
+) Cho y = 0 Þ x = -1 Þ (-1; 0) thuộc Ox.
Do đó, đồ thị hàm số y = 3x + 3 là đường thẳng đi qua hai điểm (0; 3) và (-1; 0).
Câu 49:
 Xem đáp án
Xem đáp án
Gọi số đó là A (A Î ℕ*)
Vì A chia cho 5 dư 1, chia cho 7 dư 5 nên ta có:
A = 5k + 1 = 7h + 5 ("k, h Î ℕ*)
Þ A + 9 = 5k + 1 + 9 = 5k + 10 = 5.(k + 2)
A + 9 = 7h + 5 + 9 = 7h + 14 = 7.(h + 2)
Þ A + 9 chia hết cho 5 và 7
Þ A + 9 là BCNN(5, 7)
Mà ƯCLN(5, 7) = 1 nên BCNN(5, 7) = 5 . 7 = 35
Þ A + 9 = 35
Þ A = 35 - 9 = 26
Vậy số cần tìm là 26
Câu 50:
Tìm số tự nhiên có hai chữ số, biết rằng nếu viết thêm chữ số 0 vào giữa chữ số hàng chục và hàng đơn vị của nó ta được 1 số gấp 7 lần số đó
 Xem đáp án
Xem đáp án
Ta có số cũ dạng , số mới
Ta có: a . 100 + b = (a . 10 + b) . 7
a . 100 + b = a . 70 + b . 7
a . 30 = b . 6 Þ a . 5 = b . 1
Vậy số đó là 15
Câu 51:
Một thửa ruộng hình chữ nhật có chu vi 96 m, chiều rộng ngắn hơn chiều dài 30 m. Tính diện tích của thửa ruộng ?
 Xem đáp án
Xem đáp án
Nửa chu vi thửa ruộng đó là:
96 : 2 = 48 (m)
Chiều dài thửa ruộng đó là:
(48 + 30) : 2 = 39 (m)
Chiều rộng thửa ruộng đó là:
48 - 39 = 9 (m)
Diện tích thửa ruộng đó là:
39 × 9 = 351 (m2)
Đáp số: 351 m2.
Câu 52:
Cho dãy số tự nhiên liên tiếp từ 1 đến n. Tìm n biết rằng tổng các số hạng đó bằng 190.
 Xem đáp án
Xem đáp án
Số số hạng của dãy số tự nhiên liên tiếp từ 1 đến n là n.
Tổng của các dãy số đó là: (n + 1) × n : 2
Có: (n + 1) × n : 2 = 190
(n + 1) × n = 190 × 2 = 380 = 19 × 20
Suy ra n = 19.
Câu 53:
Đâu là cạnh kề cạnh đối cạnh huyền trên tam giác vuông
 Xem đáp án
Xem đáp án
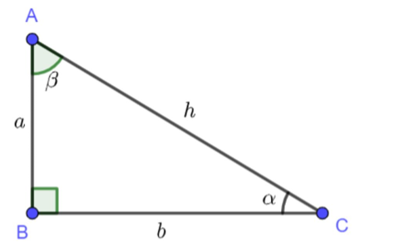
Giả sử ta có tam giác vuông như hình vẽ
Với góc a < 90° ta có b là cạnh kề, a là cạnh đối, h là cạnh huyền.
Với góc b < 90° ta có a là cạnh kề, b là cạnh đối, h là cạnh huyền.
Tóm lại :
Cạnh huyền là cạnh đối diện góc vuông,
Cạnh kề là cạnh góc vuông kề với góc đó,
Cạnh đối là cạnh góc vuông đối diện với góc đó
Câu 54:
Cho hàm số y = f(x) có đạo hàm y = = x(x - 2)3, với mọi x Î ℝ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hàm số nghịch biến
Û
Suy ra hàm số y = f(x) nghịch biến trên khoảng (0; 2)
Câu 55:
Cho tam giác ABC, trọng tâm G.
a) Vẽ đường thẳng d qua G, cắt các đoạn thẳng AB, AC. Gọi A', B', C' là hình chiếu của A, B, C trên d. Tìm liên hệ giữa các độ dài AA', BB', CC'
 Xem đáp án
Xem đáp án
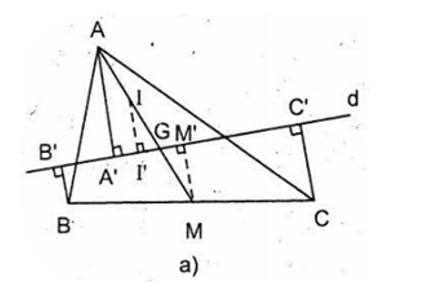
a) (Hình a) Lấy điểm I trên đường trung tuyến AM sao cho I là trung điểm của AG. Kẻ AA', BB', CC', II', MM' vuông góc với d.
Đáp số: AA' = BB' + CC'
Câu 56:
b) Nếu đường thẳng d nằm ngoài tam giác ABC và G' là hình chiếu của G trên d thì các độ dài AA', BB', CC', GG' có liên hệ gì ?
 Xem đáp án
Xem đáp án

b) (Hình b) Gọi BE là đường trung tuyến của AC, M là trung điểm của BG. Vẽ AA', BB', CC', II', MM' vuông góc với d.
Ta có: MM' + EE' = 2GG'
Þ 2MM' + 2EE' = 4GG'
Þ BB' + GG' + AA' + CC' = 4GG'
Þ AA' + BB' + CC' = 3GG'
Câu 57:
Hai bạn Tùng và Hải thường đến thư viện đọc sách. Tùng cứ 8 ngày đến thư viện 1 lần, Hải cứ 10 ngày 1 lần. Lần đầu cả hai bạn cùng đến thư viện vào một ngày. Hỏi sau ít nhất bao nhiêu ngày thì hai bạn cùng đến thư viện?
 Xem đáp án
Xem đáp án
Gọi sau ít nhất m ngày thì hai bạn cùng đến thư viện (m Î ℕ*)
Vì số ngày ít nhất nên m là BCNN(8, 10)
Ta có: 8 = 23; 10 = 2 . 5.
BCNN(8, 10) = 23 . 5 = 40.
Vậy sau 40 ngày thì hai bạn cùng nhau đến thư viện.
Câu 58:
Một cửa hàng trong một ngày bán được 3 tạ rưỡi gạo. Buổi sáng bán được 1 tạ rưỡi gạo, buổi chiều bán kém buổi tối là 60 kg. Hỏi buổi chiều và buổi tối, mỗi buổi bán được bao nhiêu tạ gạo ?
 Xem đáp án
Xem đáp án
Đổi 3 tạ rưỡi = 350 kg
1 tạ rưỡi = 150 kg
Buổi chiều và buổi tối bán được số gạo là:
350 - 150 = 200 (kg)
Buổi chiều bán được số gạo là:
(200 - 60) : 2 = 70 (kg)
Buổi tối bán được số gạo là:
200 - 70 = 130 (kg)
Đổi 70 kg = 0,7 tạ
130 kg = 1,3 tạ
Câu 59:
Tìm các số x, y, z biết 2x = 3y, 5y = 7z và 3x - 7y + 5z = 30.
 Xem đáp án
Xem đáp án
2x = 3y Þ (1)
(2)
Từ (1) và (2) suy ra .
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Khi đó:
•
•
•
Vậy x = 42, y = 28, z = 20.
Câu 60:
 Xem đáp án
Xem đáp án
Xét tam giác ABE có: AB // DG (do AB // CD)
Áp dụng định lý Ta-lét, ta có:
Mà DE + EB = DB
Þ DE = DB
Þ
Câu 61:
Cho nửa đường tròn (O) đường kính AB, kẻ tiếp tuyến Ax. Qua C nằm trên đường tròn kẻ tiếp tuyến với nửa đường tròn cắt Ax tại M, tia Bx cắt Ax tại N.
a) Chứng minh OM vuông góc với AC.
 Xem đáp án
Xem đáp án
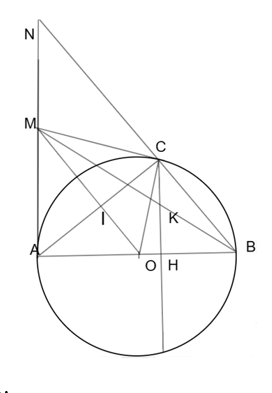
a) Xét DMAO và DMCO có:
MA = MC
MO: chung
AO = AC
Do đó DMAO = DMCO (c.c.c).
Suy ra (hai góc tương ứng).
Nên OM là phân giác mà tam giác AOC cân tại O.
Do đó OM là đường cao của DAOC.
Vậy OM ^ AC.
Câu 62:
 Xem đáp án
Xem đáp án
b) Từ câu a ta suy ra được OM vừa là đường cao vừa là đường trung tuyến
Nên OM ^ AC mà NC ^ AC
Suy ra OM // NC (1)
Ta lại có: AI = IC (2)
Từ (1) và (2) suy ra OM là đường trung bình của DONC.
Vậy M là trung điểm của AN.
Câu 63:
c) Kẻ CH vuông góc AB, BM cắt CH ở K. Chứng minh K là trung điểm của CH.
 Xem đáp án
Xem đáp án
c) Ta thấy rằng CH // AN (vì cùng vuông góc AB)
Suy ra .
Mà MN = AM nên CK = KH.
Vậy K là trung điểm của CH.
Câu 64:
 Xem đáp án
Xem đáp án
2cos2(x) + 3sin2(x) = 2
Û 2cos2(x) + 2sin2(x) + sin2(x) = 2 (do sin2(x) + cos2(x) = 1)
Û 2 + sin2(x) = 2
Û sin2(x) = 0
Û sin(x) = 0
Û x = kp (k Î ℤ)
Vậy phương trình đã cho có nghiệm x = kp (k Î ℤ)
Câu 65:
Cho 10k - 1 chia hết cho 19 với k > 1. Chứng minh rằng:
a) 102k - 1 chia hết cho 19.
 Xem đáp án
Xem đáp án
a) 102k - 1 = (10k)2 - 12 ⋮ (10k - 1)
Mà 10k - 1 ⋮ 19
Þ 102k - 1 ⋮ 19
Câu 66:
Cho 10k - 1 chia hết cho 19 với k > 1. Chứng minh rằng:
b) 103k - 1 chia hết cho 19.
 Xem đáp án
Xem đáp án
b) 103k - 1 = (10k)3 - 13 ⋮ (10k - 1)
mà 10k - 1 ⋮ 19
Þ 103k - 1 ⋮ 19
Câu 67:
Cách đây 4 năm tuổi bố gấp 5 lần tuổi con. Tính tuổi của mỗi người hiện nay biết rằng bố hơn có 28 tuổi.
 Xem đáp án
Xem đáp án
Ta có sơ đồ:
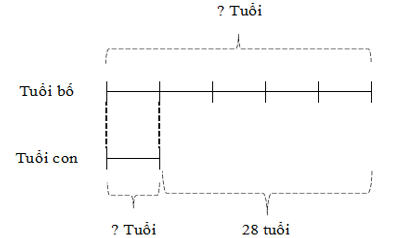
Theo sơ đồ, hiệu số phần bằng nhau là:
5 - 1 = 4 (phần)
Tuổi của bố là:
(28 : 4) . 5 + 4 = 39 (tuổi)
Tuổi của con là:
39 - 28 = 11 (tuổi)
Đáp số: Tuổi bố: 39 tuổi;
Tuổi con: 11 tuổi.
Câu 68:
 Xem đáp án
Xem đáp án
x3 + 2x - 3 = x3 - x2 + x2 - x + 3x - 3
= x2(x - 1) + x(x - 1) + 3(x - 1)
= (x - 1)(x2 + x + 3)
Câu 69:
Cho góc tù a có sina =
a) Tính cosa, tana, cota
 Xem đáp án
Xem đáp án
a) Vì a là góc tù (90° < a < 180°) nên cosa < 0
Ta có: sin2a + cos2a = 1
Þ
(do cosa < 0)
Do đó: tana =
Vậy cosa = ; tana = và cota =
Câu 70:
Phân tích đa thức thành nhân tử: x3 - 10x2 + 25x.
 Xem đáp án
Xem đáp án
x3 - 10x2 + 25x
= x(x2 - 10x + 25)
= x(x2 - 2 . x . 5 + 52)
= x(x - 5)2
Câu 71:
Cho a ³ 3, b ³ 4, c ³ 2. Tìm giá trị lớn nhất của biểu thức:
.
 Xem đáp án
Xem đáp án
Vì a ³ 3, b ³ 4 và c ³ 2, ta có:
• ;
• ;
• .
Do đó
Mà
Vậy giá trị lớn nhất là .
Vậy giá trị lớn nhất là khi a = 3, b = 4, c = 2.
Câu 72:
Một khu đất hình chữ nhật có chiều dài hơn chiều rộng 35 m. Nếu mỗi chiều tăng thêm 5 m thì diện tích tăng thêm 1450 m2. Hỏi khu đất đó có diện tích là bao nhiêu héc-ta?
 Xem đáp án
Xem đáp án
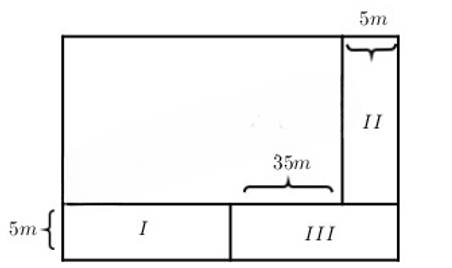
Theo đề bài ta có hình vẽ:
Chia phần tăng thêm thành ba hình chữ nhật như hình vẽ
Hình III có chiều rộng là 5 m, chiều dài là: 35 + 5 = 40 (m)
Diện tích hình III là:
40 × 5 = 200 (m2)
Hình I và hình II vì đều có chiều rộng bằng 5 m và chiều dài bằng chiều rộng cũ của khu đất
Tổng diện tích khu đất hình I và hình II là:
1450 - 200 = 1250 (m2)
Diện tích hình I hay hình II là:
1250 : 2 = 625 (m2)
Chiều rộng của khu đất là:
625 : 5 = 125 (m)
Chiều dài của khu đất là:
125 + 35 = 160 (m)
Diện tích của khu đất là:
160 × 125 = 20 000 (m2)
Đổi: 20 000 m2 = 2 ha
Đáp số: 2 ha
Câu 74:
Giải phương trình: 18 + 3(x - 2) = 63
 Xem đáp án
Xem đáp án
18 + 3(x - 2) = 63
Û 3(x - 2) = 63 - 18
Û 3(x - 2) = 45
Û x - 2 = 45 : 3
Û x - 2 = 15
Û x = 15 + 2
Û x = 17
Vậy nghiệm của phương trình đã cho là x = 17.
Câu 75:
Cô giáo đem chia một số kẹo cho các em. Cô nhẩm tính, nếu chia cho mỗi em 5 chiếc thì thừa 3 chiếc, nếu chia cho mỗi em 6 chiếc thì thiếu 5 chiếc. Hỏi cô giáo có bao nhiêu cái kẹo ?
 Xem đáp án
Xem đáp án
Số kẹo đủ để chia cho mỗi bạn 6 chiếc nhiều hơn số kẹo đủ để chia cho mỗi bạn 5 chiếc là:
3 + 5 = 8 (chiếc)
Số kẹo mỗi bạn được chia 6 chiếc nhiều hơn số kẹo mỗi bạn được chia 5 chiếc là:
6 - 5 = 1 (chiếc)
Số bạn có tất cả là:
8 : 1 = 8 (bạn)
Số kẹo có tất cả là:
8 × 5 + 3 = 43 (chiếc)
Đáp số: 43 chiếc kẹo
Câu 76:
Chứng minh rằng không có số tự nhiên nào chia cho 15 dư 6 và chia 9 dư 1
 Xem đáp án
Xem đáp án
Giả sử số tự nhiên chia hết cho 15 dư 6 và chia 9 dư 1 là A
Do A chia hết cho 15 dư 6 suy ra A = 15m + 6 (m là số tự nhiên bất kì)
A chia hết cho 9 dư 1 suy ra A = 9n + 1 (n là số tự nhiên bất kì)
Þ 15m + 6 = 9n + 1
Þ 9n - 15m = 6 - 1 (Quy tắc chuyển vế)
Þ 9n - 15m = 5
Ta lại có: (theo tính chất chia hết của một hiệu)
Khi đó 5 phải chia hết cho 3 (Vô lí)
Vậy không tồn tại số tự nhiên nào thoả mãn điều kiện chia hết cho 15 dư 6 và chia 9 dư 1
Câu 77:
 Xem đáp án
Xem đáp án
Ta có bất đẳng thức Bunhiacopski: (a2 + b2)(x2 + y2) ³ (ax + by)2
Dấu "=" xảy ra khi
(1)
(2)
Trừ từng vế của hai bất đẳng thức (1) và (2), ta được:
Û (a10 + b10)(a2 + b2) - (a8 + b8)(a4 + b4) ³ 0
Û (a10 + b10)(a2 + b2) ³ (a8 + b8)(a4 + b4)
Dấu "=" xảy ra khi a = b.
Câu 78:
 Xem đáp án
Xem đáp án
Anh hơn em số tuổi là:
13 - 3 = 10 (tuổi)
Vì mỗi năm mỗi người tăng thêm một tuổi nên anh luôn luôn hơn em 10 tuổi.
Số tuổi của anh gấp 3 lần số tuổi của em nên ta có sơ đồ hiệu tỉ

Theo sơ đồ, hiệu số phần bằng nhau là:
3 - 1 = 2 (phần)
Khi tuổi anh gấp 3 lần tuổi em thì khi đó tuổi em là:
10 : 2 = 5 (tuổi)
Vậy sau số năm tuổi anh gấp 3 lần tuổi em là:
5 - 3 = 2 (năm)
Đáp án: 2 năm
Câu 79:
Lớp 5A có số học sinh nam nhiều hơn số học sinh nữ là 4 học sinh. Biết số học sinh nữ bằng số học sinh nam. Hỏi lớp 5A có bao nhiêu học sinh nam, bao nhiêu học sinh nữ ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có sơ đồ:
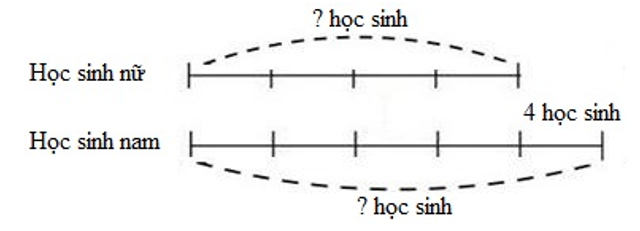
Theo sơ đồ, hiệu số phần bằng nhau là:
5 - 4 = 1 (phần)
Lớp 5A có số học sinh nữ là:
4 : 1 × 4 = 16 (học sinh)
Lớp 5A có số học sinh nam là:
16 + 4 = 20 (học sinh)
Đáp số: 16 học sinh nữ; 20 học sinh nam
Câu 80:
Một vườn trẻ dự trữ gạo cho 120 em bé ăn trong 20 ngày. Sau đó có thêm một số em bé mới đến nên số ngày ăn giảm đi 4 ngày. Hỏi có bao nhiêu em bé mới đến thêm ?
 Xem đáp án
Xem đáp án
Để ăn hết số gạo đó trong 1 ngày cần số em là:
120 × 20 = 2400 (em)
Số gạo còn ăn được trong số ngày nữa là:
20 - 4 = 16 (ngày)
Số em đến thêm là:
(2400 : 16) - 120 = 30 (em)
Đáp số: 30 em.
Câu 81:
Tìm số tự nhiên nhỏ nhất chia cho 5, 7, 9 có số dư lần lượt là 3, 4, 5.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là a
Giả sử a : 5 được b dư 3
Þ a = 5b + 3
Þ 2a = 10b + 6 = 10b + 5 + 1
Û 2a - 1 = 10b + 5 hay (2a - 1) ⋮ 5 (1)
Giả sử a : 7 được c dư 4
Þ a = 7c + 4
Þ 2a = 14c + 8 = 14c + 7 + 1
Þ 2a - 1 = 14c + 7 hay (2a - 1) ⋮ 7 (2)
Giả sử a : 9 được d dư 5
Þ a = 9d + 5
Þ 2a = 18d + 10 = 18d + 9 + 1
Þ 2a - 1 = 18d + 9 hay (2a - 1) ⋮ 9 (3)
Từ (1), (2), (3) suy ra (2a - 1) chia hết cho 5, 7 và 9.
Vì đề yêu cầu tìm số tự nhiên nhỏ nhất nên ta tìm bội chung nhỏ nhất của 5, 7, 9.
BCNN(5, 7, 9) = 5 . 7 . 9 = 315
Þ 2a - 1 = 315
Þ 2a = 316
Þ a = 158
Vậy số cần tìm là 158.
Câu 82:
Trước đây mua 5m vải phải trả 60 000 đồng. Hiện nay giá bán mỗi mét vải đã giảm 2000 đồng. Hỏi với 60 000 đồng, hiện nay có thể mua được bao nhiêu mét vải như thế?
 Xem đáp án
Xem đáp án
Trước đây giá 1 m vải là:
60 000 : 5 = 12 000 (đồng)
Hiện nay, giá 1 m vải là:
12 000 - 2000 = 10 000 (đồng)
Hiện nay, với 60 000 đồng có thể mua được:
60 000 : 10 000 = 6 (m)
Đáp số: 6 m vải.
Câu 83:
Tìm 3 số, biết tổng số thứ nhất và số thứ hai là 182, tổng số thứ nhất và số thứ ba là 188, tổng số thứ hai và số thứ ba là 176.
 Xem đáp án
Xem đáp án
Tổng của ba số là:
(182 + 188 + 176) : 2 = 273
Số thứ nhất là:
273 - 176 = 97
Số thứ hai là:
273 - 188 = 85
Số thứ ba là:
273 - 182 = 91
Đáp số: Số thứ nhất: 97;
Số thứ hai: 85;
Số thứ ba: 91.
Câu 84:
Tìm số tự nhiên A khác 0, biết rằng:
a) A lớn nhất; 360 chia hết cho A và 560 chia hết cho A.
b) A khác 0; A nhỏ nhất; A chia hết cho 15 và chia hết cho 25.
 Xem đáp án
Xem đáp án
a) Ta có: 360 và 560 chia hết cho A Þ A Î ƯC(360, 560)
Mặt khác: A lớn nhất nên A = ƯCLN(360, 560)
Ta có: 360 = 23 . 32 . 5; 560 = 24 . 5 . 7.
Do đó A = ƯCLN(360, 560) = 23 . 5 = 40
Vậy A = 40.
b) Ta có: A chia hết cho 15 và 25 Þ A Î BC(15, 25)
Mặt khác A ≠ 0 và nhỏ nhất Þ A = BCNN(15, 25)
Ta có: 15 = 3 . 5; 25 = 52.
Do đó A = BCNN(15, 25) = 3 . 52 = 75.
Câu 85:
Tìm số tự nhiên có hai chữ số, biết rằng khi thêm chữ số 00 vào giữa hai chữ số của số đó ta được số mới gấp 6 lần số cũ.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là với a, b Î ℕ* và a, b £ 9; a ≠ 0
Theo bài ra ta có:
Þ 1000a + b = 6(10a + b)
Þ 940a = 5b
Þ 188a = b
Vì b £ 9 hay 188a £ 9 nên a < 1.
Mà a là số tự nhiên khác 0 nên vô lý
Vậy không tồn tại số thoả mãn
Câu 86:
Nếu chiều dài của một hình chữ nhật tăng lên gấp 3 lần, chiều rộng tăng lên gấp 2 lần thì diện tích hình chữ nhật đó tăng lên gấp mấy lần ?
 Xem đáp án
Xem đáp án
Nếu tăng chiều dài bao nhiêu lần thì diện tích tăng bấy nhiêu lần
Nếu tăng chiều rộng bao nhiêu lần thì diện tích tăng bấy nhiêu lần
Vậy diện tích tăng số lần là: 3 . 2 = 6 (lần)
Đáp số: 6 lần
Câu 87:
Trong hộp có ba loại bi là bi trắng, bi xanh và bi đỏ. Biết tổng số viên bi trong hộp nhiều hơn tổng số bi trắng và viên bi đỏ là 48 viên bi, số viên bi xanh nhiều hơn bi viên bi trắng 5 viên và ít hơn viên bi đỏ 12 viên. Tính tổng số viên bi trong hộp ?
 Xem đáp án
Xem đáp án
Ta có số bi xanh là 48 viên
Số bi trắng là:
48 - 5 = 43 (viên)
Số bi đỏ là:
48 + 12 = 60 (viên)
Tổng số viên bi trong hộp là:
48 + 43 + 60 = 151 (viên)
Đáp số: 151 viên
Câu 88:
 Xem đáp án
Xem đáp án
Ta có: M = 12 + 22 + 32 + ... + 992 + 1002
= 1 + 2(1 + 1) + ... + 99(98 + 1) + 100(99 + 1)
= 1 + 1.2 + 2 + ... + 98.99 + 99 + 99.100 + 100
= (1.2 + 2.3 + ... + 99.100) + (1 + 2 + ... + 99 + 100)
= 333 300 + 5050 = 338 050
Câu 89:
Cho 4 số tự nhiên không chia hết cho 5 khi chia hết cho 5 được những số dư khác nhau. Chứng minh rằng tổng của chúng chia hết cho 5
 Xem đáp án
Xem đáp án
Gọi 4 số đó là a + 1; a + 2; a + 3; a + 4
4 số đó chia cho 5 được những số dư khác nhau Þ Các số dư là 1; 2; 3 và 4
Giả sử (a + 1) : 5 dư 1; ....
Þ [(a + 1) - 1] = a ⋮ 5; ...
Tổng của chúng là:
(a + 1) + (a + 2) + (a + 3) + (a + 4) = a + 1 + a + 2 + a + 3 + a + 4
= 5a + 1 + 2 + 3 + 4 = 5a + 10
Vì 5a ⋮ 5 và 10 ⋮ 5
Þ Tổng của 4 số chia hết cho 5
Câu 90:
Cho xy + yz + zx = 0 và xyz ≠ 0. Tính giá trị biểu thức:
.
 Xem đáp án
Xem đáp án
Ta có: xy + yz + xz = 0
Chia cả 2 vế của đẳng thức trên cho xyz ≠ 0, ta được:
Nhận xét: Chú ý rằng nếu x + y + z = 0 (1) thì x3 + y3 + z3 = 3xyz (*)
Thật vậy, từ (1) Þ z = -(x + y)
Do đó, x3 + y3 + z3 = x3 + y3 - (x + y)3 = -3x2y - 3xy2 = -3xy(x + y) = 3xyz
Vậy, đẳng thức (*) được chứng minh
Áp dụng nhận xét trên, ta có:
Nếu thì
Do đó M =
(x, y, z ≠ 0)
Vậy .
Câu 91:
 Xem đáp án
Xem đáp án
Đặt A = 2.22 + 3.23 + 4.24 + ... + n.2n
Ta có: A = 2.22 + 3.23 + 4.24 + ... + n.2n
Suy ra 2A = 2(2.22 + 3.23 + 4.24 + ... + n.2n)
= 2.23 + 3.24 + 4.25 + ... + n.2n + 1
Do đó 2A - A = A = 2.22 + (3.23 - 2.23) + ... + (n - n + 1).2n - n.2n + 1
= 2.22 + 23 + 24 + ... + 2n -n.2n + 1
= 22 + (22 + 23 + 24 + ... + 2n + 1) - (n + 1) . 2n + 1
Đặt B = 22 + 23 + 24 + ... + 2n + 1
Suy ra 2B = 23 + 24 + 25 + ... + 2n + 2
Do đó 2B - B = B = 2n + 2 - 22
Þ B = 2n + 2 - 22 = 22 - 2n + 2 + 22 + (n + 1).2n + 1
= (n + 1).2n + 1 - 2n + 2
= 2n + 1(n + 1 - 2)
= (n - 1).2n+1 = 2(n - 1).2n
Mà A = 2(n - 1).2n = 2n + 11
Þ 2(n - 1) = 211 Þ n - 1 = 210
Þ n - 1 = 1024 Þ n = 1025
Vậy n = 1025.
Câu 92:
 Xem đáp án
Xem đáp án
Diện tích cây xanh bằng:
(diện tích công viên)
Đáp số: diện tích công viên.
Câu 93:
Giải phương trình : (0,4)x - (2,5)x+1 > 1,5
 Xem đáp án
Xem đáp án
(0,4)x - (2,5)x+1 > 1,5
Û
Đặt t = , BPT trở thành:
t -
Û t2 - 1,5t - > 0
Suy ra
Û x < -1
Vậy bất phương trình có tập nghiệm x < -1.
Câu 94:
Ba khối 6, 7 và 8 lần lượt có 300 học sinh, 276 học sinh và 252 học sinh xếp thành các hàng dọc để diễu hành sao cho số hàng dọc của mỗi khối là như nhau. Có thể xếp nhiều nhất thành mấy hàng dọc để mỗi khối đều không có ai lẻ hàng? Khi đó ở mỗi hàng dọc của mỗi khối có bao nhiêu học sinh?
 Xem đáp án
Xem đáp án
Do số hàng dọc của mỗi khối là như nhau nên số hàng dọc sẽ là ước chung của 300, 276, 252
Hơn nữa cần xếp nhiều nhất thành các hàng dọc để mỗi khối đều không có ai lẻ hàng nên số hàng là ƯCLN(300, 276, 252)
Ta có: 300 = 22 . 3 . 52
276 = 22 . 3 . 23
252 = 22 . 32 . 7
ƯCLN(300, 276, 252) = 22 . 3 = 12
Vậy có thể xếp nhiều nhất học sinh của ba khối 6, 7 và 8 thành 12 hàng.
Khi đó ở mỗi hàng:
+) Khối 6 có 300 : 12 = 25 (học sinh)
+) Khối 7 có 276 : 12 = 23 (học sinh)
+) Khối 8 có 252 : 12 = 21 (học sinh)
Câu 95:
Một sân trường hình chữ nhật có nửa chu vi là 120 m. Chiều rộng bằng chiều dài. Hỏi diện tích của sân trường đó bằng bao nhiêu mét vuông, bao nhiêu ha?
 Xem đáp án
Xem đáp án
Ta có sơ đồ:
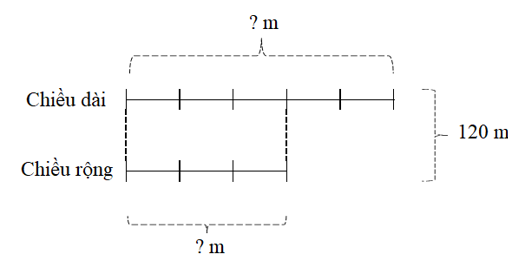
Theo sơ đồ, tổng số phần bằng nhau là:
3 + 5 = 8 (phần)
Chiều rộng sân trường đó là:
120 : (8 × 3) = 45 (m)
Chiều dài sân trường đó là:
120 - 45 = 75 (m)
Diện tích sân trường đó là:
75 × 45 = 3375 (m2)
Đổi 3 375 m2 = 0,3375 ha
Đáp số: 3 375 m2; 0,3375 ha.
