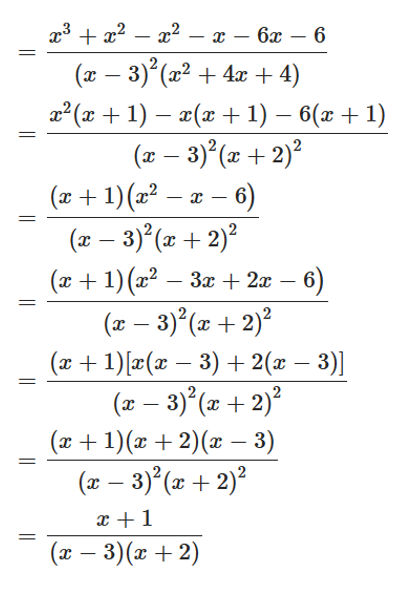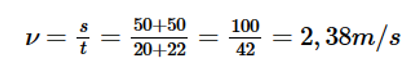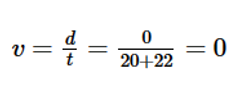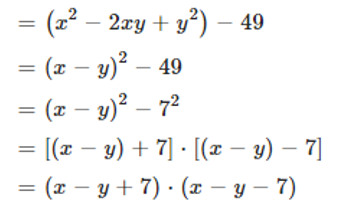Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 26)
-
2068 lượt thi
-
53 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Một cửa hàng có 7 gian chứa muối. Mỗi gian có 85 bao muối. Mỗi bao muối nặng 5 yến. Hỏi cửa hàng có tất cả bao nhiêu kg muối ? (giải bằng hai cách).
 Xem đáp án
Xem đáp án
Cách 1:
Số bao muối của 7 gian muối là:
85 × 7 = 595 (bao muối)
Khối lượng muối cửa hàng có tất cả là:
595 × 5 = 2 975 (yến muối)
Đổi 2 975 yến = 29 750 kg
Cách 2:
Số yến muối của mỗi gian muối là:
7 × 5 = 35 (yến)
Đổi 35 yến = 350 kg
Khối lượng muối của hàng tất cả là:
350 × 85 = 29 750 (kg muối)
Vậy cửa hàng có 29 750 kg muối.
Câu 2:
Một người đổ thêm 50 gam muối vào một bình chứa 350 gam nước muối loại 10 % muối. Hỏi người đó nhận được một bình nước chứa bao nhiêu phần trăm muối?
 Xem đáp án
Xem đáp án
Khối lượng muối trong 350 g nước muối loại 10% là:
350 : 100 × 10 = 35 (g)
Khối lượng muối sau khi thêm vào là :
50 + 35 = 85 (g)
Tỉ lệ phần trăm muối cần tìm là :
85 × 100 : (350 + 50) = 21,25%
Vậy khi đó bình nước chứa 21, 25% muối.
Câu 4:
Tìm n thuộc ℕ để thuộc ℕ.
 Xem đáp án
Xem đáp án
Ta có:
Để thì
⇔ 9 ⋮ n – 2
⇔ n – 2 ∈ Ư(9) = {1; 3; 9; –1; –3; –9}
⇔ n ∈ {3; 5; 11; 1; –1; –7}
Mà n ∈ ℕ
Suy ra n ∈ {3; 5; 11; 1}
Vậy n ∈ {3; 5; 11; 1}.
Câu 5:
Trong một cuộc thi chạy 100m, bạn Trung chạy hết phút, bạn Minh chạy hết phút. Bạn nào chạy nhanh hơn và nhanh hơn bao nhiêu giây?
 Xem đáp án
Xem đáp án
Đổi 1 phút = 60 giây
Bạn Trung chạy hết số giây là:
(giây)
Bạn Minh chạy hết số giây là:
(giây)
Bạn Trung chạy nhanh hơn và nhanh hơn số giây là:
20 – 15 = 5 (giây)
Vậy Trung chạy nhanh hơn Minh và nhanh hơn 5 giây.
Câu 6:
Có một tuần trung bình nhà máy A mỗi ngày tiêu thụ hết 1 165 250 lít nước, nhà máy B mỗi ngày tiêu thụ hết 8 071 750 lít nước. Hỏi trong cả tuấn đó, hai nhà máy tiêu thụ bao nhiêu lít nước?
 Xem đáp án
Xem đáp án
Trong 1 tuần nhà máy A tiêu thụ hết:
1 165 250 × 7 = 8 156 750 (lít nước)
Trong 1 tuần nhà máy B tiêu thụ hết:
8 071 750 × 7 = 56 502 250 (lít nước)
Trong cả tuần đó, hai nhà máy tiêu thụ hết:
8 156 750 + 56 502 250 = 64 659 000 (lít nước)
Vậy trong cả tuần đó, hai nhà máy tiêu thụ hết 64 659 000 lít nướcCâu 7:
Tính:
a) (10 – 9,34) + (10 – 9,66);
b) 12 – (12 – 9,36).
 Xem đáp án
Xem đáp án
a) (10 – 9,34) + (10 – 9,66)
= 10 – 9,34 + 10 – 9,66
= (10 + 10) + (–9,34 – 9,66)
= 20 – 19
= 1.
b) 12 – (12 – 9,36)
= 12 – 12 + 9,36
= 0 + 9,36
= 9,36.
Câu 8:
Tìm số nguyên x, y thỏa mãn (x + 3)2022 + (y – 2)2022 = 0.
 Xem đáp án
Xem đáp án
Vì (x + 3)2022 ≥ 0 với mọi x
(y – 2)2022 ≥ 0 với mọi y
Nên (x + 3)2022 + (y – 2)2022 ≥ 0 với mọi x, y
Dấu “ = ” xảy ra khi
Vậy x = –3, y = 2 là nghiệm của phương trình đã cho.
Câu 9:
 Xem đáp án
Xem đáp án
Vì x là tổng các số nguyên có 2 chữ số
Nên x = 0
Vì y số nguyên âm lớn nhất
Nên y = –1
Thay x = 0, y = –1 vào A ta có:
A = 2009 . 02006 – 2008 . (–1)2007
A = 2009 . 0 – 2008 . (–1)
A = 0 + 2008
A = 2008.
Câu 10:
Cho tam giác ABC vuông tại C, đường cao CH, lấy điểm M trên AB và điểm N trên AC sao cho BM = BC và CN = CH. Chứng minh MN vuông góc với AC.
 Xem đáp án
Xem đáp án
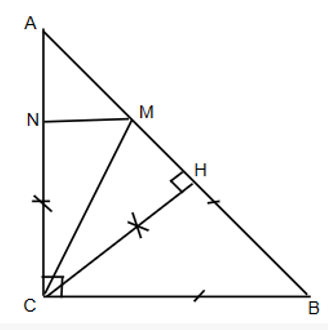
Xét tam giác MCB có: BM = BC (giả thiết)
Suy ra tam giác MCB cân tại B, nên
Xét tam giác CHM vuông tại H có (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Hay
Ta có:
Hay
Mà , suy ra
Xét tam giác MCH và tam giác MCN có:
CH = CN (giả thiết);
(chứng minh trên);
CM chung
Do đó ∆MCH = ∆MCN (c.g.c)
Suy ra
Mà , do đó
Hay MN vuông góc với AC
Vậy MN vuông góc với AC.
Câu 11:
 Xem đáp án
Xem đáp án
Ta thấy
98 quay ngược được 86
88 quay ngược được 88
68 quay ngược được 898
06 quay ngược được 90
16 quay ngược được 91
Suy ra số nằm giữa 86 và 88 là 87
Vậy số cần tìm là 87.
Câu 12:
Hai đội công nhân cùng đào một con đường dài 900 m, đội thứ nhất đào ít hơn đội thứ hai 164 m. Hỏi mỗi đội đào được bao nhiêu mét đường?
 Xem đáp án
Xem đáp án
Ta thấy nếu đội thứ hai bớt đi 164 m thì bằng đội thứ nhất, vậy tổng trừ đi hiệu thì được 2 lần đội thứ nhất.
Đội thứ nhất đào được số mét đường là:
(900 – 164) : 2 = 368 (m)
Đội thứ hai đào được số mét đường là:
900 – 368 = 532 (m)
Vậy đội thứ nhất đào được 368 m, đội thứ hai đào được 532 m.
Câu 13:
Tính hợp lý: (102 + 112 + 122) : (132 + 142).
 Xem đáp án
Xem đáp án
Ta có:
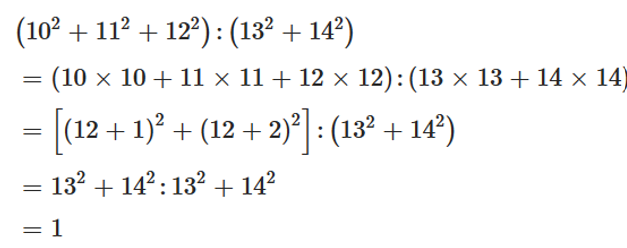
Vậy (102 + 112 + 122) : (132 + 142) = 1.
Câu 15:
 Xem đáp án
Xem đáp án
Ta có a + b + c + d = 0
⇔ a + b = – c – d
⇔ (a + b)3 = (– c – d)3
⇔ a3 + b3 + 3ab(a + b) = – c3 – d3 – 3cd(c + d)
⇔ a3 + b3 + c3 + d3 = – 3cd(c + d) – 3ab(a + b)
⇔ a3 + b3 + c3 + d3 = – 3cd(c + d) + 3ab(c + d)
⇔ a3 + b3 + c3 + d3 = 3(c + d)(ab – cd)
Vậy a3 + b3 + c3 + d3 = 3(c + d)(ab – cd).
Câu 16:
Cho hình thang ABCD (AB // CD) và AB = BC.
a) Chứng minh CA là phân giác của góc BCD.
 Xem đáp án
Xem đáp án
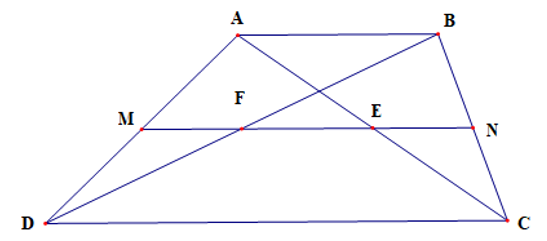
a) Vì AB = BC (giả thiết) nên tam giác ABC cân tại B
Suy ra
Vì AB // CD nên
Do đó
Suy ra CA là tia phân giác của .
Câu 17:
b) Gọi M, N, E, F lần lượt là trung điểm của AD, BC, AC, BD. Chứng minh M, N, E, F thẳng hàng.
 Xem đáp án
Xem đáp án
b) Xét ΔABD có: F, M lần lượt là trung điểm của BD, AD
Suy ra MF là đường trung bình của ΔABD
Do đó MF // AB
Xét ΔACD có: M, E lần lượt là trung điểm của AD, AC
Suy ra ME là đường trung bình của ΔABC
Do đó ME // CD
Xét ΔABC có: N, E lần lượt là trung điểm của BC, AC
Suy ra NE là đường trung bình của ΔABC
Do đó NE // AB
Xét ΔBCD có: F, N lần lượt là trung điểm của BD, BC
Suy ra NF là đường trung bình của ΔABC
Do đó NF // CD
Ta có:
AB // CD, NF // CD, NE // AB, MF // AB, ME // CD
Suy ra N, E, F, M thẳng hàng
Vậy N, E, F, M thẳng hàng.
Câu 18:
Cho tứ giác ABCD (AB không song song với CD). Giả sử M, N lần lượt là trung điểm của AB và CD, thỏa mãn: . Chứng minh: ABCD là hình thang.
 Xem đáp án
Xem đáp án
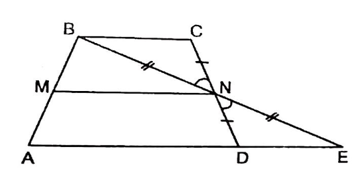
Trên tia BN lấy điểm E sao cho N là trung điểm của BE
Xét tam giác NBC và tam giác NED có:
BN = EN;
(hai góc đối đỉnh);
CN = ND (giả thiết)
Suy ra ∆NBC = ∆NED (c.g.c)
Do đó DE = BC (hai cạnh tương ứng) và (hai góc tương ứng)
Mà hai góc và ở vị trí so le trong, suy ra BC // DE
Ta có:
Xét tam giác ABE có M, N là trung điểm của AB, BE
Suy ra MN là đường trung bình của tam giác ABE
Do đó MN // AE và
Mà
Suy ra DE + AD = AE
Do đó A, D, E thẳng hàng
Mà BC // DE, suy ra BD // AD
Hay ABCD là hình thang
Vậy ABCD là hình thang.
Câu 19:
Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Sắp xếp cụm số 3, 4, 5 có 2 cách sắp xếp là 345 và 543
TH1: Cụm 2 số 3, 4, 5 đứng đầu có:
2 . 7 . 6 . 5 = 240 số thỏa mãn
TH2: Cụm 3 số 3, 4, 5 không đứng đầu có 3 cách sắp xếp là
3 chữ số còn lại có: 6 . 6 . 5 = 180 cách chọn và sắp xếp
Do đó có 2 . 3 . 180 = 1 080 số thỏa mãn
Theo quy tắc cộng có:
420 + 1 080 = 1 500 số thỏa mãn yêu cầu bài toán
Vậy ta chọn đáp án D.
Câu 20:
Hai thùng chứa 100 lít dầu. Sau khi đổ 10 lít từ thùng 1 sang thùng thứ 2 thì số dầu thùng thứ 2 bằng số ở thùng 1. Hỏi ban đầu mỗi thùng có bao nhiêu lít dầu?
 Xem đáp án
Xem đáp án
Sau khi đổ 10 lít từ thùng 1 sang thùng 2 thì tổng số lít dầu không thay đổi (vẫn là 100 lít)
Số lít dầu của thùng 1 sau khi chuyển là:
100 : (2 + 3) × 3 = 60 (l)
Số lít dầu của thùng 2 sau khi chuyển là:
100 : (2 + 3) × 2 = 40 (l)
Số lít dầu của thùng 1 ban đầu là:
60 + 10 = 70 (l)
Số lít dầu của thùng 2 ban đầu là:
40 – 10 = 30 (l)
Vậy ban đầu thùng 1 có 70 lít dầu và thùng 2 có 30 lít dầu.
Câu 21:
Tổng của các số tự nhiên liên tiếp từ 1 đến n là 1 số có 3 chữ số giống nhau. Tìm số tự nhiên n.
 Xem đáp án
Xem đáp án
Gọi số có 3 chữ số giống nhau là
Ta có:
⇔ n(n + 1) = 2 . 111 . a
⇔ n(n + 1) = 222 . a
⇔ n(n + 1) = 6 . 37 . a
Vì 6 . 37 . a chia hết cho 37
Nên n(n + 1) cũng chia hết cho 37
Suy ra n hoặc (n + 1) phải chia hết cho 37
Mà 6 . a ≤ 6 . 9
Hay 6 . a ≤ 54
Ta có 36 . 37 hoặc 37 . 38
Vì 38 không chia hết cho 6 nên n = 36 và n + 1 = 37
Vậy n = 36.
Câu 22:
Cho hình thang cân ABCD có đáy lớn AB = 30 cm, đáy nhỏ CD = 10 cm và .
a) Tính cạnh BC.
 Xem đáp án
Xem đáp án

a) Kẻ CH ⊥ AB, DK ⊥ AB
Suy ra DK // CH (quan hệ từ vuông góc đến song song)
Mà CD // HK
Suy ra CDKH là hình bình hành
Lại có nên CDKH là hình chữ nhật
Suy ra KH = CD = 10 (cm)
Vì ABCD là hình thang cân nên AD = BC và
Xét ∆AKD và ∆BHC có
(chứng minh trên);
AD = BC (chứng minh trên);
Do đó ∆AKD = ∆BHC (cạnh huyền – góc nhọn)
Suy ra AK = BH
Ta có AB = AK + KH + BH = 30
Hay 2AK + 10 = 30
Suy ra AK = BH = 10 (cm)
Xét tam giác BCH vuông ở H
Suy ra (cm)
Câu 23:
 Xem đáp án
Xem đáp án
b) Xét tam giác BCH vuông ở H
Suy ra (cm)
Ta có
Vì N là trung điểm của CD nên
Suy ra MH = NC
Mà MH // NC
Suy ra MHCN là hình bình hành, nên MN = HC
Mà , suy ra
Vậy
Câu 24:
Tìm số tự nhiên có bốn chữ số, biết rằng khi viết thêm chữ số 7 vào bên phải số đó thì được số có năm chữ số lớn hơn số phải tìm 11 212 đơn vị.
 Xem đáp án
Xem đáp án
Gọi số tự nhiên có 4 chữ số cần tìm là
Sau khi viết thêm chữ số 7 vào bên phải số đó thì được số mới là
Ta có:
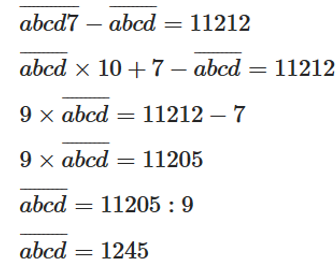
Vậy số cần tìm là 1245.
Câu 27:
Tìm số hữu tỉ a sao cho x3 + ax2 + 5x + 3 chia hết cho x2 + 2x + 3.
 Xem đáp án
Xem đáp án
Đặt f(x) = x3 + ax2 + 5x + 3 và g(x) = x2 + 2x + 3
h(x) là thương của phép chia f(x) cho g(x)
Ta có f(x) bậc 3, g(x) bậc 2 nên h(x) bậc 1
Suy ra h(x) có dạng x + b
Vì f(x) ⋮ g(x) nên f(x) = g(x) . h(x)
⇔ x3 + ax2 + 5x + 3 = (x2 + 2x + 3)(x + b)
⇔ x3 + ax2 + 5x + 3 = x3 + bx2 + 2x2 + 2xb + 3x + 3b
⇔ x3 + ax2 + 5x + 3 = x3 + x2(b + 2) + x(2b + 3) + 3b
Vậy a = 3.
Câu 28:
Một phân xưởng có 24 máy dệt, mỗi ngày dệt được 264 áo. Nếu phân xưởng đó có thêm 12 máy nữa thì mỗi ngày dệt được tất cả bao nhiêu áo? (Năng suất mỗi máy không đổi).
 Xem đáp án
Xem đáp án
Nếu thêm 12 máy nữa thì phân xưởng có:
24 + 12 = 36 (máy)
Mỗi máy dệt được số áo mỗi ngày là:
264 : 24 = 11 (cái áo)
Mỗi ngày 36 máy dệt được là:
36 × 11 = 396 (cái áo)
Vậy thêm 12 máy nữa thì mỗi ngày dệt được 396 cái áo.
Câu 29:
 Xem đáp án
Xem đáp án
Ta có:
12x2 + 6xy + 3y2 = 28(x + y)
⇔ 12x2 + 6xy + 3y2 – 28(x + y) = 0
⇔ 3y2 + 2y(3x – 14) + 12x2 – 28x = 0 (1)
Xem (1) là phương trình bậc 2 ẩn y
Thì (1) có nghiệm nguyên khi và chỉ khi ∆’ là số chính phương
∆’ = (3x – 14)2 – 3(12x2 – 28x) = 9x2 – 84x + 196 – 36x2 + 84x
= 196 – 27x2 = k2 ≥ 0
Suy ra 27x2 ≤ 196 hay x2 ≤ 7,26
Do đó x ∈ {0; 1; 2; –1; –2}
+) Thay x = 0 vào (1) ta có
3y2 + 2y(3 . 0 – 14) + 12 . 02 – 28 . 0 = 0
⇔ 3y2 – 28y = 0
⇔ y(3y – 28) = 0
(vì y ∈ ℤ)
+) Thay x = 1 vào (1) ta có
3y2 + 2y(3 . 1 – 14) + 12 . 12 – 28 . 1 = 0
⇔ 3y2 – 22y – 16 = 0
⇔ (y – 8)(2y + 3) = 0
(vì y ∈ ℤ)
+) Thay x = –1 vào (1) ta có
3y2 + 2y[3 . (–1) – 14] + 12 . (–1)2 – 28 . (–1) = 0
⇔ 3y2 – 34y + 40 = 0
⇔ (y – 10)(3y + 4) = 0
(vì y ∈ ℤ)
+) Thay x = 2 vào (1) ta có
3y2 + 2y(3 . 2 – 14) + 12 . 22 – 28 . 2 = 0
⇔ 3y2 – 8y – 8 = 0 (không có nghiệm y nguyên)
+) Thay x = –2 vào (1) ta có
3y2 + 2y[3 . (–2) – 14] + 12 . (–2)2 – 28 . (–2) = 0
⇔ 3y2 – 20y + 80 = 0 (vô nghiệm)
Vậy phương trình có nghiệm x, y nguyên là (0; 0), (1; 8), (–1; 10).
Câu 30:
Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ (M thuộc OP), IN // OP (N thuộc OQ). Chứng minh rằng:
a) Tam giác IMN cân tại I.
 Xem đáp án
Xem đáp án
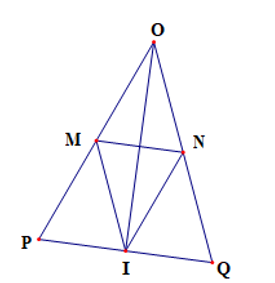
a) Xét ΔOPQ có: I là trung điểm của PQ và IN // OP
Do đó N là trung điểm của OQ
Xét ΔOPQ có: I là trung điểm của PQ và IM // OQ
Do đó M là trung điểm của OP
Vì tam giác OPQ cân tại O nên và OP = OQ
Suy ra MP = NQ = OM = ON
Xét ΔMPI và ΔNQI có
MP = NQ (chứng minh trên);
(chứng minh trên);
PI = QI (giả thiết)
Do đó: ΔMPI = ΔNQI (c.g.c)
Suy ra: IM = IN (hai cạnh tương ứng)
Hay ΔIMN cân tại I.
Câu 31:
b) OI là đường trung trực của MN.
 Xem đáp án
Xem đáp án
b) Ta có: OM = ON (chứng minh câu a)
Nên O nằm trên đường trung trực của MN (1)
Ta có: IM = IN (chứng minh câu a)
Nên I nằm trên đường trung trực của MN (2)
Từ (1) và (2) suy ra OI là đường trung trực của MN
Vậy OI là đường trung trực của MN.
Câu 32:
Một người bơi dọc trong bể bơi dài 50 m. Bơi từ đầu bể đến cuối bể hết 20 giây, bơi tiếp từ cuối bể quay về đầu bể hết 22 giây. Xác định tốc độ trung bình và vận tốc trung bình trong 3 trường hợp sau:
a) Bơi từ đầu bể đến cuối bể.
 Xem đáp án
Xem đáp án
a) Bơi từ đầu bể đến cuối bể, trong quá trình này người chuyển động thẳng, không đổi chiều chuyển động nên quãng đường và độ dịch chuyển bằng nhau và bằng chiều dài của bể: s = d = 50 m
Tốc độ trung bình bằng vận tốc trung bình:
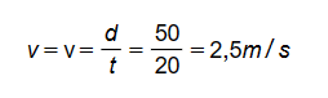
Câu 33:
b) Bơi từ cuối bể về đầu bể.
 Xem đáp án
Xem đáp án
b) Bơi từ cuối bể về đầu bể
Tốc độ trung bình:
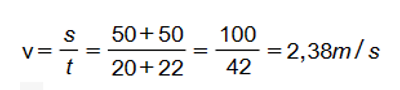
Vận tốc trung bình:
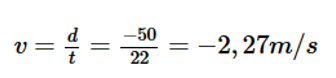
Câu 36:
Viết kết quả viết dưới dạng lũy thừa:
a) 125 : 52;
b) 275 : 813;
 Xem đáp án
Xem đáp án
a) 125 : 52 = 53 : 52 = 53-2 = 5.
b) 275 : 813 = (33)5 : (34)3 = 315 : 312 = 315-12 = 33.
Câu 37:
Viết kết quả viết dưới dạng lũy thừa:
c) 84 × 165 × 32;
d) 274 × 8110 .
 Xem đáp án
Xem đáp án
c) 84 × 165 × 32 = (23)4 × (24)5 × 25 = 212 × 220 × 25 = 212+20+5 = 237.
d) 274 × 8110 = (33)4 × (34)10 = 312 × 340 = 312+40 = 352.
Câu 38:
Tính nhanh:
a) 342 + 662 + 68 . 66;
b) 742 + 242 – 48 . 74.
 Xem đáp án
Xem đáp án
a) 342 + 662 + 68 . 66
= 342 + 2 . 34 . 66 + 662
= (34 + 66)2
= 1002
= 10 000.
b) 742 + 242 – 48 . 74
= 742 – 2 . 74 . 24 + 242
= (74 – 24)2
= 502
= 2 500.
Câu 39:
Cho số tự nhiên có 3 chữ số, biết rằng nếu thêm một chữ số 0 vào giữa chữ số hàng trăm và hàng chục của số đó ta được một số gấp 6 lần số đã cho.
 Xem đáp án
Xem đáp án
Gọi số phải tìm là
Ta có:
Để có 2 chữ số thì a < 2
Suy ra a = 1
Do đó
Vậy số phải tìm là 180.
Câu 40:
Cho tam giác ABC (AB < AC) đường cao AH. Gọi M, N, P lần lượt là trung điểm của cạnh BC, CA, AB.
a) Chứng minh NP là đường trung trực của AH.
 Xem đáp án
Xem đáp án
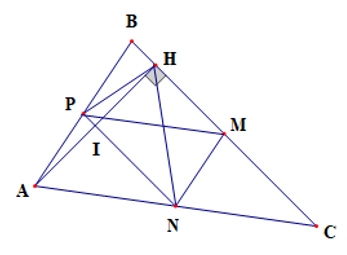
a) Gọi I là giao điểm của AH và PN
Xét tam giác ABC có P, N là trung điểm của AB, AC
Do đó PN là đường trung bình của tam giác ABC
Suy ra PN // BC
Mà AH ⊥ BC nên PN ⊥ AH (1)
Ta có : PN // BC mà PI thuộc PN nên PI // BC
Xét tam giác AHB có PI // BC và P là trung điểm của AB
Suy ra I là trung điểm của AH (2)
Từ (1) và (2) suy ra PN là đg trung trực của AH.
Câu 41:
b) Chứng minh tứ giác MNPH là hình thang cân.
 Xem đáp án
Xem đáp án
b) Xét tứ giác MNPH có HM // PN
Suy ra tứ giác MNPH là hình thang
Xét tam giác ABC có P, M là trung điểm của AB, BC
Suy ra PM là đường trung bình của tam giác ABC
Do đó
Xét tam giác AHC vuông tại H có HN là đường trung tuyến ứng với cạnh huyền AC
Suy ra
Mà , do đó HN = PM
Xét hình thang MNPH có PM = HN
Suy ra MNPH là hình thang cân (dấu hiệu)
Vậy MNPH là hình thang cân.
Câu 42:
Cho tam giác ABC nhọn. Gọi M và N lần lượt là trung điểm của AB, BC
a) Tính độ dài của MN biết AC = 16 cm.
b) Gọi I là trung điểm của AC. Chứng minh tứ giác BMIN là hình bình hành.
 Xem đáp án
Xem đáp án
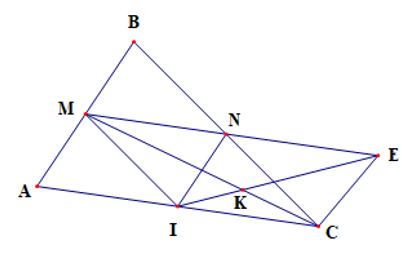
a) Xét ΔABC có M, N là trung điểm của AB, BC
Do đó MN là đường trung bình của ΔBAC
Suy ra: MN // AC và (cm)
Câu 43:
b) Gọi I là trung điểm của AC. Chứng minh tứ giác BMIN là hình bình hành.
 Xem đáp án
Xem đáp án
b) Xét ΔBAC có M, I là trung điểm của AB, AC
Do đó: MI là đường trung bình của ΔBAC
Suy ra: MI // BC và
Mà
Nên MI // BN và MI = BN
Suy ra BMIN là hình bình hành.
Câu 44:
c) Trên tia đối của tia NM lấy E sao cho N là trung điểm ME. Gọi K là giao điểm của EI và MC. Chứng minh MC = 3KC.
 Xem đáp án
Xem đáp án
c) Ta có và MN = NE
Suy ra ,
Mà EN // IC
Do đó NECI là hình bình hành
Mà MC cắt IE tại K
Suy ra
Hay
Do đó KM = 2KC
Ta có MC = KC + KM = KC + 2KC = 3KC
Vậy MC = 3KC.
Câu 45:
Cho tam giác ABC vuông tại A, đường cao AH, M là trung điểm của BC, có BH = 4 cm, CH = 9 cm. Tính diện tích tam giác AHM.
 Xem đáp án
Xem đáp án
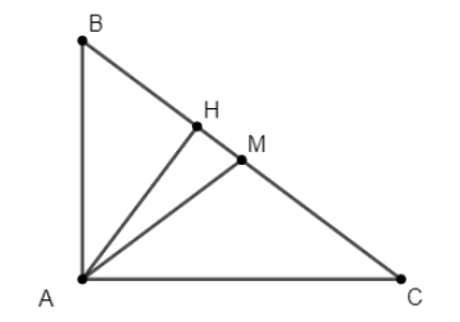
Vì ABC vuông tại A và AH là đường cao nên ta có:
AH2 = BH . HC = 4 . 9 = 36
Suy ra AH = 6 (cm)
Vì AM là đường trung tuyến của ∆ABC nên ta có:
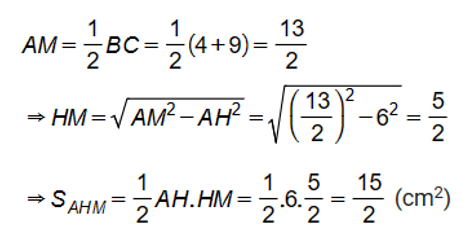
Vậy diện tích tam giác AHM là cm2.
Câu 46:
Một cửa hàng có 30 kg gạo, ngày thứ nhất cửa hàng bán số gạo, ngày thứ hai cửa hàng bán số gạo còn lại. Hỏi ngày thứ hai cửa hàng bán bao nhiêu kg gạo?
 Xem đáp án
Xem đáp án
Ngày thứ nhất cửa hàng bán được số gạo là
(kg)
Sau khi bán buổi sáng cửa hàng cón lại số gạo là
30 – 6 = 24 (kg)
Ngày thứ hai cửa hàng bán được số gạo là
(kg)
Vậy ngày thứ hai cửa hàng bán được 6 kg gạo.
Câu 47:
Cửa hàng bán số gạo tẻ nhiều hơn số gạo nếp 36 kg, trong đó số gạo nếp bằng số gạo tẻ. Hỏi mỗi loại bán được bao nhiêu kg?
 Xem đáp án
Xem đáp án
Số kg gạo nếp bán được là:
36 : (5 – 3) × 3 = 54 (kg)
Số kg gạo tẻ bán được là:
54 + 36 = 90 (kg)
Vậy cửa hàng bán được 54 kg gạo nếp và 90 kg gạo tẻ.
Câu 48:
Hai bác thợ cưa một cây gỗ dài 7 m thành những đoạn dài 1 m. Cứ 12 phút thì cưa xong một đoạn. Hỏi cưa cả cây gỗ đó hết bao lâu?
 Xem đáp án
Xem đáp án
Cưa cây gỗ dài 7 m được số đoạn là:
7 : 1 = 7 (đoạn)
Cưa cả cây gỗ đó hết:
7 × 12 = 84 (phút)
Vậy cưa cả cây gỗ hết 84 phút.
Câu 49:
May 3 bộ quần áo hết 7 m vải. Hỏi may 9 bộ quần áo như thế hết bao nhiêu mét vải?
 Xem đáp án
Xem đáp án
9 bộ gấp 3 bộ số lần là:
9 : 3 = 3 (lần)
May 9 bộ quần áo cần số mét vải là:
7 × 3 = 21 (m)
Vậy may 9 bộ quần áo hết 21 m vải.
Câu 50:
 Xem đáp án
Xem đáp án
Số người công nhân hiện có là:
9 + 18 = 27 (người)
27 người đắp được số m đường là:
27 : 9 × 60 = 180 (m)
Vậy bổ sung thêm 18 người nữa cùng đắp thì trong một ngày đắp được 180 mét đường.
Câu 51:
Mẹ có 1 số tiền nếu mua táo với giá 8 000 đồng 1 kg thì mẹ mua được 3 kg. Hỏi nếu mua mận với giá 6 000 một kg thì mẹ mua được bao nhiêu kg mận ?
 Xem đáp án
Xem đáp án
Số tiền mẹ có là: 8 000 × 3 = 24 000 (đồng)
Số ki – lô – gam mận mẹ mua được là:
24 000 : 6 000 = 4 (kg)
Vậy mẹ mua được 4 kg mận.
Câu 52:
Một bếp ăn tập thể dự trữ gạo đủ cho 85 người ăn trong 18 ngày. Sau đó vì có thêm người đến ăn nên số gạo chỉ đủ ăn trong 15 ngày. Hỏi có bao nhiêu người đến ăn thêm (mức ăn mỗi người bằng nhau).
 Xem đáp án
Xem đáp án
1 ngày có số người ăn hết từng đó số gạo là:
85 × 18 = 1 530 (người)
Trong 15 ngày thì có số người ăn hết là:
1 530 : 15 = 102 (người)
Số người đến ăn thêm là:
102 – 85 = 17 (người)
Vậy có 17 người đến ăn thêm.
Câu 53:
Một máy in cần 5 giây để in 1 trang giấy và cứ sau 1 giờ in liên tục thì cần 4 phút để máy in nghỉ. Hỏi mất bao nhiêu phút để máy in sẽ in hết 3 600 trang giấy.
 Xem đáp án
Xem đáp án
Số giây để in hết 3 600 trang giấy là:
3 600 × 5 = 18 000 (giây)
Đổi 18 000 giây = 300 phút = 5 giờ
Số phút để máy nghỉ là:
4 × 5 = 20 (phút)
Thời gian để in hết 3 600 trang giấy là:
300 + 20 = 320 (phút)
Vậy cần 320 phút để in hêt 3 600 trang giấy.