80 câu trắc nghiệm Khối đa diện nâng cao phần 2 (có đáp án)
-
1890 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hình lăng trụ ABC. A'B'C' có đáy ABC là tam giác vuông tại A; AB=1; AC=2. Hình chiếu vuông góc của A' trên (ABC) nằm trên đường thẳng BC. Tính khoảng cách từ điểm A đến mặt phẳng (A'BC).
 Xem đáp án
Xem đáp án
Chọn C
Gọi H là hình chiếu vuông góc của A' lên (ABC).
Từ A kẻ AK BC
Xét vuông tại A, có :
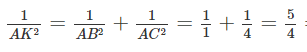
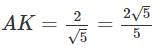
Vậy
Câu 2:
Cho khối lăng trụ ABC. A'B'C' có thể tích bằng 2018. Gọi M là trung điểm AA' ; N, P lần lượt là các điểm nằm trên các cạnh BB', CC' sao cho BN=2B'N, CP=3C'P. Tính thể tích khối đa diện ABC. MNP.
 Xem đáp án
Xem đáp án
Chọn D
Câu 3:
Cho khối tứ diện ABCD có thể tích 2017. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính thể tích của khối tứ diện MNPQ.
 Xem đáp án
Xem đáp án
Chọn D
(Do E, F, G lần lượt là trung điểm của BC, BD, CD).
Do mặt phẳng (MNP) // (BCD) nên
Câu 4:
Cho hình lăng trụ ABC. A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng . Tính theo a thể tích V của khối lăng trụ ABC. A'B'C'.
 Xem đáp án
Xem đáp án
Chọn B
Gọi G là trọng tâm tam giác ABC và M là trung điểm của BC
Ta có nên
Kẻ ; nên
Kẻ , ta có
Câu 5:
Cho hình lăng trụ đứng ABC. A'B'C', biết đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng .Tính thể tích khối lăng trụ ABC. A'B'C'.
 Xem đáp án
Xem đáp án
Chọn D
Diện tích đáy là
Chiều cao là h = d((ABC); (A'B'C')) = AA'
Do tam giác ABC là tam giác đều nên O là trọng tâm của tam giác ABC. Gọi I là trung điểm của BC, H là hình chiếu vuông góc của A lên A'I ta có:
Xét tam giác A'AI vuông tại A ta có:
Câu 6:
Cho khối tứ diện ABCD có thể tích bằng V, thể tích của khối đa diện có đỉnh là trung điểm các cạnh của tứ diện ABCD bằng V'. Tính tỉ số V'/V.
 Xem đáp án
Xem đáp án
Chọn A
Câu 7:
Cho khối chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và (ABCD) bằng . Gọi M, N lần lượt là trung điểm AB, AD. Tính thể tích khối chóp S. CDMN theo a.
 Xem đáp án
Xem đáp án
Chọn C
nên góc giữa mặt phẳng (SBC) và (ABCD) là . Do đó
SA = AB tan450 = a
Diện tích là:
![]()
Diện tích là:
![]()
Ta có:
Vậy:
Câu 8:
Cho hình chóp tam giác S. ABC có đáy ABC là tam giác đều cạnh a, SA=a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A. BCNM bằng:
 Xem đáp án
Xem đáp án
Chọn D
Thể tích khối chóp S. ABC là:
Do SA = AB = AC = a nên các tam giác SAC, SAB cân tại A.
Theo đề bài M, N là hình chiếu của A trên SB, SC nên M, N lần lượt là trung điểm SB, SC.
Khi đó:
Vậy thể tích khối chóp A. BCNM là:
Câu 9:
Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng . Gọi M, N lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN là:
 Xem đáp án
Xem đáp án
Chọn C
Gọi O là tâm của hình vuông ABCD. Kẻ ON vuông góc với DC
Góc giữa mặt bên (SAB) và mặt đáy là góc
Xét tam giác SNO, ta có
Lại có M là trung điểm của SD nên:
N là trung điểm của CD nên
![]()
Do đó, thể tích khối MACN là
Câu 10:
Cho tứ diện ABCD có AB = AD = , B.C = BD = a và CA = CD = x. Khoảng cách từ B đến mặt phẳng (ACD) bằng . Biết thể tích của khối tứ diện bằng Góc giữa hai mặt phẳng (ACD) và (BCD) là:
 Xem đáp án
Xem đáp án
Chọn C
Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
Tam giác ACD có CA=CD=x=a ; AD = tam giác ACD vuông cân tại AC
Mặt khác:
Tam giác ABD có:
Tam giác BHK có:
=> Tam giác BHK vuông tại H
![]()
Câu 11:
Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 2a. Mặt bên của hình chóp tạo với mặt đáy một góc 600. Mặt phẳng (P) chứa AB và đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M và N. Thể tích khối chóp S. ABMN là:
 Xem đáp án
Xem đáp án
Chọn A
Gọi H là trung điểm cạnh CD và O là tâm hình vuông ABCD.
Ta có S. ABCD là hình chóp tứ giác đều nên các mặt bên hợp với đáy các góc bằng nhau
Giả sử
![]()
Tam giác SHO vuông tại O có:
Mà G là trọng tâm tam giác SAC nên G cũng là trọng tâm tam giác SBD
Câu 12:
Cho hình chóp tứ giác S. ABCD đáy là hình bình hành có thể tích bằng V. Lấy điểm B', D' lần lượt là trung điểm của cạnh SB và SD. Mặt phẳng qua (AB'D') cắt cạnh SC tại C'. Khi đó thể tích khối chóp S. AB'C'D' bằng:
 Xem đáp án
Xem đáp án
Chọn D
Gọi O là giao điểm của hai đường chéo AC và BD thì SO ∩ DD' = H. Khi đó H là trung điểm của SO và C' = AH ∩ SC.
Trong mặt phẳng (SAC) : Ta kẻ d // AC và AC' cắt (d) tại K. Khi đó áp dụng tính đồng dạng của các tam giác ta có:
Suy ra:
Lưu ý: Có thể sử dụng nhanh công thức:
Câu 13:
Cắt khối hộp ABCD. A'B'C'D' bởi các mặt phẳng (AB'D'), (CB'D'), (B'AC), (D'AC) ta được khối đa diện có thể tích lớn nhất là:
 Xem đáp án
Xem đáp án
Chọn C
Khi cắt khối hộp bởi các mặt phẳng trên ta được 5 khối tứ diện AA'B'D', B'ABC, CC'B'D', D'DAC, AB'D'C. Gọi V là thể tích của khối hộp.
Suy ra nên tứ diện ACB'D' có thể tích lớn nhất.
Câu 14:
Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết . Tính thể tích V của khối chóp S. ABC.
 Xem đáp án
Xem đáp án
Chọn B
Ta có . Gọi H là hình chiếu vuông góc của A trên SM. Do
và FE đi qua H.
Vậy H là trung điểm cạnh SM. Suy ra tam giác SAM vuông cân tại A
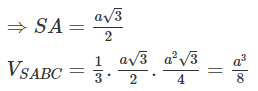
Câu 15:
Cho lăng trụ tam giác đều ABC. A'B'C' có cạnh đáy bằng a và . Tính thể tích V của khối lăng trụ đã cho.
 Xem đáp án
Xem đáp án
Chọn C
Gọi E là điểm đối xứng của C qua điểm B. Khi đó tam giác ACE vuông tại A.
![]()
Mặt khác, ta có BC'=B'E=AB' nên tam giác AB'E vuông cân tại B'.
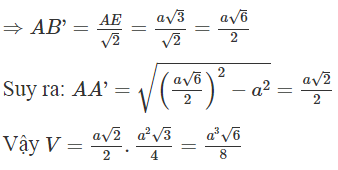
Câu 16:
Cho hình lăng trụ đứng ABC. A'B'C' có đáy là tam giác vuông và AB=BC=a,
AA' = , M là trung điểm của BC. Tính khoảng cách d của hai đường thẳng AM và B'C.
 Xem đáp án
Xem đáp án
Chọn C
Tam giác ABC vuông và AB=BC=a nên ΔABC chỉ có thể vuông tại B.
Ta có
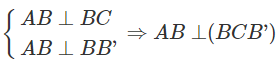
Kẻ
Tứ diện BAMN là tứ diện vuông
Câu 17:
Cho hình chóp S. ABCD có đáy là hình chữ nhật, AB = a, AD =
 Xem đáp án
Xem đáp án
Chọn B
Gọi R và r lần lượt là bán kính mặt cầu ngoại tiếp hình chóp S. BHD và tam giác BHD.
Ta có
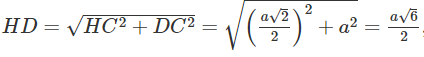
![]()
Áp dụng định lí Cô sin, ta có
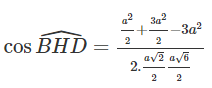
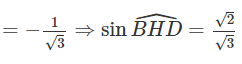
Diện tích tam giác BHD là
![]()
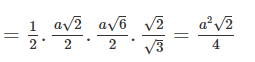
Do đó
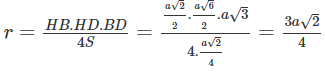
Gọi O là tâm đường tròn ngoại tiếp tam giác BHD và M là trung điểm SH. Mặt phẳng trung trực của SH cắt trục đường tròn ngoại tiếp tam giác BHD tại E. Khi đó E là tâm mặt cầu cần tìm.
Ta có:
![]()
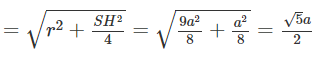
Câu 18:
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau,
OA=
 Xem đáp án
Xem đáp án
Chọn D
Từ giả thiết suy ra: ΔABC cân tại A có:
Gọi I là trung điểm của BC
Giả sử H là trực tâm của tam giác ABC.
Ta thấy
Vì ⇒ OB ⊥ AC và nên
Từ (1) và (2) suy ra
=> ΔAOI vuông cân tại O => H là trung điểm AI và
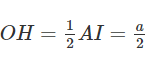
Khi đó:
Câu 19:
Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a. Gọi O và O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. Gọi M, N lần lượt là trung điểm của các cạnh B'C' và CD. Tính thể tích khối tứ diện OO'MN.
 Xem đáp án
Xem đáp án
Chọn D
Gọi P, Q lần lượt là trung điểm của BC và C'D'.
Ta có
![]()
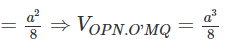
Ta lại có:
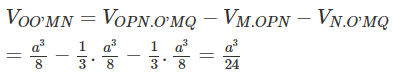
Câu 20:
Xét khối lăng trụ tam giác ABC. A'B'C'. Mặt phẳng đi qua C' và các trung điểm của AA', BB' chia khối lăng trụ thành hai phần có tỉ số thể tích bằng:
 Xem đáp án
Xem đáp án
Chọn B
Gọi E, F lần lượt là các trung điểm của AA' và BB' khi đó ta có:
Vậy mặt phẳng (C'EF) chia khối lăng trụ thành hai phần có tỉ số thể tích bằng