18 câu hỏi trắc nghiệm thuộc 80 câu trắc nghiệm Khối đa diện nâng cao phần 4 (có đáp án) - hamchoi.vn

80 câu trắc nghiệm Khối đa diện nâng cao (có đáp án)

80 câu trắc nghiệm Khối đa diện nâng cao phần 4 (có đáp án)

1604 lượt thi
18 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = $a \sqrt{10}$ . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60⁰. Tính thể tích V của khối chóp S.ABCD theo a.

A. $V = \frac{3 \sqrt{30} a^{3}}{8}$

B. $V = \frac{\sqrt{30} a^{3}}{4}$

C. $V = \frac{\sqrt{30} a^{3}}{12}$

D. $V = \frac{\sqrt{30} a^{3}}{8}$

Chọn D

Ta có

Gọi H là trung điểm AB thì $S H ⊥ (A B C D)$ , kẻ

ta có $\hat{S K H}$ là góc giữa (SBD) và (ABCD), do đó $\hat{S K H}$ = 60⁰

Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:

Câu 2:

Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy (ABCD). Biết côsin của góc tạo bởi mặt phẳng (SCD) và (ABCD) bằng $\frac{2 \sqrt{17}}{17}$ . Thể tích Vcủa khối chóp S.ABCD là:

A. $V = \frac{a^{3} \sqrt{13}}{6}$

B. $V = \frac{a^{3} \sqrt{17}}{6}$

C. $V = \frac{a^{3} \sqrt{17}}{2}$

D. $V = \frac{a^{3} \sqrt{13}}{2}$

Chọn A

Câu 3:

Khối chóp S.ABCD có đáy là hình thoi cạnh a, SA = SB = SC = a, cạnh SD thay đổi. Thể tích lớn nhất của khối chóp S.ABCD là:

A. $\frac{a^{3}}{2}$

B. $\frac{a^{3}}{8}$

C. $\frac{3 a^{3}}{8}$

D. $\frac{a^{3}}{4}$

Chọn D

Gọi I là tâm hình thoi ABCD, H là hình chiếu của S lên mặt phẳng (ABCD).

Ta có SA = SB = SC nên hình chiếu vuông góc của S xuống mặt phẳng (ABCD) trùng với tâm đường tròn ngoại tiếp ΔABC hay H ∈ BI

Khi đó tam giác SBD vuông tại S.

Giả sử SD = x.

Câu 4:

Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng:

A. $\frac{a \sqrt{2}}{2}$

B. $\frac{a \sqrt{3}}{4}$

C. $\frac{a \sqrt{2}}{17}$

D. $\frac{a \sqrt{6}}{4}$

Chọn C

Câu 5:

Hình lăng trụ đứng ABC.A'B'C' có diện tích đáy bằng 4, diện tích ba mặt bên lần lượt là 9, 18 và 10. Thể tích khối lăng trụ ABC.A'B'C' bằng:

A. $\sqrt[4]{1195}$

B. $\frac{\sqrt[4]{1195}}{12}$

C. $\sqrt{1195}$

D. $\frac{\sqrt{1195}}{12}$

Chọn D

Câu 6:

Cho hình lăng trụ ABC.A'B'C' có thể tích bằng 48cm³. Gọi M, N, P theo thứ tự là trung điểm các cạnh CC', BC và B'C', khi đó thể tích V của khối chóp A'.MNP là:

A. $\frac{16}{3} c m^{3}$

B. 8 $c m^{3}$

C. 24 $c m^{3}$

D. 12 $c m^{3}$

Chọn B

Câu 7:

Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = a. Gọi I là trung điểm của AC. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H thỏa mãn $\vec{B I} = 3 \vec{I H}$ . Góc giữa hai mặt phẳng (SAB) và (SBC) là 60 độ. Thể tích của khối chóp S.ABC là:

A. $V = \frac{a^{3}}{9}$

B. $V = \frac{a^{3}}{6}$

C. $V = \frac{a^{3}}{18}$

D. $V = \frac{a^{3}}{3}$

Chọn A

Cách 1:

Dễ thấy hai tam giác SAB và SAC bằng nhau (cạnh chung SA), gọi K là chân đường cao hạ từ A trong tam giác SAB

Từ giả thiết tam giác ABC vuông cân tại B ta được

Trong tam giác ICK vuông tại I có

Suy ra IK > IB.

Do nên tam giác BIK vuông tại K

Như vậy IK > IB (vô lý do IB là cạnh huyền).

TH2: $\hat{A K C} = 120^{o}$ tương tự phần trên ta có

Do

nên tam giác BIK vuông tại K và

Như vậy tam giác BKI đồng dạng với tam giác BHS suy ra:

Vậy thể tích của khối chóp S.ABC là

Câu 8:

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = $a \sqrt{2}$ . Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B', D', C'. Thể tích khối chóp S. AB'C'D' là:

A. $V = \frac{2 a^{3} \sqrt{3}}{9}$

B. $V = \frac{2 a^{3} \sqrt{2}}{3}$

C. $V = \frac{a^{3} \sqrt{2}}{9}$

D. $V = \frac{2 a^{3} \sqrt{3}}{3}$

Chọn C

Dựa vào giả thiết ta có B', C', D' lần lượt là hình chiếu của A lên SB, SC, SD.

Tam giác SAC vuông cân tại A nên C' là trung điểm của SC.

Trong tam giác vuông SAB' ta có:

Câu 9:

Cho khối tứ diện đều ABCD có thể tích là V. Gọi M, N, P, Q lần lượt là trung điểm của AC, AD, BD, BC. Thể tích khối chóp AMNPQ là:

A. $\frac{V}{6}$

B. $\frac{V}{3}$

C. $\frac{V}{4}$

D. $\frac{V \sqrt{2}}{3}$

Chọn C

Câu 10:

Cho hình lăng trụ tam giác đều ABC. A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60⁰, cạnh AB=a. Tính thể tích V của khối lăng trụ ABC. A'B'C'.

A. $V = \frac{\sqrt{3} a^{3}}{4}$

B. $V = \frac{3 a^{3}}{4}$

C. $V = \frac{3 \sqrt{3} a^{3}}{8}$

D. $V = \sqrt{3} a^{3}$

Chọn C

Gọi M là trung điểm của BC

$\Rightarrow$ AM $⊥$ BC (1)

Ta có

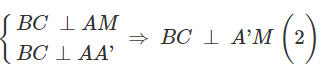
Mặt khác $(A B C) \cap (A' B C) = B C (3)$

$(A B C) \cap (A' B C) = B C (3)$

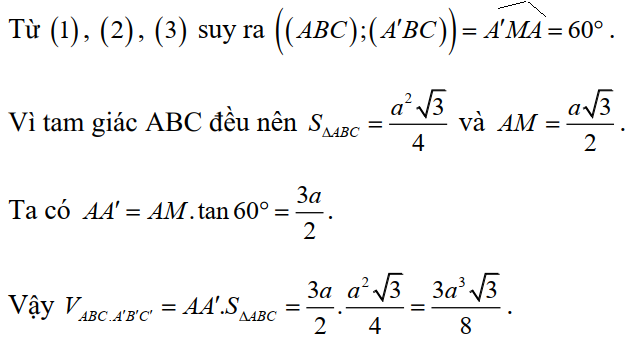
Câu 11:

Cho tứ diện SABC và hai điểm M, N lần lượt thuộc các cạnh SA, SB sao cho $\frac{S M}{A M} = \frac{1}{2}; \frac{S N}{B N} = 2$ . Mặt phăng (P) đi qua hai điểm M, N và song song với cạnh SC, cắt AC, BC lần lượt tại L, K. Tính tỉ số thể tích $\frac{V_{S C M N K L}}{V_{S A B C}}$ $\frac{S M}{A M} = \frac{1}{2}$ $\frac{S N}{B N} = 2$

A. $\frac{V_{S C M N K L}}{V_{S A B C}} = \frac{4}{9}$

B. $\frac{V_{S C M N K L}}{V_{S A B C}} = \frac{1}{3}$

C. $\frac{V_{S C M N K L}}{V_{S A B C}} = \frac{2}{3}$

D. $\frac{V_{S C M N K L}}{V_{S A B C}} = \frac{1}{4}$

Chọn A

Chia khối đa diện SCMNKL bởi mặt phẳng (NLC) được hai khối chóp N. SMLC và N. LKC. Vì SC song song với (MNKL) nên SC // ML //NK

Câu 12:

Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng $\frac{a}{6}$ Thể tích khối lăng trụ bằng

A. $\frac{3 a^{3} \sqrt{2}}{4}$

B. $\frac{3 a^{3} \sqrt{2}}{8}$

C. $\frac{3 a^{3} \sqrt{2}}{28}$

D. $\frac{3 a^{3} \sqrt{2}}{16}$

Chọn D

Gọi M là trung điểm của BC và H là hình chiếu của A trên A'M.

Ta có :

(do tính chất trọng tâm).

Xét tam giác vuông A'AM :

Suy ra thể tích lăng trụ ABC. A'B'C' là:

Câu 13:

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a và cạnh bên SA vuông góc với mặt phẳng đáy. Gọi E là trung điểm của cạnh CD. Biết thể tích của khối chóp S. ABCD bằng $\frac{a^{3}}{3}$ Tính khoảng cách từ A đến mặt phẳng (SBE).

A. $\frac{2 a}{3}$

B. $\frac{\sqrt{2} a}{3}$

C. $\frac{a}{3}$

D. $\frac{\sqrt{3} a}{3}$

Chọn A

Câu 14:

Cho khối chóp S. ABCD có đáy ABCD là tứ giác lồi, tam giác ABD đều cạnh a, tam giác BCD cân tại C và $\hat{B C D} = 120^{o}$ , $S A ⊥ (A B C D)$ và SA=a. Mặt phẳng (P) đi qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại M, N, P. Tính thể tích khối chóp S. AMNP.

A. $\frac{a^{3} \sqrt{3}}{42}$

B. $\frac{2 a^{3} \sqrt{3}}{21}$

C. $\frac{a^{3} \sqrt{3}}{14}$

D. $\frac{a^{3} \sqrt{3}}{12}$

Chọn A

Gọi O là trọng tâm tam giác đều ABD và I là trung điểm BD thì:

Tam giác ICD vuông I có

$\Rightarrow$ O và C đối xứng nhau qua đường thẳng BD

Tam giác SAC vuông tại A có SN. SC=SA²

Tam giác ABC có

và AC²=AB²+BC²

$\Rightarrow$ tam giác ABC vuông tại B

Lại có tam giác SAB vuông nên $A M ⊥ S B \Rightarrow$ M là trung điểm SB

Mặt khác

Câu 15:

Cho khối chóp tứ giác S. ABCD. Mặt phẳng đi qua trọng tâm các tam giác SAB,

SAC, SAD chia khối chóp này thành hai phần có thể tích là V₁ và V₂

(V₁ < V₂). Tính tỉ lệ $\frac{V_{1}}{V_{2}}$ .

A. $\frac{8}{27}$

B. $\frac{16}{81}$

C. $\frac{8}{19}$

D. $\frac{16}{75}$

Chọn C

Gọi G₁, G₂, G₃ lần lượt là trọng tâm các tam giác SAB, SAD, SAC.

Gọi I, J lần lượt là trung điểm của AB, AC thì

Qua G₁ dựng đường song song với AB, cắt SA, SB lần lượt tại M, N.

Qua N dựng đường song song với BC, cắt SC tại P.

Qua P dựng đường song song với CD, cắt SD tại Q.

$\Rightarrow$ Thiết diện của hình chóp S. ABCD khi cắt bới (G₁G₂G₃) là tứ giác MNPQ.

Câu 16:

Cho hình lăng trụ ABC. A'B'C' có đáy ABC là tam giác vuông tại A. cạnh BC=2a và $\hat{B' B C}$ nhọn. Biết (BCC'B') vuông góc với (ABC) và (ABB'A') tạo với (ABC) góc 45⁰. Thể tích của khối lăng trụ ABC. A'B'C' bằng:

A. $\frac{a^{3}}{\sqrt{7}}$

B. $\frac{3 a^{3}}{\sqrt{7}}$

C. $\frac{6 a^{3}}{\sqrt{7}}$

D. $\frac{a^{3}}{3 \sqrt{7}}$

Chọn B

Do ABC là tam giác vuông tại A, cạnh BC=2a và $\hat{A B C} = 60^{o}$ nên AB=a, AC= $\sqrt{3}$

Gọi H là hình chiếu vuông góc của B' lên BC $\Rightarrow$ H thuộc đoạn BC (do $\hat{B' B C}$ nhọn)

$\Rightarrow B H' ⊥ (A B C)$ (do (BCC'B') vuông góc với (ABC)).

Kẻ HK song song AC (K thuộc AB), $H K ⊥ A B$ (do ABC là tam giác vuông tại A).

Ta có ΔBB'H vuông tại H

Mặt khác HK song song AC

Từ (1), (2) và (3) suy ra:

Câu 17:

Cho khối lăng trụ ABC. A'B'C'. Gọi E là trọng tâm tam giác A'B'C' và F là trung điểm BC. Tính tỉ số thể tích giữa khối B'. EAF và khối lăng trụ ABC. A'B'C'.

A. $\frac{1}{4}$

B. $\frac{1}{8}$

C. $\frac{1}{5}$

D. $\frac{1}{6}$

Chọn D

Câu 18:

Cho hình chóp S. ABC có đường cao SA=2a, tam giác ABC vuông tại C, AB=2a, $\hat{C A B} = 30^{o}$ $\hat{C A B} = 30^{0}$ . Gọi H là hình chiếu của A trên SC, B' là điểm đối xứng của B qua mặt phẳng (SAC). Thể tích của khối chóp H. AB'B bằng:

A. $\frac{a^{3} \sqrt{3}}{7}$

B. $\frac{6 a^{3} \sqrt{3}}{7}$

C. $\frac{4 a^{3} \sqrt{3}}{7}$

D. $\frac{2 a^{3} \sqrt{3}}{7}$

Chọn D

Xét tam giác ABC ta có

Xét tam giác SAC ta có

Xét tam giác SAC ta có

Ta có:

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương