20 câu hỏi trắc nghiệm thuộc 80 câu trắc nghiệm Khối đa diện nâng cao phần 3 (có đáp án)

Câu 1:

Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc với nhau, biết OA=3, OB=4 và thể tích khối tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC) bằng:

A. 3

B. $\frac{\sqrt{41}}{12}$

C. $\frac{144}{\sqrt{41}}$

D. $\frac{12}{\sqrt{41}}$

Xem đáp án

Chọn D

Câu 2:

Cho hình chóp tứ giác đều S. ABCD. Mặt phẳng (P) chứa đường thẳng AC và vuông góc với mặt phẳng (SCD), cắt đường thẳng SD tại E. Gọi V và V₁ lần lượt là thể tích các khối chóp S.ABCD và D.ACE. Tính số đo góc tạo bởi mặt bên và mặt đáy của hình chóp S.ABCD biết V = 5 $V_{1}$

A. $60^{0}$

B. $120^{0}$

C. $45^{0}$

D. $90^{0}$

Xem đáp án

Chọn A

Gọi M là trung điểm CD. Góc tạo bởi mặt bên và mặt đáy là góc SMO

Đây là giao điểm cần tìm.

Xét tam giác vuông SOD.

Xét tam giác vuông SOM vuông tại O có

Câu 3:

mặt phẳng (SCD), cắt đường thẳng SD tại E. Gọi V và V₁ lần lượt là thể tích các khối chóp S.ABCD và D.ACE. Tính số đo góc tạo bởi mặt bên và mặt đáy của hình chóp S.ABCD biết V = 5 V 1

A. $\frac{105 \sqrt{3}}{2} (c m^{3})$

B. $\frac{35 \sqrt{3}}{2} (c m^{3})$

C. $24 \sqrt{3} (c m^{3})$

D. $8 \sqrt{3} (c m^{3})$

Xem đáp án

Chọn D

Gọi H là hình chiếu vuông góc của S xuống mặt phẳng (ABC) và I, J, K là hình chiếu vuông góc của H lên các cạnh BC, CA, AB

Mà các mặt bên tạo với đáy 1 góc 60⁰ nên

=> ΔSHJ = ΔSHI = ΔSHK (cạnh góc vuông – góc nhọn)

=> HI=HJ=HK => H là tâm đường tròn nội tiếp tam giác ABC

Mặt khác:

Tam giác SHI vuông tại H có SH = HI . tan 60⁰ = $2 \sqrt{2}$

Khi đó:

Câu 4:

Cho khối lăng trụ tam giác đều ABC. A'B'C' có cạnh đáy là a và khoảng cách từ A đến mặt phẳng (A'BC) bằng $\frac{a}{2}$ . Thể tích của khối lăng trụ bằng:

A. $\frac{3 \sqrt{2} a^{3}}{12}$

B. $\frac{\sqrt{2} a^{3}}{16}$

C. $\frac{3 \sqrt{2} a^{3}}{16}$

D. $\frac{3 \sqrt{2} a^{3}}{48}$

Xem đáp án

Chọn C

Gọi I là trung điểm của BC và H là hình chiếu vuông góc của A trên A'I. Khi đó ta có:

Trong tam giác vuông AA'I ta có:

Câu 5:

Cho lăng trụ tam giác đều ABC. A'B'C' có tất cả các cạnh đều bằng a. Khoảng cách giữa hai đường thẳng BC và AB' bằng:

A. $\frac{a \sqrt{2}}{17}$

B. $\frac{a \sqrt{3}}{2}$

C. $\frac{a \sqrt{7}}{4}$

D. $\frac{a \sqrt{2}}{2}$

Xem đáp án

Chọn A

Gọi I và H lần lượt là hình chiếu vuông góc của A' trên B'C' và AI.

Câu 6:

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA = a và SA vuông góc với đáy. Gọi M là trung điểm SB, N thuộc cạnh SD sao cho SN = 2ND. Tính thể tích V của khối tứ diện ACMN.

A. $V = \frac{a^{3}}{8}$

B. $V = \frac{a^{3}}{6}$

C. $V = \frac{a^{3}}{36}$

D. $V = \frac{a^{3}}{12}$

Xem đáp án

Chọn D

Thể tích khối chóp S. ABCD là:

Thể tích tứ diện SMNC là:

Thể tích tứ diện NACD là:

Thể tích tứ diện MABC là:

Thể tích tứ diện SAMN là:

Mặt khác ta có:

Suy ra:

Câu 7:

Cho khối hộp chữ nhật ABCD. A'B'C'D' có thể tích bằng 2110. Biết (MNP), DN=3ND', CP=2C'P như hình vẽ. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng:

A. $\frac{5275}{6}$

B. $\frac{8440}{9}$

C. $\frac{7485}{18}$

D. $\frac{5275}{12}$

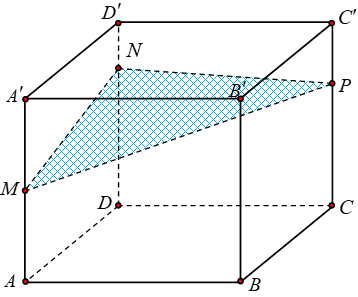
Xem đáp án

Chọn A

Gọi Q là giao điểm của mặt phẳng (MNP) với BB'.

Câu 8:

Xét tứ diện ABCD có các cạnh AB=BC=CD=DA=1 và AC, BD thay đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD bằng:

A. $\frac{2 \sqrt{3}}{27}$

B. $\frac{4 \sqrt{3}}{27}$

C. $\frac{2 \sqrt{3}}{9}$

D. $\frac{4 \sqrt{3}}{9}$

Xem đáp án

Chọn A

Gọi M, N lần lượt là trung điểm của BD, AC. Đặt BD = 2x, AC = 2y (x, y > 0).

Câu 9:

Cho khối lăng trụ tam giác ABC. A'B'C'. Gọi M, N lần lượt là trung điểm của BB' và CC'. Mặt phẳng (AMN) chia khối lăng trụ thành hai phần. Gọi V₁ là thể tích của khối đa diện chứa đỉnh B' và V₂ là thể tích khối đa diện còn lại. Tính tỉ số $\frac{V_{1}}{V_{2}}$

A. $\frac{V_{1}}{V_{2}} = \frac{7}{2}$

B. $\frac{V_{1}}{V_{2}} = 2$

C. $\frac{V_{1}}{V_{2}} = \frac{1}{3}$

D. $\frac{V_{1}}{V_{2}} = \frac{5}{2}$

Xem đáp án

Chọn B

Gọi K là trung điểm của AA' và V, V_ABC.KMN, V_A.KMN lần lượt là thể tích khối lăng trụ ABC. A'B'C' khối lăng trụ ABC. KMN và thể tích khối chóp A. MNK. Khi đó

Câu 10:

Xét tứ diện ABCD có các cạnh AC=CD=DB=BA=2 và AD, BC thay đổi. Giá trị lớn nhất của thể tích tứ diện ABCD bằng:

A. $\frac{16 \sqrt{3}}{9}$

B. $\frac{32 \sqrt{3}}{27}$

C. $\frac{16 \sqrt{3}}{27}$

D. $\frac{32 \sqrt{3}}{9}$

Xem đáp án

Chọn C

Gọi M, N lần lượt là trung điểm AD và BC.

Theo giả thiết ta có: ABD và ACD là các tam giác cân có M là trung điểm của AD nên:

Và có BM=CM => ΔMBC cân tại M

Trong tam giác ΔMBC có MN vừa là đường cao vừa là trung tuyến nên

Khi đó diện tích tam giác ΔMBC là:

Thể tích tứ diện ABCD là:

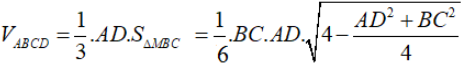
Đặt AD = 2x, BC = 2y ta có:

= $\frac{16 \sqrt{3}}{27}$

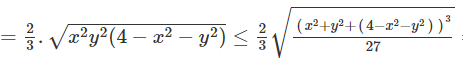
Dấu bằng xảy ra khi: $x^{2} = y^{2} = \sqrt{4 - x^{2} - y^{2}}$

$x^{2} = y^{2} = \sqrt{4 - x^{2} - y^{2}}$

Câu 11:

Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy, $A B = a; B C = a \sqrt{2}; S C = 2 a v à \hat{A S C} = 60^{o}$ . Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ABC

A. R = a

B. $R = \frac{a \sqrt{3}}{2}$

C. $R = a \sqrt{3}$

D. $R = a^{2}$

Xem đáp án

Chọn A

Ta có:

Do đó

vuông tại B.

Gọi P là trung điểm của cạnh AC thì P là tâm đường tròn ngoại tiếp ΔABC.

Gọi O là trung điểm của cạnh SC $\Rightarrow$ OS = OC

Ta có OP // SA mà

Do đó OP là trục đường tròn ngoại tiếp ΔABC $\Rightarrow$ OA=OB=OC.

Như vậy

Câu 12:

Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, SC hợp với đáy một góc 30⁰, M là trung điểm của AC. Tính thể tích khối chóp S. BCM.

A. $\frac{\sqrt{3} a^{3}}{48}$

B. $\frac{\sqrt{3} a^{3}}{31}$

C. $\frac{\sqrt{3} a^{3}}{39}$

D. $\frac{\sqrt{3} a^{3}}{24}$

Xem đáp án

Chọn A

Gọi H là trung điểm của AB. Theo bài ra:

Xét tam giác SCH ta có:

Câu 13:

Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của hình chóp tam giác S. ABC sao cho $\frac{S M}{M A} = \frac{1}{2}, \frac{S N}{N B} = 2$ Mặt phẳng (α) qua MN và song song với SC chia khối chóp thành 2 phần. Gọi V₁ là thể tích của khối đa diện chứa A, V₂ là thể tích của khối đa diện còn lại. Tính tỉ số $\frac{V_{1}}{V_{2}}$ $\frac{V_{1}}{V_{2}}$

A. $\frac{V_{1}}{V_{2}} = \frac{4}{5}$

B. $\frac{V_{1}}{V_{2}} = \frac{5}{4}$

C. $\frac{V_{1}}{V_{2}} = \frac{5}{6}$

D. $\frac{V_{1}}{V_{2}} = \frac{6}{5}$

Xem đáp án

Chọn B

Trong mặt phẳng (SAC) dựng MP song song với SC cắt AC tại P. Trong mặt phẳng (SBC) dựng NQ song song với SC cắt BC tại Q. Gọi D là giao điểm của MN và PQ. Dựng ME song song với AB cắt SB tại E (như hình vẽ).

Ta thấy:

Suy ra N là trung điểm của BE và DM, đồng thời

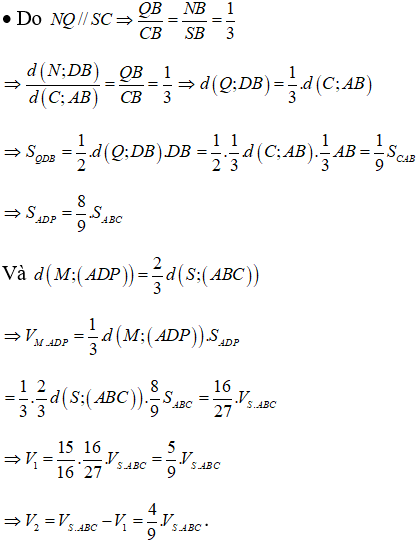
Vậy $\frac{V_{1}}{V_{2}} = \frac{5}{4}$

Câu 14:

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, biết SC = $a \sqrt{3}$ . Gọi M, N, P, Q lần lượt là trung điểm các cạnh SB, SD, CD, BC. Tính thể tích khối chóp AMNPQ

A. $\frac{a^{3}}{3}$

B. $\frac{a^{3}}{4}$

C. $\frac{a^{3}}{8}$

D. $\frac{a^{3}}{12}$

Xem đáp án

Chọn C

Câu 15:

Cho hình chóp tứ giác đều S. ABCD, M là trung điểm của SC. Mặt phẳng (P) qua AM và song song với BD cắt SB, SD tại N, K. Tính tỉ số thể tích của khối S. ANMK và khối chóp S.ABCD.

A. $\frac{2}{9}$

B. $\frac{1}{3}$

C. $\frac{1}{2}$

D. $\frac{3}{5}$

Xem đáp án

Chọn B

Câu 16:

Cho khối hộp ABCD. A'B'C'D' có đáy là hình chữ nhật với $A B = \sqrt{3}; A D = \sqrt{7}$ . Hai mặt bên (ABB'A') và (ADD'A') cùng tạo với đáy góc 45⁰, cạnh bên của hình hộp bằng 1 (hình vẽ). Thể tích khối hộp là:

A. $\sqrt{7}$

B. $3 \sqrt{3}$

C. 5

D. $7 \sqrt{7}$

Xem đáp án

Chọn A

Gọi H là hình chiếu vuông góc của A' lên mặt phẳng (ABCD);

Theo giả thiết, ta có

$\Rightarrow$ ΔHKA' = ΔHIA' HI = HK

$\Rightarrow$ tứ giác AIHK là hình vuông cạnh a, (a>0) $\Rightarrow$ AH = $a \sqrt{2}$

Tam giác A'HK vuông cân tại H có HK = HA' = a

Tam giác AHA' vuông tại H có AA'² = AH² + A'H²

Câu 17:

Cho hình chóp S. ABC có SA, SB, SC đôi một vuông góc với nhau và SA=SB=SC=a. Sin của góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:

A. $\frac{\sqrt{6}}{3}$

B. $\frac{\sqrt{2}}{2}$

C. $\frac{1}{\sqrt{3}}$

D. $\frac{2}{\sqrt{3}}$

Xem đáp án

Chọn C

Trong tam giác ABC kẻ đường cao AK và CF và nên E là trực tâm tam giác ABC.

Ta có:

Ta có CE là hình chiếu của SC lên mặt phẳng (ABC).

Ta có tam giác SCF vuông tại S nên

Mặt khác tam giác SAB vuông tại S nên:

Câu 18:

Cho tứ diện đều có cạnh bằng 3. M là một điểm thuộc miền trong của khối tứ diện tương ứng. Tính giá trị lớn nhất của tích các khoảng cách từ điểm M đến bốn mặt của tứ diện đã cho.

A. 36

B. $\frac{9}{64}$

C. $\sqrt{6}$

D. $\frac{\sqrt{6}}{4}$

Xem đáp án

Chọn B

Gọi r₁, r₂, r₃, r₄ là khoảng cánh từ điểm M đến bốn mặt của tứ diện.

Gọi S là diện tích một mặt của tứ diện

Đường cao của tứ diện là

Thể tích của tứ diện là

Mặt khác, ta có:

Câu 19:

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Biết khoảng cách giữa hai đường thẳng BC và SM bằng $\frac{a \sqrt{3}}{4}$ . Tính thể tích của khối chóp đã cho theo a.

A. $\frac{a^{3} \sqrt{3}}{4}$

B. $\frac{a^{3} \sqrt{3}}{2}$

C. $\frac{a^{3} \sqrt{3}}{6}$

D. $\frac{a^{3} \sqrt{3}}{12}$

Xem đáp án

Chọn C

Gọi N là trung điểm của AB $\Rightarrow$ BC // (SMN)

Suy ra d (BC, SM) = d (BC,(SMN))=d (B, (SMN)) = d (A, (SMN)).

Dựng AH vuông góc với SN tại H

Lại có, trong tam giác vuông SAN:

Câu 20:

Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng $\frac{a \sqrt{3}}{4}$ . Tính thể tích V của khối lăng trụ ABC.A'B'C'

A. $V = \frac{a^{3} \sqrt{3}}{6}$

B. $V = \frac{a^{3} \sqrt{3}}{3}$

C. $V = \frac{a^{3} \sqrt{3}}{24}$

D. $V = \frac{a^{3} \sqrt{3}}{12}$

Xem đáp án

Chọn D

CHỌN BỘ SÁCH BẠN MUỐN XEM

80 câu trắc nghiệm Khối đa diện nâng cao (có đáp án)

80 câu trắc nghiệm Khối đa diện nâng cao phần 3 (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương