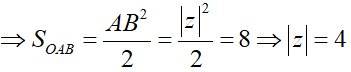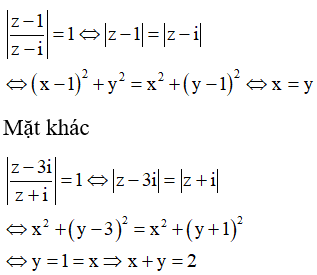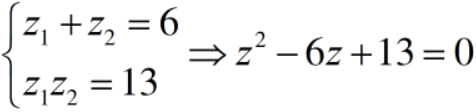Bài tập Số phức cơ bản, nâng cao có lời giải (P2)
-
1909 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Phần ảo của số phức là:
 Xem đáp án
Xem đáp án
Đáp án C
Chú ý: phần ảo của số phức z = a+bi là b, không phải là bi
Câu 4:
Cho số phức z thỏa mãn . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức . Tính môđun của số phức w= M+mi.
 Xem đáp án
Xem đáp án
Đáp án B
Đặt ![]() suy ra tập hợp các điểm M(z)= (x;y) là đường tròn (C) có tâm I(3;4) và bán kính R= .
suy ra tập hợp các điểm M(z)= (x;y) là đường tròn (C) có tâm I(3;4) và bán kính R= .
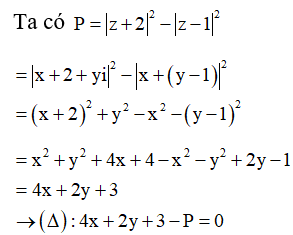
Ta cần tìm P sao cho đường thẳng và đường tròn (C) có điểm chung
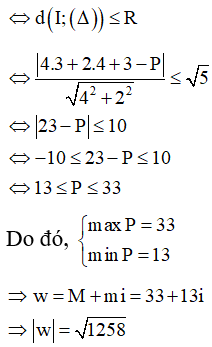
Câu 5:
Biết và là hai nghiệm của phương trình Khi đó giá trị của là
 Xem đáp án
Xem đáp án
Đáp án B
PT có 2 nghiệm:
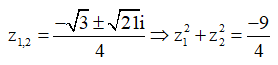
Câu 7:
Cho số phức z thỏa mãn .
Tìm giá trị lớn nhất của biểu thức .
 Xem đáp án
Xem đáp án
Đáp án B
Ta có 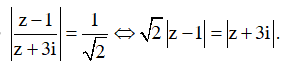
Gọi M là điểm biểu diễn số phức, tập hợp điểm biểu diễn số phức z là đường tròn có phương trình
![]()
![]()
A(0;-1), B(4;7) lần lượt biểu diễn 2 số phức ![]()
Ta có ![]() nên AB là bán kính đường tròn (C)
nên AB là bán kính đường tròn (C)
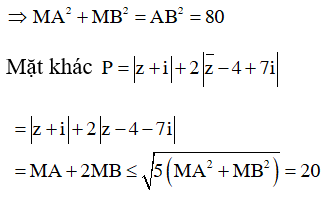
Dấu “=” xảy ra khi MB=2MA
Vậy maxP= 20
Câu 8:
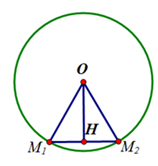
Cho hai số phức có điểm biểu diễn lần lượt là cùng thuộc đường tròn có phương trình và .Tính giá trị biểu thức
 Xem đáp án
Xem đáp án
Đáp án D
thuộc đường tròn (T) có tâm O(0;0) và bán kính R=1

Câu 9:
Phương trình bậc hai nào sau đây có nghiệm là 1+2i ?
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Cách 1: Giải các phương trình bậc hai ẩn z ở các đáp án, đáp án nào có nghiệm z = 1+2i thì chọn đáp án đó.
Cách 2: Thay nghiệm z = 1+2i vào các phương trình ở các đáp án. Đáp án nào thỏa mãn thì chọn đáp án đó.
Cách giải:
+) Xét phương trình:
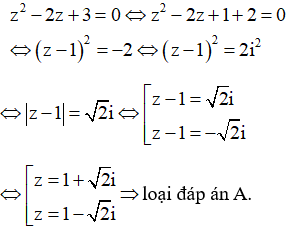
+) Xét phương trình:

+) Xét phương trình:
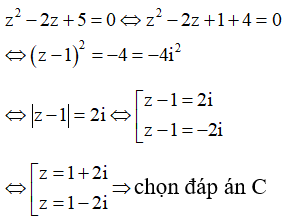
Câu 10:
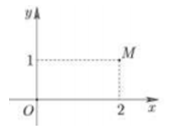
Trong hình vẽ bên, điểm M biểu diễn số phức z. Số phức là:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Cho điểm M(a;b) biểu diễn số phức ![]()
Cách giải:
Ta có M(2;1) biểu diễn số phức ![]()
Câu 11:
Cho số phức z=a+bi (a,b là các số thực) thỏa mãn .
Tính giá trị của biểu thức T=
 Xem đáp án
Xem đáp án
Đáp án C.
Phương pháp giải: Lấy môđun hai vế để tìm ,thế ngược lại để tìm số phức z
Lời giải:
Ta có ![]()
Lấy môđun 2 vế, ta được ![]()
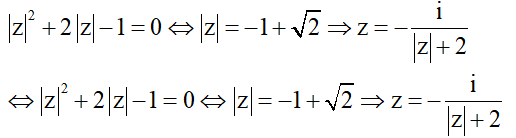
Vậy ![]()
Câu 12:
Gọi là hai nghiệm phức của phương trình trong đó là số phức có phần ảo âm.
Tìm số phức .
 Xem đáp án
Xem đáp án
Đáp án B.
Phương pháp giải: Giải phương trình bậc hai tìm nghiệm phức
Lời giải:
Ta có:
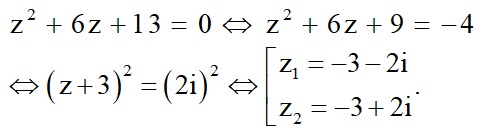
Vậy ![]()
Câu 13:
Cho số phức z=3+2i. Tính .
 Xem đáp án
Xem đáp án
Đáp án B.
Phương pháp giải: Số phức z=a+bi có môđun là
Lời giải: Ta có
![]()
Câu 14:
Cho hai số phức thỏa mãn và .
Tìm giá trị lớn nhất của biểu thức
 Xem đáp án
Xem đáp án
Đáp án A.
Phương pháp giải:
Đưa về biện luận vị trí giữa hai điểm thuộc đường tròn để khoảng cách của chúng lớn nhất
Lời giải:
Ta có ![]()
![]()
Và 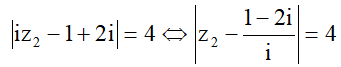
![]()
Đặt 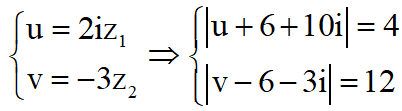
và ![]()
Tập hợp điểm M biểu diễn số phức u là đường tròn ![]() tâm
tâm
Tập hợp điểm N biểu diễn số phức v là đường tròn ![]() tâm
tâm
Khi đó ![]()
Câu 15:
Cho số phức z thỏa mãn .Tính môđun của số phức z
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp giải:
Tìm số phức z bằng phép chia số phức, sau đó tính môđun hoặc bấm máy tính
Lời giải: Ta có
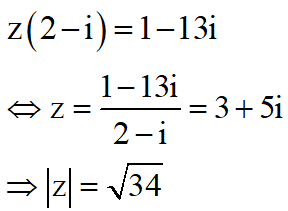
Câu 16:
Số phức thỏa mãn và là số thực.
Giá trị của biểu thức S=a+2b bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp giải:
Đặt z=a+bi thực hiện yêu cầu bài toán, chú ý số phức là số thực khi phần ảo bằng 0
Lời giải:
Ta có:
Khi đó
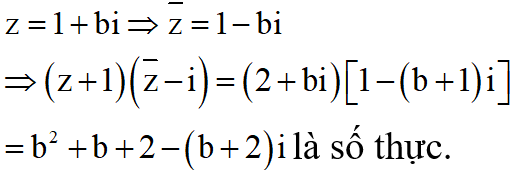
Khi và chỉ khi
Vậy S=a+2b= -3
Câu 17:
Cho số phức w và hai số thực a, b. Biết và là hai nghiệm phức của phương trình .
Tìm giá trị
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp giải:
Đặt số phức w, biến đổi về z và sử dụng hệ thức Viet cho phương trình bậc hai
Lời giải:
Đặt ![]()
suy ra 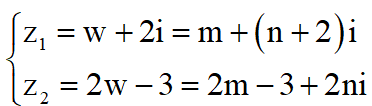
Ta có ![]() là số thực
là số thực

Lại có:
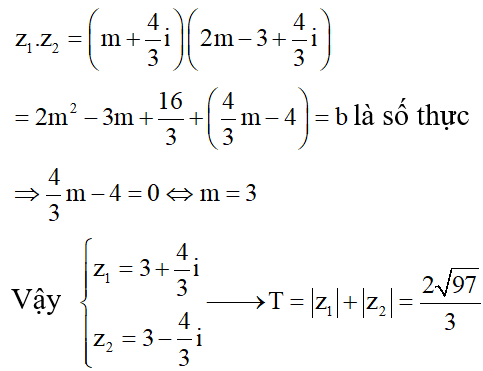
Câu 18:
Cho số phức z thỏa mãn .
Tìm giá trị lớn nhất của biểu thức
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp giải:
Gọi số phức, áp dụng bất đẳng thức Bunhiacopxki để tìm giá trị lớn nhất
Lời giải:
Cách 1. Gọi ![]()
Và A(-1;0), B(1;0)
Ta có ![]()
M thuộc đường tròn đường kính AB
![]()
Khi đó, theo Bunhiacopxki, ta có
![]()
Vậy giá trị lớn nhất của biểu thức maxT=
Cách 2. Đặt ![]()
![]()
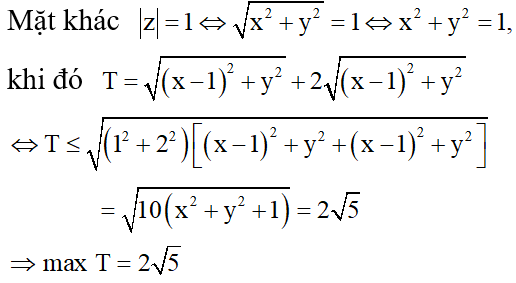
Câu 19:
Cho số phức z thỏa mãn ![]()
Tìm môđun của số phức z.
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Gọi ![]()
Sử dụng định nghĩa hai số phức bằng nhau.
Cách giải
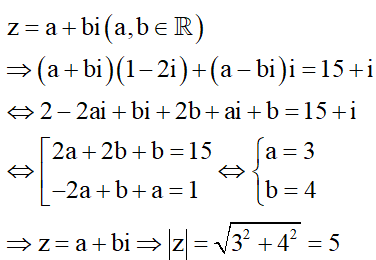
Câu 20:
Gọi là nghiệm phức có phần ảo âm của phương trình .
Tìm tọa độ điểm biểu diễn cho số phức trong mặt phẳng phức?
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
+) Tìm bằng cách giải phương trình
+) Thay vừa tìm được tính
+) Số phức z=a+bi có điểm biểu diễn là M(a;b)
Cách giải
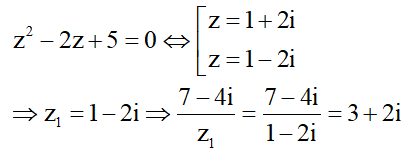
Câu 21:
Điểm A trong hình vẽ bên dưới biểu diễn cho số phức z.
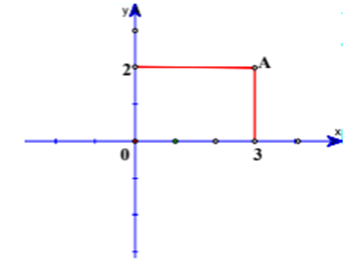
Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Điểm M(a;b) là điểm biểu diễn cho số phức z=a+bi có phần thực là a và phần ảo là b.
Cách giải
A(3;2) là điểm biểu diễn cho số phức z=3+2i có phần thực là 3, phần ảo là 2.
Câu 22:
Cho số phức thỏa mãn .
Gọi và số phức w=m+ni. Tính .
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Chia cả 2 vế cho và suy ra đường biểu diễn của số phức z
Cách giải
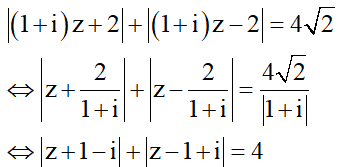
![]() Tập hợp các điểm z là elip có độ dài trục lớn là 2a=4
Tập hợp các điểm z là elip có độ dài trục lớn là 2a=4 ![]() a=2
a=2
và hai tiêu điểm ![]()
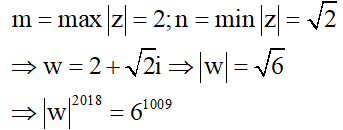
Câu 23:
Cho số phức z=a+bi với a,b là các số thực bất kỳ. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án B.
Đáp án A. Phần ảo của số phức z là b nên A sai.
Đáp án B. Ta có ![]() nên B đúng.
nên B đúng.
Đáp án C. Ta có ![]() là số thực khi b=0 nên C sai.
là số thực khi b=0 nên C sai.
Đáp án D. Ta có ![]() nên D sai.
nên D sai.
Câu 25:
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và (1+i)z.
Tính biết diện tích tam giác OAB bằng 8.
 Xem đáp án
Xem đáp án
Đáp án D
HD: Ta có
![]()
Suy ra ∆OAB vuông cân tại A