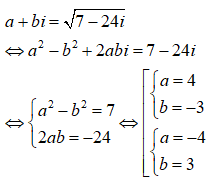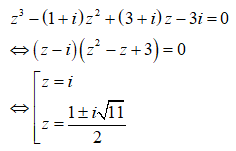Bài tập Số phức cơ bản, nâng cao có lời giải (P6)
-
1910 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho số phức z thỏa mãn (1-3i)z+1+i=-z. Môđun của số phức w=13z+2i có giá trị bằng:
 Xem đáp án
Xem đáp án
Đáp án C.
Ta có:
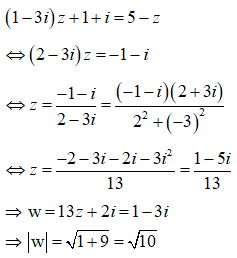
Câu 2:
Cho số phức z=(1-2i)(4-3i)-2+8i. Cho các phát biểu sau:
(1) Modun của z là một số nguyên tố
(2) z có phần thực và phần ảo đều âm
(3) z là số thuần thực
(4) Số phức liên hợp của z có phần ảo là 3i
Số phát biểu sai là:
 Xem đáp án
Xem đáp án
Đáp án B.
Ta có: z = (1-2i)(4-3i)-2+8i = -4-3i
Phần thực: –4, phần ảo: –3
![]()
Hai ý (3) và (4) sai.
Câu 3:
Trên mặt phẳng tọa độ Oxy. Cho tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện . Phát biểu nào sau đây là sai:
 Xem đáp án
Xem đáp án
Đáp án D.
Gọi ![]()
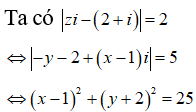
Vậy tập hợp điểm biểu diễn các số phức là đường tròn tâm I(1;-2) và bán kính R=5
Bình luận: Bài toán này ta dễ dàng nhận ra bằng phương pháp loại trừ nhất định 2 đáp án B và C đúng.
Mặt khác ![]()
Vậy biểu diễn hình học của z không thể là hình tròn:
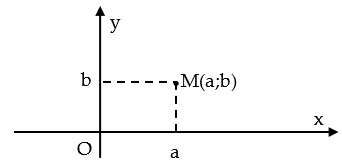
Biểu diễn hình học của số phức.
Số phức z=a+bi được biểu diễn bởi điểm M(a;b) trong mặt phẳng Oxy.
Câu 4:
Gọi T là tập hợp các số phức z thỏa mãn và . Gọi lần lượt là các số phức có môdun nhỏ nhất và lớn nhất. Tìm số phức
 Xem đáp án
Xem đáp án
Đáp án A.
Do ![]() nên tập hợp điểm M là các điểm nằm ngoài đường tròn
nên tập hợp điểm M là các điểm nằm ngoài đường tròn ![]() và nằm trong đường tròn
và nằm trong đường tròn 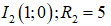
Dựa vào hình vẽ ta chứng minh được ![]()
Khi đó ![]()
Câu 5:
Cho số phức z thỏa mãn .
Gọi M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức .
Tính M.m
 Xem đáp án
Xem đáp án
Chọn D.
Dạng tổng quát: Cho số phức z thỏa mãn ![]() . Tính Min, Max của
. Tính Min, Max của ![]() .
.
Ta có: 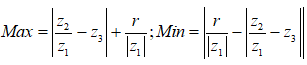
Áp dụng Công thức trên với ![]()
Ta được: Max=6; Min=4
Câu 7:
Gọi z1 và z2 là 2 nghiệm phức của phương trình: .
Tính giá trị của biểu thức
 Xem đáp án
Xem đáp án
Chọn C.
Ta có: ![]() do đó phương trình
do đó phương trình
![]() hay
hay ![]()
![]()
Câu 8:
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
 Xem đáp án
Xem đáp án
Chọn C.
Đặt ![]() ;
;
suy ra ![]()
Từ giả thiết, ta có:
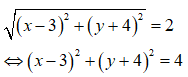
Tập hợp điểm biểu diễn các số phức z là đường tròn tâm I(3;-4) bán kính R=2.
Câu 11:
Cho các số phức được biểu diễn trong mặt phẳng tọa độ Oxy là M,N,P, các điểm này lần lượt là trung điểm của ba cạnh tam giác EFH. Tọa độ trọng tâm G của tam giác EFH là:
 Xem đáp án
Xem đáp án
Chọn D.
M(1;0), N(2;2), P(-1;3) là điểm biểu diễn các số phức trên .
Hai tam giác EFH và MNP có 3 trung tuyến trùng nhau từng đôi một nên có cùng trọng tâm G.
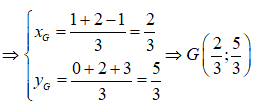
Câu 13:
Cho số phức z, biết .
Tìm số phức liên hợp của số phức w=3z-3i
 Xem đáp án
Xem đáp án
Chọn D.
Giả sử z=a+bi với a,b
Thay vào biểu thức ta được:
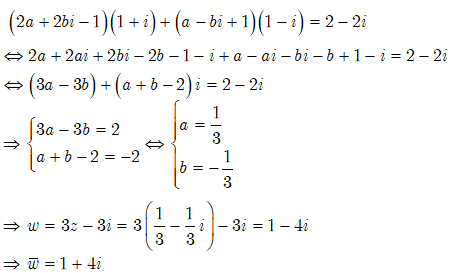
Câu 14:
Tính căn bậc hai của
 Xem đáp án
Xem đáp án
Chọn C.
Gọi ![]() là một căn bậc hai của , ta có:
là một căn bậc hai của , ta có:
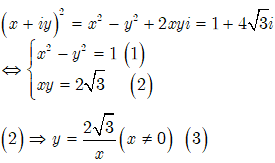
Thay (3) vào (1) ta được:
![]()
![]() (nhận) hoặc (loại)
(nhận) hoặc (loại)
* Với x=2 thì y=
* Với x=-2 thì y=-
Vậy căn bậc hai của là
Câu 15:
Trên mặt phẳng tọa độ Oxy . Cho tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện . Phát biểu nào sau đây là sai:
 Xem đáp án
Xem đáp án
Chọn D.
Gọi ![]()
Ta có
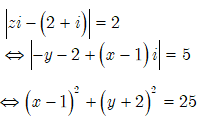
Vậy tập hợp điểm biểu diễn các số phức z là đường tròn tâm I(1;-2) và bán kính R=5
Câu 16:
Gọi S là tập hợp các số phức z thỏa mãn và . Kí hiệu là hai số phức thuộc S và là những số phức có môđun lần lượt nhỏ nhất và lớn nhất. Tính giá trị của biểu thức .
 Xem đáp án
Xem đáp án
Chọn C.
· ![]()
· Dấu “=” xảy ra khi:
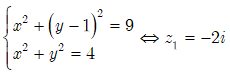
· 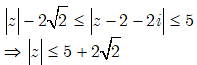
· Dấu “=” xảy ra khi:
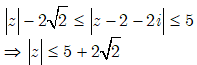
Câu 17:
Mệnh đề nào dưới đây là sai ?
 Xem đáp án
Xem đáp án
Chọn C.
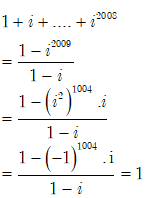 (Câu A đúng)
(Câu A đúng)
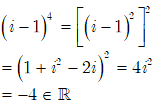 (Câu B đúng)
(Câu B đúng)
Đặt ![]() .
.
Do đó ![]() câu C sai
câu C sai
![]() (câu D đúng)
(câu D đúng)
Câu 18:
Trong mặt phẳng Oxy, M,N,P là tọa độ điểm biểu diễn của số phức
Tọa độ trực tâm H của tam giác MNP là:
 Xem đáp án
Xem đáp án
Chọn D.
M(-5;6), N(-4;-1), P(4;3)
Gọi H(x;y) là trực tâm MNP, ta có:
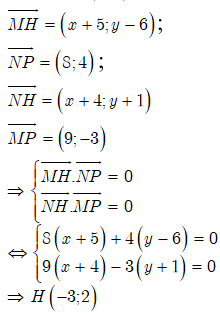
Câu 19:
Cho số phức z=x+yi với x, y là các số thực không âm thỏa mãn và biểu thức . Giá trị lớn nhất và giá trị nhỏ nhất của P lần lượt là:
 Xem đáp án
Xem đáp án
Chọn A.
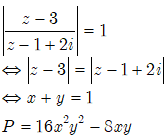
Đặt 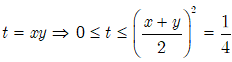

Câu 23:
Tập hợp các điểm biểu diễn số phức z sao cho là một số thuần ảo.
Là một đường tròn tâm I(a;b). Tính tổng a + b
 Xem đáp án
Xem đáp án
Chọn C.
Giả sử ![]() có điểm M(x;y) biểu diễn z trên mặt phẳng (Oxy).
có điểm M(x;y) biểu diễn z trên mặt phẳng (Oxy).
Khi đó
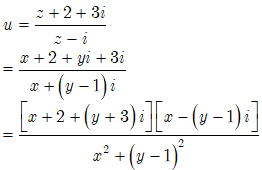
Từ số bằng: ![]() ; u là số thuần ảo khi và chỉ khi:
; u là số thuần ảo khi và chỉ khi:
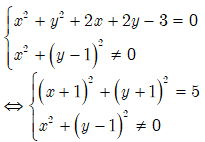
Kết luận: Vậy tập hợp các điểm biểu diễn của z là một đường tròn tâm I(-1;-1), bán kính R=, loại đi điểm (0;1).
Câu 24:
Trong mặt phẳng tọa độ Oxy, cho ba điểm M,N,P là điểm biểu diễn của 3 số phức: .Với giá trị nào của x thì tam giác MNP vuông tại P?
 Xem đáp án
Xem đáp án
Chọn B.
Ta có 3 điểm M(8;3), N(1;4), P(5;x)
![]()
Để MNP vuông tại P
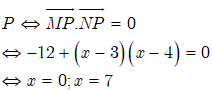
Câu 25:
Cho số phức z thỏa mãn .
Giá trị nhỏ nhất của là:
 Xem đáp án
Xem đáp án
Chọn B.
Gọi số phức cần tìm là ![]() .
.
Khi đó trừ giả thiết ta có