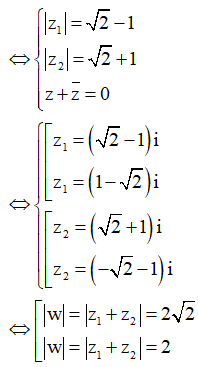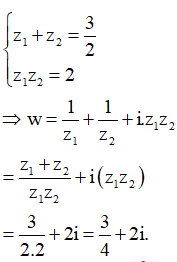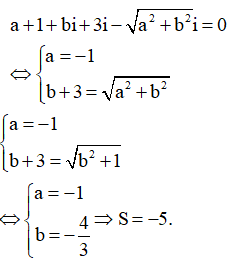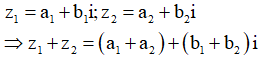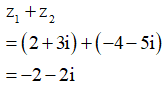Bài tập Số phức cơ bản, nâng cao có lời giải (P5)
-
1912 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho số phức z thỏa mãn .
Tính GTLN của
 Xem đáp án
Xem đáp án
Đáp án A
Cho số phức ![]() ,S(x;y) là điểm biểu diễn của z trên hệ trục tọa độ Oxy
,S(x;y) là điểm biểu diễn của z trên hệ trục tọa độ Oxy
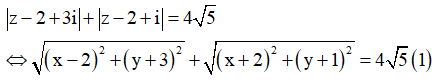
Lấy các điểm A(2;-3),B(-2;-1)
Phương trình ![]()
![]() Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2;-3),B(-2;-1) và có độ dài trục lớn là
Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2;-3),B(-2;-1) và có độ dài trục lớn là ![]()
Lấy M(4;-4).
Dễ dàng kiểm tra được 
Suy ra, M là một đỉnh và nằm trên trục lớn của elip (E).
Gọi I là trung điểm AB
![]() I(0;-2) ,N là điểm đối xứng của M qua I.
I(0;-2) ,N là điểm đối xứng của M qua I.
Khi đó, với mọi điểm ![]()
![]() khi và chỉ khi S trùng N
khi và chỉ khi S trùng N
![]() khi và chỉ khi SN(-4;0)
khi và chỉ khi SN(-4;0)
![]() z=-4
z=-4
Câu 6:
Nghiệm phức có phần ảo dương của phương trình là . Tính
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp :
Tìm nghiệm phức có phần ảo dương của phương trình ![]() bằng MTCT.
bằng MTCT.
Cách giải:
Sử dụng MTCT ta tính được nghiệm phức có phần ảo dương của phương trình trên là
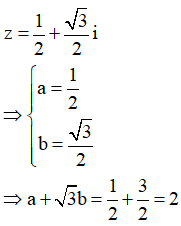
Câu 7:
Cho hai số phức thỏa mãn .
Gọi M, N là các điểm biểu diễn cho và .
Biết . Tính ?
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp: Tìm các điểm biểu diễn và đưa về bài toán hình học.
Cách giải :
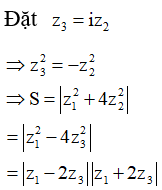
M, N là các điểm biểu diễn cho
![]()
Gọi P là điểm biểu diễn cho và Q là điểm biểu diễn cho
Ta có N là trung điểm của OP và P, Q đối xứng nhau qua O
Khi đó S=MP.MQ
Áp dụng định lí Cosin trong có:
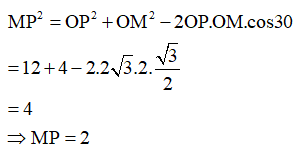
Áp dụng định lí Cosin trong có:
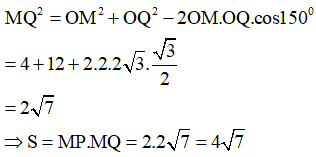
Câu 8:
Cho hai số phức thỏa mãn và .
Tìm giá trị lớn nhất m của biểu thức .
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp : Đặt ![]()
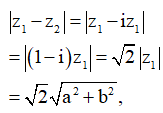
tìm GTLN của ![]()
Cách giải : Đặt ![]()
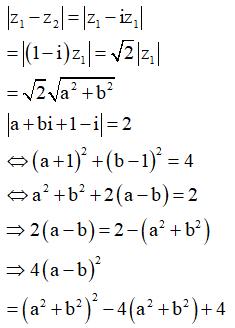
Ta có :
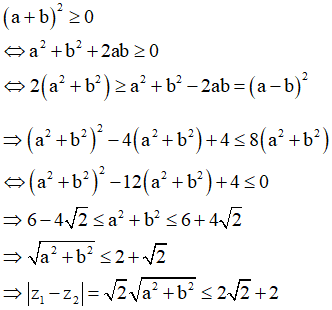
Câu 9:
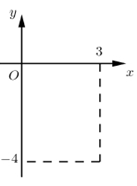
Điểm M trong hình bên là điểm biểu diễn của số phức z. Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án A.
Phương pháp : Số phức z=a+bi có điểm biểu diễn trên mặt phẳng phức là M(a;b) trong đó a là phần thực và b là phần ảo.
Cách giải: M(3;-4)
Số phức z có phần thực là 3 và phần ảo là -4.
Câu 10:
Kí hiệu là hai nghiệm phức của phương trình
Giá trị của biểu thức P= bằng:
 Xem đáp án
Xem đáp án
Đáp án C.
Phương pháp: Sử dụng định lí Vi-et.
Cách giải: là hai nghiệm phức của phương trình nên theo định lí Vi-et ta có:
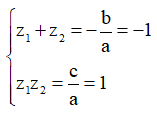
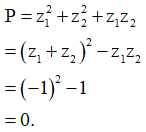
Câu 11:
Xét số phức z thỏa mãn . Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án D.
Phương pháp: Chuyển vế, lấy mođun hai vế.
Cách giải:
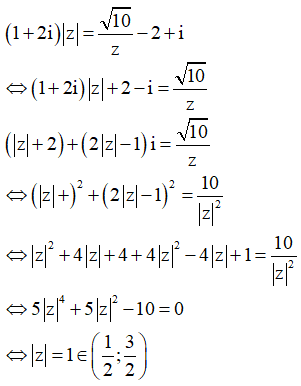
Câu 12:
Xét các số phức thỏa mãn đồng thời hai điều kiện và đạt giá trị nhỏ nhất. Giá trị P=a+2b là:
 Xem đáp án
Xem đáp án
Đáp án A.
Phương pháp:
Từ ![]() tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z=x+yi
tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z=x+yi
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
![]() nhỏ nhất
nhỏ nhất
![]()
Cách giải: Gọi z=x+ui ta có:
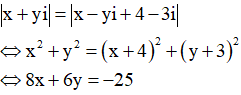
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
![]() nhỏ nhất.
nhỏ nhất.
Ta có: ![]()
Dấu bằng xảy ra ![]()
![]() M thuộc trung trực của AB.
M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có ![]()
Phương trình đường trung trực của AB là
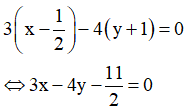
Để ![]()
![]() Tọa độ điểm M là nghiệm của hệ phương trình
Tọa độ điểm M là nghiệm của hệ phương trình
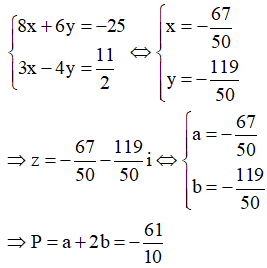
Câu 13:
Tìm phần thực của số phức biết rằng là hai nghiệm phức của phương trình
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp giải: Áp dụng định lí Vi-et của phương trình bậc hai.
Lời giải: Ta có

Câu 14:
Cho số phức . Tìm số phức
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp giải: Bấm máy hoặc khai triển bằng tay tìm số phức w
Lời giải:
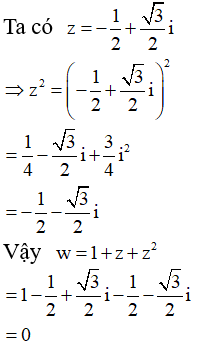
Câu 16:
Biết phương trình có một nghiệm là z=-2+i. Tính a+b
 Xem đáp án
Xem đáp án
Đáp án A
Suy ra được nghiệm còn lại là
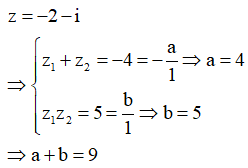
Câu 17:
Với hai số phức và thỏa mãn và , tìm giá trị lớn nhất .
 Xem đáp án
Xem đáp án
Đáp án B
Bổ đề. Cho hai số phức và , ta luôn có
![]() (*)
(*)
Chứng minh. Sử dụng công thức ![]() và
và ![]() .
.
Khi đó
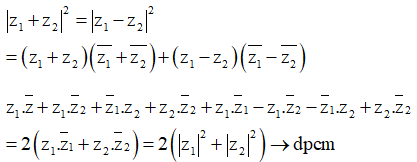
Áp dụng (*), ta được
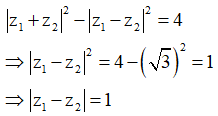
Theo bất đằng thức Bunhiacopxki, ta được
![]()
Câu 18:
Số phức liên hợp của số phức z=2-3i là
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp: Số phức liên hợp của số phức z=a+bi,a,bR là =a-bi
Cách giải: Số phức liên hợp của số phức z=2-3i là =2+3i
Câu 19:
Gọi và là hai nghiệm phức của phương trình .
Giá trị của biểu thức bằng
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp: Giải phương trình phức bậc hai, suy ra các nghiệm và tính tổng bình phương môđun của các nghiệm đó.
Sử dụng công thức: ![]()
Cách giải:
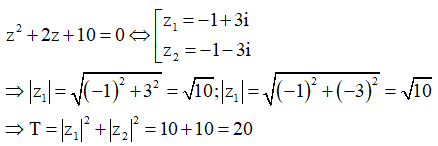
Câu 20:
Xét các số phức thỏa mãn .
Tính P=3a+b khi biểu thức đạt giá trị nhỏ nhất.
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Cách giải:
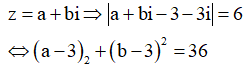
Khi đó ta có:
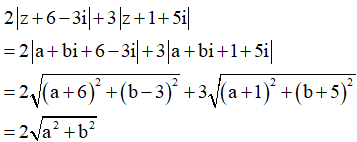
Câu 21:
Số phức z=-4+3i được biểu diễn bởi điểm M có tọa độ
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Điểm biểu diễn của số phức ![]() là M(a;b)
là M(a;b)
Cách giải:
Số phức z=-4+3i được biểu diễn bởi điểm M có tọa độ M(-4;3)
Câu 22:
Gọi là hai nghiệm của phương trình . Khi đó P=bằng
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Áp dụng định lí Vi –et, xác định tổng và tích hai nghiệm của phương trình bậc hai một ẩn ![]()
Cách giải:
Xét phương trình . Áp dụng định lý Vi-ét:
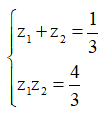
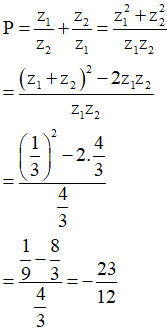
Câu 23:
Cho số phức z thỏa mãn điều kiện .
Giá trị lớn nhất của là
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
- Biểu diễn số phức và giải bài toán tìm GTLN trên mặt phẳng tọa độ.
Cách giải: Gọi I(1;1), J(-1;-3), A(2;3).
Xét số phức ![]() , có điểm biểu diễn là M(x;y)
, có điểm biểu diễn là M(x;y)

![]() M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
Tìm giá trị lớn nhất của ![]() tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
Ta có:
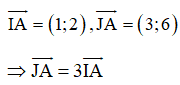
điểm A nằm trên trục lớn của elip.
![]() AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
Gọi S là trung điểm của IJ
![]() S(0;-1)
S(0;-1)
Độ dài đoạn AB=SA+SB
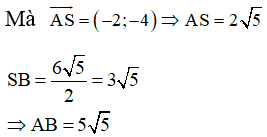
Vậy ![]()
Câu 24:
Có bao nhiêu số phức z thỏa mãn ?
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
+) Đặt ![]()
![]() , thay vào phương trình.
, thay vào phương trình.
+) So sánh hai số phức ![]()
Cách giải: Đặt ![]()
![]() , khi đó ta có:
, khi đó ta có:
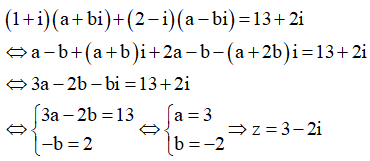
Câu 25:
Trong các số phức z thỏa mãn , gọi và lần lượt là các số phức có môđun lớn nhất và nhỏ nhất.
Khi đó môđun lớn nhất của số phức là:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp : Sử dụng công thức ![]()
Cách giải :
Ta có
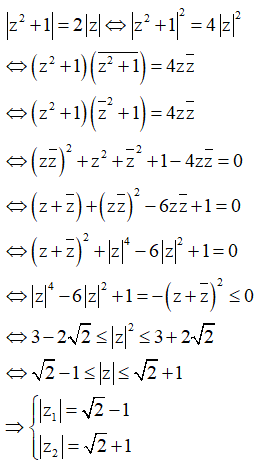
Dấu = xảy ra