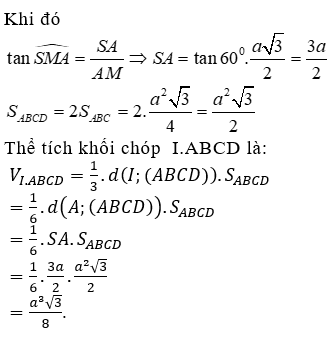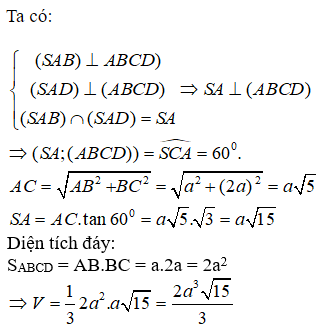Đề kiểm tra 45 phút Toán 12 Chương 1 Hình học có đáp án (Đề 1)
-
1526 lượt thi
-
14 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
I. Trắc nghiệm ( 5 điểm)
Trong các khẳng định sau, khẳng định nào sai?
Xem đáp án
Chọn C.
+ Trong không gian ba chiều, có đúng 5 khối đa diện đều lồi, chúng là các khối đa diện duy nhất có tất cả các mặt, các cạnh và các góc ở đỉnh bằng nhau.
Tứ diện đều | Khối lập phương | Khối bát diện đều | Khối mười hai mặt đều | Khối hai mươi mặt đều |
=> A đúng
+ Hình chóp tam giác đều là hình tứ diện đều → D đúng
+ Hình hộp chữ nhật có diện tích các mặt bằng nhau là khối lập phương → B đúng
+ Trọng tâm các mặt của hình tứ diện đều không thể là các đỉnh của một hình tứ diện đều → C sai.
Câu 3:
Hình chóp tứ giác đều có mấy mặt phẳng đối xứng
Xem đáp án
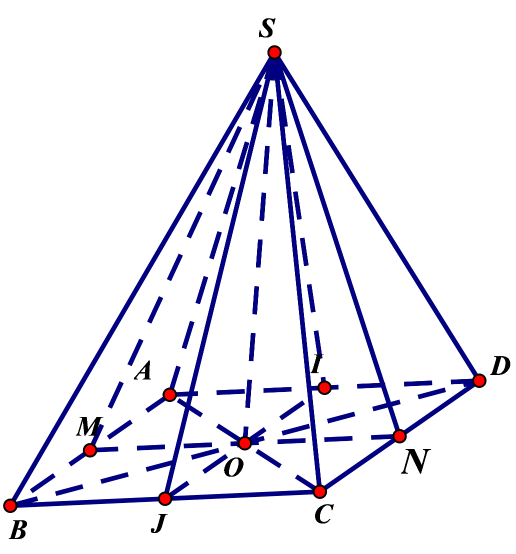
Hình chóp tứ giác đều có 4 mặt phẳng đối xứng đó là:
(SAC), (SBD), (SMN), (SIJ), với M, N, I, J lần lượt là trung điểm của AB, CD, DA, BC.
Chọn D.
Câu 4:
Vật thể nào trong các vật thể sau không phải là khối đa diện.
Xem đáp án
Chọn C.
Hình đa diện phải thỏa mãn 2 điều kiện:
+) Hai đa giác bất kì hoặc không có điểm chung, hoặc có 1 đỉnh chung hoặc có 1 cạnh chung.
+) Mỗi cạnh của một đa giác là cạnh chung của đúng 2 đa giác.
Hình C không thỏa mãn điều kiện thứ 2.
Câu 5:
Số đỉnh của một hình bát diện đều là ?
Xem đáp án
Chọn C.
Hình đa diện phải thỏa mãn 2 điều kiện:
+) Hai đa giác bất kì hoặc không có điểm chung, hoặc có 1 đỉnh chung hoặc có 1 cạnh chung.
+) Mỗi cạnh của một đa giác là cạnh chung của đúng 2 đa giác.
Hình C không thỏa mãn điều kiện thứ 2.
Câu 6:
Hình lập phương có mấy mặt phẳng đối xứng ?
Xem đáp án
Chọn D.
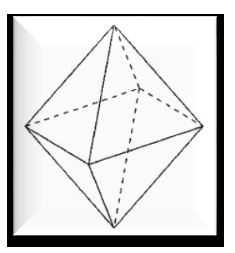
+ Hình bát diện đều là hình có dạng như hình trên:
+ Nên số đỉnh của nó là sáu
Câu 7:
Trong các khối đa diện dưới đây, khối nào có số cạnh có thể là một số lẻ?
Xem đáp án
Chọn D.
* Khối chóp n- giác có tổng số cạnh bằng 2n
* Khối tứ diện có 6 cạnh
* Khối hộp có 12 cạnh
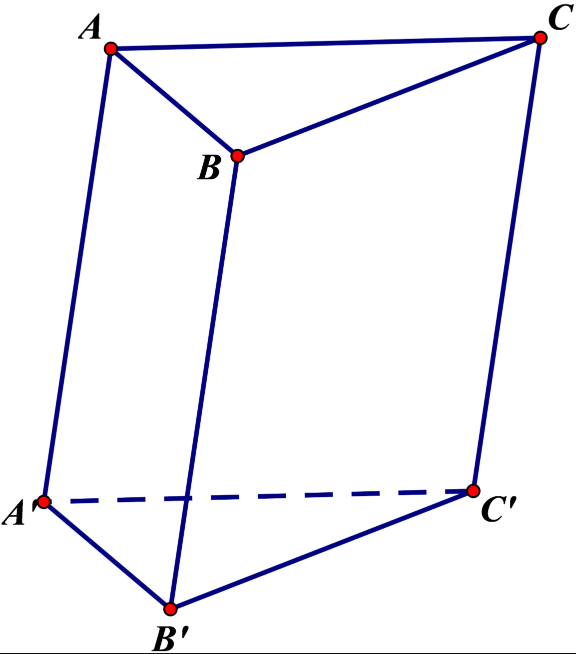
* Khối lăng trụ n-giác với n là một số lẻ thì số cạnh là 3n, là một số lẻ.
Ví dụ: xét lăng trụ tam giác ABC.A'B'C' có 9 cạnh là một số lẻ.
Câu 8:
Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài đường cao không đổi thì thể tích S.ABC tăng lên bao nhiêu lần?
Xem đáp án
Chọn A.
Thể tích hình chóp: 
Khi độ dài cạnh đáy tăng lên 2 lần thì diện tích đáy tăng lên 4 lần.
⇒ Thể tích khối chóp tăng lên 4 lần.
Câu 9:
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật. Tính thể tích S.ABCD biết
Xem đáp án
Chọn C.
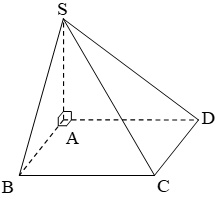
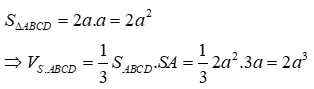
Câu 10:
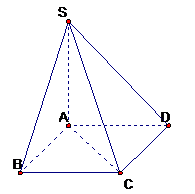
Cho hình chóp S.ABCD đáy hình chữ nhật, SA vuông góc đáy, Góc giữa SB và đáy bằng 45°. Thể tích khối chóp là
Xem đáp án
Chọn B.
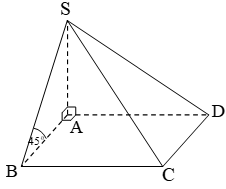
Vì SA vuông góc đáy và góc giữa SB và đáy bằng 45° nên
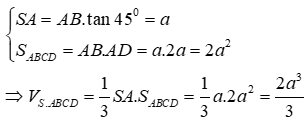
Câu 11:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Tính thể tích khối chóp S.ABC biết
Xem đáp án
Chọn C.
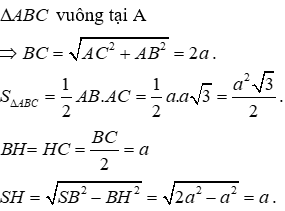
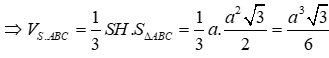
Câu 12:
II. Tự luận ( 5 điểm)
Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau:
BA = 3a, BC = BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM
Xem đáp án
Khối chóp C.BDNM có CB là đường cao nên có thể tích 
trong đó
+ BC = 2a
+ Tứ giác BDNM là hình thang vuông tại B, M do MN là đường trung bình của tam giác ABD nên
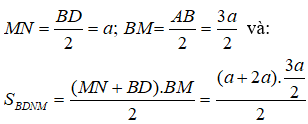
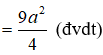
Thể tích của khối chóp C.BDNM là:
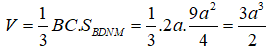
Câu 13:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, , SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng
Xem đáp án
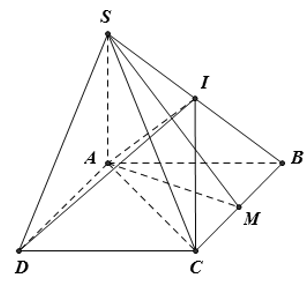
* Ta có SA ⊥ (ABCD) nên AM là hình chiếu của SM trên mặt phẳng (ABCD)
* ΔABCcó AB = BC = a ( vì ABCD là hình thoi) và 
nên ΔABC đều.
