Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 7)
-
2058 lượt thi
-
53 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Một mảnh đất hình chữ nhật có chu vi 96 m, chiều dài bằng chiều rộng. Người ta đã sử dụng diện tích mảnh đất để xây nhà. Tính diện tích phần đất xây nhà.
 Xem đáp án
Xem đáp án
Nửa chu vi của mảnh đất là: 96 : 2 = 48 (m).
Tổng số phần bằng nhau là: 5 + 3 = 8 (phần)
Chiều dài của mảnh đất là: 48 : 8 . 5 = 30 (m).
Chiều rộng của mảnh đất là: 48 – 30 = 18 (m).
Diện tích mảnh đất là: 30 . 18 = 540 (m2).
Diện tích phần đất xây nhà là: (m2).
Đáp số: 45 m2.
Câu 2:
Một sân vườn hình chữ nhật có chu vi là 64 m, chiều dài gấp 3 lần chiều rộng.
a) Tính diện tích khu vườn.
 Xem đáp án
Xem đáp án
a) Nửa chu vi sân vườn là: 64 : 2 = 32 (m).
Chiều dài của sân vườn là: 32 : (3 + 1) . 3 = 24 (m).
Chiều rộng của sân vườn là: 32 – 24 = 8 (m).
Diện tích khu vườn là: 24 . 8 = 192 (m2).
Câu 3:
b) Người ta dự định rào khu vườn bằng lưới kẽm. Biết mỗi mét lưới kẽm giá 100 000 đồng. Tính số tiền mua lưới.
 Xem đáp án
Xem đáp án
b) Số tiền mua lưới kẽm là: 64 . 100 000 = 6 400 000 (đồng).
Đáp số: a) 192 m2;
b) 6 400 000 đồng.
Câu 4:
 Xem đáp án
Xem đáp án
Đổi: 25 ha = 250 000 m2.
Diện tích vườn hoa chiếm số phần diện tích công viên là: .
Đáp số: .
Câu 5:
Một đơn vị chuẩn bị đủ gạo cho 750 người ăn trong 40 ngày. Nhưng có thêm một số người đến nên chỉ ăn trong 25 ngày là hết gạo. Hỏi số người chuyển đến là bao nhiêu? (Mức ăn mỗi người là như nhau).
 Xem đáp án
Xem đáp án
Tóm tắt: 750 người: 40 ngày.
? người: 25 ngày.
Bài giải
Số người ăn hết số gạo trong 1 ngày là:
750 . 40 = 30 000 (người).
Số người ăn hết gạo đơn vị đã chuẩn bị trong 25 ngày là:
30 000 : 25 = 1 200 (người).
Số người chuyển đến thêm là:
1 200 – 750 = 450 (người).
Đáp số: 450 người.
Câu 6:
Một đội công nhân có 8 người sửa xong một đoạn đường trong 12 ngày. Biết mức làm của mỗi người như nhau. Hỏi:
a) Nếu đội công nhân có 12 người thì sửa xong đoạn đường trong bao nhiêu ngày?
 Xem đáp án
Xem đáp án
a) Số ngày 1 công nhân sửa xong đoạn đường là:
12 . 8 = 96 (ngày).
Nếu đội công nhân có 12 người thì sửa xong đoạn đường trong số ngày là:
96 : 12 = 8 (ngày).
Câu 7:
b) Muốn sửa xong đoạn đường trong 6 ngày thì cần bao nhiêu công nhân?
 Xem đáp án
Xem đáp án
b) Muốn sửa xong đoạn đường trong 6 ngày thì cần số công nhân là:
96 : 6 = 16 (công nhân).
Đáp số: a) 8 ngày;
b) 16 công nhân.
Câu 8:
Thực hiện phép tính: (715.40 + 715.9) : 717.
 Xem đáp án
Xem đáp án
Lời giải
(715.40 + 715.9) : 717
= (40 + 9) . 715 : 717
= 49 . 715 : 717
= 72 . 715 : 717
= 72 + 15 : 717
= 717 : 717
= 717 – 17
= 70
= 1.
Câu 9:
Nhân dịp lễ 20/10, shop thời trang Gumac giảm giá 40% cho các mặt hàng. Lan mua cái đầm hết 297 000 đồng. Tính giá tiền cái đầm trước khi giảm.
 Xem đáp án
Xem đáp án
Giá tiền cái đầm trước khi giảm giá là:
297 000 : (100% – 40%) = 495 000 (đồng).
Đáp số: 495 000 đồng.
Câu 10:
Năm nay Lan 12 tuổi, tuổi bà gấp 7 lần tuổi Lan. Hỏi năm nay bà bao nhiêu tuổi? Hỏi Lan sinh vào năm nào và năm đó thuộc thế kỉ nào?
 Xem đáp án
Xem đáp án
Số tuổi của bà là: 12 . 7 = 84 (tuổi).
Lan sinh vào năm: 2023 – 12 = 2011.
Năm 2011 thuộc thế kỉ thứ 21Câu 11:
Năm nay Lan được 12 tuổi. Còn mẹ của Lan thì được 32 tuổi. Hỏi sau 8 năm nữa thì số tuổi của mẹ gấp mấy lần số tuổi của Lan?
 Xem đáp án
Xem đáp án
Số tuổi của mẹ sau 8 năm nữa là:
32 + 8 = 40 (tuổi).
Số tuổi của Lan sau 8 năm nữa là:
12 + 8 = 20 (tuổi).
Sau 8 năm nữa thì số tuổi của mẹ gấp số lần số tuổi của Lan là:
40 : 20 = 2 (lần).
Đáp số: 2 lần.
Câu 12:
Số bi của An bằng số bi của Bình. Nếu Bình có thêm 30 viên bi thì số bi của An bằng số bi của Bình. Tính số viên bi ban đầu của mỗi bạn.
 Xem đáp án
Xem đáp án
Giá trị của 1 phần bằng nhau lúc ban đầu là:
30 : 3 = 10 (viên bi).
Số viên bi ban đầu của An là:
10 . 6 = 60 (viên bi).
Số viên bi ban đầu của Bình là:
10 . 5 = 50 (viên bi).
Đáp số: An: 60 viên bi; Bình: 50 viên bi.
Câu 13:
Trong một tháng nào đó có 3 ngày thứ 5 trùng vào ngày chẵn. Hỏi ngày 26 tháng đó là ngày thứ mấy trong tuần?
 Xem đáp án
Xem đáp án
Ta có:
⦁ Thứ năm đầu tiên là ngày 2.
⦁ Thứ năm thứ hai là ngày 9.
⦁ Thứ năm thứ ba là ngày 16.
⦁ Thứ năm thứ tư là ngày 23.
⦁ Thứ năm thứ năm là ngày 30.
Ta không thể chọn thứ năm đầu tiên là ngày 1 hoặc ngày 3 vì trong tháng đó có 3 ngày thứ 5 trùng vào ngày chẵn.
Vậy ngày 26 của tháng đó là ngày Chủ nhật.
Câu 14:
 Xem đáp án
Xem đáp án
Số điểm 10 tổ 1 đạt được là:
(số điểm 10).
Vì tổ 2 đạt số điểm 10 của 2 tổ kia nên tổ 2 đạt số điểm 10 của cả 3 tổ.
Số điểm 10 tổ 2 đạt được là:
(số điểm 10).
Số điểm 10 tổ 3 đạt được là:
120 – 40 – 48 = 32 (số điểm 10).
Đáp số: Tổ 1: 40 số điểm 10.
Tổ 2: 48 số điểm 10.
Tổ 3: 32 số điểm 10.
Câu 15:
 Xem đáp án
Xem đáp án
Điều kiện: x ∈ ℕ*.
Nhà toán học De Morgan sinh năm 1806 nên số tuổi của ông vào năm x2 là x2 – 1806.
Hay x = x2 – 1806.
⇒ x2 – x – 1806 = 0.
⇒ x2 – 43x + 42x – 1806 = 0.
⇒ x(x – 43) + 42(x – 43) = 0.
⇒ (x + 42)(x – 43) = 0.
⇒ x – 43 = 0 hoặc x + 42 = 0.
⇒ x = 43 hoặc x = –42.
So với điều kiện x ∈ ℕ*, ta nhận x = 43.
Vậy vào năm x2 đó, nhà toán học De Morgan 43 tuổi.
Câu 16:
Xe thứ 1 chở 54 tạ thóc, xe 2 chở 66 tạ, xe 3 chở 72 tạ, xe thứ 4 chở được ít hơn trung bình cộng số thóc cả 4 xe đã cho là 9 tạ thóc. Hỏi xe thứ 4 chở được bao nhiêu tạ thóc?
 Xem đáp án
Xem đáp án
3 lần trung bình cộng số tạ thóc cả 4 xe chở được là:
54 + 66 + 72 – 9 = 183 (tạ thóc).
Trung bình cộng số tạ thóc cả 4 xe chở được là:
183 : 3 = 61 (tạ thóc).
Số tạ thóc xe thứ 4 chở được là:
61 – 9 = 52 (tạ thóc).
Đáp số: 52 tạ thóc.
Câu 17:
Giải phương trình |x| + |3 – x| = 6.
 Xem đáp án
Xem đáp án
Ta có |x| + |3 – x| = 6 (1)
Bảng xét dấu:
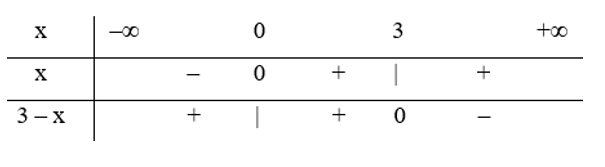
Trường hợp 1: x < 0
Khi đó |x| = –x; |3 – x| = 3 – x
Phương trình (1) tương đương với: –x + 3 – x = 6.
⇔ –2x = 3.
.
So với điều kiện x < 0, ta nhận .
Trường hợp 2: 0 ≤ x ≤ 3
Khi đó |x| = x; |3 – x| = 3 – x
Phương trình (1) tương đương với: x + 3 – x = 0.
⇔ 0x = –3 (vô lí).
Trường hợp 3: x > 3.
Khi đó |x| = x; |3 – x| = –(3 – x)
Phương trình (1) tương đương với: x – 3 + x = 6.
⇔ 2x = 9.
.
So với điều kiện x > 3, ta nhận .
Vậy tập nghiệm của phương trình đã cho là .
Câu 18:
Giải phương trình 3x2(x – 1) + x – 1 = 0.
 Xem đáp án
Xem đáp án
Lời giải
Ta có 3x2(x – 1) + x – 1 = 0.
⇔ (x – 1)(3x2 + 1) = 0.
⇔ x – 1 = 0 hoặc 3x2 + 1 = 0 (vô nghiệm vì 3x2 + 1 > 0).
⇔ x = 1.
Vậy phương trình đã cho có nghiệm là x = 1.
Câu 19:
Cho nửa đường tròn tâm O, đường kính BC và một điểm A trên nửa đường tròn (A khác B và C). Kẻ AH vuông góc với BC (H thuộc BC). Trên nửa mặt phẳng bờ BC chứa A dựng hai nửa đường tròn đường kính HB và HC, chúng lần lượt cắt AB và AC tại E và F.
a) Chứng minh rằng AE.AB = AF.AC.
 Xem đáp án
Xem đáp án
a)

Gọi P, Q lần lượt là tâm của hai nửa đường tròn đường kính HB và HC.
Ta có:
⦁ (góc nội tiếp chắn nửa đường tròn đường kính HB).
⦁ (góc nội tiếp chắn nửa đường tròn đường kính HC).
Tam giác ABH vuông tại H có HE là đường cao:
AH2 = AE.AB (hệ thức lượng trong tam giác vuông) (1)
Tam giác ACH vuông tại H có HF là đường cao:
AH2 = AF.AC (hệ thức lượng trong tam giác vuông) (2)
Từ (1), (2), ta thu được AE.AB = AF.AC.
Câu 20:
b) Chứng minh rằng EF là tiếp tuyến chung của hai nửa đường tròn đường kính HB và HC.
 Xem đáp án
Xem đáp án
b) Ta có (góc nội tiếp chắn nửa đường tròn (O)).
Tứ giác AEHF, có: .
Suy ra tứ giác AEHF là hình chữ nhật.
Gọi D là giao điểm của hai đường chéo AH và EF.
Suy ra DA = DH = DE = DF.
Xét ∆PED và ∆PHD, có:
PE = PH (bằng bán kính của nửa đường tròn đường kính HB);
DE = DH (chứng minh trên);
PD chung.
Do đó ∆PED = ∆PHD (c.c.c).
Suy ra (do AH ⊥ BC).
Vì vậy EF là tiếp tuyến của nửa đường tròn đường kính HB.
Chứng minh tương tự, ta được EF là tiếp tuyến của nửa đường tròn đường kính HC.
Vậy EF là tiếp tuyến chung của hai nửa đường tròn đường kính HB và HC.
Câu 21:
c) Gọi I và K lần lượt là hai điểm đối xứng với H qua AB và AC. Chứng minh rằng ba điểm I, A, K thẳng hàng.
 Xem đáp án
Xem đáp án
c) Ta có AB là đường trung trực của đoạn HI (do I là điểm đối xứng với H qua AB).
Suy ra AH = AI.
Do đó tam giác AHI cân tại A.
Vì vậy AB vừa là đường trung trực, vừa là đường phân giác của tam giác AHI.
Suy ra .
Chứng minh tương tự, ta được .
Ta có .
.
Vậy ba điểm I, A, K thẳng hàng.
Câu 22:
d) Đường thẳng IK cắt tiếp tuyến kẻ từ B của nửa đường tròn (O) tại M. Chứng minh rằng MC, AH và EF đồng quy.
 Xem đáp án
Xem đáp án
d) Ta có ∆OAC cân tại O (OA = OC = R).
Suy ra (3)
Lại có ∆ABC vuông tại A. Suy ra (4)
Ta có ∆ABH vuông tại H. Suy ra (5)
Từ (3), (4), (5), suy ra .
Mà (chứng minh trên).
Do đó .
Mà .
Suy ra .
Do đó .
Vì vậy IA là tiếp tuyến của (O).
Mà BM cũng là tiếp tuyến của (O) (giả thiết).
Suy ra AM = BM (tính chất hai tiếp tuyến cắt nhau).
Gọi N là giao điểm của AC và BM.
Ta có BM ⊥ BH (do BM là tiếp tuyến của nửa đường tròn (O)) và AH ⊥ BC (giả thiết).
Suy ra BM // AH.
Mà M là trung điểm BN (tam giác ABN vuông tại A có AM = BM).
Do đó CM đi qua trung điểm D của AH (do D là giao điểm của hai AH và EF trong hình chữ nhật AEHF).
Vậy ba đường thẳng MC, AH và EF đồng quy.
Câu 23:
Tìm một số tự nhiên có 2 chữ số, biết rằng nếu viết thêm một chữ số 0 vào giữa chữ số hàng chục và hàng đơn vị thì ta được số mới gấp 7 lần số cũ.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là (a, b ∈ ℕ, 0 < a ≤ 9, 0 ≤ b ≤ 9).
Nếu viết thêm một chữ số 0 vào giữa chữ số hàng chục và hàng đơn vị thì ta được số mới gấp 7 lần số cũ.
Suy ra số mới là và .
Ta có .
⇒ 100a + b = 7(10a + b).
⇒ 100a + b = 70a + 7b.
⇒ 30a = 6b.
⇒ 5a = b.
Với a = 1, ta có: b = 5 (nhận).
Với a = 2, ta có: b = 10 (loại).
Vậy số cần tìm là 15.
Câu 24:
Cho . Tìm a sao cho x là số dương.
 Xem đáp án
Xem đáp án
Ta có x là số dương hay x > 0.
.
⇔ 7 – a > 0.
⇔ a < 7.
Vậy a < 7 thì x là số dương.
Câu 25:
Một kho gạo có 60 tấn gạo tẻ và gạo nếp, trong đó số gạo nếp bằng số gạo tẻ. Tính số gạo nếp, gạo tẻ có trong kho?
 Xem đáp án
Xem đáp án
Tổng số phần bằng nhau là:
3 + 7 = 10 (phần).
Giá trị của 1 phần là:
60 : 10 = 6 (tấn gạo).
Số tấn gạo nếp có trong kho là:
3 . 6 = 18 (tấn gạo).
Số tấn gạo tẻ có trong kho là:
7 . 6 = 42 (tấn gạo).
Đáp số: 18 tấn gạo nếp; 42 tấn gạo tẻ.
Câu 26:
Một người đi xe đạp với vận tốc v1 = 18 km/h và một người đi bộ với vận tốc v2 = 4 km/h khởi hành cùng một lúc ở cùng một nơi và chuyển động ngược chiều nhau. Sau khi đi được 30 phút, người đi xe đạp dừng lại nghỉ 30 phút rồi quay lại đuổi theo người đi bộ với vận tốc như cũ. Hỏi kể từ lúc khởi hành, sau bao lâu người đi xe đạp đuổi kịp người đi bộ.
 Xem đáp án
Xem đáp án
Đổi: 30 phút = 0,5 h.
Quãng đường người đi xe đạp đi trong 30 phút là:
s1 = v1.t1 = 18.0,5 = 9 (km).
Quãng đường người đi bộ đi trong 1 h là:
s2 = v2.t2 = 4.1 = 4 (km).
Thời gian để người đi xe đạp đuổi kịp người đi bộ là:
(h).
Vậy thời gian kể từ khi khởi hành đến khi người đi xe đạp đuổi kịp người đi bộ là:
(h) ≈ 1 h 55’Câu 27:
Số 49 200 000 đọc thế nào?
 Xem đáp án
Xem đáp án
Số 49 200 000 đọc là: bốn mươi chín triệu hai trăm nghìn.
Câu 28:
 Xem đáp án
Xem đáp án
Điều kiện: x ≠ 0.
Ta có
hoặc .
Vậy tập nghiệm của hệ phương trình đã cho là: S = {(150; 50); (75; –25)}.
Câu 29:
Tìm x ∈ ℕ, biết 8x + 30 chia hết cho 2x + 3.
 Xem đáp án
Xem đáp án
Ta có 8x + 30 = 4(2x + 3) + 18.
Ta có 4(2x + 3) ⋮ (2x + 3).
Suy ra 8x + 30 ⋮ (2x + 3) khi 18 ⋮ (2x + 3).
Với x ∈ ℕ thì 2x + 3 ≥ 3 và 2x + 3 là số lẻ nên 2x + 3 ∈ {3; 9}.
Ta có bảng sau:
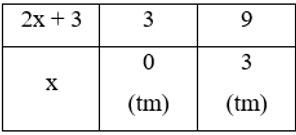
Vậy x ∈ {0; 3} thỏa mãn yêu cầu bài toán.
Câu 30:
Cho đường tròn tâm O có ba điểm A, B, C nằm trên đường tròn, trong đó BC là dây cung lớn nhất, AB là dây cung có độ dài bằng .
a) Vẽ các dây cung AB, BC.
 Xem đáp án
Xem đáp án
a)
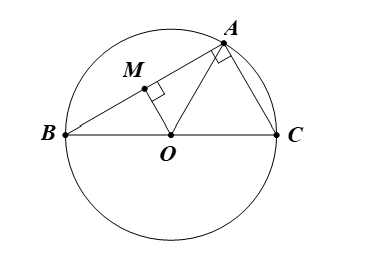
Câu 31:
b) Tính độ dài dây AC.
 Xem đáp án
Xem đáp án
b) Vì BC là dây cung lớn nhất nên AB là đường kính của đường tròn (O).
Suy ra O là trung điểm của BC.
Gọi M là trung điểm của AB.
Suy ra OM ⊥ AB (quan hệ giữa đường kính và dây cung) và .
Tam giác AMO vuông tại M: OM2 = AO2 – AM2 (Định lí Pytago).
.
Suy ra .
Tam giác ABC có O, M lần lượt là trung điểm của BC, AB.
Suy ra OM là đường trung bình của tam giác ABC.
Vậy AC = 2OM = R.
Câu 32:
c) Tính các góc của tam giác ABC.
 Xem đáp án
Xem đáp án
c) Ta có là góc nội tiếp chắn nửa đường tròn.
Suy ra .
Tam giác ABC vuông tại A: .
Suy ra .
Tam giác ABC, có: .
Vậy ; và .
Câu 33:
Một chiếc bánh được chia làm 18 miếng. Mai đã ăn hết chiếc bánh, Chi đã ăn hết chiếc bánh, Hải đã ăn hết chiếc bánh và Minh đã ăn nốt số bánh còn lại. Hỏi Minh đã ăn bao nhiêu miếng bánh?
 Xem đáp án
Xem đáp án
Lời giải
Số miếng bánh Mai đã ăn hết là:
(miếng bánh).
Số miếng bánh Chi đã ăn hết là:
(miếng bánh).
Số miếng bánh Hải đã ăn hết là:
(miếng bánh).
Số miếng bánh Minh đã ăn hết là:
18 – 6 – 3 – 2 = 7 (miếng bánh).
Đáp số: 7 miếng bánh.
Câu 34:
Cho dãy số tự nhiên cách đều gồm 11 số hạng có tổng bằng 176, biết rằng hiệu của số hạng cuối cùng và số hạng đầu tiên bằng 30. Hãy viết dãy số đó.
 Xem đáp án
Xem đáp án
Khoảng cách giữa hai số hạng là: 30 : (11 – 1) = 3 (đơn vị).
Tổng của số hạng cuối cùng và số hạng đầu tiên là: 176 ⨯ 2 : 11 = 32.
Số hạng đầu tiên là: (32 – 30) : 2 = 1.
Số hạng cuối cùng là: (32 + 30) : 2 = 31.
Vậy dãy số cần tìm là: 1; 4; 7; 10; 13; 16; 19; 22; 25; 28; 31.
Câu 35:
Cho a + b + c = 0 và a, b, c ≠ 0. Tính giá trị của biểu thức:
. Xem đáp án
Xem đáp án
Ta có a + b + c = 0. Suy ra .
Với b + c = –a, ta có b2 + c2 + 2bc = a2.
Suy ra b2 + c2 = a2 – 2bc.
Chứng minh tương tự, ta được: a2 + b2 = c2 – 2ab và a2 + c2 = b2 – 2ac.
Khi đó
.
Vậy .
Câu 36:
Cho dãy số tự nhiên gồm 10 số hạng có tổng bằng 3400. Biết mỗi số hơn số liền trước 10 đơn vị. Tìm số hạng đầu tiên và số hạng cuối cùng của dãy.
 Xem đáp án
Xem đáp án
Tổng của số hạng đầu tiên và số hạng cuối cùng là:
3400 ⨯ 2 : 10 = 680.
Hiệu của số hạng đầu tiên và số hạng cuối cùng là:
(10 – 1) ⨯ 10 = 90.
Số hạng đầu tiên là:
(680 – 90) : 2 = 295.
Số hạng cuối cùng là:
(680 + 90) : 2 = 385.
Đáp số: Số hạng đầu tiên: 295;
Số hạng cuối cùng: 385.
Câu 37:
Tìm các số nguyên tố a, b, c sao cho abc = 3(a + b + c).
 Xem đáp án
Xem đáp án
Ta có a, b, c là số nguyên tố. Suy ra a, b, c cũng là số tự nhiên.
Do đó a + b + c ∈ ℕ.
Vì vậy 3(a + b + c) ⋮ 3.
Suy ra abc ⋮ 3.
Do đó tồn tại ít nhất một trong ba số a, b, c chia hết cho 3.
Trường hợp 1: a = b = c = 3.
Ta có abc = 3(a + b + c).
Suy ra 3.3.3 = 3(3 + 3 + 3) (thỏa mãn).
Trường hợp 2: Tồn tại hai số chia hết cho 3.
Giả sử a, b chia hết cho 3. Tức là, a = b = 3.
Ta có abc = 3(a + b + c).
Suy ra 3.3.c = 3(3 + 3 + c).
Do đó 9c = 18 + 3c.
Vì vậy 6c = 18.
Suy ra c = 3.
Lúc này, ta thấy c = 3 không thỏa mãn điều kiện của trường hợp 2 vì chỉ có hai số chia hết cho 3.
Trường hợp 3: Nếu chỉ tồn tại một số chia hết cho 3.
Giả sử a chia hết cho 3. Tức là, a = 3.
Ta có abc = 3(a + b + c).
Suy ra 3bc = 9 + 3b + 3c.
Do đó bc = 3 + b + c.
Vì vậy bc – b – c + 1 = 4.
Suy ra b(c – 1) – (c – 1) = 4.
Do đó (b – 1)(c – 1) = 4 (*)
Vì b, c là số nguyên tố nên b – 1; c – 1 là số tự nhiên.
Vì vậy b – 1 ∈ Ư(4) = {1; 2; 4}.
Suy ra b ∈ {2; 3; 5}.
So với điều kiện của trường hợp 3, ta nhận b ∈ {2; 5}.
Thay b = 2 vào (*), ta được: c – 1 = 4. Suy ra c = 5.
Thay b = 5 vào (*), ta được c – 1 = 1. Suy ra c = 2.
Vậy các bộ số (a; b; c) thỏa mãn yêu cầu bài toán là (3; 3; 3), (3; 2; 5), (3; 5; 2), (2; 3; 5), (2; 5; 3), (5; 3; 2), (5; 2; 3).
Câu 38:
Một tàu hỏa cần chở 872 khách tham quan. Biết rằng mỗi toa có 10 ngăn, mỗi ngăn có 6 chỗ ngồi. Cần ít nhất mấy toa để chở hết số khách tham quan?
 Xem đáp án
Xem đáp án
Số chỗ ngồi của mỗi toa là: 10 . 6 = 60 (chỗ ngồi).
Ta có: 872 : 60 = 14 dư 32.
Suy ra cần thêm 1 toa để chở 32 khách tham quan.
Cần ít nhất số toa để chở hết số khách tham quan là: 14 + 1 = 15 (toa).
Đáp số: 15 toa.
Câu 39:
Chứng tỏ rằng là phân số tối giản (n ∈ ℕ).
 Xem đáp án
Xem đáp án
Để chứng minh là phân số tối giản (n ∈ ℕ), ta cần chứng minh phân số này có tử và mẫu là hai số nguyên tố cùng nhau (ước chung lớn nhất của hai số đó bằng 1).
Gọi d là ước chung của 12n + 1 và 30n + 2 (n ∈ ℕ).
⇒ (60n + 5) – (60n + 4) ⋮ d.
⇒ 1 ⋮ d.
⇒ d = 1.
Do đó 12n + 1 và 30n + 2 là hai số nguyên tố cùng nhau.
Vậy phân số là phân số tối giản (n ∈ ℕ).
Câu 40:
Một ô tô chạy 100 km hết 13 lít xăng. Hỏi cần bao nhiêu xăng khi ô tô chạy quãng đường 300 000 m?
 Xem đáp án
Xem đáp án
Đổi: 300 000 m = 300 km.
300 km gấp 100 km số lần là:
300 : 100 = 3 (lần).
Ô tô đi quãng đường 300 km thì tiêu thụ hết số lít xăng là:
13 ⨯ 3 = 39 (lít xăng).
Vậy đi 300 000 m thì ô tô cần 39 lít xăng.
Câu 41:
 Xem đáp án
Xem đáp án
Lời giải
Ta có A = 4 + 22 + 23 + 24 + ... + 220.
Đặt B = 22 + 23 + 24 + ... + 220.
Suy ra 2B = 23 + 24 + ... + 221.
Ta có 2B – B = (23 + 24 + ... + 221) – (22 + 23 + 24 + ... + 220).
Suy ra B = (23 – 23) + (24 – 24) + ... + (220 – 220) + 221 – 22 = 221 – 22.
Khi đó A = 4 + B = 4 + 221 – 22 = (22 – 22) + 221 = 221.
Vậy A = 221.
Câu 42:
Cho đường tròn tâm O bán kính 2,5 cm và dây AB di động sao cho AB = 4 cm. Hỏi trung điểm H của AB di động trên đường nào?
 Xem đáp án
Xem đáp án
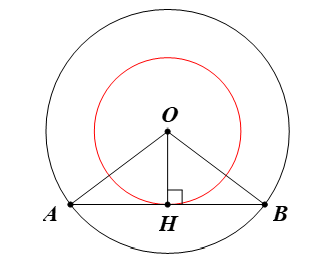
Ta có: OA = OB = R.
Suy ra tam giác OAB cân tại O.
Mà OH là đường trung tuyến của tam giác OAB.
Do đó OH cũng là đường cao của tam giác OAB.
Vì vậy tam giác OAH vuông tại H.
Suy ra (Định lí Pitago).
.
Suy ra OH = 1,5 (cm).
Vậy H di động trên đường tròn tâm O bán kính 1,5 cm.
Câu 43:
Cho đường tròn (O; R). Vẽ hai bán kính OA, OB. Trên các bán kính OA, OB lần lượt lấy các điểm M, N sao cho OM = ON. Vẽ dây CD đi qua M, N (M nằm giữa C và N).
a) Chứng minh CM = DN.
 Xem đáp án
Xem đáp án
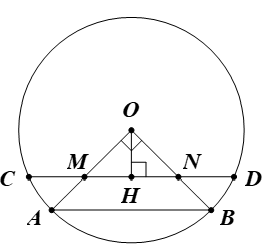
a) Kẻ OH ⊥ CD (H ∈ CD).
Suy ra H là trung điểm CD.
Do đó HC = HD (quan hệ giữa đường kính và dây cung) (1)
Tam giác OMN cân tại O (do OM = ON).
Suy ra OH vừa là đường cao, vừa là đường trung tuyến của tam giác OMN.
Do đó HM = HN (2)
Lại có CH = CM + MH và DH = DN + NH (3)
Từ (1), (2), (3), suy ra CM = DN.
Câu 44:
b) Giả sử . Tính OM theo R sao cho CM = MN = ND.
 Xem đáp án
Xem đáp án
b) Đặt OH = x (x > 0).
Tam giác OMN vuông cân tại O có OH là đường trung tuyến.
Suy ra OH = MH = NH = x.
Do đó HD = HN + ND = HN + MN = HN + 2HN = 3HN = 3x.
Tam giác OMH vuông cân tại H: .
Áp dụng định lí Pitago cho tam giác HOD vuông tại H, ta được:
OH2 + HD2 = OD2.
⇔ x2 + 9x2 = R2.
⇔ 10x2 = R2.
.
Áp dụng định lí Pitago cho tam giác OMH vuông tại H, ta được:
.
Vậy .
Câu 45:
 Xem đáp án
Xem đáp án
Ta có (x – y)2 + (y – z)2 + (z – x)2
= x2 – 2xy + y2 + y2 – 2yz + z2 + z2 – 2zx + x2
= 2x2 + 2y2 + 2z2 – 2xy – 2yz – 2zx
= 2(x2 + y2 + z2 – xy – yz – zx).
Câu 46:
Cho (x – y)2 + (y – z)2 + (z – x)2 = 4(x2 + y2 + z2 – xy – yz – zx). Chứng minh x = y = z.
 Xem đáp án
Xem đáp án
Ta có (x – y)2 + (y – z)2 + (z – x)2 = 4(x2 + y2 + z2 – xy – yz – zx).
⇔ x2 – 2xy + y2 + y2 – 2yz + z2 + z2 – 2zx + x2 = 4(x2 + y2 + z2 – xy – yz – zx).
⇔ 2x2 + 2y2 + 2z2 – 2xy – 2yz – 2zx = 4(x2 + y2 + z2 – xy – yz – zx).
⇔ 2(x2 + y2 + z2 – xy – yz – zx) = 4(x2 + y2 + z2 – xy – yz – zx).
⇔ 2(x2 + y2 + z2 – xy – yz – zx) = 0.
⇔ x2 – 2xy + y2 + y2 – 2yz + z2 + z2 – 2zx + x2 = 0.
⇔ (x – y)2 + (y – z)2 + (z – x)2 = 0.
Vậy ta có điều phải chứng minh.
Câu 47:
Qua đỉnh A của hình vuông ABCD cạnh bằng a, vẽ một đường thẳng cắt BC ở M và cắt DC ở I. Chứng minh .
 Xem đáp án
Xem đáp án
Vẽ Ax ⊥ AI sao cho Ax cắt CD tại J.
Tam giác AIJ vuông tại A có AD là đường cao: (*)
Xét ∆ADJ và ∆ABM, có:
;
AD = AB (ABCD là hình vuông);
(cùng phụ với ).
Do đó ∆ADJ = ∆ABM (g.c.g).
Suy ra AJ = AM (cặp cạnh tương ứng).
Từ (*), suy ra .
Vậy ta có điều phải chứng minh.
Câu 48:
Có bao nhiêu số tự nhiên có 4 chữ số chia hết cho 5?
 Xem đáp án
Xem đáp án
Gọi số có 4 chữ số cần tìm là (a ≠ 0; a, b, c, d < 10 và a, b, c, d ∈ ℕ).
Vì chia hết cho 5 nên d = 0 hoặc d = 5.
Do đó d có 2 cách chọn.
Lại có:
⦁ a có 9 cách chọn (do a ≠ 0).
⦁ b có 10 cách chọn.
⦁ c có 10 cách chọn.
Vậy ta có tất cả 2.9.10.10 = 1800 số tự nhiên thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án C.
Câu 49:
Tìm x, biết: (x – 1) : 0,16 = –9 : (1 – x).
 Xem đáp án
Xem đáp án
Ta có (x – 1) : 0,16 = –9 : (1 – x)
⇒ (x – 1) : 0,16 = –9 : [(–1).(x – 1)]
⇒ (x – 1) : 0,16 = 9 : (x – 1)
⇒ (x – 1)(x – 1) = 9 . 0,16
⇒ (x – 1)2 = 1,44 = 1,22 = (–1,2)2
⇒ x – 1 = 1,2 hoặc x – 1 = –1,2
⇒ x = 1,2 + 1 = 2,2 hoặc x = –1,2 + 1 = –0,2.
Vậy x = 2,2 hoặc x = –0,2.
Câu 50:
a) Tìm hai số tự nhiên liên tiếp có tích bằng 650.
b) Tìm hai số chẵn liên tiếp có tích bằng 1088.
 Xem đáp án
Xem đáp án
a) Ta có 650 = 2 . 25 . 13 = 25 . (2 . 13) = 25 . 26.
Vậy hai số tự nhiên liên tiếp có tích bằng 650 là 25 và 26.
b) Ta có 1088 = 26 . 17 = 25 . (2 . 17) = 32 . 34.
Vậy hai số chẵn liên tiếp có tích bằng 1088 32 và 34.
Câu 51:
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành BH = 2 cm, CH = 8 cm. Giải tam giác vuông này.
 Xem đáp án
Xem đáp án
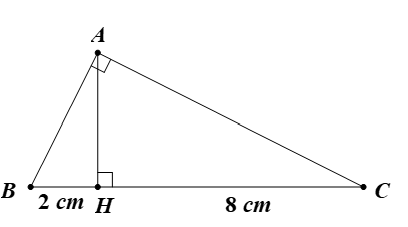
Ta có: BC = BH + CH = 2 + 8 = 10 (cm).
Áp dụng hệ thức lượng cho tam giác ABC vuông tại A có AH là đường cao, ta được:
⦁ AB2 = BH.BC = 2.10 = 20. Suy ra (cm).
⦁ AC2 = CH.BC = 8.10 = 80. Suy ra (cm).
Tam giác ABC vuông tại A:
⦁ . Suy ra .
⦁ .
Vậy BC = 10 cm; cm; cm; và .
Câu 52:
Cho IX = V – I. Hãy đổi chỗ 2 que tính để được phép tính mới bằng 1, rồi viết phép tính đó bằng số La Mã.
 Xem đáp án
Xem đáp án
Câu 53:
Khi lấy tổng các số tự nhiên từ 1 đến 49 cộng với 25 ta được kết quả là
 Xem đáp án
Xem đáp án
Xét tổng 1 + 2 + 3 + ... + 49:
Số các số hạng là: (49 – 1) : 1 + 1 = 49 (số hạng).
Khi đó tổng là: 1 + 2 + 3 + ... + 49 = (49 + 1) ⨯ 49 : 2 = 1225.
Vậy khi lấy tổng các số tự nhiên từ 1 đến 49 cộng với 25, ta được: 1225 + 25 = 1250.
