Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 8)
-
1981 lượt thi
-
52 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Một quyển sách tăng 25% giá thì được giá mới. Hỏi giá mới phải giảm đi bao nhiêu phần trăm để được trở lại giá ban đầu?
 Xem đáp án
Xem đáp án
Giá của quyển sách tăng 25% tức là tăng thêm của nó.
Ta có sơ đồ:
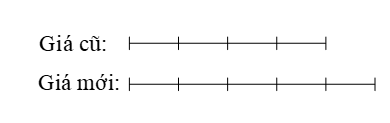
Vậy giá mới phải giảm đi để được trở lại giá ban đầu.
Câu 2:
Năm nay, tổng số tuổi của hai mẹ con là 50 tuổi, tuổi mẹ gấp 4 lần tuổi con. Hỏi 5 năm nữa, mẹ bao nhiêu tuổi? Con bao nhiêu tuổi?
 Xem đáp án
Xem đáp án
Tổng số phần bằng nhau là: 4 + 1 = 5 (phần).
Tuổi của mẹ là: 50 : 5 ⨯ 4 = 40 (tuổi).
Tuổi của con là: 50 : 5 ⨯ 1 = 10 (tuổi).
Đáp số: Tuổi mẹ: 40 tuổi;
Tuổi con: 10 tuổi.Câu 3:
Số học sinh của một trường là một số tự nhiên có 3 chữ số và lớn hơn 900. Mỗi lần xếp hàng 3, hàng 4, hàng 5 đều không có ai lẻ hàng. Tính số học sinh của trường đó?
 Xem đáp án
Xem đáp án
Gọi số học sinh của trường đó là x (900 < x < 1000 và x ∈ ℕ).
Mỗi lần xếp hàng 3, hàng 4, hàng 5 đều không có ai lẻ hàng.
Suy ra x chia hết cho 3, 4, 5 hay x là BC(3, 4, 5).
Mà BCNN(3, 4, 5) = 60.
Do đó x ∈ B(60) = {0; 60; 120; 180; 240; 300; ...}.
Mà 900 < x < 1000 và x ∈ ℕ nên x = 960.
Vậy số học sinh của trường đó là 960.
Câu 4:
 Xem đáp án
Xem đáp án
Công thức tổng quát cho dãy số Fibonacci:
.
Do đó số thứ 100 trong dãy số Fibonacci là:
.
Câu 5:
 Xem đáp án
Xem đáp án
Vì x ⋮ 12, x ⋮ 21 và x ⋮ 28 nên x ∈ BC(12, 21, 28).
Ta có:
⦁ 12 = 22.3;
⦁ 21 = 3.7;
⦁ 28 = 22.7.
Suy ra BCNN(12, 21, 28) = 22.3.7 = 84.
Do đó x ∈ BC(12, 21, 28) = B(84) = {0; 84; 168; 252; 336; 420; 504; ...}.
Mà 150 < x < 300 nên x = 168 hoặc x = 252.
Vậy x = 168 hoặc x = 252 thỏa mãn yêu cầu bài toán.
Câu 6:
 Xem đáp án
Xem đáp án
Đặt B = 23.33.43. ... .253.263.
Số thừa số của tích B là: (263 – 23) : 10 + 1 = 25 (thừa số).
Ta thấy tích của 4 thừa số có tận cùng là 3 thì có tận cùng là 1.
Vì có 25 thừa số nên ta kết hợp được 6 nhóm, mỗi nhóm có 4 thừa số và còn thừa 1 thừa số là 263. Tích của mỗi nhóm trên có chữ số tận cùng là 1. Do đó tích của 6 nhóm trên có tận cùng là 1.
Khi đó tích của nhóm trên với thừa số 263 sẽ có tận cùng là 3.
Vậy hiệu A = B – 9756 có tận cùng là 7.
Câu 7:
 Xem đáp án
Xem đáp án
Vì x chia hết cho 9 nên x ∈ B(9) = {0; 9; 18; 27; 36; 45; ...}.
Mà x < 40 nên x ∈ {0; 9; 18; 27; 36}.
Vậy ∈ {0; 9; 18; 27; 36}.
Câu 8:
Tìm số tự nhiên x, biết: x chia hết cho 4; x chia hết cho 7; x chia hết cho 8 và x nhỏ nhất.
 Xem đáp án
Xem đáp án
Vì x ⋮ 4; x ⋮ 7; x ⋮ 8 và x nhỏ nhất nên x ∈ BCNN(4, 7, 8).
Mà 4 = 22; 7 = 7; 8 = 23.
Suy ra BCNN(4, 7, 8) = 23.7 = 56.
Vậy x = 56.
Câu 9:
 Xem đáp án
Xem đáp án
Ta có x ∈ B(12) = {0; 12; 24; 36; 48; 60; 72; 84; 96; ...}.
Mà 12 < x < 90 nên x ∈ {24; 36; 48; 60; 72; 84}.
Vậy x ∈ {24; 36; 48; 60; 72; 84}.
Câu 10:
Tìm x ∈ BC(12, 15, 20) và x ≤ 500.
 Xem đáp án
Xem đáp án
Ta có: 12 = 22.3; 15 = 3.5 và 20 = 22.5.
Suy ra BCNN(12, 15, 20) = 22.3.5 = 60.
Suy ra x ∈ B(60) = {0; 60; 120; 180; 240; 300; 360; 420; 480; 540; 600; ...}.
Mà x ≤ 500 nên x ∈ {0; 60; 120; 180; 240; 300; 360; 420; 480}.
Vậy x ∈ {0; 60; 120; 180; 240; 300; 360; 420; 480}.
Câu 11:
Phân tích các số sau ra thừa số nguyên tố và tìm xem mỗi số có bao nhiêu ước:
a) 320.
b) 625.
c) 504.
d) 900.
e) 3675.
 Xem đáp án
Xem đáp án
a) 320 = 26.5.
Suy ra 320 có (6 + 1).(1 + 1) = 14 ước.
b) 625 = 54.
Suy ra 625 có 4 + 1 = 5 ước.
c) 504 = 23.32.7.
Suy ra 504 có (3 + 1)(2 + 1)(1 + 1) = 24 ước.
d) 900 = 22.32.52.
Suy ra 900 có (2 + 1)(2 + 1)(2 + 1) =27 ước.
e) 3675 = 3.52.72.
Suy ra 3675 có (1 + 1)(2 + 1)(2 + 1) = 18 ước.
Câu 12:
Một bà đi chợ bán trứng, lần đầu bà bán được số trứng, lần thứ hai bà bán được số trứng còn lại, cuối cùng còn lại 10 quả. Hỏi số trứng ban đầu là bao nhiêu quả?
 Xem đáp án
Xem đáp án
Số trứng còn lại sau khi bán lần đầu là: (số trứng ban đầu).
Số trứng lần thứ hai bán được là: (số trứng ban đầu).
Sau hai lần bán, số trứng còn lại là: (số trứng ban đầu).
Số trứng ban đầu là: (quả trứng).
Đáp số: 50 quả trứng.
Câu 13:
 Xem đáp án
Xem đáp án
Ta có sơ đồ:
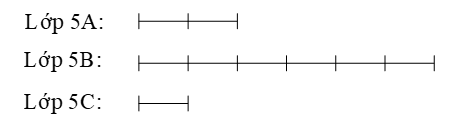
Tổng số cây 3 lớp trồng được là: 603 cây.
Quan sát sơ đồ, ta có tổng số phần bằng nhau là: 2 + 6 + 1 = 9 (phần).
Số cây lớp 5A trồng được là: 603 : 9 ⨯ 2 = 134 (cây).
Số cây lớp 5B trồng được là: 603 : 9 ⨯ 6 = 402 (cây).
Số cây lớp 5C trồng được là: 603 : 9 ⨯ 1 = 67 (cây).
Đáp số: Lớp 5A: 134 cây;
Lớp 5B: 402 cây;
Lớp 5C: 67 cây.
Câu 14:
Tính: 1.32 + 3.52 + 5.72 + ... + 97.992.
 Xem đáp án
Xem đáp án
Đặt A = 1.32 + 3.52 + 5.72 + ... + 97.992.
= 1.3.3 + 3.5.5 + 5.7.7 + ... + 97.99.99.
= 1.3.(5 – 2) + 3.5.(7 – 2) + 5.7.(9 – 2) + ... + 97.99.(101 – 2).
= (1.3.5 – 1.3.2) + (3.5.7 – 3.5.2) + (5.7.9 – 5.7.2) + ... + (97.99.101 – 97.99.2).
= (1.3.5 + 3.5.7 + 5.7.9 + ... + 97.99.101) – 2.(1.3 + 3.5 + 5.7 + ... + 97.99).
Đặt M = 1.3.5 + 3.5.7 + 5.7.9 + ... + 97.99.101 và N = 1.3 + 3.5 + 5.7 + ... + 97.99.
Ta có 8M = 1.3.5.8 + 3.5.7.(9 – 1) + 5.7.9.(11 – 3) + ... + 97.99.101.(103 – 95).
= 1.3.5.8 + (3.5.7.9 – 1.3.5.7) + (5.7.9.11 – 3.5.7.9) + ... + (97.99.101.103 – 95.97.99.101.
= 1.3.5.8 – 1.3.5.7 + 97.99.101.103
= 1.3.5.(8 – 7) + 97.99.101.103
= 15 + 97.99.101.103.
Suy ra .
Lại có 6N = 1.3.6 + 3.5.6 + 5.7.6 + ... + 97.99.6
= 1.3.(5 + 1) + 3.5.(7 – 1) + 5.7.(9 – 3) + ... + 97.99.(101 – 95)
= 1.3.5 + 1.3.1 + 3.5.7 – 3.5.1 + 5.7.9 – 5.7.3 + ... + 97.99.101 – 97.99.95
= 1.3.1 + 97.99.101
= 3 + 97.99.101.
Suy ra .
Vì vậy
= 12 164 201.
Vậy A = 12 164 201.
Câu 15:
Tính giá trị của x thỏa mãn 165 – (35 : x + 3) . 19 = 13.
 Xem đáp án
Xem đáp án
Ta có 165 – (35 : x + 3) . 19 = 13.
⇔ (35 : x + 3) . 19 = 165 – 13.
⇔ (35 : x + 3) . 19 = 152.
⇔ 35 : x + 3 = 152 : 19.
⇔ 35 : x + 3 = 8.
⇔ 35 : x = 8 – 3.
⇔ 35 : x = 5.
⇔ x = 35 : 5.
⇔ x = 7.
Vậy x = 7 thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án A.
Câu 16:
Chuyển đổi hỗn số 21 và thành số thập phân.
 Xem đáp án
Xem đáp án
Ta có .
Vậy khi chuyển đổi hỗn số 21 và thành số thập phân, ta được 21,5.
Câu 17:
 Xem đáp án
Xem đáp án
Lần cân thứ nhất:
– Lấy hai đồng xu ra, sau đó chia 6 đồng còn lại thành 2 nhóm, mỗi nhóm có 3 đồng xu.
– Cân 2 nhóm (mỗi nhóm có 3 đồng xu) vừa chia và xem kết quả.
Lần cân thứ hai:
⦁ Trường hợp 1: Nếu cân thăng bằng thì cân 2 đồng xu được lấy ra ở bước 1, phía cân nào nhẹ hơn thì bên đó là đồng xu giả.
⦁ Trường hợp 2: Nếu cân không thăng bằng thì lấy 3 đồng xu bên cân nhẹ hơn, bỏ 1 đồng ra và cân 2 đồng còn lại. Nếu cân thăng bằng thì đồng xu vừa bỏ ra là đồng xu giả. Nếu cân không thăng bằng thì đồng xu bên cân nhẹ hơn là đồng xu giả.
Câu 18:
Cho A = 5 + 52 + 53 + ... + 5100.
a) Số A là số nguyên tố hay hợp số?
b) Số A có phải là số chính phương không?
 Xem đáp án
Xem đáp án
a) Ta có 5 ⋮ 5; 52 ⋮ 5; 53 ⋮ 5; ...; 599 ⋮ 5 và 5100 ⋮ 5.
Suy ra A = 5 + 52 + 53 + ... + 5100 chia hết cho 5 (1)
Vậy A là hợp số.
b) Ta có 5 không chia hết cho 52; 52 ⋮ 52; 53 ⋮ 52; ...; 599 ⋮ 52 và 5100 ⋮ 52.
Suy ra A = 5 + 52 + 53 + ... + 5100 không chia hết cho 52 (2)
Từ (1), (2), suy ra A không phải là số chính phương.
Câu 19:
Cho H, K là các giao điểm của đường tròn (O1), (O2). Đường thẳng O1H cắt (O1) tại A, (O2) tại B. O2H cắt (O1) tại C và (O2) tại D. Chứng minh rằng ba đường thẳng AC, BD, HK đồng quy tại 1 điểm.
 Xem đáp án
Xem đáp án
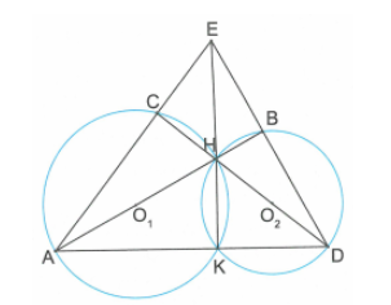
Gọi E là giao điểm của AC và BD.
Vì các tam giác ACH, AKH nội tiếp đường tròn (O1) có cạnh HA là đường kính nên tam giác ACH vuông tại C và tam giác AKH vuông tại K.
Suy ra
Vì các tam giác HDK, HDB nội tiếp đường tròn (O2) có cạnh HD là đường kính nên tam giác HDK vuông tại K và tam giác HBD vuông tại B.
Suy ra
Từ (2), (4), suy ra ba điểm A, K, D thẳng hàng.
Do đó HK ⊥ AD.
Từ (1), (3), suy ra H là trực tâm của tam giác AED.
Do đó HE ⊥ AD.
Vì vậy H ∈ EK.
Vậy ba đường thẳng AC, BD, HK đồng quy tại 1 điểm.
Câu 20:
 Xem đáp án
Xem đáp án
Với p = 3, ta có:
⦁ 8p – 1 = 23 là số nguyên tố;
⦁ 8p + 1 = 25 không phải là số nguyên tố.
Với p ≠ 3, ta có: p không chia hết cho 3 nên 8p không chia hết cho 3.
Ta có 8p(8p – 1)(8p + 1) là tích của 3 số tự nhiên liên tiếp.
Suy ra 8p(8p – 1)(8p + 1) chia hết cho 3.
Lại có 8p – 1 > 3 (p ∈ ℕ).
Suy ra 8p – 1 không chia hết cho 3.
Do đó 8p + 1 chia hết cho 3.
Mà 8p + 1 > 3, p ∈ ℕ.
Suy ra 8p + 1 là hợp số.
Vậy 8p + 1 là hợp số; 8p – 1 là số nguyên tố.
Câu 21:
Cho tam giác ABC có , và là các góc nhọn, M là một điểm thuộc BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đối xứng với M qua AC. Gọi I, K là giao điểm của DE với AB, AC.
a) Tính các góc của tam giác DAE.
 Xem đáp án
Xem đáp án
a)
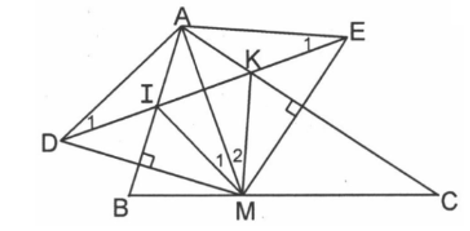
Ta có D là điểm đối xứng với M qua AB (giả thiết).
Suy ra AB là đường trung trực của đoạn DM.
Do đó AD = AM.
Vì vậy tam giác ADM cân tại A.
Suy ra AB vừa là đường trung trực, vừa là đường phân giác của tam giác ADM.
Do đó .
Chứng minh tương tự, ta được .
Ta có .
Ta có:
⦁ AB là đường trung trực của đoạn DM. Suy ra AD = AM.
⦁ AC là đường trung trực của đoạn EM. Suy ra AM = AE.
Do đó AD = AE.
Vì vậy tam giác ADE cân tại A.
Suy ra .
Vậy và .
Câu 22:
 Xem đáp án
Xem đáp án
b) Ta có AB là đường trung trực của đoạn DM.
Mà I ∈ AB.
Do đó ID = IM.
Vì vậy tam giác IDM cân tại I.
Suy ra .
Chứng minh tương tự, ta được .
Suy ra .
Do đó .
Chứng minh tương tự, ta được .
Mà (câu a).
Suy ra .
Vậy MA là tia phân giác của .
Câu 23:
c) Điểm M nằm ở vị trí nào trên cạnh BC thì DE có độ dài ngắn nhất.
 Xem đáp án
Xem đáp án
c) Từ kết quả câu a, ta thấy tam giác ADE cân tại A có góc ở các đỉnh không đổi nên cạnh đáy DE nhỏ nhất khi và chỉ khi cạnh bên AD nhỏ nhất.
⇔ AM nhỏ nhất.
⇔ M là chân đường vuông góc kẻ từ A đến BC.
Lại có và là các góc nhọn.
Vậy M là chân đường vuông góc kẻ từ A đến BC và M nằm trên cạnh BC.
Câu 24:
Tìm số trung bình cộng của:
a) Các số 7; 9; 11; ...; 19; 21.
b) Các số tròn chục có hai chữ số.
 Xem đáp án
Xem đáp án
a) Dãy số là: 7; 9; 11; ...; 19; 21.
Số số hạng của dãy số trên là: (21 – 7) : 2 + 1 = 8 (số hạng).
Tổng của dãy số trên là: (7 + 21) ⨯ 8 : 2 = 112.
Trung bình cộng của dãy số trên là: 112 : 8 = 14.
Đáp số: 14.
b) Các số tròn chục có hai chữ số là: 10; 20; 30; ...; 80; 90.
Số số hạng của dãy số trên là: (90 – 10) : 2 + 1 = 41 (số hạng).
Tổng của dãy số trên là: (10 + 90) ⨯ 41 : 2 = 2050.
Trung bình cộng của dãy số trên là: 2050 : 41 = 50.
Đáp số: 50.
Câu 25:
Một cửa hàng có 32,8 tạ gạo, ngày thứ nhất cửa hàng bán được số gạo, ngày thứ hai cửa hàng bán được số gạo còn lại. Hỏi cửa hàng còn lại bao nhiêu kg gạo chưa bán?
 Xem đáp án
Xem đáp án
Số gạo cửa hàng bán được ở ngày thứ nhất là: (tạ gạo).
Số gạo cửa hàng còn lại sau ngày thứ nhất là: 32,8 – 24,6 = 8,2 (tạ gạo).
Số gạo cửa hàng bán được ở ngày thứ hai là: (tạ gạo).
Số gạo cửa hàng chưa bán là: 8,2 – 6,15 = 2,05 (tạ gạo).
Đổi: 2,05 tạ = 205 kg.
Đáp số: 205 kg gạo.
Câu 26:
Để đánh số các trang của một quyển sách, người ta phải dùng tất cả 900 chữ số. Hỏi quyển sách đó có bao nhiêu trang?
 Xem đáp án
Xem đáp án
99 trang đầu cần dùng: 9 × 1 + 90 × 2 = 189 (chữ số).
999 trang đầu cần dùng: 9 × 1 + 90 × 2 + 900 × 3 = 2889 (chữ số).
Vì 189 < 900 < 2889 nên trang cuối cùng phải có 3 chữ số.
Số chữ số để đánh số các trang có 3 chữ số là: 900 – 189 = 711 (chữ số).
Số trang có 3 chữ số là: 711 : 3 = 237 (trang).
Quyển sách đó có tất cả số trang là: 99 + 237 = 336 (trang).
Đáp số: 336 trang.
Câu 27:
Một quyển sách giảm giá đi 20% giá ban đầu. Vậy giá mới phải tăng bao nhiêu phần trăm để được trở về như giá ban đầu.
 Xem đáp án
Xem đáp án
Giá của quyển sách giảm đi 20% tức là giảm đi của nó.
Ta có sơ đồ:
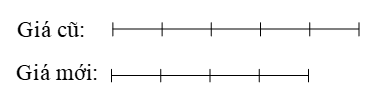
Vậy giá mới phải tăng thêm để được trở về như giá ban đầu.
Câu 28:
Hai năm trước, tuổi mẹ hơn tổng số tuổi của hai con là 25 tuổi. Hỏi ba năm sau, tuổi mẹ hơn tổng số tuổi của hai con là bao nhiêu tuổi?
 Xem đáp án
Xem đáp án
Ba năm sau (tức là sau 5 năm), mẹ thêm 5 tuổi và tổng số tuổi của hai con thêm 10 tuổi.
Vậy ba năm sau, tuổi mẹ hơn tổng số tuổi của hai con là: 25 – (10 – 5) = 20 (tuổi).
Đáp số: 20 tuổi.
Câu 29:
Hiện nay mẹ 45 tuối. Mẹ hơn con 29 tuổi. Hỏi tổng số tuổi của hai mẹ con là bao nhiêu?
 Xem đáp án
Xem đáp án
Tuổi của con hiện nay là:
45 – 29 = 16 (tuổi)
Tổng số tuổi của hai mẹ con là:
45 + 16 = 61 (tuổi)
Đáp số: 61 tuổi.
Câu 30:
Mẹ hơn con 28 tuổi. Hiện nay tuổi con bằng tuổi mẹ. Hỏi hiện nay mỗi người bao nhiêu tuổi?
 Xem đáp án
Xem đáp án
Hiệu số phần bằng nhau là: 5 – 1 = 4 (phần).
Giá trị của một phần là: 28 : 4 = 7 (tuổi).
Tuổi mẹ hiện nay là: 7 × 5 = 35 (tuổi).
Tuổi con hiện nay là: 7 × 1 = 7 (tuổi).
Đáp số: Mẹ: 35 tuổi;
Con: 7 tuổi.
Câu 31:
Một khu rừng hình chữ nhật có chu vi 5 km 60 dam. Chiều dài hơn chiều rộng 800 m.
a) Hỏi diện tích khu rừng đó bằng bao nhiêu ha? Bao nhiêu m2?
 Xem đáp án
Xem đáp án
a) Đổi: 5 km 60 dam = 5600 m.
Nửa chu vi khu rừng đó là: 5600 : 2 = 2800 (m).
Chiều rộng khu rừng đó là: (2800 – 800) : 2 = 1000 (m).
Chiều dài khu rừng đó là: 1000 + 800 = 1800 (m).
Diện tích khu rừng đó là: 1800 × 1000 = 1 800 000 (m2).
Đổi: 1 800 000 m2 = 180 ha.
Câu 32:
b) Biết diện tích khu rừng trồng cây mới. Tính tỉ số diện tích trồng cây mới và phần diện tích còn lại của khu rừng.
 Xem đáp án
Xem đáp án
b) Diện tích phần còn lại của khu rừng chiếm: (diện tích khu rừng).
Tỉ số diện tích trồng cây mới và phần diện tích còn lại của khu rừng là: .
Đáp số: 180 ha; 1 800 000 m2 và .
Câu 33:
Một hình vuông có chu vi là 1 m 4 cm. Một hình chữ nhật có trung bình cộng độ dài hai cạnh bằng độ dài cạnh hình vuông và có chiều dài gấp 3 lần chiều rộng. Hỏi diện tích nào lớn hơn và lớn hơn bao nhiêu cm2?
 Xem đáp án
Xem đáp án
Đổi: 1 m 4 cm = 104 cm.
Cạnh hình vuông là: 104 : 4 = 26 (cm).
Tổng hai cạnh của hình chữ nhật là: 26 × 2 = 52 (cm).
Tổng số phần bằng nhau là: 3 + 1 = 4 (phần).
Chiều dài hình chữ nhật là: 52 : 4 × 3 = 39 (cm).
Chiều rộng hình chữ nhật là: 52 : 4 × 1 = 13 (cm).
Diện tích hình chữ nhật là: 39 × 13 = 507 (cm2).
Diện tích hình vuông là: 26 × 26 = 676 (cm2).
Ta có 676 cm2 > 507 cm2 676 – 507 = 169 (cm2).
Vậy diện tích hình vuông lớn hơn diện tích hình chữ nhật và lớn hơn 169 cm2.
Câu 34:
Một cửa hàng giảm 20% giá mặt hàng trong dịp lễ. Sau đó, cửa hàng cần tăng lên bao nhiêu phần trăm giá sau khi giảm để đưa giá mặt hàng về ban đầu?
 Xem đáp án
Xem đáp án
Giá của mặt hàng giảm 20% tức là giảm của nó.
Ta có sơ đồ:
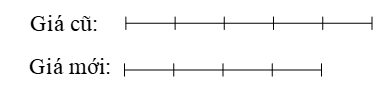
Vậy cửa hàng đó cần tăng thêm giá sau khi giảm để đưa giá mặt hàng về ban đầu.
Câu 35:
Số học sinh bốn khối 6, 7, 8, 9 tỉ lệ với các số 9, 8, 7, 6. Biết rằng số học sinh khối 9 ít hơn số học sinh khối 7 là 70 học sinh. Tìm số học sinh mỗi khối.
 Xem đáp án
Xem đáp án
Gọi số học sinh các khối 6, 7, 8, 9 lần lượt là x, y, z, t (học sinh).
Điều kiện: x, y, z, t ∈ ℕ*.
Ta có số học sinh khối 9 ít hơn số học sinh khối 7 là 70 học sinh, nghĩa là y – t = 70.
Lại có học sinh bốn khối 6, 7, 8, 9 tỉ lệ với các số 9, 8, 7, 6, nghĩa là .
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được: .
Với , ta có: x = 9.35 = 315 (học sinh).
Với , ta có: y = 8.35 = 280 (học sinh).
Với , ta có: z = 7.35 = 245 (học sinh).
Với , ta có: t = 6.35 = 210 (học sinh).
Vậy số học sinh của các khối 6, 7, 8, 9 lần lượt là 315 học sinh; 280 học sinh; 245 học sinh; 210 học sinh.
Câu 36:
Cho tam giác ABC nhọn có AB = 6, BC = 7, AC = 8. Tính độ dài đường cao AH.
 Xem đáp án
Xem đáp án
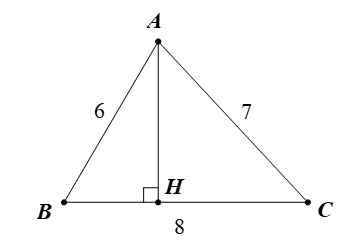
Theo định lí côsin, ta có: .
Tam giác ABH vuông tại H:
⦁ .
⦁ .
Suy ra .
Vậy .
Câu 37:
 Xem đáp án
Xem đáp án
Vì 126 ⋮ x và 210 ⋮ x nên x ∈ ƯC(126, 210).
Ta có 126 = 2.32.7 và 210 = 2.3.5.7.
Suy ra ƯCLN(126, 210) = 2.3.7 = 42.
Do đó ƯC(126, 210) = {1; 2; 3; 6; 7; 14; 21; 42}.
Vì 15 < x < 30 và x là số tự nhiên nên x = 21.
Vậy x = 21 thỏa mãn yêu cầu bài toán.
Câu 38:
Tìm số lớn nhất có 3 chữ số biết khi chia cho 75 thì thương và số dư bằng nhau.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là (a ≠ 0; a, b, c là các chữ số từ 0 đến 9).
Gọi k là thương hay số dư khi chia cho 75 (k ∈ ℕ*).
Tức là, dư k.
Hay .
Vì lớn nhất nên 76k là số lớn nhất có 3 chữ số.
Lại có 1000 : 75 = 13,3333...
Suy ra k = 13.
Khi đó .
Vậy số cần tìm là 988.
Câu 39:
Tìm số nguyên tố p sao cho:
a) p + 4; p + 8 là số nguyên tố.
 Xem đáp án
Xem đáp án
a) Với p = 2, ta có: p + 4 = 6 và p + 8 = 10 không phải là số nguyên tố.
Với p = 3, ta có: p + 4 = 7 và p + 8 = 11 là số nguyên tố.
Nếu p > 3 và p là số nguyên tố thì p = 3k + 1 hoặc p = 3k + 2 (k ∈ ℕ*).
Ta thấy:
⦁ Nếu p = 3k + 1 thì p + 8 = 3k + 1 + 8 = 3k + 9 = 3(k + 3) là một số chia hết cho 3 (loại).
⦁ Nếu p = 3k + 2 thì p + 4 = 3k + 2 + 4 = 3k + 6 = 3(k + 2) là một số chia hết cho 3 (loại).
Vậy ta đã chứng minh được p = 3 là giá trị duy nhất thỏa mãn yêu cầu bài toán.
Câu 40:
Tìm số nguyên tố p sao cho:
b) p + 4; p + 14 là số nguyên tố.
 Xem đáp án
Xem đáp án
b) Với p = 2, ta có: p + 4 = 6 và p + 8 = 10 không phải là số nguyên tố.
Với p = 3, ta có: p + 4 = 7 và p + 14 = 17 là số nguyên tố.
Nếu p > 3 và p là số nguyên tố thì p = 3k + 1 hoặc p = 3k + 2 (k ∈ ℕ*).
Ta thấy:
⦁ Nếu p = 3k + 1 thì p + 14 = 3k + 1 + 14 = 3k + 15 = 3(k + 5) là một số chia hết cho 3 (loại).
⦁ Nếu p = 3k + 2 thì p + 4 = 3k + 2 + 4 = 3k + 6 = 3(k + 2) là một số chia hết cho 3 (loại).
Vậy ta đã chứng minh được p = 3 là giá trị duy nhất thỏa mãn yêu cầu bài toán.
Câu 41:
Tìm số nguyên tố p sao cho p + 6; p + 12; p + 18; p + 24 đều là các số nguyên tố.
 Xem đáp án
Xem đáp án
Với p = 2, ta có: p + 6 = 8 không phải là số nguyên tố.
Với = 3, ta có: p + 6 = 9 không phải là số nguyên tố.
Với p = 5, ta có: p + 6 = 11; p + 12 = 17; p + 18 = 23; p + 24 = 29 đều là các số nguyên tố.
Nếu p > 5 và p là số nguyên tố thì p = 5k + 1 hoặc p = 5k + 2 hoặc p = 5k + 3 hoặc p = 5k + 4 (k ∈ ℕ*).
⦁ Nếu p = 5k + 1 thì p + 24 = 5k + 1 + 24 = 5k + 25 = 5(k + 5) là một số chia hết cho 5 (loại).
⦁ Nếu p = 5k + 2 thì p + 18 = 5k + 2 + 18 = 5k + 20 = 5(k + 4) là một số chia hết cho 5 (loại).
⦁ Nếu p = 5k + 3 thì p + 12 = 5k + 3 + 12 = 5k + 15 = 5(k + 3) là một số chia hết cho 5 (loại).
⦁ Nếu p = 5k + 4 thì p + 6 = 5k + 4 + 6 = 5k + 10 = 5(k + 2) là một số chia hết cho 5 (loại).
Vậy ta đã chứng minh được p = 5 là giá trị duy nhất thỏa mãn yêu cầu bài toán.
Câu 42:
Tính các góc của hình thang ABCD (AB // CD) biết rằng , .
 Xem đáp án
Xem đáp án
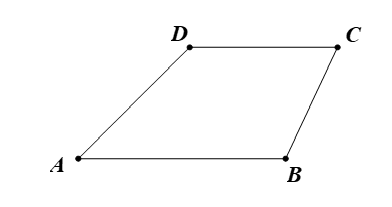
Hình thang ABCD, có: AB // CD.
Suy ra (cặp góc trong cùng phía).
Do đó .
Vì vậy .
Suy ra .
Với , ta có: .
Theo đề, ta có: .
Suy ra .
Hình thang ABCD, có: AB // CD.
Suy ra (cặp góc trong cùng phía).
Do đó .
Vì vậy .
Suy ra .
Với , ta có: .
Vậy ; ; và .
Câu 43:
Tính nhanh: 1.2 + 2.3 + 3.4 + ... + 98.99.
 Xem đáp án
Xem đáp án
Đặt A = 1.2 + 2.3 + 3.4 + ... + 98.99.
Suy ra 3A = 1.2.3 + 2.3.3 + 3.4.3 + ... + 98.99.3.
= 1.2.3 + 2.3.(4 – 1) + 3.4.(5 – 2) + ... + 98.99.(100 – 97).
= 1.2.3 + 2.3.4 – 1.2.3 + 3.4.5 – 2.3.4 + ... + 98.99.100 – 97.98.99.
= 98.99.100
Suy ra A = 98.99.100 : 3 = 98.33.100 = 323 400.
Vậy A = 323 400.
Câu 44:
 Xem đáp án
Xem đáp án
Đặt A = 1.4 + 2.5 + 3.6 + ... + 100.103.
= 1.(2 + 2) + 2.(3 + 2) + 3.(4 + 2) + ... + 100.(101 + 2).
= 1.2 + 2.3 + 3.4 + ... + 100.101 + (1.2 + 2.2 + 3.2 + ... + 100.2).
= 1.2 + 2.3 + 3.4 + ... + 100.101 + 2(1 + 2 + 3 + ... + 100).
Đặt M = 1.2 + 2.3 + 3.4 + ... + 100.101.
Suy ra 3M = 1.2.3 + 2.3.3 + 3.4.3 + ... + 100.101.3.
= 1.2.3 + 2.3.(4 – 1) + 3.4.(5 – 2) + ... + 100.101.(102 – 99).
= 1.2.3 + 2.3.4 – 1.2.3 + 3.4.5 – 2.3.4 + ... + 100.101.102 – 99.100.101.
= 100.101.102.
Suy ra M = 100.101.102 : 3 = 100.101.34 = 343 400.
Đặt N = 1 + 2 + 3 + ... + 100 = (1 + 100) × 100 : 2 = 5050.
Vậy A = M + 2N = 343 400 + 2.5050 = 353 500.
Vậy A = 353 500.
Câu 46:
 Xem đáp án
Xem đáp án
Số lẻ đầu tiên là 1.
Số lẻ cuối cùng là: 1 + (20 – 1) × 2 = 39.
Tổng của 20 số tự nhiên lẻ liên tiếp đầu tiên là: (1 + 39) × 20 : 2 = 400.
Đáp số: 400.
Câu 47:
Tìm số tự nhiên x, biết: x ∈ BC(7, 14, 21) và x < 210.
 Xem đáp án
Xem đáp án
Ta có 7 = 7; 14 = 2.7 và 21 = 3.7.
Suy ra BCNN(7, 14, 21) = 2.3.7 = 42.
Do đó x ∈ BC(7, 14, 21) = {0; 42; 84; 126; 168; 210; 252;...}.
Mà x < 210 nên x ∈ {0; 42; 84; 126; 168}.
Vậy x ∈ {0; 42; 84; 126; 168}.
Câu 48:
Giải phương trình x4 = 12x + 5.
 Xem đáp án
Xem đáp án
Ta có x4 = 12x + 5.
⇔ x4 – 12x – 5 = 0.
⇔ x4 – 2x3 – x2 + 2x3 – 4x2 – 2x + 5x2 – 10x – 5 = 0.
⇔ x2(x2 – 2x – 1) + 2x(x2 – 2x – 1) + 5(x2 – 2x – 1) = 0.
⇔ (x2 – 2x – 1)(x2 + 2x + 5) = 0 (*)
Ta có (x + 1)2 ≥ 0, ∀x ∈ ℝ.
⇔ x2 + 2x + 1 ≥ 0, ∀x ∈ ℝ.
⇔ x2 + 2x + 5 ≥ 4 > 0, ∀x ∈ ℝ.
Khi đó phương trình (*) tương đương với x2 – 2x – 1 = 0.
.
Vậy tập nghiệm của phương trình đã cho là: .
Câu 49:
 Xem đáp án
Xem đáp án
Ta có (x2 + 2)2 – 6(x2 + 2) + 9 = 0 (1)
Đặt t = x2 + 2, t > 0.
Phương trình (1) tương đương với: t2 – 6t + 9 = 0.
⇔ t = 3 (nhận).
Với t = 3, ta có: x2 + 2 = 3.
⇔ x2 – 1 = 0.
⇔ (x – 1)(x + 1) = 0.
⇔ x – 1 = 0 hoặc x + 1 = 0.
⇔ x = 1 hoặc x = –1.
Vậy tập nghiệm của phương trình đã cho là: S = {1; –1}.
Câu 50:
Tính tổng: 1 + 22 + 32 + ... + 992 + 1002.
 Xem đáp án
Xem đáp án
Đặt A = 1 + 22 + 32 + ... + 992 + 1002.
= 1.1 + 2.2 + 3.3 + ... + 99.99 + 100.100.
= 1.(2 – 1) + 2.(3 – 1) + 3.(4 – 1) + ... + 99.(100 – 1) + 100.(101 – 1).
= 1.2 – 1 + 2.3 – 2 + 3.4 – 3 + ... + 99.100 – 1.99 + 100.101 – 100.
= (1.2 + 2.3 + 3.4 + ... + 99.100 + 100.101) – (1 + 2 + 3 + ... + 100).
Đặt B = 1.2 + 2.3 + 3.4 + ... + 99.100 + 100.101.
Suy ra 3B = 1.2.3 + 2.3.3 + 3.4.3 + ... + 99.100.3 + 100.101.3.
= 1.2.3 + 2.3.(4 – 1) + 3.4.(5 – 2) + ... + 99.100.(101 – 98) + 100.101.(102 – 99).
= 1.2.3 + 2.3.4 – 1.2.3 + 3.4.5 – 2.3.4 + ... + 99.100.101 – 98.99.100 + 100.101.102 – 99.100.101.
= 100.101.102.
Suy ra B = 100.101.102 : 3 = 100.101.34 = 343 400.
Đặt C = 1 + 2 + 3 + ... + 100 = (1 + 100) × 100 : 2 = 5050.
Vậy A = B – C = 343 400 – 5050 = 338 350.
Câu 51:
Phân tích đa thức thành nhân tử:
a) a2 – 9.
b) 9a2 – 1.
 Xem đáp án
Xem đáp án
a) a2 – 9 = a2 – 32 = (a – 3)(a + 3).
b) 9a2 – 1 = (3a)2 – 12 = (3a – 1)(3a + 1).
Câu 52:
Phân tích đa thức thành nhân tử:
c) 36x2 – 49y2.
d) .
 Xem đáp án
Xem đáp án
c) 36x2 – 49y2 = (6x)2 – (7y)2 = (6x – 7y)(6x + 7y).
d) .