Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 23)
-
2066 lượt thi
-
60 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Trung bình cộng của 4 số bằng 25 .Trung bình cộng của 3 số đầu bằng 22. Trung bình cộng của 3 số cuối bằng 20. Tìm trung bình cộng của số thứ 2 và số thứ 3?
 Xem đáp án
Xem đáp án
Tổng của 4 số là: 25 × 4 = 100
Tổng của 3 số đầu là: 22 × 3 = 66
Tổng của 3 số cuối là: 20 × 3 = 60
Số thứ nhất là: 100 − 60 = 40
Số thứ tư là: 100 − 66 = 34
Tổng của số thứ hai và số thứ ba là: 100 − (40 + 34) = 26
Trung bình cộng của số thứ 2 và số thứ ba là: 26 : 2 = 13
Đáp số: 13.
Câu 2:
Trung bình cộng của 4 số là 20, biết trung bình cộng của 3 số đầu là 25. Số thứ tư là bao nhiêu?
 Xem đáp án
Xem đáp án
Tổng bốn số là: 20 × 4 = 80
Tổng ba số đầu là: 25 × 3 = 75
Số thứ tư là: 80 − 75 = 5
Đáp số: 5.
Câu 3:
Trung bình cộng của ba số là 120, biết rằng số thứ ba bằng trung bình cộng của hai số còn lại. Tìm số thứ ba?
 Xem đáp án
Xem đáp án
Tổng của ba số là: 120 × 3 = 360
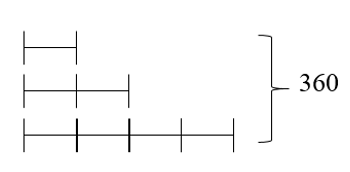
Tổng số phần là: 1 + 4 = 5 (phần)
Số thứ ba là: 360 : 5 = 72
Đáp số: 72.
Câu 4:
Trung bình cộng của ba số là 21. Tìm ba số đó biết số thứ ba gấp 3 lần số thứ 2, số thứ hai gấp 2 lần số thứ nhất?
 Xem đáp án
Xem đáp án
Tổng của ba số là: 21 × 3 = 63
Vì số thứ ba gấp 3 lần số thứ hai và số thứ hai gấp 2 lần số thứ nhất nên số thứ ba gấp 6 lần số thứ nhất.
Ta có sơ đồ:
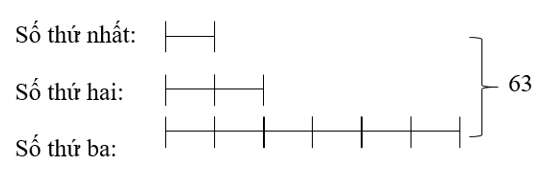
Theo sơ đồ, tổng số phần bằng nhau là: 1 + 2 + 6 = 9 (phần)
Số thứ nhất là: 63 : 9 = 7
Số thứ hai là: 7 × 2 = 14
Số thứ ba là: 7 × 6 = 42
Đáp số: Số thứ nhất: 7;
Số thứ hai là 14;
Câu 5:
Tìm trung bình cộng của các số tự nhiên nhỏ hơn 1025.
 Xem đáp án
Xem đáp án
Dãy các số tự nhiên nhỏ hơn 1 025 là: 0; 1; 2; ….; 1 024.
Số số hạng của dãy là: (1 024 – 0) : 1 + 1 = 1 025 (số hạng)
Tổng các số của dãy là: (1 024 + 0) × 1025 : 2 = 524 800
Trung bình cộng của các số tự nhiên nhỏ hơn 1025 là: 524 800 : 1 025 = 512.
Đáp số: 512.
Câu 6:
Trung bình cộng của hai số bằng 2016. Nếu tăng số thứ nhất lên 3 lần thì trung bình cộng của chúng bằng 4125. Tìm số thứ nhất.
 Xem đáp án
Xem đáp án
Tổng của hai số ban đầu là: 2 016 × 2 = 4 032
Tổng của hai số sau khi tăng số thứ nhất lên 3 lần là: 4 125 × 2 = 8 250
Phần tăng thêm chính là hai lần số thứ nhất.
Hai lần số thứ nhất là: 8 250 – 4 032 = 4 218
Số thứ nhất là: 4 218 : 2 = 2 019.
Đáp số: 2 019.
Câu 7:
Trung bình cộng của ba số bằng 34. Nếu tăng số thứ nhất gấp hai lần thì trung bình cộng của chúng bằng 38. Nếu tăng số thứ hai gấp 3 lần thì trung bình cộng của chúng bằng 46. Tìm số thứ nhất và số thứ hai.
 Xem đáp án
Xem đáp án
Tổng của ba số là: 34 × 3 = 102
Tổng của ba số khi số thứ nhất gấp hai lần là: 38 × 3 = 114
Phần tăng thêm chính là số thứ nhất: 114 – 102 = 12
Tổng của ba số khi số thứ hai gấp 3 lần là: 46 × 3 = 138
Phần tăng thêm chính là hai lần số thứ hai
Hai lần số thứ hai là: 138 – 102 = 36
Số thứ hai là: 36 : 2 = 18
Đáp số: Số thứ nhất: 12;
Số thứ hai là 18.
Câu 8:
Cho tỉ lệ thức và x.y = 112. Tìm x và y?
 Xem đáp án
Xem đáp án
Ta có: hay (1)
Thay x.y = 112 vào (1), ta được:
hoặc
⇒ x = 8 hoặc x = −8.
• • Với x = 8 thì y = 14.
• Với x = −8 thì y = −14.
Vậy ta có: x = 8; y = 14 hoặc x = −8; y = −14.
Câu 9:
Biết và x + y = 60. Hai số x, y lần lượt là:
 Xem đáp án
Xem đáp án
Ta có
Theo tính chất dãy tỉ số bằng nhau, ta có:
.
Suy ra x = 9 . 3 = 27; y = 11 . 3 = 33
Câu 10:
Tổng của hai số là 80. Số thứ nhất bằng số thứ hai. Tìm hai số đó?
 Xem đáp án
Xem đáp án
Ta có sơ đồ

Theo sơ đồ, tổng số phần bằng nhau là: 7 + 9 = 16 (phần)
Số thứ nhất là: 80 : 16 × 7 = 35
Số thứ hai là: 80 – 35 = 45
Đáp số: Số thứ nhất: 35;
Số thứ hai: 45.
Câu 11:
Cho M = 1 + 3 + 32 + 33 + 34 + …+ 399 + 3100.
a) Tìm số dư khi chia M cho 13.
 Xem đáp án
Xem đáp án
a) Ta có: M = 1 + 3 + 32 + 33 + 34 + …+ 399 + 3100
= (1 + 3) + (32 + 33 + 34) + …+ (398 + 399 + 3100)
= 4 + 32 . (1 + 3 + 32) + …+ 398 . ( 1 + 3 + 32)
4 + (32 + …+ 398) . 13
Do đó M chia cho 13 ta được số dư là 4.
Câu 12:
b) Tìm số dư khi chia M cho 40.
 Xem đáp án
Xem đáp án
b) Ta có: M = 1 + 3 + 32 + 33 + 34 + …+ 399 + 3100
= 1 + (3 + 32 + 33 + 34) + …+ (397 + 398 + 399 + 3100)
= 1 + 3.(1 + 3 + 32 + 33) + …+ 397 . ( 1 + 3 + 32 + 33)
= 1 + (3 + …+ 397) . 40
Do đó M chia cho 40 ta được số dư là 1.
Câu 13:
 Xem đáp án
Xem đáp án
Ta có M = 1 + 3 + 32 + 33 + …+ 311 + 312
Suy ra 3M = 3 + 32 + 33 + …+ 312 + 313
Do đó 3M – M = 313 – 1
Hay 2M = 313 – 1
Do đó .
Câu 14:
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y = −x2 và đường thẳng (d): y = 3mx – 3 (với m là tham số). Xác định các giá trị của m để (d) cắt (P) tại hai điểm phân biệt sao cho tổng 2 tung độ của hai giao điểm đó bằng −10.
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của đường thẳng (d) và Parabol (P) là:
−x2 = 3mx – 3 x2 + 3mx – 3 = 0 (*)
Ta có ∆ = 9m2 + 12 > 0, ∀m nên phương trình (*) có hai nghiệm phân biệt.
Do đó, (d) cắt (P) tại hai điểm phân biệt (x1; y1) và (x2; y2)
Theo định lý vi ét, có x1 + x2 = −3m; x1x2 = −3
Theo đề bài ta có: y1 + y2 = −10
−x12 – x22 = −10
(x1 + x2)2 – 2x1x2 = 10
9m2 + 6 = 10
hoặc .
Vậy là giá trị cần tìm.
Câu 15:
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y = x2 và đường thẳng (d): y = 2mx – 2m + 3 (với m là tham số).
a) Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt A và B.
 Xem đáp án
Xem đáp án
a) Phương trình hoành độ giao điểm của đường thẳng (d) và Parabol (P) là:
x2 = 2mx – 2m + 3 x2 − 2mx + 2m − 3 = 0 (*)
Ta có ∆' = m2 − (2m − 3) = m2 − 2m + 1 + 2
= (m − 1)2 + 2 > 0, ∀m nên phương trình (*) có hai nghiệm phân biệt.
Do đó, (d) cắt (P) tại hai điểm phân biệt (x1; y1) và (x2; y2)
Câu 16:
b) Gọi y1, y2 là tung độ của A và B. Tìm m để y1 + y2 < 9.
 Xem đáp án
Xem đáp án
b) Theo định lý Vi-et, ta có: x1 + x2 = 2m; x1x2 = 2m −3
Theo đề y1 + y2 < 9
x12 + x22 < 9
(x1 + x2)2 – 2x1x2 < 9
4m2 – 4m + 6 < 9
4m2 – 4m + 1 < 4
(2m – 1)2 < 4
−2 < 2m – 1 < 2
.
Vậy là giá trị cần tìm.
Câu 17:
Một hình chữ nhật có chu vi là bằng 88 m. Nếu tăng chiều rộng lên 8m thì hình chữ nhật trở thành hình vuông. Tính diện tích hình chữ nhật?
 Xem đáp án
Xem đáp án
Nửa chu vi của hình chữ nhật là:
88 : 2 = 44 (m)
Vì nếu tăng chiều rộng thêm 8 m thì hình chữ nhật trở thành hình vuông nên chiều dài hơn chiều rộng 8 m.
Chiều rộng của hình chữ nhật là:
(44 − 8) : 2 = 18 (m)
Chiều dài của hình chữ nhật là:
44 − 18 = 26 (m)
Diện tích của hình chữ nhật là:
18 × 26 = 468 (m2)
Đáp số : 468 m2.
Câu 18:
Tìm số tự nhiên, biết rằng khi chia 147 và 193 cho n thì số dư lần lượt là 17 và 11.
 Xem đáp án
Xem đáp án
Vì 147 chia cho n dư 17 và 193 chia cho n dư 11 nên ta có:
⇒ n ∈ ƯC(130, 182)
Ta có 130 = 2 . 5 . 13; 182 = 2 . 7 . 13
⇒ ƯCLN(130, 182) = 2 . 13 = 26
⇒ ƯC(130, 182) = Ư(26) = {1; 2; 13; 26}
⇒ n ∈ {1; 2; 13; 26}.
Vậy n ∈ {1; 2; 13; 26}.
Câu 19:
 Xem đáp án
Xem đáp án
Ta có: (5n + 7) ⋮ (3n + 2) ⇒ 3(5n + 7) ⋮ (3n + 2) ⇒ (15n + 21) ⋮ (3n + 2)
Mà (3n + 2) ⋮ (3n + 2) ⇒ 5(3n + 2) ⋮ (3n + 2) ⇒ (15n + 10) ⋮ (3n + 2)
Do đó [(15n + 21) − (15n + 10)] ⋮ (3n + 2) ⇒ 11 ⋮ (3n + 2)
⇒ (3n + 2) ∈ Ư(11) = {± 1; ± 11}
TH1: 3n + 2 = −1 ⇒ n = −1 (TM);
TH2: 3n + 2 = 1 (loại);
TH3: 3n + 2 = −11 (loại);
TH4: 3n + 2 = 11 ⇒ n = 3 (TM).
Vậy n ∈ {−1; 3} là giá trị cần tìm.
Câu 20:
Tìm một số, biết 15% của số đó là 75.
 Xem đáp án
Xem đáp án
Số cần tìm là:
75 : 15% = 500.
Đáp số: 500.
Câu 21:
An chia một số cho 40 được thương là 80 và có dư. Biết số dư là số lớn nhất có thể. Hỏi An chia số nào cho 40?
 Xem đáp án
Xem đáp án
Số dư lớn nhất có thể là 39 vì số chia là 40.
Số mà An cần tìm là: 40 × 80 + 39 = 3239.
Đáp số: 3239.
Câu 22:
Đội tuyển thi đá cầu và đấu cờ vua của Trường Tiểu học Võ Thị Sáu có 22 em, trong đó có 15 em thi đá cầu và 12 em thi đấu cờ vua. Hỏi có bao nhiêu em trong đội tuyển thi đấu cả hai môn ?
 Xem đáp án
Xem đáp án
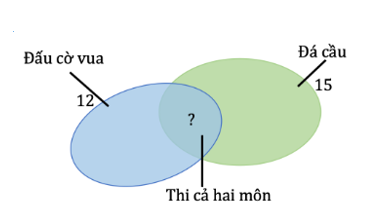
22 – 12 = 10 (em)
Số em trong đội tuyển thi đấu cả hai môn là:
15 – 10 = 5 (em)
Đáp số: 5 em.
Câu 23:
Mỗi hộp kẹo cân nặng 0,25kg; mỗi hộp bánh cân nặng 0,125 kg. Hỏi 15 hộp kẹo và 18 hộp bánh cân nặng bao nhiêu ki - lô - gam?
 Xem đáp án
Xem đáp án
15 hộp kẹo cân nặng là:
0,25 × 15 = 3,75 (kg)
18 hộp bánh cân nặng là:
0,125 × 18 = 2,25 (kg)
15 hộp kẹo và 18 hộp bánh cân nặng là:
3,75 + 2,25 = 6 (kg)
Đáp số: 6 kg.
Câu 24:
Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài với nhau tại A. Vẽ tiếp tuyến chung ngoài BC (B thuộc đường tròn (O), C thuộc đường tròn (O’)). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC tại I.
a) Chứng minh tam giác ABC là tam giác vuông;
 Xem đáp án
Xem đáp án
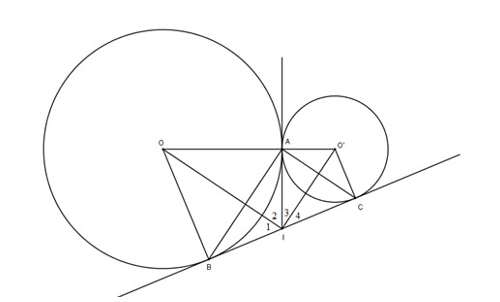
a) Theo tính chất của hai tiếp tuyến cắt nhau, ta có: IA = IB = IC = .
Do đó tam giác ABC vuông tại A.
Câu 25:
b) Tính số đo ;
 Xem đáp án
Xem đáp án
b) Có (theo tính chất hai tiếp tuyến cắt nhau)
Do đó (hai tia phân giác của hai góc kề bù).
Câu 26:
c) Tính độ dài BC, biết OA = 9 cm, O’A = 4 cm.
 Xem đáp án
Xem đáp án
c) Có AI OO’.
Xét tam giác OIO’ vuông tại I, ta có:
IA2 = OA.O’A = 9 . 4 = 36 ⇒ IA = 6.
Do đó BC = 2.IA = 2 . 6 = 12 (cm).
Câu 27:
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung trong tại A cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE.
a) Tứ giác AMIN là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
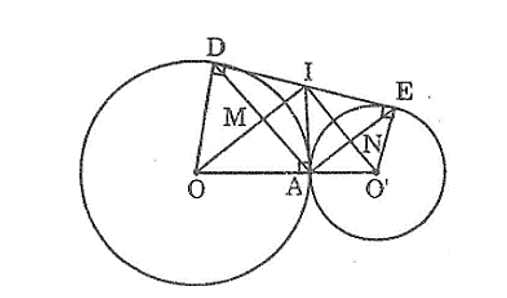
a) Trong đường tròn (O) ta có OI là tia phân giác của (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có O’I là tia phân giác của (tính chất hai tiếp tuyến cắt nhau)
⇒ IO ⊥ IO’ (tính chất hai góc kề bù)
Suy ra hay
Lại có: IA = ID (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác ADI cân tại I
Tam giác cân AID có IO là phân giác của nên IO cũng là đường cao của tam giác AID
Suy ra: IO ⊥ AD hay
Mặt khác: IA = IE (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AEI cân tại I
Tam giác cân AIE có IO’ là phân giác của góc AIE nên IO’ cũng là đường cao của tam giác AIE
Suy ra: IO’ ⊥ AE hay
Tứ giác AMIN có ba góc vuông nên nó là hình chữ nhật.
Câu 28:
b) Chứng minh IM . IO = IN . IO’
 Xem đáp án
Xem đáp án
b) Tam giác AIO vuông tại A có AM ⊥ IO
Theo hệ thức lượng trong tam giác vuông, ta có: IA2 = IM.IO (1)
Tam giác AIO’ vuông tại A có AN ⊥ IO’
Theo hệ thức lượng trong tam giác vuông, ta có: IA2 = IN.IO’ (2)
Từ (1) và (2) suy ra: IM.IO = IN.IO’
Câu 29:
c) Chứng minh rằng OO’ là tiếp tuyến của đường tròn có đường kính là DE
 Xem đáp án
Xem đáp án
c) Ta có: IA = ID = IE (chứng minh trên)
Suy ra A nằm trên đường tròn tâm I đường kính DE
Vì OO’ ⊥ IA tại A nên OO’ là tiếp tuyến của đường tròn tâm I, đường kính DE.
Câu 30:
d) Tính độ dài DE, biết rằng OA = 5 cm, O’A = 3,2 cm.
 Xem đáp án
Xem đáp án
d) Tam giác O’IO vuông tại I có IA ⊥ OO’
Theo hệ thức lượng trong tam giác vuông, ta có:
IA2 = OA.O’A = 5.3,2 = 16
Suy ra: IA = 4 (cm). Mà DE = 2IA nên DE = 2 . 4 = 8 (cm).
Câu 31:
Cho S = 1 + 3 + 32 + … + 330. Tìm chữ số tận cùng của S. Từ đó, suy ra S không phải là số chính phương.
 Xem đáp án
Xem đáp án
Ta có S = 1 + 3 + 32 + … + 330
= (1 + 3 + 32 + 33) + (34 + 35 + 36 + 37) +…+ (324 + 325 + 326 + 327) + 328 + 329+ 330
= (1 + 3 + 32 + 33) + 34.(1 + 3 + 32 + 33) +…+ 324.(1 + 3 + 32 + 33) + 328 + 329 + 330
= 40 + 34 . 40+…+ 324 . 40 + 328 + 329 + 330
= 40 . (1 + 34 + … + 324) + 328 + 329 + 330
= 4 . 10 . (1 + 34 + … + 324) + 328 + 329 + 330
Nhận thấy 4 . 10 . (1 + 34 + … + 324) có chữ số tận cùng là 0.
• 328 = 34.7 = …1
• 329 = 328.3 = …1 × 3 = …3
• 330 = 328.32 = …1 × 9 = …9
Tổng S có tận cùng là: 0 + 1 + 3 + 9 = …3.
Vì số chính phương không có tận cùng là 3 nên S không là số chính phương.
Câu 32:
Cho tam giác ABC có diện tích 360 cm2. Trên AB lấy điểm M sao cho AM = 2MB. Trên cạnh AC lấy điểm N sao cho AN = 2NC. Nối M với N. Tính diện tích tam giác AMN.
 Xem đáp án
Xem đáp án
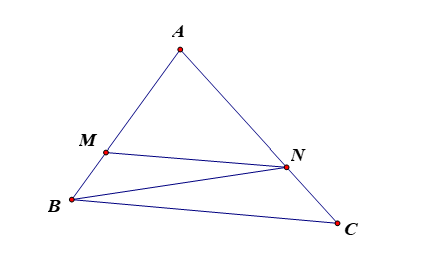
Nối B với N.
Vì AM = 2MB nên ; AN = 2NC nên
Ta có
= 240 (cm2).
Do đó = 160 (cm2).
Vậy diện tích tam giác AMN là 160 cm2.
Câu 33:
Người ta trồng lúa trên một thửa ruộng hình chữ nhật có chiều rộng là 35m, chiều dài bằng chiều rộng. Cứ trung bình 1m2 thửa ruộng đó thu hoạch được 20kg thóc. Hỏi cả thửa ruộng trên thu hoạch được bao nhiêu tấn thóc?
 Xem đáp án
Xem đáp án
Chiều dài của thửa ruộng hình chữ nhật đó là:
(m)
Diện tích của thửa ruộng hình chữ nhật đó là:
49 × 35 = 1 715 (m2)
Số tấn thóc thu hoạch được trên thửa ruộng đó là:
1 715 × 20 = 34 300 (kg)
Đổi: 343 00 kg = 34,3 tấn thóc.
Đáp số: 34,3 tấn thóc.
Câu 34:
Cho n ∈ ℤ, chứng minh A = n4 – 4n3 – 4n2 + 16n chia hết cho 384 với mọi n chẵn.
 Xem đáp án
Xem đáp án
A = n4 – 4n3 – 4n2 + 16n
A = n(n3 – 4n2 – 4n + 16)
A = n(n – 4)(n2 – 4) (1)
Vì n là số chẵn nên n = 2k (k là số nguyên dương) thay vào (1), ta được:
A = 2k(2k – 4)(4k2 – 4)
A = 16k(k – 2)(k – 1)(k + 1)
A = 16(k – 2)(k – 1)k(k + 1) (2)
Do (k – 2)(k – 1)k(k + 1) là tích của 4 số nguyên liên tiếp nên tích này luôn chia hết cho 3 và 8, mà ƯC(3, 8) = 1 nên (k – 2)(k – 1)k(k + 1) chia hết cho 24 (3)
Từ (2) và (3), suy ra A = n4 – 4n3 – 4n2 + 16n chia hết cho 384.
Câu 35:
Chứng minh rằng phân số là phân số tối giản.
 Xem đáp án
Xem đáp án
Gọi d = ƯCLN(3n – 2, 4n – 3), (d ∈ ℕ)
Khi đó 3n – 2 ⋮ d ⇒ 4(3n – 2) ⋮ d ⇒12n – 8 ⋮ d
Và 4n – 3 ⋮ d ⇒ 3(4n – 3) ⋮ d ⇒ 12n – 9 ⋮ d
Do đó (12n – 8) − (12n – 9) ⋮ d ⇒ 1 ⋮ d hay d = 1.
Do đó ƯCLN(3n – 2, 4n – 3) = 1.
Vậy phân số là phân số tối giản.
Câu 36:
Lúc 8 giờ sáng, một người đi xe máy từ A với vận tốc 45 km/giờ về phía B. Cùng thời điểm đó, tại điểm C (trên đường từ A đến B) cách A 20 km, một người đi xe đạp với vận tốc 15 km/giờ cũng đi về phía B. Hỏi lúc mấy giờ thì hai xe gặp nhau?
 Xem đáp án
Xem đáp án
Hiệu vận tốc hai xe là: 45 – 15 = 30 (km/giờ)
Thời gian để hai xe gặp nhau là:
20 : 30 = (giờ) = 40 (phút)
Hai xe gặp nhau lúc:
8 giờ + 40 phút = 8 giờ 40 phút.
Đáp số: 8 giờ 40 phút.
Câu 37:
 Xem đáp án
Xem đáp án
Nửa chu vi của mảnh vườn hình chữ nhật đó là:
96 : 2 = 48 (m)
Ta có sơ đồ:

Chiều rộng của mảnh vườn hình chữ nhật đó là:
48 : (5 + 7) × 5 = 20 (m)
Chiều dài của mảnh đất hình chữ nhật đó là:
48 – 20 = 28 (m)
Diện tích của mảnh đất hình chữ nhật đó là:
20 × 28 = 560 (m2)
Đáp số: 560 m2.
Câu 38:
Một người đi xe đạp, trong 3 giờ đầu mỗi giờ đi được 10,8 km, trong 4 giờ tiếp theo mỗi giờ đi được 9,52 km. Hỏi người đó đi được bao nhiêu ki-lô-mét?
 Xem đáp án
Xem đáp án
Trong 3 giờ đầu người đó đi được:
10,8 × 3 = 32,4 (km)
Trong 4 giờ tiếp người đó đi được:
9,52 x 4 = 38,08 (km)
Người đó đã đi được tất cả:
32,4 + 38,08 = 70,48 (km)
Đáp số: 70,48 (km).
Câu 39:
Tổng của hai số là 780. Biết số bé là số có hai chữ số và khi viết thêm chữ số 6 vào bên trái số bé thì ta được số lớn. Tìm hai số đó.
 Xem đáp án
Xem đáp án
Vì viêt số 6 vào bên trái số bé thì ta được số lớn nên số lớn hơn số bé 600 đơn vị.
Do đó, số lớn là: (780 + 600) : 2 = 690.
Số bé là: 690 – 600= 90
Đáp số: Số lớn: 690;
Số bé : 90.
Câu 40:
Trung bình cộng của ba số là 120. Hỏi cần thêm vào số nào để trung bình cộng của các số nhận được là 110?
 Xem đáp án
Xem đáp án
Tổng của ba số là: 120 × 3 = 360
Tổng của bốn số là: 110 × 4 = 440
Số cần thêm là: 440 – 360 = 80.
Đáp số: 80.
Câu 41:
Tìm ba số có trung bình cộng bằng 120, biết rằng nếu viết thêm chữ số 0 vào bên phải số thứ nhất thì được số thứ hai và số thứ ba gấp 4 lần số thứ nhất?
 Xem đáp án
Xem đáp án
Tổng của ba số là: 120 × 3 = 360
Nếu viết thêm chữ số 0 vào bên phải số thứ nhất thì được số thứ hai, vậy số thứ hai gấp 10 lần số thứ nhất
ta có sơ đồ:

Tổng số phần bằng nhau là:
1 + 10 + 4 = 15 (phần)
Số thứ nhất là:
360 : 15 × 1 = 24
Số thứ hai là:
24 × 10 = 240
Số thứ ba là:
360 − (24 + 240) = 96
Đáp số: Số thứ nhất: 24
Số thứ hai: 240
Câu 42:
Tìm 7 số tự nhiên liên tiếp biết trung bình cộng của chúng bằng số lẻ bé nhất có 2 chữ số?
 Xem đáp án
Xem đáp án
Số lẻ bé nhất có hai chữ số là 11.
Vì trung bình cộng của chúng là số hạng ở giữa. Do đó số hạng thứ 4 là 11.
Vậy 7 số liên tiếp đó là 8; 9; 10; 11; 12; 13; 14.
Câu 43:
Tìm hai số chẵn biết rằng tổng của chúng là 40 đơn vị và giữa hai số đó có đúng một số chẵn?
 Xem đáp án
Xem đáp án
Vì giữa hai số đó có đúng một số chẵn nên hiệu của hai số chẵn đó là 2 đơn vị.
Số chẵn lớn là: (40 + 2) : 2 = 22
Số chẵn bé là: 40 – 22 = 18
Đáp số: 18 và 22.
Câu 44:
 Xem đáp án
Xem đáp án
Vì với mọi x và (3y + 10)2008 ≥ 0 với mọi y
Nên
Để thì
.
Vậy là giá trị cần tìm.
Câu 45:
 Xem đáp án
Xem đáp án
Mỗi năm mỗi người tăng thêm 1 tuổi
Tổng số tuổi của hai ông cháu hiện nay là:
81 – 3 – 3 = 75 (tuổi)
Tuổi của cháu hiện nay là: (75 – 59) : 2 = 8 (tuổi)
Tuổi của ông hiện nay là: 8 + 59 = 67 (tuổi)
Đáp số: Tuổi cháu: 8 tuổi
Tuổi ông: 67 tuổi.
Câu 46:
Để lát nền một căn phòng hình chữ nhật, người ta dùng loại gạch men hình vuông có cạnh 30 cm. Hỏi cần bao nhiêu viên gạch để lát kín nền căn phòng đó, biết rằng căn phòng có chiểu rộng 6 m, chiều dài 9 m? (Diện tích phần mạch vữa không đáng kể)
 Xem đáp án
Xem đáp án
Diện tích nền căn phòng là:
9 × 6 = 54 (m2)
Đổi: 54 m2 = 5 400 dm2; 30 cm = 3 dm
Diện tích một viên gạch là:
3 × 3 = 9 (dm2)
Số viên gạch cần dùng là:
5 400 : 9 = 600 (viên)
Đáp số: 600 viên gạch.
Câu 47:
 Xem đáp án
Xem đáp án
Vì (2x – 5)2020 ≥ 0, ∀x và (3y + 4)2022 ≥ 0, ∀y
Nên (2x – 5)2020 + (3y + 4)2022 ≥ 0, ∀x, y.
Do đó để (2x – 5)2020 + (3y + 4)2022 ≤ 0 thì
Vậy .
Câu 48:
 Xem đáp án
Xem đáp án
Ta có a2(b + c) = b2(c + a)
(a2b – b2a) + (a2c – b2c) = 0
ab(a – b) + c(a – b)(a + b) = 0
(a – b)(ab + bc + ac) = 0
ab + bc + ac = 0 (vì a ≠ b).
Lại có a2(b + c) = b2(c + a)
⇒ a2 = (a + c)(a + b)
Do đó 2012 = a2(b + c) = (a + b)(a + c)(b + c) = (a + b)(ab + bc + ac + c2).
Vì ab + bc + ac = 0 nên c2(a + b) = 2012.
Vậy M = c2(a + b) = 2012.
Câu 49:
Phân tích đa thức 4a2 – 4b2 – 4a + 1 thành nhân tử.
 Xem đáp án
Xem đáp án
4a2 – 4b2 – 4a + 1
= (4a2 – 4a + 1) – 4b2
= (2a − 1)2 – 4b2
= (2a – 2b −1)(2a + 2b −1)
Câu 50:
Tính:
a) 300 + 5 + 0,14;
b) 45 + 0,9 + 0,008;
 Xem đáp án
Xem đáp án
a) 300 + 5 + 0,14 = 305 + 0,14 = 305,14.
b) 45 + 0,9 + 0,008 = 45,9 + 0,008 = 45,908.
Câu 51:
Điền vào chỗ chấm
a) 5 tấn 8 tạ = …. kg
b) 8 tấn 5 tạ = …. kg
 Xem đáp án
Xem đáp án
a) 5 tấn 8 tạ = 5 800 kg.
b) 8 tấn 5 tạ = 8 500 kg.
Câu 52:
Tìm số tự nhiên x lớn nhất biết: x < 3,005.
 Xem đáp án
Xem đáp án
Vì x < 3,005 ⇒ x ∈ {0; 1; 2; 3}
Mà x là số tự nhiên lớn nhất nên x = 3.
Câu 53:
Tìm số x tự nhiên lớn nhất biết 75 ⋮ x và 105 ⋮ x.
 Xem đáp án
Xem đáp án
Vì 75 ⋮ x và 105 ⋮ x nên x ∈ ƯC(75, 105)
Mà x là số tự nhiên lớn nhất nên x là ƯCLN(75, 105)
Có 75 = 3 . 52; 105 = 3 . 5 . 7
⇒ x = ƯCLN(75, 105) = 3.5 = 15.
Vậy x = 15.
Câu 54:
Giá gạo tháng 3 cao hơn tháng 2 là 20%. Giá gạo tháng 4 thấp hơn tháng 3 là 10%. Hỏi giá gạo tháng 4 so với tháng 2 cao hơn hay thấp hơn bao nhiêu %?
 Xem đáp án
Xem đáp án
Coi giá gạo tháng 2 là 100% thì giá gạo tháng 3 so với tháng 2 là:
100% + 20% = 120%
Coi giá gạo tháng 3 là 100% thì giá gạo tháng 4 so với giá gạo tháng 3 là:
100% − 10% = 90%
Giá tháng 4 so với giá gạo tháng 2 là:
120% × 90% = 108%
Vậy giá gạo tháng 4 đắt hơn giá gạo tháng 2 là:
108% − 100% = 8%.
Đáp số: giá gạo tháng 4 cao hơn 8% so với giá gạo tháng 2.
Câu 55:
 Xem đáp án
Xem đáp án
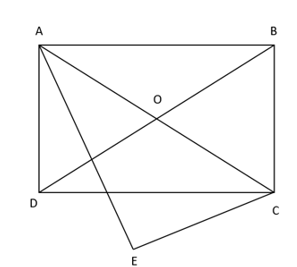
Vì ABCD là hình chữ nhật nên nội tiếp đường tròn
Xét tứ giác ADEC có
Do đó tứ giác ADEC nội tiếp
Vậy 5 điểm A, B, C, D, E cung thuộc đường tròn .
Câu 56:
Cho đường tròn tâm O có đường kính AB = 2R. Từ trung điểm H của đoạn OB kẻ đường thẳng vuông góc với AB cắt đường tròn (O) tại C và D.
a) Chứng minh HC = HD và tứ giác ODBC là hình thoi
 Xem đáp án
Xem đáp án
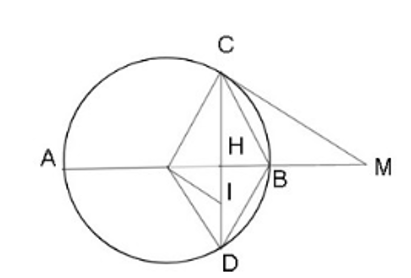
a) Xét (O) có OB vuông góc với CD nên H là trung điểm của CD.
Do đó HC = HD.
Xét tứ giác ODBC có H là trung điểm của OB và CD nên tứ giác ODBC là hình bình hành.
Mà OC = OD (gt) nên tứ giác ODBC là hình thoi.
Câu 57:
b) Tính số đo góc BOC
 Xem đáp án
Xem đáp án
b) Vì tứ giác ODBC là hình thoi nên OC = BC.
Mà OC = OB (= R) nên OC = OB = BC.
Do đó tam giác OBC là tam giác đều.
Suy ra .
Câu 58:
c) Gọi M là điểm đối xứng của O qua B. Chứng minh MC là tiếp tuyến tại C của đường tròn (O). Tính MC theo R.
 Xem đáp án
Xem đáp án
c) Có OB = BC (chứng minh trên).
Mà OB = BM. Do đó OB = BC = BM.
Suy ra tam giác OCM vuông tại C. Do đó .
Do đó MC là tiếp tuyến của (O).
Xét tam giác OCM vuông tại C
Áp dụng định lý Py-ta-go, ta có:
OM2 = OC2 + CM2 hay 4R2 = R2 + MC2.
Suy ra MC2 = 4R2 – R2 = 3R2.
Do đó .
Câu 59:
d) Qua O kẻ đường thẳng vuông góc với OC cắt CD ở I. Chứng minh HI.HD + HB.HM = R2
 Xem đáp án
Xem đáp án
d) Vì ODBC là hình thoi nên OB là đường phân giác của góc COD
Suy ra
Mà hay
Mà .
Suy ra .
Xét tam giác HOI và tam giác HDO có:
là góc chung,
(chứng minh trên)
Do đó tam giác HOI đồng dạng với tam giác HDO (g.g)
Suy ra ⇒ HI . HD = OH2.
Chứng minh tương tự, ta có: HB . HM = HC2.
Mà OH2 + HC2 = OC2 (do tam giác OCH vuông tại H).
Do đó HI . HD + HB . HM = OH2 + HC2 = OC2 = R2.
Câu 60:
Có 9 can nước mắm như nhau đựng tất cả 6,75 lít nước mắm. Hỏi 6 can nước mắm như thế đựng bao nhiêu lít nước mắm?
 Xem đáp án
Xem đáp án
Một can nước mắm đựng được số lít là:
6,75 : 9 = 0,75 (lít)
6 can nước mắm có số lít là:
0,75 × 6 = 4,5 (lít)
Đáp số: 4,5 lít.
