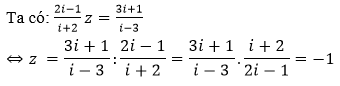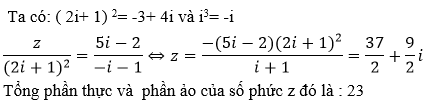30 câu hỏi trắc nghiệm thuộc 125 câu trắc nghiệm Số phức cơ bản-P2 (có đáp án)

Câu 1:

Cho số phức z = ( 3 - 2i)(1 + i) ² . Môđun của $w = i z + \bar{z}$ là

A.2.

B. $2 \sqrt{2}$

C. 1.

D. $\sqrt{2}$

Xem đáp án

Chọn B.

Câu 2:

Cho số phức z thỏa mãn điều kiện $(2 + i) z + \frac{1 - i}{1 + i} = 5 - i$ . Môđun của số phức W = 1 + 2z + z² có giá trị là:

A. 10.

B. -10.

C. 100.

D. -100.

Xem đáp án

Chọn A.

Câu 3:

Cho số phức z = -3 + 2i. Tính P = |z + 1 – i|.

A. P = 4.

B. P = 1.

C. $P = \sqrt{5}$

D. $P = 2 \sqrt{2}$

Xem đáp án

Chọn C.

Ta có: z + 1 - i = -3 + 2i + 1 - i = -2 + i

Câu 4:

Cho hai số phức z₁= 3 - 2i; z₂= -2 + i Tính P = | z₁ + z₂|.

A. P = 2.

B. $P = \sqrt{2}$

C. P = 1/2.

D. P = 2.

Xem đáp án

Chọn B.

Ta có: z₁+ z₂= (3 - 2i) + (-2 + i) = 1 - i

Câu 5:

Cho hai số phức z₁= 3 + i; z₂= 2 - i. Tính P = | z₁ + z₁ z₂|.

A. P = 10.

B. P = 50.

C. P = 5.

D. P = 85.

Xem đáp án

Chọn A.

Ta có

+) z₁z₂= (3 + i) (2 - i) = 6 - 3i + 2i - i²= 7 - i

+) z₁+ z₁z₂= (3 + i) + (7 - i) = 10

Vậy P = | z₁ + z₁ z₂| = 10

Câu 6:

Cho số phức z thỏa mãn điều kiện: $(1 + i) \bar{z} - 1 - 3 i = 0$ . Phần ảo của số phức w = 1 - iz + z là

A. 1.

B. -3.

C. -2.

D. -1.

Xem đáp án

Chọn B.

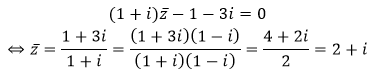
Vậy z = 2 - i và w = 1- iz + z = 1 - i( 2 - i) + 2 - i = 2 - 3i

Phần ảo của w là -3.

Câu 7:

Tìm phần thực, phần ảo của số phức z thỏa ( $\frac{z}{2}$ – i)(1 - i) = ( 1 + i) ³⁹⁷⁹

A. Phần thực là 2¹⁹⁹⁰ và phần ảo là 2.

B. Phần thực là - 2¹⁹⁹⁰ và phần ảo là 2.

C. Phần thực là -2¹⁹⁸⁹ và phần ảo là 1.

D. Phần thực là 2¹⁹⁸⁹ và phần ảo là 1.

Xem đáp án

Chọn B.

Ta có:

Vậy phần thực và phần ảo của số phức z là $- 2^{1990} v à 2 .$

Câu 8:

Cho số phức z thỏa z = 1+ i+ i²+ i³+...+ i²⁰¹⁶. Khi đó phần thực và phần ảo của z lần lượt là

A. 0 và -1.

B. 0 và 1.

C. 1 và 1.

D. 1 và 0.

Xem đáp án

Chọn D.

Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = i .

Do đó :

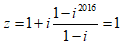
Vậy phần thực và phần ảo của z là 1 và 0.

Câu 9:

Giá trị của biểu thức S = 1+ i²+ i⁴+ ...+ i^4k là

A. 1.

B. 0.

C. 2.

D. ik.

Xem đáp án

Chọn A.

Ta có nhận xét sau:

i²ⁿ+ i^{2n+ 2}= i²ⁿ(1 + i²) = 0 .

Áp dụng tính được

S = 1+ (i²+ i⁴) + ( i⁶+ i⁸) + ...+ ( i^4k-2+ i^4k) = 1 + 0 + 0 + 0 + ... + 0 = 1.

Câu 10:

Cho số phức z = 1+ ( 1+ i) + ( 1+i) ²+ ...+ (1+ i) ²⁶ . Phần thực của số phức z là

A. $2^{13}$

B. $- (1 + 2^{13})$

C. $- 2^{13}$

D. $1 + 2^{13}$

Xem đáp án

Chọn A. Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = 1 + i. Do đó:

Vậy phần thực là: 2¹³

Câu 11:

Cho số phức z = x + y.i thỏa mãn z³ = 2 - 2i. Cặp số là(x;y)

A. (2; 2).

B. (-1; -1).

C. (3;-3).

D. (2; -3).

Xem đáp án

Chọn B.

Giải phương trình trên suy ra x = y = -1

Vậy (x; y) = (-1; -1).

Câu 12:

Cho số phức z = 3 + i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:

A. $M (\frac{3}{10}; - \frac{1}{10})$

B.

C.

D.

Xem đáp án

Chọn A

Câu 13:

Gọi A là điểm biểu diễn của số phức z = 3 + 2i và B là điểm biểu diễn của số phức w = 2 + 3i. Trong các khẳng định sau, khẳng định nào đúng?

A. Hai điểm A và B đối xứng nhau qua trục tung.

B. Hai điểm A và B đối xứng nhau qua gốc tọa độ O.

C. Hai điểm A và B đối xứng nhau qua đường thẳng y = x.

D. Hai điểm A và B đối xứng nhau qua trục hoành.

Xem đáp án

Chọn C.

Tọa độ điểm A và B lần lượt là: A(3;2) và B(2;3). Suy ra $\vec{A B} (- 1; 1)$

Đường thẳng y = x hay x - y = 0 có vecto pháp tuyến là $\vec{n} (1; - 1)$

Do 2 vecto $\vec{n}; \vec{A B}$ là 2 vecto cùng phương nên đường thẳng AB vuông góc với đường thẳng y = x.

Gọi M(5/2; 5/2) là trung điểm AB; ta thấy M thuộc đường thẳng y = x. Do đó đường thẳng y = x là đường trung trực của AB.

Hay A và B đối xứng nhau qua y = x.

Câu 14:

Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:

A. $2 \sqrt{5}$

B. $\sqrt{13}$

C. $2 \sqrt{10}$

D. $2 \sqrt{2}$

Xem đáp án

Chọn C.

Ta có: iz + 2 - i = 0 $\Leftrightarrow$ iz = i - 2 $\Leftrightarrow z = \frac{i - 2}{i} = \frac{(i - 2) (- i)}{1} = 1 + 2 i$

Điểm biểu diễn của số phức z là A(1; 2)

Do đó: AM = $\sqrt{{(3 - 1)}^{2} + {(- 4 - 2)}^{2}} = \sqrt{40} = 2 \sqrt{10}$

Câu 15:

Tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z – (1+ i)| = |z + 2i| là đường nào sau đây?

A. Đường thẳng.

B. Đường tròn.

C. Elip.

D. Parabol.

Xem đáp án

Chọn A.

Câu 16:

Tìm tập hợp những điểm M biểu diễn số phức z trong mặt phẳng phức, biết số phức z thỏa mãn điều kiện $|z - 2 i| = |\bar{z} + 1|$

A. Tập hợp những điểm Mlà đường thẳng có phương trình 4x + 2y + 3 = 0.

B. Tập hợp những điểm M là đường thẳng có phương trình 4x - 2y + 3 = 0.

C. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y - 3 = 0.

D. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y + 3 = 0.

Xem đáp án

Chọn C.

Câu 17:

Tập hợp các điểm M biểu diễn số phức z thoả mãn |z – 2 + 5i| = 4 là:

A. Đường tròn tâm I(2 ; -5) và bán kính bằng 2.

B. Đường tròn tâm I(-2 ; 5) và bán kính bằng 4.

C. Đường tròn tâm I(2 ; -5) và bán kính bằng 4.

D. Đường tròn tâm O và bán kính bằng 2.

Xem đáp án

Chọn C.

Câu 18:

Cho z là số phức thỏa mãn $\frac{z + 1}{z - 1}$ là số thuần ảo. Tìm khẳng định đúng

A. $|z| = \sqrt{5}$

B. |z| = 1

C. |z| = 2

D. $|z| = \sqrt{2}$

Xem đáp án

Chọn B.

Ta có:

$\frac{z + 1}{z - 1}$ là số thuần ảo

$\Leftrightarrow \frac{z + 1}{z - 1} = - \bar{\frac{z + 1}{z - 1}} \Leftrightarrow \frac{z + 1}{z - 1} + \bar{\frac{z + 1}{z - 1}} = 0$

$\Leftrightarrow \frac{z + 1}{z - 1} + \frac{\bar{z + 1}}{\bar{z - 1}} = 0$

Vậy |z| = 1.

Câu 19:

Cho số phức z thỏa mãn $\frac{2 z + 1}{z - 2}$ là số thực. Khẳng định nào sau đây sai

A. z là số thực.

B. z là số ảo.

C. |z| = z.

D. $\bar{z} = z$

Xem đáp án

Chọn B.

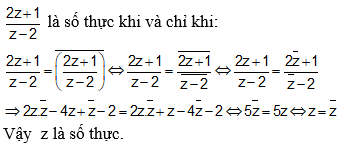
Từ đó z = |z|

Câu 20:

Cho các số thực a; b; c và d thỏa mãn: a+ bi= ( c+ di) ⁿ. Tìm khẳng định đúng

A. a²+ b²= 2( c²+ d²) ⁿ

B. a²+ b²= c²+ d²

C. a²+ b²= 2ⁿ( c²+ d²)

D. a²+ b²= ( c²+ d²)ⁿ

Xem đáp án

Chọn D.

Câu 21:

Tính tổng modul của các số phức z thỏa mãn z²+ |z| = 0

A. 1.

B. 2.

C. 3.

D. 4.

Xem đáp án

Chọn B.

Câu 22:

Có bao nhiêu số phức z thỏa mãn: $z^{2} + \bar{z} = 0$

A. 1.

B. 2.

C. 3.

D. 4.

Xem đáp án

Chọn D.

Câu 23:

Có bao nhiêu số phức z thỏa mãn: z²+ |z| = $\bar{z}$ .

A. 1.

B. 2.

C. 3.

D. 4.

Xem đáp án

Chọn C.

Câu 24:

Tìm các số phức z thỏa mãn: $z^{3} - \bar{z} = 0$

A. z = 0

B. $z = \pm 1$

C. $z = \pm i$

D. Tất cả đúng.

Xem đáp án

Chọn D.

Câu 25:

Tìm phần thực của số phức z thỏa mãn $\frac{z}{\bar{z}} + z = 2$

A. 0.

B. 1.

C. 3.

D. 4.

Xem đáp án

Chọn B.

Câu 26:

Giải phương trình sau đây (2 + i)z = z + 2i - 1

A. z = 1 + i.

B. z = $\frac{1}{2}$ + $\frac{3}{2}$ i.

C. z = 2+ i.

D. Đáp án khác.

Xem đáp án

Chọn B.

Câu 27:

Tìm tổng phần thực và phần ảo của số phức z thỏa mãn: (1 - i) ( z - 2i) = 2 + i.

A. 4.

B. 3.

C. 5.

D. 7.

Xem đáp án

Chọn A.

Câu 28:

Giải phương trình sau đây : $\frac{2 i - 1}{i + 2} z = \frac{3 i + 1}{i - 3}$

A. z = 2.

B. z = -1.

C. z = -i.

D. z = 2i.

Xem đáp án

Chọn B.

Câu 29:

Tính tổng phần thực và phần ảo cùa số phức z thỏa mãn điều kiện sau: $\frac{z}{{(2 i + 1)}^{2}} = \frac{5 i - 2}{2 i^{3} + i - 1}$

A. 15.

B. 20.

C. 23.

D. 27.

Xem đáp án

Chọn C.

Câu 30:

Phần thực của số z thỏa mãn phương trình: (5 - 4i) z = ( 3 + 2i)(4 - i) gần với giá trị nào nhất.

A. 1,21.

B. 1,22.

C. 1,23.

D. 1,24.

Xem đáp án

Chọn B.

Ta có: (5 - 4i) z = ( 3 + 2i)(4 - i)

Suy ra: (5 - 4i)z = 14 + 5i

$\Leftrightarrow z = \frac{14 + 5 i}{5 - 4 i}$

$\Leftrightarrow z = \frac{(14 + 5 i) (5 + 4 i)}{41}$

$\Leftrightarrow z = \frac{50}{41} + \frac{81}{40} i$

Lại có: $\frac{50}{41} \approx 1, 22$

CHỌN BỘ SÁCH BẠN MUỐN XEM

125 câu trắc nghiệm Số phức cơ bản (có đáp án)

125 câu trắc nghiệm Số phức cơ bản-P2 (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương