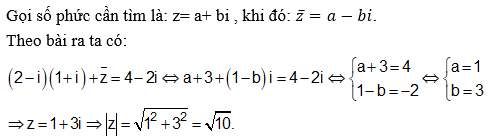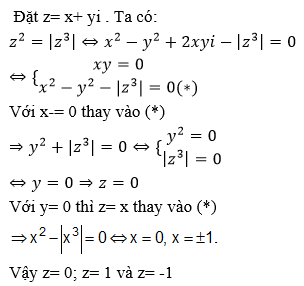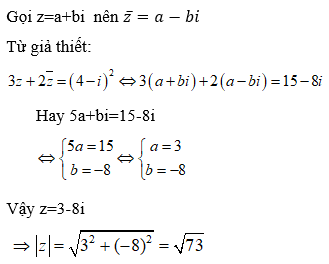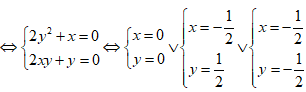25 câu hỏi trắc nghiệm thuộc 125 câu trắc nghiệm Số phức cơ bản-P3 (có đáp án)

Câu 1:

Phần ảo của số z thỏa mãn phương trình: ( z + 2)i = ( 3i - z)( -1 + 3i) gần với giá trị nào nhất.

A. 2,11.

B. 2,21.

C. 2,31.

D. 2,41.

Xem đáp án

Chọn D.

Ta có: (z + 2)i = (3i - z)( -1 + 3i)

Suy ra: iz + 2i = -3i + 9i²+ z - 3iz

(-1 + 4i) z = - 9 - 5i

$\Rightarrow z = \frac{- 9 - 5 i}{- 1 + 4 i} = \frac{- (9 + 5 i) (- 1 - 4 i)}{17} = \frac{- 11}{17} + \frac{41}{17} i$

Ta có: $\frac{41}{17} \approx 2, 41$

Câu 2:

Cho phương trình sau: $(2 i z - 3) (z - 5 i) (\bar{z} - 3 + 6 i) = 0$ .Tính tổng tất cả các phần thực của các nghiệm của phương trình.

A. 2

B. 3

C. 4

D. 5

Xem đáp án

Chọn B.

Ta có:

Vậy nghiệm của phương trình là: z = $- \frac{3}{2}$ i ; z = 5i và z = 3 + 6i

Tổng các phần thực của các nghiệm trên là 3.

Câu 3:

Cho số phức z thỏa mãn ( 3+ i) z = 2. Tính mô-đun của số phức w = z + $\frac{2}{5}$ - $\frac{4}{5}$ i.

A. 1.

B. 2.

C. $\sqrt{2}$

D. $\sqrt{3}$

Xem đáp án

Chọn C.

Đặt z = a+ bi.

Theo đề ra ta có: ( 3 + i) z = 2

Hay ( 3 + i)( a + bi) = 2

Suy ra: 3a - b + ( 3b + a) i = 2

$\Leftrightarrow \{\begin{array}{l} 3 a - b = 2 \\ a + 3 b = 0 \end{array} \Leftrightarrow \{\begin{cases} a = \frac{3}{5} \\ b = \frac{- 1}{5} \end{cases}$

nên z = $\frac{3}{5}$ - $\frac{1}{5}$ i.

Khi đó w = $\frac{3}{5}$ - $\frac{1}{5}$ i + $\frac{2}{5}$ - $\frac{4}{5}$ i = 1 - i.

Vậy $|w| = \sqrt{1^{2} + 1^{2}} = \sqrt{2}$ .

Câu 4:

Cho số phức z thỏa mãn điều kiện $(2 + i) z + \frac{1 - i}{1 + i} = 5 - i$ . Tìm phần thực của số phức w = 4z

A. 7.

B. 8.

C. 10.

D. 11.

Xem đáp án

Chọn B.

$(2 + i) z + \frac{1 - i}{1 + i} = 5 - i \Leftrightarrow (2 + i) z + \frac{(1 - i) (1 - i)}{(1 - i) (1 + i)} = 5 - i \Leftrightarrow (2 + i) z - i = 5 - i$

$\Leftrightarrow (2 + i) z = 5 \Leftrightarrow z = \frac{5}{2 + i} = 2 - i$

Khi đó w = 4z = 4(2 - i) = 8 - 4i

Câu 5:

Cho số phức z thỏa mãn hệ thức: $(2 - i) (1 + i) + \bar{z} = 4 - 2 i$ . Tính mô-đun của z.

A. 3.

B. 4.

C. $\sqrt{8}$

D. $\sqrt{10}$

Xem đáp án

Chọn D

Câu 6:

Tìm nghiệm của phương trình $\frac{2 z - 1}{z + i} = 1 + i$

A.

C.

B.

D.

Xem đáp án

Chọn D.

Điều kiện: z ≠ - i.

Với điều kiện trên, phương trình đã cho trở thành:

2z- 1= ( 1+ i) ( z+ i)

Hay 2z - 1 = (1 + i) z + i + i²

Suy ra: ( 2 - 1 - i) z = i - 1 + 1.

Hay (1 - i) z = i

Vậy z cần tìm là:

Câu 7:

Tìm nghiệm của phương trình $\frac{i}{z} = \frac{1}{2 - i} + \frac{1}{3 + 6 i}$

A.

B.

C.

D.

Xem đáp án

Chọn C.

Điều kiện: z ≠ 0

Với điều kiện trên, phương trình đã cho trở thành:

Câu 8:

Tìm nghiệm của phương trình: $[(1 + 2 i) \bar{z} + 2 - i] (i z + \frac{1}{i}) = 0$

A. z = 1; z = i.

B. z = -1; z = i.

C. z = -i; z = 1.

D. z = -1; z = -i

Xem đáp án

Chọn C.

Ta có:

Giải (1): i²z + 1 = 0 hay – z + 1 = 0

Suy ra z = 1

Giải (2):

Vậy phương trình có 2 nghiệm là z = 1 và z = -i.

Câu 9:

Tìm nghiệm của phương trình $\frac{7 + i}{{(2 i - 1)}^{3}} = \frac{3 + i}{2 z + 1}$

A. z = 1

B. z = i

C. z = -i

D. z = 2

Xem đáp án

Chọn D.

$Đ i ề u k i ệ n : z \neq - \frac{1}{2} . T a c ó : {(2 i - 1)}^{3} = 11 - 2 i \frac{7 + i}{{(2 i - 1)}^{3}} = \frac{3 + i}{2 z + 1} \Leftrightarrow (7 + i) (2 z + 1) = {(2 i - 1)}^{3} (3 + i) \Leftrightarrow 2 z + 1 = \frac{{(2 i - 1)}^{3} (3 + i)}{7 + i} = \frac{(11 - 2 i) (3 + i)}{7 + i} = 5 \Leftrightarrow z = 2$

Câu 10:

Tìm nghiệm của phương trình $\frac{2 + i - z}{{(3 - i)}^{2}} = \frac{2 z + 1}{10 + 5 i}$

A. z = 2i

B. z = 1 + i

C. z = i

D. z = 2 + i

Xem đáp án

Chọn đáp án C.

⇔ (2 + i – z)(10 + 5i) = (2z + 1) (3 – i)²

$\Leftrightarrow$ ( 2 + i)( 10 + 5i) – ( 10 + 5i) z = 2( 3 - i)²z + (3 - i)²

Suy ra: ( 26 - 7i) z = 7 + 26i

Hay z = $\frac{7 + 26 i}{26 - 7 i}$ = i.

Câu 11:

Tính tổng các phần ảo của các số phức z thỏa mãn phương trình ${(z - 2 \bar{z})}^{3} = 8$

A. 0.

B. 1.

C. 2.

D. 4.

Xem đáp án

Chọn A.

Do đó tổng các phần ảo là $\frac{\sqrt{3}}{3} + \frac{- \sqrt{3}}{3} = 0 .$

Câu 12:

Cho số phức z thỏa mãn: $\bar{z^{2}} + 2011 = 0$ . Tìm khẳng định đúng?

A. Có 2 số phức z thỏa mãn.

B. các số phức đó là số thực.

C. Các số phức đó là số ảo.

D. Tất cả sai.

Xem đáp án

Chọn C.

Câu 13:

Có bao nhiêu số phức z thỏa mãn z²= | z³|.

A. 2.

B. 3.

C. 4.

D. 5.

Xem đáp án

Chọn B.

Câu 14:

Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)²(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?

A. -3; -2

B. 2; 3

C. 2; -3

D. Đáp án khác.

Xem đáp án

Chọn C.

Ta có: ( 1 + i)²(2 - i) z = 8 + i + (1 + 2i)z

Nên z[( 1 + i)²(2 -i) – (1 + 2i) ] = 8 + i

Suy ra: z[2i(2 - i) – 1 - 2i] = 8 + i

Vậy số phức z đã cho có phần thực là 2, phần ảo là -3.

Câu 15:

Số phức z thỏa mãn phương trình $(2 - 3 i) z + (4 + i) \bar{z} = - {(1 + 3 i)}^{2}$ có phần thực và phần ảo lần lượt là:

A: -2; 5

B. -2 và 3

C. 2 và -3

D. 3 và 5

Xem đáp án

Chọn A.

Câu 16:

Tìm phần thực của số phức $\frac{25 i}{z}$ , biết rằng $\frac{z}{2 - i} + (4 - 3 i) \bar{z} = 26 + 6 i$

A. 3.

B. -2.

C. – 4.

D. 5.

Xem đáp án

Chọn C.

Câu 17:

Có bao nhiêu số phức z thỏa |z| = 2 và z³ là số thực là:

A. 5

B. 3

C. 4

D. 6

Xem đáp án

Chọn D.

Câu 18:

Xác định tập hợp các điểm trong mặt phẳng biểu diễn số phức z thoả điều kiện |z + 1 – 3i| ≤ 4.

A. Hình tròn tâm I(-1;3), bán kính r = 4.

B. Đường tròn tâm I(-1;3), bán kính r = 4.

C. Hình tròn tâm I(-1; -3), bán kính r = 4.

D. Đường tròn tâm I(1;3), bán kính r = 4.

Xem đáp án

Chọn A.

Giả sử z = x + yi, ta có z + 1 - 3i = x + 1 + (y - 3)i.

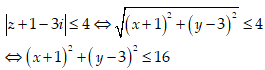
Vậy tập hợp các điểm trong mặt phẳng biểu diễn số phức z là hình tròn tâm I(-1; 3), bán kính r = 4.

Câu 19:

Giá trị của i¹⁰⁵+ i²³+ i²⁰- i³⁴ là ?

A. 2.

B. -2.

C. 4.

D. -4.

Xem đáp án

Chọn A.

Ta có: i¹⁰⁵+ i²³+ i²⁰- i³⁴= i^4.26+1+ i^{4.5+ 3}+ i^4.5- i^{4.8+ 2}= i - i + 1 + 1 = 2.

Câu 20:

Với mọi số ảo z, số z² + |z|² là :

A. Số thực âm

B. Số 0

C. Số thực dương

D. Số ảo khác 0

Xem đáp án

Chọn B.

Câu 21:

Cho số phức z thỏa mãn: $3 z + 2 \bar{z} = {(4 - i)}^{2}$ . Môđun của số phức z là

A. – 73.

B. $- \sqrt{73}$

C. 73.

D. $\sqrt{73}$

Xem đáp án

Chọn D.

Câu 22:

Tìm số phức z , biết $z - (2 + 3 i) \bar{z} = 1 - 9 i$

A.z = -2 + i.

B. z = -2 - i.

C. z = 3 + 2i.

D. z = 2 - i.

Xem đáp án

Chọn D.

Gọi z = a + bi ta có :

Từ giả thiết: $z - (2 + 3 i) \bar{z} = 1 - 9 i$

Hay ( a + bi) – (2 + 3i) ( a - bi) = 1 - 9i

Suy ra –a - 3b - ( 3a - 3b)i = 1 - 9i.

Ta có hệ phương trình: $\{\begin{cases} - a - 3 b = 1 \\ 3 a - 3 b = 9 \end{cases}$

Ta tìm được a = 2 và b = -1.

Vậy z = 2 - i.

Câu 23:

Có bao nhiêu số phức z thỏa mãn $|z| = \sqrt{2}$ và z² là số thuần ảo ?

A. 4.

B. 3.

C. 2.

D. 1.

Xem đáp án

Chọn A.

Gọi z = a + bi.

Ta có và z² = a² – b² + 2abi

Yêu cầu của bài toán thỏa mãn khi và chỉ khi

Vậy có 4 số phức thỏa mãn điều kiện bài toán.

Câu 24:

Tìm tất cả số phức z thỏa $z^{2} = {|z|}^{2} + \bar{z}$

A.

B.

C.

D.

Xem đáp án

Chọn A.

Câu 25:

Số phức z thỏa mãn: $z - (2 + 3 i) \bar{z} = 1 - 9 i$ là

A. 2 + i

B. -2 - i

C. -4 + i

D. 2 - i

Xem đáp án

Chọn D.

Gọi z = a + bi với a, b ∈ R; i² = -1

Suy ra : a + bi – (2 + 3i) (a - bi) = 1 - 9i

Hay a + bi - (2a - 2bi + 3ai + 3b) = 1 - 9i

⇔ -a – 3b + (-3a + 3b)i = 1 – 9i

CHỌN BỘ SÁCH BẠN MUỐN XEM

125 câu trắc nghiệm Số phức cơ bản (có đáp án)

125 câu trắc nghiệm Số phức cơ bản-P3 (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương