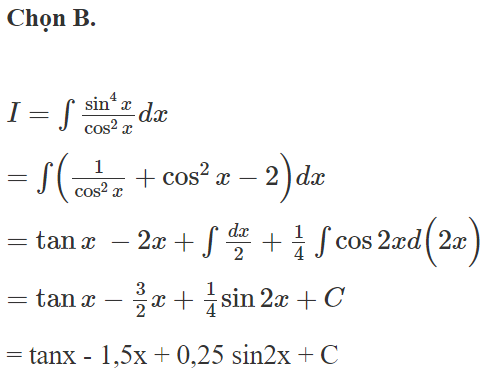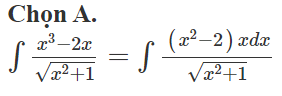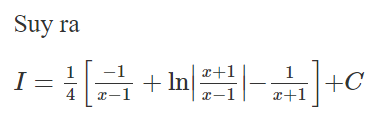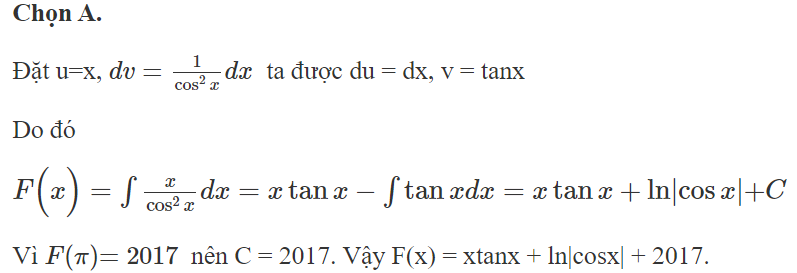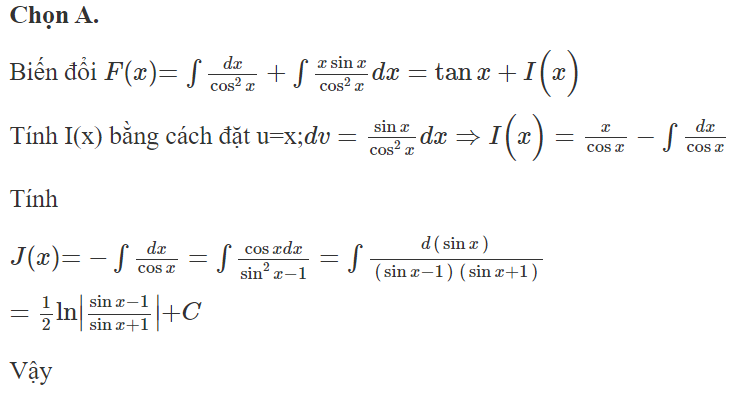30 câu hỏi trắc nghiệm thuộc 150 câu trắc nghiệm Nguyên hàm - Tích phân nâng cao-P2 (có đáp án)

Câu 1:

Tìm nguyên hàm: $I = \int \frac{\sin^{4} x}{\cos^{2} x} d x$

A. tanx - 2x + sin2x + C

B. tanx - 1,5x + 0,25 sin2x + C

C. cot2x - 0,5 x - cos2x + C

D. Đáp án khác

Xem đáp án

Câu 2:

Tìm nguyên hàm: $I = \int \cos^{4} 2 x d x$

A. 3x + sin4x + sin8x + C

B. 2x - cos2x - sin4x + C

C. $\frac{3 x}{8}$ + sin4x + sin8x + C

D. Đáp án khác

Xem đáp án

Chọn D.

Ta có:

Câu 3:

Tìm nguyên hàm: $J = \int (\cos 3 x . \cos 4 x + \sin^{3} 2 x) d x$

A. $\frac{1}{14} \sin 7 x - \frac{1}{2} \sin x - \frac{3}{8} \cos 2 x + \frac{1}{24} \cos 6 x + C$

B. $\frac{1}{14} \sin 7 x + \frac{1}{2} \sin x + \frac{3}{8} \cos 2 x + \frac{1}{24} \cos 6 x + C$

C. $\frac{1}{14} \sin 7 x + \frac{1}{2} \sin x - \frac{3}{8} \cos 2 x + \frac{1}{24} \cos 6 x + C$

D. $\frac{1}{14} \sin 7 x + \frac{1}{2} \sin x - \frac{3}{8} \cos 2 x - 2 \frac{1}{24} \cos 6 x + C$

Xem đáp án

Chọn C.

Ta có :

$\cos 3 x . \cos 4 x = \frac{1}{2} (\cos 7 x + \cos x) \sin^{3} 2 x = \frac{3}{4} \sin 2 x - \frac{1}{4} \sin 6 x$

Nên suy ra:

Câu 4:

Tìm nguyên hàm: $I = \int (\frac{1}{\ln^{2} x} - \frac{1}{\ln x}) d x$

A. $\frac{x}{\ln x} + C$

B. $\frac{x}{\ln x} + x + C$

C. x.lnx + C

D. Đáp án khác

Xem đáp án

Chọn A.

Ta có :

Câu 5:

Tìm nguyên hàm $J = \int \frac{x e^{x} + 1}{{(x + e^{x})}^{2}} d x$

A. $\frac{x + 1}{x + e^{x} + x} + C$

B. $- \frac{x + 1}{x + e^{x} + x} + C$

C. $- \frac{x + 1}{x + e^{x}} + C$

D. $\frac{x + 1}{x + e^{x}} + 2 x + C$

Xem đáp án

Chọn C.

Ta có :

Câu 6:

Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số:

A. $f (x) = \frac{\sin x + \cos x}{\sin x - \cos x}$

B. $f (x) = \frac{\sin x - \cos x}{\sin x + \cos x}$

C. $f (x) = \frac{1}{\sin x + \cos x}$

D. $f (x) = \frac{1}{|\sin x - \cos x|}$

Xem đáp án

Chọn A.

$F' (x) = \frac{(\sin x - \cos x)'}{\sin x - \cos x} = \frac{\cos x + \sin x}{\sin x - \cos x}$

Câu 7:

Kết quả tính $\int 2 x \ln (x - 1) d x$ bằng:

A. $(x^{2} - 1) \ln (x - 1) - \frac{x^{2}}{2} - x + C$

B. $x^{2} \ln (x - 1) - \frac{x^{2}}{2} - x + C$

C. $(x^{2} + 1) \ln (x - 1) - \frac{x^{2}}{2} - x + C$

D. $(x^{2} - 1) \ln (x - 1) - \frac{x^{2}}{2} + x + C$

Xem đáp án

Chọn A

Đặt $\{\begin{cases} u = \ln (x - 1) \\ d v = 2 x d x \end{cases} \Rightarrow \{\begin{cases} d u = \frac{1}{x - 1} d x \\ v = x^{2} - 1 \end{cases}$

Câu 8:

Tính $\int e^{\cos^{2} x} \sin 2 x d x$ bằng:

A. $e^{\sin x} + x + C$

B. $- e^{\cos^{2} x} + C$

C. $e^{- 2 \sin x} + C$

D. $- e^{\sin 2 x} + C$

Xem đáp án

Chọn B.

Câu 9:

Tính $\int e^{\sin^{2} x} \sin 2 x d x$ bằng:

A. $e^{\sin^{2} x} + C$

B. $e^{\sin 2 x} + C$

C. $e^{\cos^{2} x} + C$

D. $e^{2 \sin x} + C$

Xem đáp án

Chọn A.

Câu 10:

Biết hàm số $F (x) = - x \sqrt{1 - 2 x} + 2017$ là một nguyên hàm của hàm số $f (x) = \frac{a x + b}{\sqrt{1 - 2 x}}$ . Khi đó tổng của a và b là

A. 3.

B. 2.

C. 0.

D. 1.

Xem đáp án

Chọn B.

Ta có $F' (x) = (- x \sqrt{1 - 2 x} + 2017)' = \frac{3 x - 1}{\sqrt{1 - 2 x}}$

Nên a = 3; b = -1

=> a + b = 3 + (-1) = 2

Câu 11:

Tìm nguyên hàm của hàm số $f (x) = \frac{x^{3} - 2 x}{\sqrt{x^{2} + 1}}$

A. $F (x) = \frac{1}{3} (x^{2} - 8) \sqrt{x^{2} + 1} + C$

B. $F (x) = \frac{1}{3} x^{2} \sqrt{1 + x^{2}} + 8 \sqrt{1 + x^{2}} + C$

C. $F (x) = \frac{1}{3} (8 - x^{2}) \sqrt{x^{2} + 1} + C$

D. $F (x) = \frac{2}{3} (x^{2} - 8) \sqrt{1 + x^{2}} + C$

Xem đáp án

Câu 12:

Tìm nguyên hàm của hàm số: $I = \int \frac{d x}{{(x^{2} - 1)}^{2}}$

A. $\frac{1}{4} [\frac{- 1}{x - 1} - \ln |\frac{x + 1}{x - 1}| - \frac{1}{x + 1}] + C$

B. $\frac{1}{4} [\frac{1}{x - 1} + \ln |\frac{x + 1}{x - 1} - \frac{1}{x + 1}|] + C$

C. $\frac{1}{4} [\frac{- 1}{x - 1} + \ln |\frac{x + 1}{x - 1}| - \frac{1}{x + 1}] + C$

D. $\frac{1}{4} [\frac{- 1}{x - 1} + \ln |\frac{x + 1}{x - 1} - \frac{1}{x + 1}|] + C$

Xem đáp án

Chọn C.

Ta có:

Câu 13:

Tìm nguyên hàm của hàm số: $J = \int \frac{x^{3} + 2 x + 1}{x^{2} + 2 x + 1} d x$

A. $\frac{x^{2}}{2} + 12 x + 5 \ln |x + 1| + \frac{2}{x + 1} + C$

B. $\frac{x^{2}}{2} - 2 x + 5 \ln |x + 1| - \frac{2}{x + 1} + C$

C. $\frac{x^{2}}{2} - 2 x - 5 \ln |x + 1| + \frac{2}{x + 1} + C$

D. $\frac{x^{2}}{2} - 2 x + 5 \ln |x + 1| + \frac{2}{x + 1} + C$

Xem đáp án

Chọn D.

Ta có:

Câu 14:

Tính nguyên hàm của hàm số sau: $K = \int \frac{2 x^{2} + 1}{{(x + 1)}^{5}} d x$

A. $\frac{- 1}{{(x + 1)}^{2}} + \frac{4}{{(x + 1)}^{3}} - \frac{1}{x + 1} + C$

B. $\frac{- 1}{{(x + 1)}^{2}} + \frac{4}{3 {(x + 1)}^{3}} - \frac{1}{4 {(x + 1)}^{4}} + C$

C. $\frac{1}{{(x + 1)}^{2}} + \frac{4}{3 {(x + 1)}^{3}} + \frac{1}{4 {(x + 1)}^{4}} + C$

D. $\frac{- 1}{{(x + 1)}^{2}} + \frac{4}{3 {(x + 1)}^{3}} - \frac{1}{{(x + 1)}^{4}} + C$

Xem đáp án

Chọn B.

Ta phân tích $2 x^{2} + 1 = 2 {(x + 1)}^{2} - 4 (x + 1) + 3$

Suy ra:

Câu 15:

Tính $F (x) = \int \frac{\sin 2 x}{\sqrt{4 \sin^{2} x + 2 \cos^{2} x + 3}} d x$ . Hãy chọn đáp án đúng.

A. $F (x) = \sqrt{6 - \cos 2 x} + C$

B. $F (x) = \sqrt{6 - \sin 2 x} + C$

C. $F (x) = \sqrt{6 + \cos 2 x} + C$

D. $F (x) = - \sqrt{6 - \sin 2 x} + C$

Xem đáp án

Chọn A.

Câu 16:

Biết hàm số $F (x) = (m x + n) \sqrt{2 x - 1}$ là một nguyên hàm của hàm số $f (x) = \frac{1 - x}{\sqrt{2 x - 1}}$ . Khi đó tích của m và n là

A. 2

B. -2

C. $- \frac{2}{3}$

D. $- \frac{2}{9}$

Xem đáp án

Chọn D.

Cách 1: Tính $\int \frac{1 - x}{\sqrt{2 x - 1}} d x = (\frac{- 1}{3} x + \frac{2}{3}) \sqrt{2 x - 1} + C$

Suy ra: m= $\frac{- 1}{3}$ ; n= $\frac{2}{3}$ $\Rightarrow m . n = - \frac{2}{9}$

Cách 2: Tính

Câu 17:

Biết hàm số F(x) là một nguyên hàm của hàm số $f (x) = \frac{\ln x}{x \sqrt{\ln^{2} x + 3}}$ có đồ thị đi qua điểm (e; 2016) . Khi đó hàm số F(1) là

A. $\sqrt{3} + 2014$

B. $\sqrt{3} + 2016$

C. $2 \sqrt{3} + 2014$

D. $2 \sqrt{3} + 2016$

Xem đáp án

Chọn A.

Đặt $t = \sqrt{\ln^{2} x + 3}$ và tính được $F (x) = \sqrt{\ln^{2} x + 3} + C$

$F (e) = 2016 \Rightarrow C = 2014 \Rightarrow F (x) = \sqrt{\ln^{2} x + 3} + 2014 \Rightarrow F (1) = \sqrt{3} + 2014$

Câu 18:

Một nguyên hàm F(x) của hàm số $f (x) = \ln (x + \sqrt{x^{2} + 1})$ thỏa mãn F(0) = 1. Chọn kết quả đúng

A. $F (x) = x \ln (x + \sqrt{x^{2} + 1}) - \sqrt{x^{2} + 1} + 2$

B. $F (x) = x \ln (x + \sqrt{x^{2} + 1}) - \sqrt{x^{2} + 1} - 2$

C. $F (x) = x \ln (x + \sqrt{x^{2} + 1}) - \sqrt{x^{2} + 1} + 1$

D. $F (x) = x \ln (x + \sqrt{x^{2} + 1}) - \sqrt{x^{2} + 1}$

Xem đáp án

Chọn A.

Đặt $u = \ln (x + \sqrt{x^{2} + 1}), d v = d x$ ta được

F(x)= $x \ln (x + \sqrt{x^{2} + 1}) - \sqrt{x^{2} + 1} + C$

Vì F(0) = 1 nên C = 2

Vậy

Câu 19:

Một nguyên hàm F(x) của hàm số $f (x) = \frac{x}{\cos^{2} x}$ thỏa mãn $F (π) = 2017$ . Khi đó F(x) là hàm số nào dưới đây?

A. F(x) = xtanx + ln|cosx| + 2017.

B. F(x) = xtanx – ln|cosx| + 2018.

C. F(x) = xtanx + ln|cosx| + 2016.

D. F(x) = xtanx – ln|cosx| + 2017.

Xem đáp án

Câu 20:

Tính $F (x) = \int \frac{1 + x \sin x}{\cos^{2} x} d x$ . Chọn kết quả đúng

A. $F (x) = \tan x + \frac{x}{\cos x} + \frac{1}{2} |\frac{\sin x - 1}{\sin x + 1}| + C$

B. $F (x) = \tan x - \frac{x}{\cos x} + \frac{1}{2} |\frac{\sin x - 1}{\sin x + 1}| + C$

C. $F (x) = \tan x + \frac{x}{\cos x} - \frac{1}{2} |\frac{\sin x - 1}{\sin x + 1}| + C$

D. $F (x) = \tan x - \frac{x}{\cos x} - \frac{1}{2} |\frac{\sin x - 1}{\sin x + 1}| + C$

Xem đáp án

Câu 21:

Một nguyên hàm F(x) của hàm số $f (x) = \sin x + \frac{1}{\cos^{2} x}$ thỏa mãn điều kiện $F (\frac{π}{4}) = \frac{\sqrt{2}}{2}$ là

A. $F (x) = - \cos x + \tan x + 1 - \sqrt{2}$

B. $F (x) = \cos x + \tan x + \sqrt{2} - 1$

C. $F (x) = - \cos x + \tan x + \sqrt{2} - 1$

D. $F (x) = - \cos x + \tan x$

Xem đáp án

Chọn C.

Ta có

Vậy

Câu 22:

Một nguyên hàm F(x) của hàm số $f (x) = 2 \sin 5 x + \sqrt{x} + \frac{3}{5}$ thỏa mãn đồ thị của hai hàm số F(x) và f(x) cắt nhau tại một điểm nằm trên trục tung là:

A. $- \frac{2}{5} \cos 5 x + \frac{2}{3} x \sqrt{x} + \frac{3}{5} x + 1$

B. $\frac{2}{5} \cos 5 x + \frac{2}{3} x \sqrt{x} + \frac{3}{5} x + 1$

C. $10 \cos 5 x + \frac{1}{2 \sqrt{x}} + \frac{3}{5} x + 1$

D. $- \frac{2}{5} \cos 5 x + \frac{2}{3} x \sqrt{x} + \frac{3}{5} x$

Xem đáp án

Chọn A.

Ta có F(x)= $- \frac{2}{5} \cos 5 x + \frac{2}{3} x \sqrt{x} + \frac{3}{5} x + C$

và F(0) = f(0) ⇔ C = 1

Vậy F(x)= $- \frac{2}{5} \cos 5 x + \frac{2}{3} x \sqrt{x} + \frac{3}{5} x + 1$

Câu 23:

Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính $I = \int_{- 1}^{2} [f (x) + 2 x] d x$ biết F(-1) = 1, F(2) = 4.

A. I = 6.

B. I = 10.

C. I = 3.

D. I = 9.

Xem đáp án

Chọn A

Ta có

Câu 24:

Cho $\int_{1}^{3} f (x) d x = - 5, \int_{1}^{3} [f (x) - 2 g (x)] d x = 9 .$ Tính $I = \int_{1}^{3} g (x) d x$

A. I = 14.

B. I = -14.

C. I = 7.

D. I = -7.

Xem đáp án

Chọn D

Câu 25:

Cho hàm số f(x) liên tục trên đoạn [0; 10] thỏa mãn $\int_{0}^{10} f (x) d x = 7, \int_{2}^{6} f (x) d x = 3$ . Tính $P = \int_{0}^{2} f (x) d x + \int_{6}^{10} f (x) d x$ .