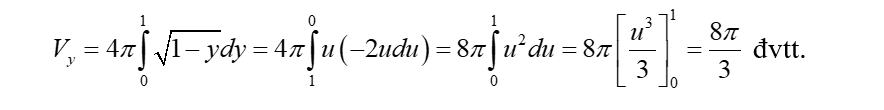150 câu trắc nghiệm Nguyên hàm - Tích phân nâng cao-P5 (có đáp án)
-
1611 lượt thi
-
30 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = , biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục Ox tại điểm có hoành độ x ( ) là một hình chữ nhật có độ dài hai cạnh là x và
 Xem đáp án
Xem đáp án
Chọn C.
Ta có diện tích thiết diện của vật thể cắt bởi mặt phẳng (P) là:
S(x) = x nên thể tích cần tính là:
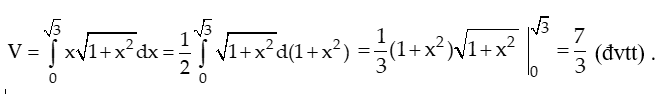
Câu 2:
Cho parabol (P): y= . Gọi (d) là tiếp tuyến với (P) qua O có hệ số góc k > 0. Xác định m để thể tích vật thể được sinh ra khi hình phẳng giới hạn bởi (P), (d) và trục Oy quay quanh trục Oy bằng 6.
 Xem đáp án
Xem đáp án
Chọn C.
Tiếp tuyến (d) qua O có dạng y = kx, k > 0. (d) tiếp xúc với (P) tại điểm có hoành độ
khi hệ có nghiệm tức là phương trình có nghiệm
suy ra k =
Phương trình (d): y = 2
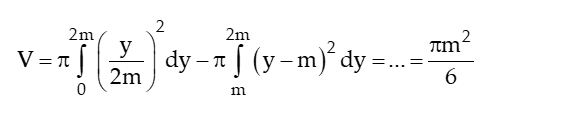
Mà V = 6 suy ra m = 6 mà m0 suy ra m = 6
Vậy m = 6 thỏa mãn bài toán.
Câu 3:
Diện tích hình phẳng giới hạn bởi các đường thẳng y = 1, y = x và đồ thị hàm số trong miền là phân số tối giản . Khi đó b - a bằng
 Xem đáp án
Xem đáp án
Chọn D
Ta có
Vậy a = 5; b = 6 bà b - a = 1
Câu 4:
Diện tích hình phẳng giới hạn bởi các đường thẳng và y = là (với là phân số tối giản) . Khi đó a + 2b bằng
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
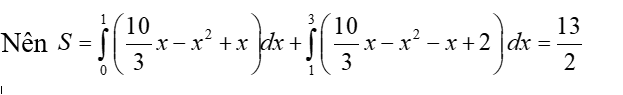
Suy ra a=13 ; b=2 và a+2b=17.
Câu 5:
Cho hàm số f(x) liên tục trên R và f(2) = 16, . Tính I =
 Xem đáp án
Xem đáp án
Chọn D.
Đặt t = 2x => dt = 2dx, Đổi cận x = 0 <=> t = 0, x = 1 <=> t = 2
I =
Đặt
I =
Câu 6:
Cho hàm số f(x) liên tục trên R và các tích phân = 4 và , tính tích phân I =
 Xem đáp án
Xem đáp án
Chọn A.
Đặt t = tan x => dt = (1+ x) dx =>
Đổi cận x = 0 => t = 0 và x =
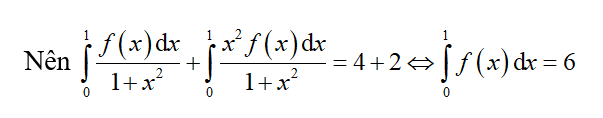
Câu 7:
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = xsin2x, y = 2x,
 Xem đáp án
Xem đáp án
Chọn C.
Phương trình hoành độ giao điểm: x sin 2x = 2x x (sin2x-2) = 0 x = 0 hoặc sin2x = 2 (VN)
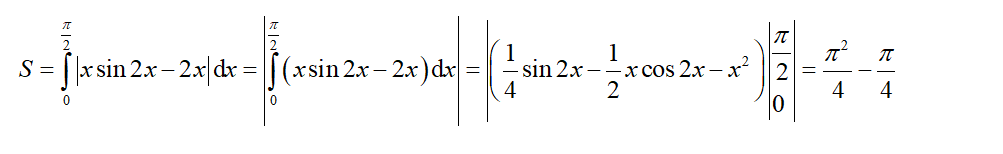
Câu 8:
Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ thị và y =
 Xem đáp án
Xem đáp án
Chọn A
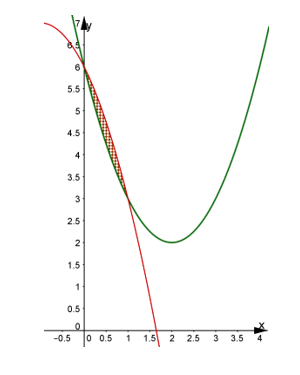
Xét phương trình hoành độ giao điểm: x = 0 hoặc x =1
Thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ thị y = là
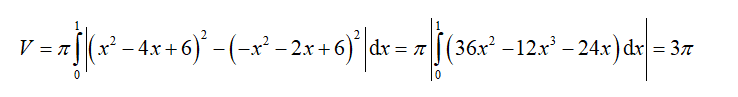
Câu 9:
Biết là ( a,b ). Tính P = a + b.
 Xem đáp án
Xem đáp án
Chọn C.
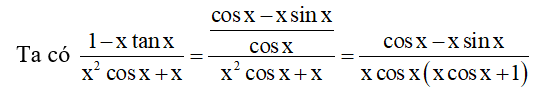
Đặt t = xcosx => dt = (cosx – x sinx)dx
Do đó P = a + b = 3 + 1 = 4.
Câu 10:
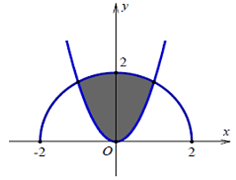
Cho (H) là hình phẳng giới hạn bởi parabol y = và nửa đường tròn có phương trình y = với (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
 Xem đáp án
Xem đáp án
Chọn D.
Hoành độ giao điểm của (P) và ( C) là nghiệm của <=> x = 1 hoặc x = -1
Khi đó, diện tích cần tính là H = 2. () =
Câu 11:
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [1; 4], f(1) = 12 và .Giá trị của f(4) bằng
 Xem đáp án
Xem đáp án
Chọn A.
Ta có
Câu 13:
Một đám vi khuẩn tại ngày thứ x có số lượng là N(x). Biết rằng N'(x) = và lúc đầu số lượng vi khuẩn là 5000 con. Vậy ngày thứ 12 số lượng vi khuẩn (sau khi làm tròn) là bao nhiêu con?
 Xem đáp án
Xem đáp án
Chọn A.
Ta có
=> N(12) = 2000 ln13+ 5000
Câu 16:
Xét hàm số f(x) liên tục trên đoạn [0; 1] và thỏa mãn 2f(x) + 3f(1-x) = .Tính I =
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
Câu 17:
Cho hàm số y = f(x) có với mọi . Hỏi khẳng định nào dưới đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Chọn A.
Đầu tiên ta phải nhận dạng được f(5) - f(2) =
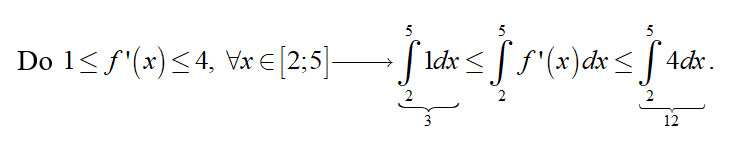
Vậy
Câu 18:
Cho m thỏa mãn . Nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Chọn A.
và = 12
Suy ra: m2 – 6m + 21 = 12 m2 – 6m + 9 = 0 m = 3
Khi đó:
Câu 19:
Tính tích phân được kết quả I = aln3 + bln5 với a, b là các số hữu tỉ. Giá trị của a2 + ab + 3b2 là
 Xem đáp án
Xem đáp án
Chọn D.
Đặt Đổi cận
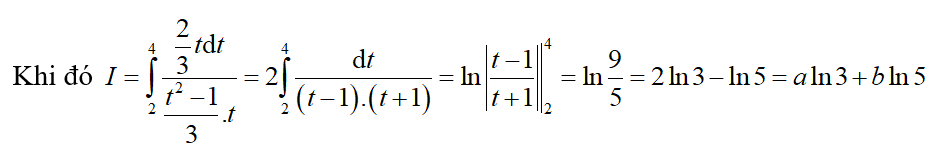
Suy ra a = 2; b = -1 ⇒ a2 + ab + 3b2 = 5.
Câu 20:
Cho . Tính
 Xem đáp án
Xem đáp án
Chọn A.
Cách 1: Đặt t = ⇒ 2t = x ⇔ dx = 2dt
Khi đó
Cách 2: Chọn f(x) = -3 thỏa mãn
Suy ra
Câu 21:
Cho hàm số f(x) thỏa mãn và 2f(1) – f(0) = 2. Tính I =
 Xem đáp án
Xem đáp án
Chọn D.
Đặt
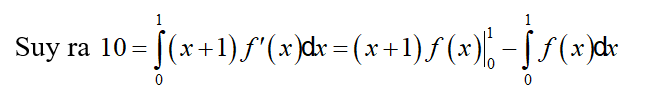
⇔ 10 = 2f(1) – f(0) – I ⇔ 10 = 2 – I ⇔ I = -8.
Câu 22:
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và = 3 . Tính tích phân hàm:
 Xem đáp án
Xem đáp án
Chọn C.
Đặt
Suy ra:
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.
Câu 23:
Tính S hình phẳng được giới hạn bởi các đường ; y = 0; x=1
 Xem đáp án
Xem đáp án
Chọn A.
Ta có: . Rõ ràng với mọi x ∈ [0; 1]
Do đó diện tích của hình phẳng là S = =
Đặt t = , ta có khi x = 0 thì t = , khi x = 1 thì t = 2 và 3x = t2 - 1
Suy ra 3x ln3dx = 2tdt, hay . Khi đó ta có
Câu 24:
Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x2 , y = 4x - 4 và y = -4x - 4
 Xem đáp án
Xem đáp án
Chọn B.
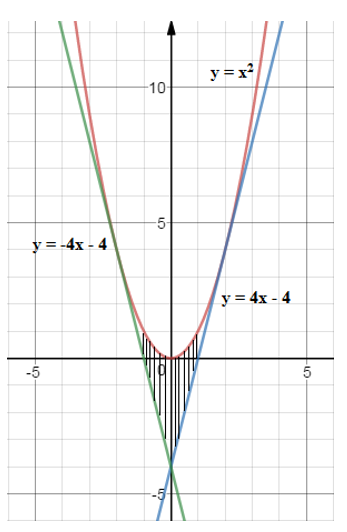
Ta thấy đường thẳng y = -4x - 4 và đường thẳng y = 4x - 4 lần lượt là hai tiếp tuyến của đồ thị hàm số y = x2 tại các tiếp điểm có hoành độ x = -2 và x = 2.
Do tính đối xứng qua Oy của parabol y = x2 nên diện tích hình phẳng cần tìm bằng:
S =
Câu 25:
Tính diện tích giới hạn bởi các đường cong y = (x - 1)lnx và y = x - 1.
 Xem đáp án
Xem đáp án
Chọn A.
+) Xét phương trình: (x - 1)lnx = x - 1 ⇔ x = 1 hoặc x = e.
+ ) Diện tích cần tìm là:
Câu 26:
Tính diện tích giới hạn bởi các đường cong y=(e+1)x; y = (ex + 1)x
 Xem đáp án
Xem đáp án
Chọn D.
Hoành độ giao điểm của hai đường là nghiệm của phương trình (e+1)x = <=> x = 0 hoặc x =1
Diện tích cần tính là S =
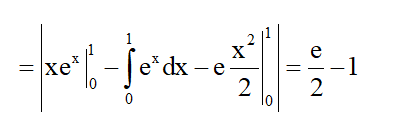
Câu 27:
Tính diện tích giới hạn bởi các đường cong y = (x - 1)ln(x + 1) và trục hoành
 Xem đáp án
Xem đáp án
Chọn C.
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
(x – 1) ln(x + 1) = 0 <=> x = 1 hoặc x = 0
→ Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = (x – 1) ln(x = 1) và trục hoành là
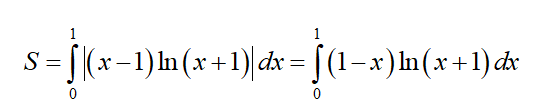
Đặt
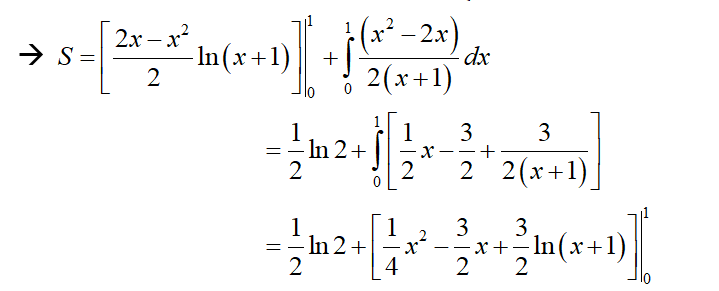
= =
Câu 28:
Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi y =
Và y = 0; x = 0; x = 1 xung quanh Ox
 Xem đáp án
Xem đáp án
Chọn C
Thể tích khối tròn xoay là V =
Đặt t = , ta có khi x = 0 thì t = 2, khi x = 1 thì t = 1 và x = nên dx = -
Khi đó ta có:
Câu 29:
Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi y = trục hoành và x = 1 xung quanh trục hoành.
 Xem đáp án
Xem đáp án
Chọn A.
Ta có và Do đó thể tích khối tròn xoay cần tính là:
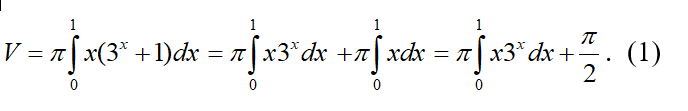
Tính . Đặt u = x , dv =
Theo công thức tích phân từng phần ta có:
Thay vào (1) ta được : V =
Câu 30:
Gọi D là miền giới hạn bởi (P): y = 2x - x2 và trục hoành. Tính thể tích vật thể V do ta quay (D) xung quanh trục Oy.
 Xem đáp án
Xem đáp án
Chọn B.
0 ≤ x ≤ 2 thì y = 2x – ⇔ – 2x + y = 0
Phương trình bậc hai theo y. Ta có
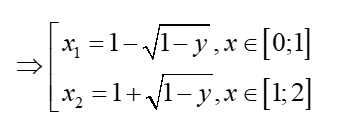
Đặt u =
Đổi cận : khi y = 1 => u = 0; khi y = 0 => u = 1