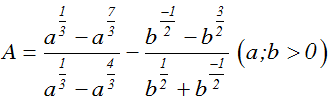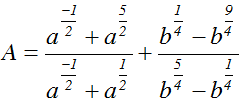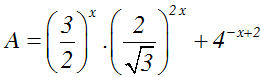200 câu trắc nghiệm Hàm số mũ và Logarit cơ bản (P1)
-
2132 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tìm tập xác định D của hàm số y = ( x2 - 3x + 2) 100
 Xem đáp án
Xem đáp án
Chọn C.
Hàm số y = xα với α nguyên dương, xác định với mọi x.
Do đó hàm số y = ( x2 - 3x + 2) 100 xác định với mọi x.
Câu 2:
Tìm tập xác định D của hàm số y = ( x3 - 8) -100
 Xem đáp án
Xem đáp án
Chọn B.
Hàm số y = xα với α nguyên âm, xác định với ∀ x ≠ 0.
Hàm số y = ( x3 - 8)-100 xác định x3 – 8 ≠ 0 hay x ≠ 2.
Câu 3:
Tìm tập xác định D của hàm số y = ( x3 - 8)0
 Xem đáp án
Xem đáp án
Chọn B.
Hàm số y = xα với α= 0 xác định với x ≠ 0.
Hàm số đã cho xác định khi và chỉ khi x3 – 8 ≠ 0 hay x ≠ 2.
Câu 4:
Tìm x để biểu thức (2x - 1)– 2 có nghĩa:
 Xem đáp án
Xem đáp án
Chọn A.
Biểu thức ( 2x - 1)– 2 có nghĩa khi 2x – 1 ≠ 0 hay x ≠
Câu 5:
Tìm tập xác định D của hàm số
 Xem đáp án
Xem đáp án
Chọn C.
Hàm số y = xα với α không nguyên thì cơ số phải dương.
Do đó hàm số đã cho xác định khi x2 - 6x + 8 > 0
Suy ra x > 4 hoặc x < 2.
Câu 6:
Tìm x để biểu thức có nghĩa:
 Xem đáp án
Xem đáp án
Chọn A.
Biểu thức có nghĩa khi và chỉ khi x2 + x + 1 > 0 ( luôn đúng với mọi x).
Câu 11:
Tìm biểu thức không có nghĩa trong các biểu thức sau:
 Xem đáp án
Xem đáp án
Chọn B.
Vì nên (-3) -1/3 không có nghĩa.
Câu 14:
Cho , khi đó f( 1,3) bằng:
 Xem đáp án
Xem đáp án
Chọn B.
Vì x = 1,3 > 0 nên ta có:
Do đó f(1,3) = 1,3.
Câu 15:
Cho . Khi đó f( 2,7) bằng
 Xem đáp án
Xem đáp án
Chọn C.
Vì x = 2,7 > 0 nên ta có:
do đó: f( 2,7) = 2,7.
Câu 21:
Trong các biểu thức sau biểu thức nào không có nghĩa
 Xem đáp án
Xem đáp án
Chọn C.
Ta có:
xa với a là số 0 hoặc số nguyên âm xác định với a ≠ 0;
xa ( với a không là số nguyên ) xác định với a > 0
Vì vậy 0 -2016 không có nghĩa.
Câu 27:
Cho 2x = 3.Tính giá trị biểu thức A = 4x + 3.2-x - 1
 Xem đáp án
Xem đáp án
Chọn B.
Ta có A = 4x + 3.2-x - 1
Câu 30:
Cho 2x = a; 3x = b. Hãy biểu diễn A = 24x + 6x + 9x theo a và b.
 Xem đáp án
Xem đáp án
Chọn A.
Ta có: A = ( 23.3) x + ( 2.3) x + ( 32)x
= 23x.3x + 2x.3x + 32x =


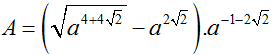 ta được:
ta được: