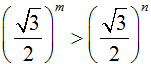30 câu hỏi trắc nghiệm thuộc 200 câu trắc nghiệm Hàm số mũ và Logarit cơ bản (P2)

Câu 1:

Cho ${(\sqrt{2} + 1)}^{x} = 3$ . hãy tính giá trị của biểu thức

A. A = 18

B. A = 0

C. A = 82/9

D. A = 28/9

Xem đáp án

Chọn C.

Ta có:

Do đó

Câu 2:

Cho 5^x= 4 hãy tính giá trị của biểu thức $T = 25^{x} - 5^{2 - x} + 5^{\frac{x}{2}}$

A. T = 14

B. T = 47/4

C. T = 118

D. T = 6

Xem đáp án

Chọn B.

Ta có:

Câu 3:

Cho a = 2^x; b = 5^x. Hãy biểu diễn T = 20^x+ 50^xtheo a và b.

A. T = ab(a + b)

B. $T = \frac{a b}{a + b}$

C. T = a²+ ab²

D. T = ab + a²b

Xem đáp án

Chọn A.

Ta có: T = ( 2².5) ^x+ ( 5².2) ^x= 2^2x.5^x+ 5^2x.2^x= a²b +ab²= ab(a + b)

Câu 4:

Cho $a^{- \sqrt{3}} > a^{- \sqrt{2}}$ và a^x> b^x. Khẳng định nào sau đây là đúng

A. 1 > a > b > 0

B. 1 > b > a > 0

C. a > b > 1

D. b > a > 1

Xem đáp án

Chọn A.

Ta có: nên

Mặt khác a^x> b^x nên a > b do vậy 1 > a > b > 0

Câu 5:

So sánh hai số m và n nếu ${(\sqrt{2})}^{m} < {(\sqrt{2})}^{n}$

A. m > n.

B. m = n

C. m < n

D. Không so sánh được

Xem đáp án

Chọn C.

Do nên

Câu 6:

So sánh hai số m và n nếu

A. Không so sánh được.

B. m = n.

C. m > n.

D. m < n.

Xem đáp án

Chọn D.

Do nên

Câu 7:

So sánh hai số m và n nếu

A. m < n

B. m = n

C. m > n

D. Không so sánh được

Xem đáp án

Chọn A.

Do nên

Câu 8:

Cho ${(a - 1)}^{\frac{- 3}{4}} > {(a - 1)}^{\frac{- 4}{5}}$ và $\sqrt{b^{3}} > \sqrt[3]{b^{2}}$ . Khẳng định nào sau đây là đúng

A. a, b >1

B. 0 < a < 2; b > 1

C. 0 < a < 2; b < 1

D. a > 2; b > 1

Xem đáp án

Chọn D.

Ta có: nên

Mặt khác

Do đó a > 2; b > 1

Câu 9:

Khẳng định nào dưới đây là đúng

A. ( x²+ 1) ²⁰¹⁷ > ( x²+ 1) ²⁰¹⁷

B.

C. ${(\sqrt{2} + 1)}^{x^{2} + 1} > {(\sqrt{2} - 1)}^{1 - x^{2}} (\forall x \in R)$

D. Cả A và C đều đúng

Xem đáp án

Chọn C.

- A sai vì khi x = 0 không thỏa mãn

- C đúng vì

nên

Câu 10:

Kết luận nào đúng về số thực a nếu ( 2a + 1) ^-3> ( 2a + 1)^-1

A. $[\begin{matrix} - \frac{1}{2} < a < 0 \\ a < - 1 \end{matrix}$

B. -1/2 < a < 0.

C. $[\begin{matrix} o < a < 1 \\ a < - 1 \end{matrix}$

D. a < -1.

Xem đáp án

Chọn A.

Do -3 < -1 và số mũ nguyên âm nên ( 2a+ 1) ^-3> ( 2a+ 1) ^-1 khi

Câu 11:

Kết luận nào đúng về số thực a nếu

A. 0 < a < 1

B. a > 0

C. a > 1

D. a < 0

Xem đáp án

Chọn C.

Ta có

Do và có số mũ không nguyên nên a^0,2 < a² khi a > 1.

Câu 12:

Kết luận nào đúng về số thực a nếu

A. a < 1

B. a > 0

C. 0 < a < 1

D. a <0

Xem đáp án

Chọn D.

Do $- \frac{1}{3} > - \frac{1}{2}$ và số mũ không nguyên . Khi và chỉ khi $\{\begin{cases} 1 - a > 0 \\ 1 - a > 1 \end{cases} \Leftrightarrow 1 - a > 1 \Leftrightarrow a < 0$

Câu 13:

Kết luận nào đúng về số thực a nếu

A. a > 1

B.0 < a < 1

C. 1 < a < 2

D. a < 1

Xem đáp án

Chọn C.

Do ¾ < 2 và có số mũ không nguyên ⇒

Khi và chỉ khi 0 < 2 - a, 1 hay 2 > a > 1

Câu 14:

Cho ${(a - 2)}^{- \sqrt{2}} > \sqrt{{(a - 2)}^{3}}$ và ${(a - 1)}^{- \sqrt{2}} > {(b - 1)}^{- \sqrt{2}}$ . Khẳng định nào dưới đây là đúng?

A. 2 < a < b < 3

B. 2 < b < a < 3

C. b > a > 3

D. a > b > 3

Xem đáp án

Chọn A.

Ta có:

Suy ra 2 < a < 3.

Mặt khác

⇔ a – 1 < b – 1 ⇔ a < b

Do đó 2 < a < b < 3.

Câu 15:

Đơn giản biểu thức ta được:

A.

B.

C.

D. a – b

Xem đáp án

Chọn B.

Ta có:

Câu 16:

Trong các số a thoã mãn điều kiện dưới đây. Số nào lớn hơn 1.

A. log₂a = -2

B. log₃a = π

C. log₄a²= -1

D. log₃a = - 0, 4

Xem đáp án

Chọn B.

Ta có

Câu 17:

Trong các số a thoả mãn điều kiện dưới đây. Số nào nhỏ hơn 1.

A.

B. log_a5 = 2

C. log₃5 = a

D.

Xem đáp án

Chọn D.

Ta có

Câu 18:

Giá trị của biểu thức là

A. a = 4/3

B. a = 3/4

C. a = 8/9

D. a = 9/8

Xem đáp án

Chọn D.

Ta có

Câu 19:

Giá trị của biểu thức là:

A. A = 1/4

B. A = 1/3

C. A = 1/2

D. A = 3/4

Xem đáp án

Chọn A.

Ta có:

$\log_{a} \frac{\sqrt{a^{3}}}{a \sqrt[4]{a}} = \log_{a} \frac{a^{\frac{3}{2}}}{a . a^{\frac{1}{4}}} = \log_{a} a^{\frac{3}{2} - (1 + \frac{1}{4})} = \log_{a} a^{\frac{1}{4}} = \frac{1}{4}$

Câu 20:

Giá trị của biểu thức là:

A. A = 17/5

B. A = 37/10

C. A = 21/5

D. A = 39/10

Xem đáp án

Chọn B.

Ta có:

Câu 21:

Cho và ( với x ; y > 0 và y ≠ 1). Tính A = a + b bằng

A. A = 9/4

B. A = 3/2

C. A = 15/8

D. A = 17/8

Xem đáp án

Chọn D.

Ta có:

Lại có:

Câu 22:

Cho và ( với x ; y > 0 ; y ≠ 1). Tính A = m + n

A. A = 23/12

B . A = 1

C. A = 3

D. A = 7/3

Xem đáp án

Chọn A.

Ta có:

Lại có

Do đó

Câu 23:

Thu gọn biểu thức ta được:

Xem đáp án

Đáp án D

Ta có: A ${(a^{3} \sqrt{a})}^{\log_{a} b} + {(\sqrt[3]{b^{2}})}^{\log_{b} a} = {(a^{\frac{7}{2}})}^{\log_{a} b} + {(b^{\frac{2}{3}})}^{\log_{b} a} = a^{\log_{a} b^{\frac{7}{2}}} + b^{\log_{b} a^{\frac{2}{3}}} = b^{\frac{7}{2}} + a^{\frac{2}{3}} = \sqrt{b^{7}} + \sqrt[3]{a^{2}}$