30 câu hỏi trắc nghiệm thuộc 200 câu trắc nghiệm Hàm số mũ và Logarit cơ bản (P3)

Câu 1:

Với giá trị nào của x thì biểu thức $A = \log_{\frac{1}{2}} \frac{x - 1}{3 + x}$ xác định?

A.-3≤ x≤ 1.

B.

C.

D. .-3< x < 1.

Xem đáp án

Biểu thức có nghĩa khi

Chọn B.

Câu 2:

Với giá trị nào của x thì biểu thức: f( x) = log₆( 2x- x²) xác định?

A.0<x< 2.

B. x> 2.

C.-1< x< 1.

D.x< 3.

Xem đáp án

Biểu thức có nghĩa khi 2x- x²> 0 hay 0< x< 2

Chọn A.

Câu 3:

Với giá trị nào của x thì biểu thức: f(x) = log₅( x³-x²-2x) xác định?

A. 0<x < 1.

B x> 1

C.

D.

Xem đáp án

Biểu thức có nghĩa khi: x³- x²-2x> 0 hay x( x²-x-2) > 0

Cách 1: Ta có bảng xét dấu sau:

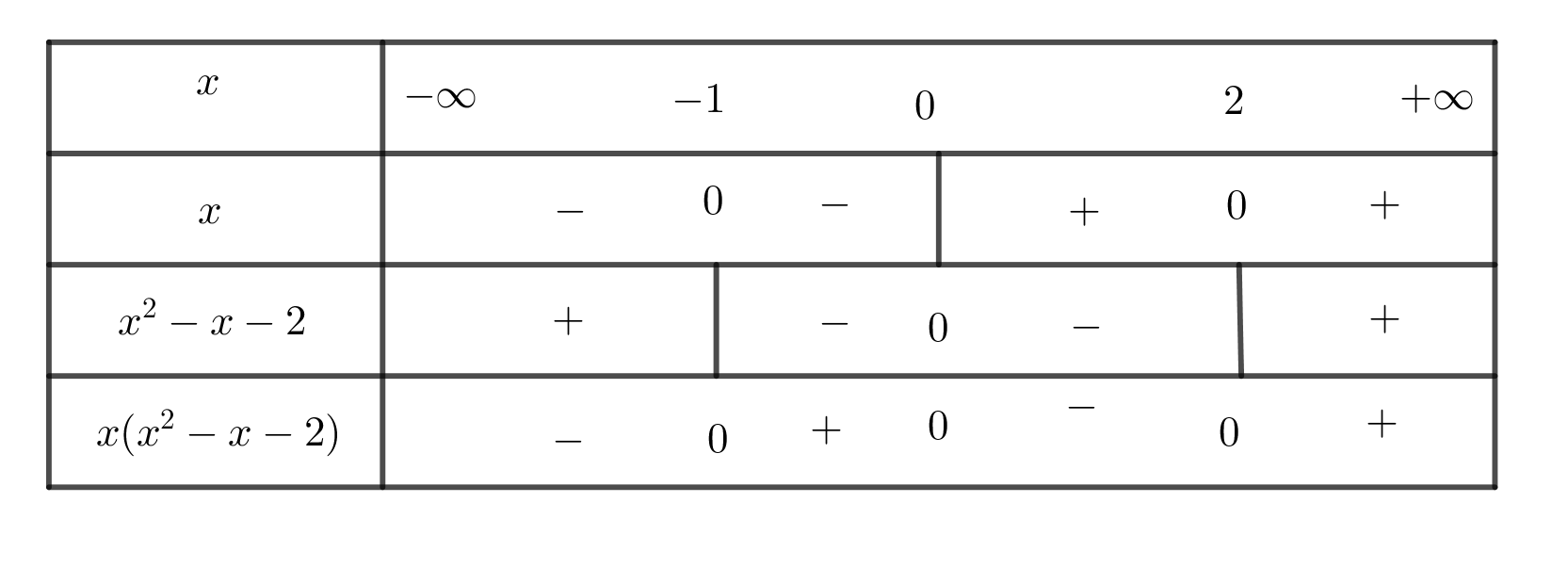
Suy ra: -1 < x < 0 hoặc x > 2

Vậy để biểu thức có nghĩa thì $x \in (- 1; 0) \cup (2; + \infty)$

Cách 2: sử dụng máy tính giải bất phương trình bậc 3.

Chọn C.

Câu 4:

Điều kiện xác định của biểu thức $T = l o g \sqrt{(x^{2} - 4) (x^{2} - 6 x + 9)}$ là

A.

B. x>3

C.

D.

Xem đáp án

+ Biểu thức có nghĩa khi ( x²- 4)( x²-6x+ 9) >0

Hay ( x²-4) ( x-3)²> 0

Ta có bảng xét dấu sau:

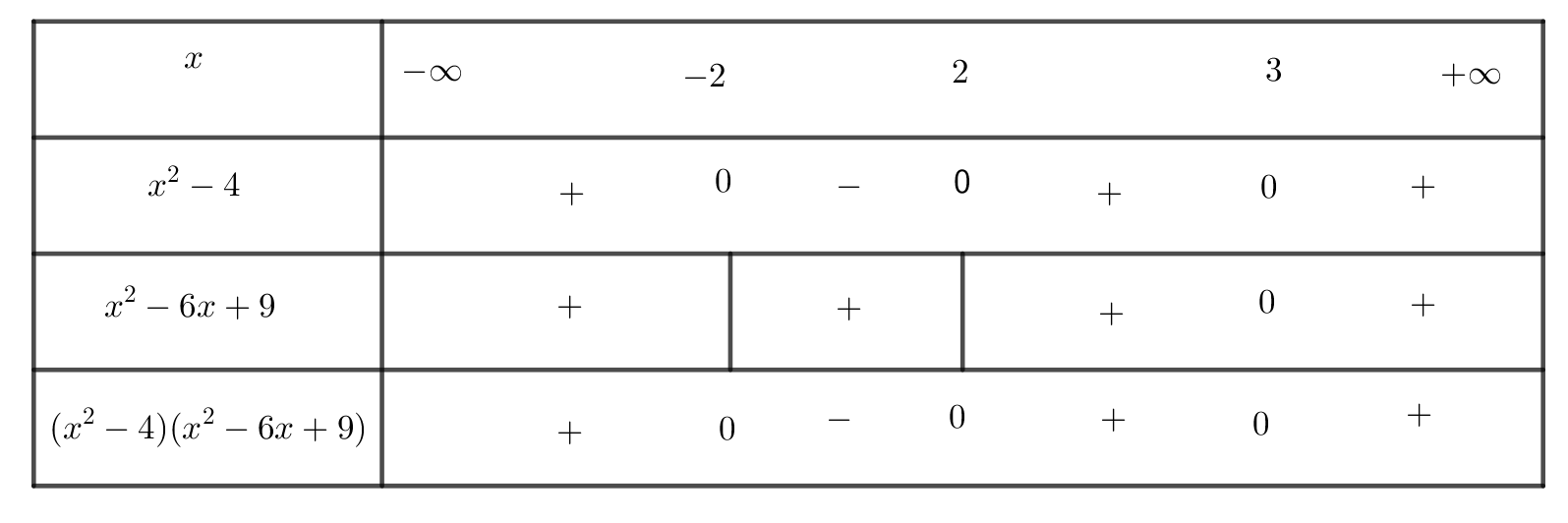
Suy ra biểu thức có nghĩa khi $x \in (- \infty; - 2) \cup (2; 3) \cup (3; + \infty)$

Chọn D.

Câu 5:

Cho $\log_{2} x = 2 \log_{2} \sqrt[3]{a^{2}} + 3 \log_{2} \frac{1}{b^{2} \sqrt{b}} (a; b > 0)$ Khi đó:

A.

B.

C.

D. x= ab

Xem đáp án

Ta có:

$\log_{2} x = 2 \log_{2} \sqrt[3]{a^{2}} + 3 \log_{2} \frac{1}{b^{2} \sqrt{b}} (a; b > 0), x > 0 \Leftrightarrow \log_{2} x = \log_{2} a^{\frac{4}{3}} + \log_{2} b^{- \frac{15}{2}} \Leftrightarrow \log_{2} x = \log_{2} a^{\frac{4}{3}} . b^{- \frac{15}{2}} \Leftrightarrow \log_{2} x = \log_{2} a^{\frac{4}{3}} . b^{- \frac{15}{2}} \Leftrightarrow x = a^{\frac{4}{3}} . b^{- \frac{15}{2}}$

Do đó $x = a^{\frac{4}{3}} . b^{\frac{- 15}{2}}$

Chọn B

Câu 6:

Cho log_ax= m và log_abx= n ( a; b> 0) . Khi đó log_bx bằng

A.

B.

C.

D.

Xem đáp án

Ta có: log_ax= m và log_abx= n nên log_xa = $\frac{1}{m}$ và log_x(ab)= . $\frac{1}{n}$

Đáp án B

Câu 7:

Cho x= 2000! . Giá trị của biểu thức $A = \frac{1}{\log_{2} x} + \frac{1}{\log_{3} x} + . . . + \frac{1}{\log_{2000} x}$ là:

A. 1

B. -1

C.1000

D.2000

Xem đáp án

Do: log_ab.log_ba = 1 nên từ giải thiết ta suy ra;

A= log_x2+ log_x3+.....+ log_x2000= log_x(1.2.3...2000) = log_xx=1

Chọn A

Câu 8:

Rút gọn biểu thức $A = \log_{2} \sqrt{a} + \log_{4} \frac{1}{a^{2}} - \log_{\sqrt{2}} a^{8} (a > 0)$ ta được:

A.

B

C.

D.

Xem đáp án

Chọn B

Câu 9:

Rút gọn biểu thức A= log₄a- log₈a+ log₁₆a² ( a> 0) ta được:

A. A= log₂x

B.

C.

D.

Xem đáp án

Ta có:

A= log₄a- log₈a+ log₁₆a² =

Chọn D.

Câu 10:

Cho $\log_{2} x = \sqrt{2}$ . Tính giá trị của biểu thức $A = \log_{2} x^{2} + \log_{\frac{1}{2}} x^{3} + \log_{4} x$

A. A = $- \sqrt{2}$

B. A = -2 $\sqrt{2}$

C. $A = \frac{- \sqrt{2}}{2}$

D. A = $\frac{- \sqrt{2}}{4}$

Xem đáp án

Chọn C

Câu 11:

Rút gọn biểu thức $A = \log_{8} x \sqrt{x} - \log_{\frac{1}{4}} x^{2} (x > 0)$ Ta được:

A. $A = \frac{3}{2} \log_{2} x$

B. $A = - \frac{1}{2} \log_{2} x$

C. $A = \log_{2} x$

D. $A = \frac{2}{3} \log_{2} x$

Xem đáp án

Chọn A

Câu 12:

Rút gọn biểu thức A= log₃x.log₂3+ log₅x.log₄5 ( x> 0) ta được:

A.

B.

C.A= 2log₂x

D.

Xem đáp án

Áp dụng công thức : log_ab. log_bc= log_ac, ta có:

A= log₃x.log₂3+ log₅x.log₄5= log₂x+ log₄x

Chọn A.

Câu 13:

Cho $\log_{3} x = 1 + \sqrt{2}$ . Tính giá trị biểu thức: $A = \log_{3} x^{3} + \log_{\frac{1}{3}} x + \log_{9} x^{2}$

A. $A = 2 (1 + \sqrt{2})$

B. $A = 1 + \sqrt{2}$

C. A = -2(1+ $\sqrt{2}$ )

D. A = 3(1 + $\sqrt{2}$ )

Xem đáp án

Đáp án D

Ta có:

Câu 14:

Tính giá trị của biểu thức $P = \log_{a} \frac{1}{b^{3}} \log_{\sqrt{b}} a^{3} (1 ≢ a; b > 0)$

A. -18

B. $\frac{- 1}{2}$

C. 18

D. $\frac{1}{2}$

Xem đáp án

Đáp án A

Ta có:

$P = \log_{a} \frac{1}{b^{3}} \log_{\sqrt{b}} a^{3} (1 ≢ a; b > 0) = \log_{a} b^{- 3} \log_{b^{\frac{1}{2}}} a^{3} = (- 3) \log_{a} b . 2.3 . \log_{b} a = - 18$

Vậy P = -18.

Câu 15:

Tình giá trị của biểu thức $P = \log_{a} \frac{1}{b^{3}} \log_{\sqrt{b}} a^{3} (1 \neq a; b > 0)$

A. -18

B. $\frac{1}{2}$

C. 18

D. $\frac{1}{2}$

Xem đáp án

Đáp án A

Câu 16:

Tính giá trị của biểu thức $P = \log_{\sqrt{a}} b^{3} . \log_{\sqrt{b}} a (1 \neq a, b > 0)$

A. 3

B. 12

C. $\frac{3}{4}$

D. $\frac{4}{3}$

Xem đáp án

Chọn B

Ta có:

Câu 17:

Cho ln x= 2. Tính giá trị của biểu thức $T = 2 \ln \sqrt{e x} - \ln \frac{e^{2}}{\sqrt{x}} + \ln 3 . \log_{3} e x^{2}$

A. T = 21

B . T =12

C . T = 13

D. T =7

Xem đáp án

Chọn D

Câu 18:

Cho lnx= 3. Tính giá trị của biểu thức $T = 2 \ln \frac{x^{2}}{\sqrt{e}} + \ln 2 . \log_{2} (x^{3} . e^{2})$

A. T = 16

B . T = 15

C.T = $\frac{27}{2}$

D. T = 22

Xem đáp án

Chọn D

Ta có:

Câu 19:

Cho log_ab= 3 ; log_ac = -2. Tính giá trị của log_ax biết rằng $x = \frac{a^{2} b^{3}}{\sqrt{c^{5}}}$

A. 16

B. 6

C. 13

D. 3

Xem đáp án

Chọn A

Câu 20:

Cho log_ab= 2 ; log_ac= 3. Tính giá trị của biểu thức log_ax, biết rằng $x = \frac{a \sqrt{b^{3}}}{c^{2}}$

A. -6

B. -4

C. -2

D. -1

Xem đáp án

Chọn C

= 1+3/2.2-2.3= -2

Câu 21:

Cho các số thực dược a,b,c với a,b,ab $\neq 1$ . Khẳng định nào sau đây là sai.

A. $\log_{a} c + \log_{b} c = \log_{a b} c$

B. $2 \log_{a} b + 3 \log_{a} c = \log_{a} b^{2} . c^{3}$

C. $\log_{b} c + \log_{a} b = \log_{a} c$

D. $\log_{b} c = \frac{\log_{a} c}{\log_{a} b}$

Xem đáp án

Chọn C

+) Ta có: $\log_{c} a + \log_{c} b = \log_{c} a b$

$\Leftrightarrow \log_{c} a + \log_{c} b = \log_{c} a b$

$\Leftrightarrow \frac{1}{\log_{a} c} + \frac{1}{\log_{b} c} = \frac{1}{\log_{a b} c}$ . Suy ra A đúng.

+) Ta có: $2 \log_{a} b + 3 \log_{a} c = \log_{a} b^{2} + \log_{a} c^{3} = \log_{a} b^{2} . c^{3}$ . Suy ra B đúng

+) Ta có: $\log_{b} c = \frac{\log_{a} c}{\log_{a} b}$ ( do công thức). Suy ra D đúng

Câu 22:

Cho các số dương a; b và a≠ 1. Khẳng định nào dưới đây là sai

A.

B.

C.

D.

Xem đáp án

Chọn D.

Ta có:

Câu 23:

Cho các số dương a và b. Khẳng định nào dưới đây là sai.

A. $3^{\log_{a} b} = b^{\log_{a} 3}$

B. $a^{\log_{a} a b} = a b$

C. $a^{\log_{\sqrt{a}} b} = b^{2}$

D. $a^{\log_{a^{2}} b} = b^{2}$

Xem đáp án

Chọn D.

+) Ta có:

$3^{\log_{a} b} = b^{\log_{a} 3} \Leftrightarrow \log_{a} b = \log_{3} b^{\log_{a} 3} \Leftrightarrow \log_{a} b = \log_{a} 3 \log_{3} b \Leftrightarrow \log_{a} b = \log_{a} b (l u ô n đ ú n g)$