21 câu hỏi trắc nghiệm thuộc 200 câu trắc nghiệm Phương pháp tọa độ trong không gian nâng cao có đáp án (P8)

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;1;1). Viết phương trình mặt phẳng (P) đi qua M và cắt ba tia

Ox, Oy, Oz lần lượt tại các điểm A, B, C khác gốc O sao cho thể tích khối tứ diện OABC nhỏ nhất.

A. $2 x - y + 2 z - 3 = 0 .$

B. $4 x - y - z - 6 = 0$

C. $2 x + y + 2 z - 6 = 0$

D. $x + 2 y + 2 z - 6 = 0 .$

Xem đáp án

Chọn D

Gọi A (a;0;0), B (0;b;0), C (0;0;c), do A, B, C thuộc ba tia Ox, Oy, Oz nên a, b, c > 0.

Câu 2:

Trong không gian Oxyz, cho hai điểm M (2;2;1), $N (\frac{- 8}{3}; \frac{4}{3}; \frac{8}{3})$ . Viết phương trình mặt cầu có tâm là tâm của đường tròn nội tiếp tam giác OMN và tiếp xúc với mặt phẳng (Oxz).

A. x²+ (y+1)²+ (z+1)²=1.

B. x²+ (y-1)²+ (z-1)²=1

C. (x-1)²+ (y-1)²+z²=1

D. (x-1)²+y²+ (z-1)²=1.

Xem đáp án

Chọn B

Gọi I là tâm đường tròn nội tiếp tam giác OMN.

Ta áp dụng tính chất sau: “Cho tam giác OMN với I là tâm đường tròn nội tiếp, ta có

với a = MN, b = ON, c = OM.

Ta có:

Mặt phẳng (Oxz) có phương trình y = 0.

Mặt cầu tiếp xúc với mặt phẳng (Oxz) nên mặt cầu có bán kính R = d (I, (Oxz)) = 1.

Vậy phương trình mặt cầu là x²+ (y-1)²+ (z-1)²=1.

Câu 3:

Trong không gian Oxyz, Cho mặt phẳng (R): x+y-2z+2=0 và đường thẳng $∆_{1} : \frac{x}{2} = \frac{y}{1} = \frac{z - 1}{- 1}$ .Đường thẳng Δ₂ nằm trong mặt phẳng (R) đồng thời cắt và vuông góc với đường thẳng Δ₁ có phương trình là:

A. $\{\begin{cases} x = t \\ y = - 3 t \\ z = 1 - t \end{cases}$

B. $\{\begin{cases} x = t \\ y = - 2 t \\ z = 1 + t \end{cases}$

C. $\{\begin{cases} x = 2 + t \\ y = 1 - t \\ z = t \end{cases}$

D. $\{\begin{cases} x = 2 + 3 t \\ y = 1 - t \\ z = t \end{cases}$

Xem đáp án

Chọn A

Phương trình tham số của đường thẳng Δ₁ là

Gọi I (x;y;z) là giao điểm của Δ₁ và (R).

Khi đó tọa độ của I là thỏa mãn:

Mặt phẳng (R) có VTPT

;

Đường thẳng Δ₁ có VTCP

.

Đường thẳng Δ₂ nằm trong mặt phẳng (R) đồng thời cắt và vuông góc với đường thẳng Δ₁.

Do đó Δ₂ đi qua I = (0;0;1) và nhận $[\vec{n}, \vec{u}]$ làm một VTCP.

Vậy phương trình của Δ₂ là

Câu 4:

Trong không gian Oxyz, mặt phẳng (α) đi qua M (1;1;4) cắt các tia Ox, Oy, Oz lần lượt tại A, B, C phân biệt sao cho tứ diện OABC có thể tích nhỏ nhất. Tính thể tích nhỏ nhất đó.

A. 72.

B. 108

B. 18.

D. 36.

Xem đáp án

Chọn B

Đặt A= (a;0;0), B= (0;b;0), C= (0;0;c) với a, b, c>0.

Khi đó phương trình mặt phẳng (α) là

Vì (α) đi qua M (1;1;4) nên

Thể tích của tứ diện OABC là

Áp dụng bất đẳng thức AM - GM ta có

Dấu bằng xảy ra khi $a = b = 3; c = 12 .$

Vậy tứ diện OABC có thể tích nhỏ nhất bằng

Câu 5:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 1}{1} = \frac{y}{- 1} = \frac{z - 2}{1}$ và mặt phẳng (P): 2x-y-2z+1=0. Đường thẳng nằm trong (P), cắt và vuông góc với d có phương trình là:

A. $\frac{x + 2}{3} = \frac{y - 1}{4} = \frac{z + 3}{1}$

B. $\frac{x - 2}{3} = \frac{y + 1}{4} = \frac{z - 3}{- 1}$

C. $\frac{x - 2}{3} = \frac{y + 1}{4} = \frac{z - 3}{1}$

D. $\frac{x - 1}{3} = \frac{y + 1}{4} = \frac{z - 1}{1}$

Xem đáp án

Chọn C

Phương trình tham số của

.

Gọi M = d ∩ (P).

Khi đó M ∈ d nên M (1+t;-t;2+t) ; M ∈ (P) nên 2(1 + t) – (- t) – 2 (2 + t) + 1 = 0 có t = 1.

Vậy đường thẳng d cắt mặt phẳng (P) tại M (2;-1;3).

Gọi

lần lượt là vectơ chỉ phương của d và vectơ pháp tuyến của mặt phẳng (P).

Khi đó một vectơ chỉ phương của đường thẳng cần tìm là

.

Vậy phương trình đường thẳng cần tìm là

Câu 6:

Có bao nhiêu mặt cầu (S) có tâm thuộc đường thẳng $∆ : \frac{x - 3}{2} = \frac{y - 1}{- 1} = \frac{z - 1}{- 2}$ đồng thời tiếp xúc với hai mặt phẳng (α₁): $2 x + 2 y + z - 6 = 0$ và (α₂): $x - 2 y + 2 z = 0$

A. 1

B. 0.

C. Vô số

D. 2.

Xem đáp án

Chọn C

Phương trình tham số của đường thẳng Δ:

Gọi tâm I ∈ Δ $\Rightarrow$ I (3+2t;1-t;1-2t)

Vì mặt cầu (S) đồng thời tiếp xúc với hai mặt phẳng (α₁) và (α₂) nên ta có

Do đó có vô số mặt cầu thỏa yêu cầu đề bài.

Câu 7:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;0;1), B (0;1;-1). Hai điểm D, E thay đổi trên các đoạn OA, OB sao cho đường thẳng DE chia tam giác OAB thành hai phần có diện tích bằng nhau. Khi DE ngắn nhất thì trung điểm của đoạn DE có tọa độ là:

A. $I (\frac{\sqrt{2}}{4}; \frac{\sqrt{2}}{4}; 0)$

B. $I (\frac{\sqrt{2}}{3}; \frac{\sqrt{2}}{3}; 0)$

C. $I (\frac{1}{3}; \frac{1}{3}; 0)$

D. $I (\frac{1}{4}; \frac{1}{4}; 0)$

Xem đáp án

Dấu bằng xảy ra khi và chỉ khi OD = OE = 1

Chú ý: Sau khi chứng minh được OD=OE=1 thì ta có thể tìm trung điểm I của DE như sau:

Câu 8:

Trong hệ tọa độ Oxyz cho A (3;3;0), B (3;0;3), C (0;3;3). Mặt phẳng (P) đi qua O, vuông góc với mặt phẳng (ABC)

sao cho mặt phẳng (P) cắt các cạnh AB, AC tại các điểm M, N thỏa mãn thể tích tứ diện OAMN nhỏ nhất. Mặt phẳng (P) có phương trình:

A. $x + y - 2 z = 0 .$

B. $x + y + 2 z = 0 .$

C. $x - z = 0 .$

D. $y - z = 0$

Xem đáp án

Chọn A

Nhận thấy tam giác ABC đều có trọng tâm G (2;2;2), và OG ⊥ (ABC) nên hình chiếu của O lên (ABC) là điểm G

Vì OG và

cố định nên thể tích V_OAMNnhỏ nhất khi và chỉ khi AM. AN nhỏ nhất.

Vì M, N, G thẳng hàng nên

,

suy ra

.

Đẳng thức xảy ra khi

.

Khi đó mặt phẳng (P) đi qua O và nhận

là một vectơ pháp tuyến, do đó (P): $x + y - 2 z = 0 .$

Câu 9:

Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9, điểm A (0; 0; 2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là:

A. (P): $x + 2 y + 3 z + 6 = 0 .$

B. (P): $x + 2 y + z - 2 = 0 .$

C. (P): $x - 2 y + z - 6 = 0 .$

D. (P): $3 x + 2 y + 2 z - 4 = 0 .$

Xem đáp án

Chọn B

Mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 có tâm I (1;2;3), bán kính R=3.

IA = √6 < R nên A nằm trong mặt cầu.

Gọi r là bán kính đường tròn thiết diện, ta có

Trong đó h là khoảng cách từ I đến (P).

Diện tích thiết diện là

Vậy diện tích hình tròn (C) đạt nhỏ nhất khi h = IA. Khi đó $\vec{I A}$ là véc tơ pháp tuyến của (P).

Phương trình mặt phẳng (P) là 1 $(x - 0) + 2 (y - 0) + (z - 2) = 0 c ó x + 2 y + z - 2 = 0$

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho các điểm A (2;0;0), B (0;3;0), C (0;0;6), D (1;1;1). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D?

A. 6

B. 10

C. 7

D. 5.

Xem đáp án

Chọn C

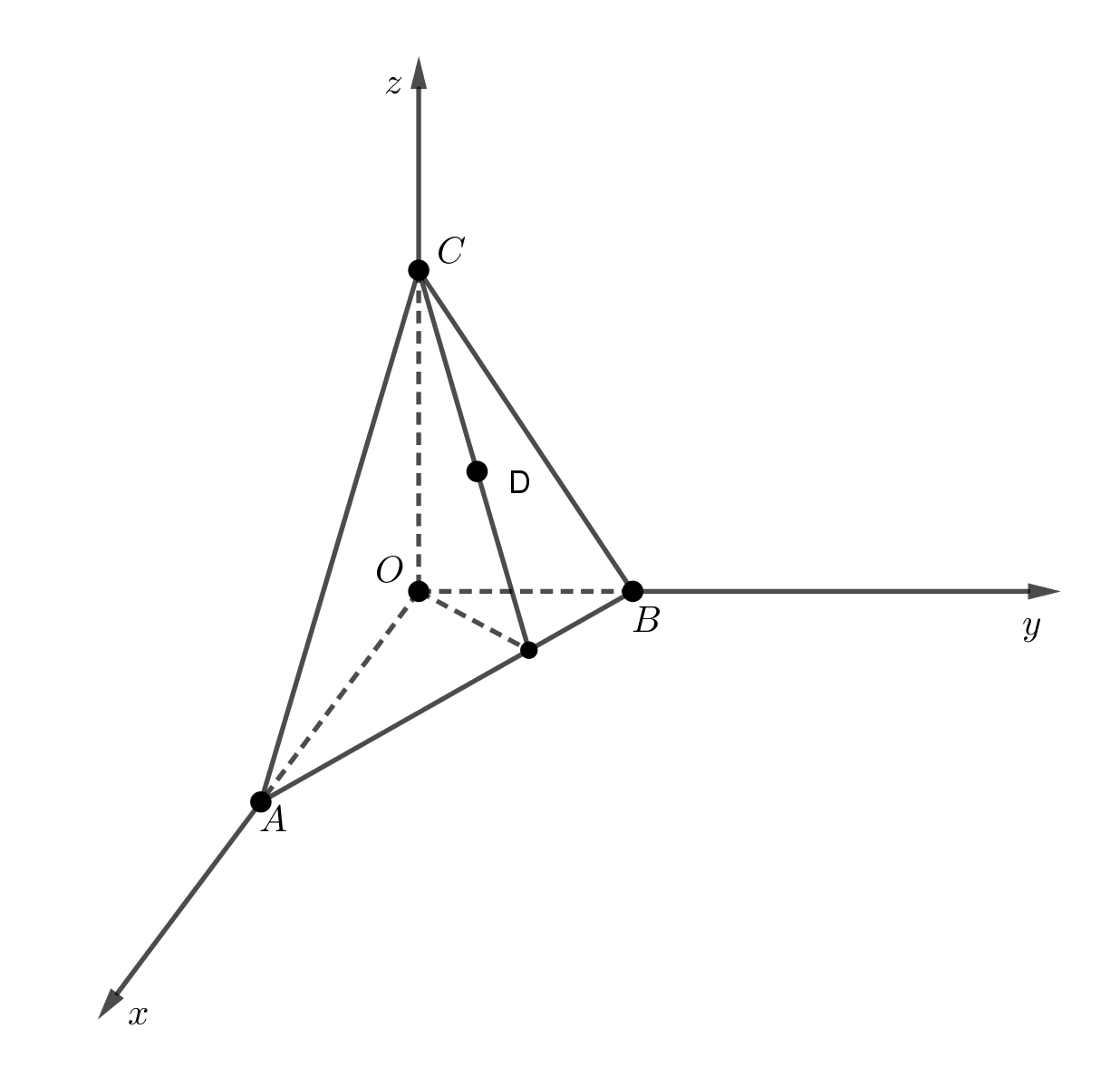
Phương trình mặt phẳng

Ta thấy 4 điểm A, B, C, D đồng phẳng (do D ∈ (ABC)).

Chọn 3 trong 5 điểm có

Chọn 3 trong 4 điểm đồng phẳng A, B, C, D có

Vậy có 10 - 4 + 1 = 7 $\Rightarrow$ mặt phẳng phân biệt đi qua 5 điểm đã cho.

Câu 11:

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A (1;1;0), B (0;-1;2). Biết rằng có hai mặt phẳng cùng đi qua hai điểm A, O và cùng cách B một khoảng bằng $\sqrt{3}$ . Véctơ nào trong các véctơ dưới đây là một véctơ pháp tuyến của một trong hai mặt phẳng đó.

A. $\vec{n} = (1; - 1; - 1)$

B. $\vec{n} = (1; - 1; - 3)$

C. $\vec{n} = (1; - 1; 5)$

D. $\vec{n} = (1; - 1; - 5)$

Xem đáp án

Chọn D

Phương trình đường thẳng qua hai điểm A, O có dạng

Gọi (P) là mặt phẳng cùng đi qua hai điểm A, O nên (P): $a (x - y) + b z = 0, a ² + b ² > 0$ . Khi đó véctơ pháp tuyến của (P) có dạng $\vec{n} (a; - a; b)$

Ta có: $d (B; (P)) = \sqrt{3} \Leftrightarrow \frac{|a + 2 b|}{\sqrt{a^{2} + a^{2} + b^{2}}} = \sqrt{3} \Leftrightarrow 5 a^{2} - 4 a b - b^{2} = 0 \Leftrightarrow [\begin{matrix} \frac{a}{b} = 1 \Rightarrow a = b \\ \frac{a}{b} = - \frac{1}{5} \Rightarrow b = - 5 a \end{matrix}$

Với a = b thì VTPT của một trong hai mặt phẳng là: $\vec{n} = (a; - a; a) = a (1; - 1; 1)$

Với b = -5a thì VTPT của một trong hai mặt phẳng là: $\vec{n} = (a; - a; - 5 a) = a (1; - 1; - 5)$

Câu 12:

Trong không gian với hệ tọa độ Oxy, cho mặt phẳng (P): $2 y - z + 3 = 0$ và điểm A (2;0;0). Mặt phẳng (α) đi qua A, vuông góc với (P), cách gốc tọa độ O một khoảng bằng $\frac{4}{3}$ và cắt các tia Oy, Oz lần lượt tại các điểm B, C khác O. Thể tích khối tứ diện OABC bằng:

A. 8.

B. 16

C. $\frac{8}{3}$

D. $\frac{16}{3}$

Xem đáp án

Chọn C

Giả sử B (0;b;0) và C (0;0;c), với b, c > 0.

Khi đó phương trình mặt phẳng (α) là:

Câu 13:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x + 1}{2} = \frac{y - 1}{1} = \frac{z - 2}{3}$ và mặt phẳng (P): $x - y - z - 1 = 0$ . Phương trình đường thẳng Δ đi qua A (1;1;-2), song song với mặt phẳng (P) và vuông góc với đường thẳng d là:

A. $△ : \frac{x + 1}{2} = \frac{y + 1}{5} = \frac{z - 2}{- 3}$

B. $△ : \frac{x - 1}{2} = \frac{y - 1}{5} = \frac{z + 2}{- 3}$

C. $△ : \frac{x + 1}{- 2} = \frac{y + 1}{- 5} = \frac{z - 2}{3}$

D. $△ : \frac{x - 1}{- 2} = \frac{y - 1}{- 5} = \frac{z + 2}{3}$

Xem đáp án

Chọn B

Ta có VTCP của đường thẳng d là: $\vec{u_{d}} (2; 1; 3)$

VTPT của mặt phẳng (P) là: $\vec{n_{(P)}} (1; - 1; - 1)$

Vì $\{\begin{cases} ∆ ⊥ d \\ ∆ ⊥ (P) \end{cases} \Rightarrow \vec{u_{∆}} = [\vec{u_{d}}; \vec{n_{(P)}}] = (2; 5; - 3)$

Δ có vectơ chỉ phương $\vec{u_{∆}} = (2; 5; - 3)$ và đi qua A (1;1;-2) nên có phương trình:

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;0;-1) và mặt phẳng (P): x+y-z-3=0. Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng $\frac{\sqrt{17}}{2}$ . Tính bán kính R của mặt cầu (S).

A. R=3.

B. R=9

C. R=1

D. R=5.

Xem đáp án

Chọn A

Gọi I (a;b;c)

Ta có IA=IO=R ó hình chiếu của I lên OA là trung điểm

của OA.

Theo bài ra ta có:

Câu 15:

Cho hình chóp S. ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng a $\sqrt{2}$ và SA vuông góc với mặt phẳng (ABCD). Gọi α là góc giữa hai mặt phẳng (SBD) và (ABCD). Nếu tan α = $\sqrt{2}$ thì góc giữa hai mặt phẳng (SAC) và (SBC) bằng:

A. 300

B. 600

C. 450

D. 900

Xem đáp án

Hình vuông ABCD có độ dài đường chéo bằng $a \sqrt{2}$ suy ra hình vuông đó có cạnh bằng a.

Chọn hệ trục tọa độ Oxyz như hình vẽ. Ta có A (0;0;0), B (a;0;0), C (a;a;0), S (0;0;a).

Câu 16:

Trong không gian Oxyz, cho đường thẳng và mặt phẳng (P): $2 x - y + 2 z + 1 = 0$ . Đường thẳng $d : \frac{x + 2}{4} = \frac{y - 1}{- 4} = \frac{z + 2}{3}$ Tính T = m² - n².

A. T = -5.

B. T = 4.

C. T = 3

D. T = -4.

Xem đáp án

Chọn D

Mặt phẳng (P) có vec tơ pháp tuyến

và đường thẳng d có vec tơ chỉ phương

Vì Δ song song với mặt phẳng (P) nên

Mặt khác ta có

Xét hàm số

Dựa vào bảng biến thiên ta có max f(t) = f (0) = 5 suy ra $(\hat{∆}; d)$ bé nhất khi $m = 0 \Rightarrow n = 2 .$ Do đó T = m² - n² = -4.

Làm theo cách này thì không cần đến dữ kiện: đường thẳng Δ đi qua E (-2;1;-2).

Câu 17:

Trong không gian Oxyz, cho các điểm A, B, C (không trùng O) lần lượt thay đổi trên các trục Ox, Oy, Oz và luôn thỏa mãn điều kiện: tỉ số giữa diện tích của tam giác ABC và thể tích khối tứ diện OABC bằng 3/2. Biết rằng mặt phẳng (ABC) luôn tiếp xúc với một mặt cầu cố định, bán kính của mặt cầu đó bằng:

A. 3.

B. 2.

C. 4.

D. 1.

Xem đáp án

Vậy mặt phẳng (ABC) luôn tiếp xúc mặt cầu tâm O, bán kính R = 2.

Câu 18:

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có phương trình đường phân giác trong góc A là: $\frac{x}{1} = \frac{y - 6}{- 4} = \frac{z - 6}{- 3}$ . Biết rằng điểm M (0;5;3) thuộc đường thẳng AB và điểm N (1;1;0) thuộc đường thẳng AC. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng AC.

A. $\vec{u} = (1, 2, 3)$

B. $\vec{u} = (0, 1, 3)$

C. $\vec{u} = (0, - 2, 6)$

D. $\vec{u} = (0, 1, - 3)$

Xem đáp án

Chọn B

Phương trình tham số của đường phân giác trong góc

Gọi D là điểm đối xứng với M qua (d). Khi đó D ∈ AC $\Rightarrow$ đường thẳng AC có một vectơ chỉ phương là $\vec{N D}$ .

Ta xác định điểm D.

Gọi K là giao điểm MD với (d). Ta có K $(t; 6 - 4 t; 6 - 3 t);$

Câu 19:

Trong không gian Oxyz, phương trình mặt phẳng (P) song song và cách đều hai đường thẳng $d_{1} : \frac{x - 2}{- 1} = \frac{y}{1} = \frac{z}{1}$ , $d_{2} : \frac{x}{2} = \frac{y - 1}{- 1} = \frac{z - 2}{- 1}$ là?

A. (P): $2 y - 2 z + 1 = 0 .$

B. (P): $2 x - 2 z + 1 = 0 .$

C. (P): $2 x - 2 y + 1 = 0 .$

D. (P): $2 y - 2 z - 1 = 0 .$

Xem đáp án

Chọn A

Mặt phẳng (P) song song và cách đều hai đường thẳng

và nên:

(P) có một véc tơ pháp tuyến là

suy ra (P):y-z+D=0

Và d (A, (P))=d (B, (P)) có |D| = |D – 1| $\Rightarrow D = \frac{1}{2}$

Vậy (P): $2 y - 2 z + 1 = 0 .$

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho điểm A (3;1;0), B (-9;4;9) và mặt phẳng (P) có phương trình $2 x - y + z + 1 = 0 .$ Gọi I (a;b;c) là điểm thuộc mặt phẳng (P) sao cho |IA - IB| đạt giá trị lớn nhất. Khi đó tổng a+b+c bằng:

A. $- 4$

B. 22

C. 13.

D. $- 13 .$

Xem đáp án

Chọn A

Thay tọa độ hai điểm A (3;1;0), B (-9;4;9) vào vế trái phương trình mặt phẳng (P), ta có

$2 . 3 - 1 + 0 + 1 = 6 > 0$ và $2 . (- 9) - 4 + 9 + 1 = - 12 < 0 .$

Nên suy ra, hai điểm A, B nằm khác phía với mặt phẳng (P).

Gọi A' là điểm đối xứng với điểm A qua mặt phẳng (P). Khi đó:

+) Phương trình đường thẳng AA' nhận VTPT của mặt phẳng (P) là VTCP và đi qua điểm A(3;1;0) là:

$\{\begin{cases} x = 3 + 2 t \\ y = 1 - t \\ z = t \end{cases}$

+) Gọi H(3+2t;1-t;t) là giao điểm của AA' và mặt phẳng (P). Khi đó tọa độ điểm H thỏa mãn:

2(3+2t) - (1-t) + t +1 =0

$\Leftrightarrow 6 + 6 t = 0 \Leftrightarrow t = - 1 \Rightarrow H (1; 2; - 1)$

+) Vì H là trung điểm của AA' nên $\Rightarrow A' (- 1; 3; - 2)$

+) Xét $∆ I A' B$ ta có:

(bất đẳng thức trong tam giác)

Dấu “=” xảy ra khi và chỉ khi A', B, I thẳng hàng và I nằm ngoài đoạn A'B. Suy ra I là giao điểm của đường thẳng A'B và mặt phẳng (P).

Ta có

,

nên suy ra phương trình đường thẳng A'B là

.

Tọa độ điểm I là nghiệm của hệ phương trình

Vậy I (7;2;13) nên $a + b + c = 7 + 2 + (- 13) = - 4 .$

Câu 21:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+y²+ (z+2)²=4 và đường thẳng $d : \{\begin{cases} x = 2 - y y = t \\ z = m - 1 + t \end{cases}$ . Gọi T là tập tất cả các giá trị của m để d cắt (S) tại hai điểm phân biệt A, B sao cho các tiếp diện của (S) tại A và B tạo với nhau góc lớn nhất có thể. Tính tổng các phần tử của tập hợp T.