Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 3
-
2029 lượt thi
-
50 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
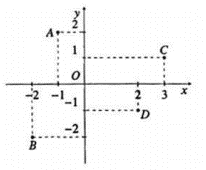
Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức z = ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
z = = = −1 + 2i
Điểm biểu diễn của số phức z = −1 + 2i là điểm A
Câu 2:
Trong không gian Oxyz, cho mặt cầu (S) : x2 + y2 + z2 + 2x + 4y – 6z – 1 = 0. Tâm của mặt cầu (S) có tọa độ là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tâm của mặt cầu (S) là (−1; −2; 3)
Câu 4:
Cho hai số phức z1 = 2 + 3i, z2 = −4 – i. Số phức z = z1 – z2 có môđun là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
z = z1 – z2 = (2 + 3i) – (−4 – i) = 6 + 4i
|z| = =
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Thể tích khối tròn xoay được tạo thành là V = π
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
= f(b) – f(a)
Câu 7:
Cho biết F(x) là một nguyên hàm của hàm số f(x). Biểu thức bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Do F(x) là nguyên hàm của f(x) nên = F(x) + C
Câu 8:
Trong không gian với hệ trục tọa độ Oxyz, cho = −2 + 4 − 6. Tọa độ của bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tọa độ của = (−2; 4; −6)
Câu 9:
Trong không gian Oxyz, cho đường thẳng d có phương trình (t ∈ ℝ). Hỏi đường thẳng d đi qua điểm nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Thay lần lượt các điểm C, B, D, A vào phương trình đường thẳng d có:
+) Điểm C: (vô lí);
+) Điểm B: (thỏa mãn);
+) Điểm D: (vô lí);
+) Điểm A: (vô lí);
Vậy đường thẳng d đi qua điểm B(2; 3; −2).
Câu 10:
Cho hàm số f(x) = . Trong các khẳng định sau, khẳng định nào đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
= tanx + C
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
(S) có tâm I(−1; 1; −2) và r = 3 có phương trình là:
(x + 1)2 + (y – 1)2 + (z + 2)2 = 9
Câu 12:
Tất cả các nghiệm phức của phương trình z2 – 2z + 17 = 0 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
z2 – 2z + 17 = 0 Û
Câu 13:
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có vectơ pháp tuyến và . Gọi φ là góc giữa hai mặt phẳng (P) và (Q). Chọn công thức đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
φ là góc giữa hai mặt phẳng (P) và (Q) là: cos φ = .
Câu 14:
Trong không gian Oxyz, cho phương trình mặt phẳng (P) : 2x – z + 2 = 0. Một vectơ pháp tuyến của mặt phẳng (P) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vectơ pháp tuyến của (P) là (2; 0; −1)
Câu 15:
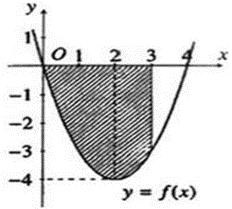
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới. Diện tích S của miền được tô đậm như hình vẽ được tính theo công thức nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Diện tích của miền tô đậm là: S =
Câu 16:
Cho số phức z = −1 + 5i. Phần ảo của số phức bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
= −1 – 5i nên phần ảo là −5
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: |z| = || =
Câu 18:
Trong không gian Oxyz, cho ba điểm A(2; 0; 0), B(0; 3; 0) và C(0; 0; 5). Mặt phẳng (ABC) có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Phương trình mặt phẳng (ABC) là:
Câu 19:
Trong không gian Oxyz, cho mặt phẳng (P): 2x – 2y + z + 6 = 0. Khoảng cách từ gốc tọa độ đến mặt phẳng (P) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Khoảng cách từ gốc tọa độ đến mặt phẳng (P) bằng:
d(O; (P)) = = = 2.
Câu 20:
Trong không gian Oxyz, cho mặt phẳng (α) : 2x – 3y + z – 3 = 0. Mặt phẳng nào dưới đây song song với mặt phẳng (α)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Do mặt phẳng cần tìm song song với (α) nên có cùng vectơ pháp tuyến = (2; −3; 1)
Mặt phẳng cần tìm là : (γ) : 2x – 3y + z + 2 = 0
Câu 21:
Trong không gian Oxyz, gọi M(a; b; c) là giao điểm của đường thẳng d : và mặt phẳng (P) : 2x + 3y – 4z + 4 = 0. Tính T = a + b + c
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
d:
Phương trình hoành độ giao điểm giữa d và (P), thay d vào (P) được:
−2 + 4t + 9 – 3t – 8 – 4t + 4 = 0 Û 3t = 3 Û t = 1
Thay t = 1 vào d ta được M(1; 2; 3)
Nên T = 1 + 2 + 3 = 6
Câu 22:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm I(2; 0; −2) và A(2; 3; 2). Mặt cầu (S) có tâm I và đi qua điểm A có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
= (0; 3; 4)
IA = = 5 = R
Phương trình mặt cầu (S) có R = 5 có phương trình là:
(x – 2)2 + y2 + (z + 2)2 = 25
Câu 23:
Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z thỏa mãn điều kiện |z – i + 2| = 2 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Theo đề bài: z thỏa mãn |z – (a + bi)| = R có tập hợp điểm là đường tròn tâm I(a; b), bán kính R.
Nên |z – i + 2| = 2 là đường tròn tâm I(−2; 1) và R = 2.
Câu 24:
Trong không gian với hệ tọa độ Oxyz, cho điểm M(−2; 1; 8). Gọi H là hình chiếu vuông góc của M trên mặt phẳng (Oxy). Tọa độ của điểm H là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Hình chiếu vuông góc của M là H(−2; 1; 0)
Câu 25:
Gọi S là diện tích hình phẳng giới hạn bởi hai đường y = và y = 4 – x. Tính S
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Phương trình hoành độ giao điểm là: = 4 – x Û x(4 – x) = 3 Û −x2 + 4x – 3 = 0
Û
Diện tích giới hạn bởi 2 đường thẳng là:
S = = .
Câu 27:
Trong không gian Oxyz, cho phương trình của hai đường thẳng d1 : và d2 : . Vị trí tương đối của hai đường d1 và d2 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
d1 có = (2; −1; 1)
d2 có = (1; 1; −2)
[] = (1; 5; 3)
M1 (0; 0; 1) ∈ d1; M2 (3; 0; 0) ∈ d2
Þ = (3; 0; −1)
|[] . | = 0
Mà và không cùng phương (≠ 0) nên d1 và d2 cắt nhau
Câu 28:
Giá trị các số thực a, b thỏa mãn 2a + (b + 1 + i)i = 1 + 2i (với i là đơn vị ảo) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
2a + (b + 1 + i)i = 1 + 2i Û 2a + bi + i – 1 = 1 + 2i Û (2a – 1) + (b + 1)i = 1 + 2i
Ta có: Û
Câu 30:
Gọi z1, z2 là hai nghiệm phân biệt của phương trình z2 + 3z + 4 = 0 trên tập số phức. Tính giá trị của biểu thức P = |z1| + |z2|
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
z2 + 3x + 4 = 0 Û
|z1| = = 2
|z2| = = 2
Vậy P = 2 + 2 = 4
Câu 32:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
(2 – i)z + 3i + 2 = 0 Û z = = = =
Vậy phần thực của số phức là
Câu 33:
Trong không gian với hệ tọa độ Oxyz, đường thẳng đi qua hai điểm A(3; 1; −6) và B(5; 3; −2) có phương trình tham số là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
= (2; 2; 4) = (1; 1; 2)
Phương trình tham số của đường thẳng đi qua điểm B và có vectơ chỉ phương là:
Câu 34:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2; 1; 1), B(−1; 2; 1). Tọa độ trung điểm của đoạn thẳng AB là?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi tọa độ trung điểm của AB là I
I có tọa độ : Û Þ I
Câu 35:
Trong không gian hệ tọa độ Oxyz, cho mặt phẳng (α) : 2x + 2y – z – 6 = 0. Gọi mặt phẳng (β) : x + y + cz + d = 0 không qua O, song song với mặt phẳng (α) và d((α),(β)) = 2. Tính c.d?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Do (α) // (β) nên Þ c =
Þ (β) : x + y z + d = 0
(α) : 2x + 2y – z – 6 = 0 Û x + y − z − 3 = 0
d((α);(β)) = 2 Û Û |3 + d| = 3 Û
Vì (β) không đi qua O nên loại d = 0
Nên d = −6
Vậy c.d = .(−6) = 3
Câu 37:
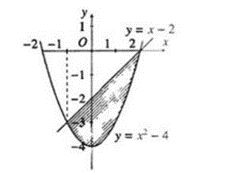
Tính diện tích hình phẳng (phần được tô đậm) giới hạn bởi hai đường thẳng y = x2 – 4; y = x – 2 như hình vẽ bên dưới là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Phương trình hoành độ giao điểm là: x2 – 4 = x – 2 Û x2 – x – 2 = 0 Û
Diện tích hình phẳng là: S = = .
Câu 38:
Trong không gian, cắt vật thể bởi hai mặt phẳng (P) : x = −1 và (Q) : x = 2. Biết một mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (−1 ≤ x ≤ 2) cắt theo thiết diện là một hình vuông có cạnh bằng 6 – x. Thể tích của vật thể giới hạn bởi hai đường thẳng (P), (Q) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
V = = = 93π.
Câu 39:
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(2; 2; 2), B(0; 1; 1) và C(−1; −2; −3). Tính diện tích S của tam giác ABC
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: = (−2; −1; −1); = (−3; −4; −5)
Diện tích ∆ABC là: S = = =
Vậy S = .
Câu 40:
Cho = với a, b, c là các số nguyên, c < 0 và tối giản. Tổng a + b + c bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: cos4x . cosx = (cos 3x + cos5x)
Nên I = =
= = ![]()
Nên a = 30; b = 13; c = −60
Vậy a + b + c = 30 + 13 – 60 = −17
Câu 41:
Trong không gian Oxyz, mặt phẳng (α) đi qua hai điểm A(1; 0; 0), B(2; 2; 0) và vuông góc với mặt phẳng (P) : x + y + z – 2 = 0 có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
(P) có = (1; 1; 1)
= = (−2; 1; 1)
Phương trình mặt phẳn (α) đi qua A(1; 0; 0) và có là:
−2x + y + z + 2 = 0 Û 2x – y – z – 2 = 0
Vậy (α) : 2x – y – z – 2 = 0
Câu 42:
Tính nguyên hàm bằng cách đặt t = lnx ta được nguyên hàm nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đặt t = lnx Û dt = dx
Do đó, ta có : =
Câu 43:
Trong không gian với hệ tọa độ Oxyz, cho (S) : x2 + y2 + z2 – 4x – 2y + 10z – 14 = 0. Mặt phẳng (P) : −x + 4z + 5 = 0 cắt mặt cầu (S) theo một đường tròn (C). Tọa độ tâm H của (C) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
(S) : (x – 2)2 + (y – 1)2 + (z + 5)2 = 44
Þ Tâm I(2; 1; −5)
H là hình chiếu của I lên (P)
(P) có = (−1; 0; 4)
d đi qua M và vuông góc với (P) có phương trình :
Þ H ∈ d nên H(2 – t; 1; −5 + 4t)
H ∈ (P) Û −(2 – t) + 4(−5 + 4t) + 5 = 0 Û t = 1
Þ H(1;1; −1)
Vậy H(1; 1; −1)
Câu 44:
Biết phương trình z2 + mz + n = 0 (m; n ∈ ℝ) có một nghiệm là 1 – 3i. Tính n + 3m
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì 1 – 3i là nghiệm của số phức nên
(1 – 3i)2 + m(1 – 3i) + n = 0
Û −8 – 6i + m – 3mi + n = 0
Û Û
Vậy 3m + n = 10 – 6 = 4
Câu 45:
Cho số phức z = x + iy (với x; y ∈ ℝ) thỏa mãn: 2z – 5i. = −14 – 7i. Tính x + y
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
z = x + iy Û = x – iy
2z – 5i. = −14 – 7i
Û 2(x + iy) – 5i(x – iy) = −14 – 7i
Û 2x + 2yi – 5ix + 5i2y = −14 − 7i
Û (2x – 5y) + (2y – 5x)i = −14 – 7i
Û Û
Nên x + y = 3 + 4 = 7
Câu 46:
Cho hàm số f(x) = ax3 + bx2 – 36x + c (a≠ 0; a, b, c ∈ ℝ) có hai điểm cực trị là −6 và 2. Gọi y = g(x) là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = f(x). Diện tích hình phẳng giới hạn bởi hai đường thẳng y = f(x) và y = g(x) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
f '(x) = 3ax2 + 2bx – 36
Vì f '(x) có 2 điểm cực trị là −6 và 2 nên:
Û
Ta được: f(x) = x3 + 6x2 – 36x + c
Tại x = −6 : f(−6) = −216 + 216 + 216 + c = 216 + c
Tại x = 2 : f(2) = 8 + 24 – 72 + c = −40 + c
g(x) = a’x + b’ đi qua 2 điểm cực trị của f(x) nên :
Û
Û 216 + c + 6a’ = −40 + c – 2a’ Þ 256 = −8a’ Þ a’ = −32 Þ b = 24 + c
g(x) = −32x + 24 + c
f(x) = g(x) Û x3 + 6x2 – 36x + c = −32x + 24 + c
Û
Do đó S = = 128
Vậy S = 128
Câu 47:
Trong không gian với hệ tọa độ Oxyz, gọi mặt phẳng (P) : 7x + by + cz + d = 0 (với b, c, d ∈ ℝ; c <0) đi qua điểm A(1; 3; 5). Biết mặt phẳng (P) song song với trục Oy và khoảng cách từ gốc tọa độ đến mặt phẳng (P) bằng . Tính T = b + c + d.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
A ∈ (P) : 7.1 + b.3 + c.5 + d = 0 Û 3b + 5c + d = 0
Oy có vectơ chỉ phương = (0; 1; 0)
(P) // Oy Þ . = 0 Þ b = 0 nên ta có : 5c + d = −7 Û d = −7 – 5c
d(O; (P)) = =
Û =
Û |5c + 7| = .
Û (5c + 7)2 = 18(c2 + 49)
Û 25c2 + 70c + 49 = 18c2 + 882
Û 7c2 + 70c – 833 = 0
Û Û
Þ b + c + d =
Vậy T = b + c + d = 61.
Câu 48:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(−2; −2; 1), A(1; 2; −3) và đường thẳng d : . Gọi = (1; a; b) là một vectơ chỉ phương của đường thẳng ∆ đi qua M, ∆ vuông góc với đường thẳng d đồng thời cách điểm A một khoảng nhỏ nhất. Giá trị của a + 2b là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
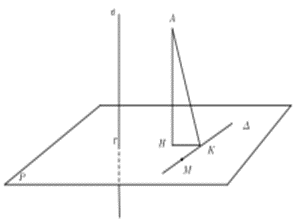
Gọi (P) là mặt phẳng đi qua M và vuông góc với d, khi đó (P) chứa ∆
Mặt phẳng (P) qua M(−2; −2; 1) và có vectơ pháp tuyến = = (2; 2; −1) nên có phương trình : (P) : 2x + 2y – z + 9 = 0
Gọi H, K lần lượt là hình chiếu của A lên (P) và ∆. Khi đó: AK ≥ AH nên AK min khi
K ≡ H. Đường thẳng AH đi qua A(1; 2; −3) và có vectơ chỉ phương = (2; 2; −1) nên AH có phương trình tham số:
H ∈ AH Þ H(1 + 2t; 2 + 2t; −3 – t)
H ∈ (P) Þ 2(1 + 2t) + 2(2 + 2t) –(−3 – t) + 9 = 0 Þ H(−3; −2; −1)
Nên = = (1; 0; 2)
Vậy a = 0; b = 2 Þ a + 2b = 4
Câu 49:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đặt z1 = a + bi (a, b ∈ ℝ), z2 = c + di
Ta có : =
Û |z| − = a + bi − =
Theo bài ta có: |z| − = Û |z| = 4
|z1 – z2| = 3 Û (a – c)2 + (b – d)2 = 9
Û a2 + b2 + c2 + d2 – 2(ac + bd) = 9
Û ac + bd = −1
|z1 + 2z2| =
= = .
Theo tính chất |z + z'| ≤ |z| + |z'| ta có:
|z1 + 2z2− 3i| ≥ |z1 + 2z2| + |−3i| = −
Vậy giá trị nhỏ nhất là 3 −
Câu 50:
Cho hàm số y = f(x) là hàm liên tục có tích phân trên [0; 2] thỏa mãn điều kiện f(x2) = 6x4 + . Tính I =
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đặt = m Û f(x2) = 6x4 + m Þ f(x) = 6x2 + m
Do đó ta được: = m
Û = m Û 24 + 2m = m Û m = −12
Nên I = = = −8
Vậy I = −8.
