Trắc nghiệm Số phức có đáp án (Vận dụng)
-
1245 lượt thi
-
15 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 2:
Cho ba điểm A, B, C lần lượt biểu diễn các số phức sau . Tìm các giá trị thực của m sao cho tam giác ABC vuông tại B.
 Xem đáp án
Xem đáp án
Ta có:
Có và
Đáp án cần chọn là: A
Câu 3:
Cho số phức z. Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Giả sử
Lại có:
Do đó
Đáp án cần chọn là: B
Câu 4:
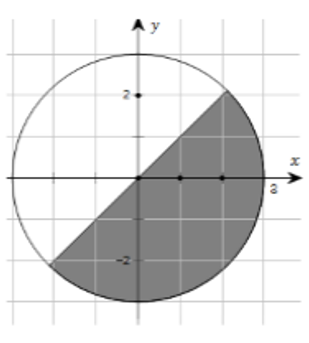
Gọi M là điểm biểu diễn của số phức z, biết tập hợp các điểm M là phần tô đậm ở hình bên (kể cả biên). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Gọi và biểu diễn z trên mặt phẳng tọa độ
Từ hình vẽ ta có:
Đáp án cần chọn là: B
Câu 5:
Cho các số phức và có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm A, B, C. Diện tích tam giác ABC bằng:
 Xem đáp án
Xem đáp án
Ta có: và có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm
Khi đó ta có:
Gọi p là nửa chu vi tam giác ABC ta có:
Diện tích tam giác ABC là:
Đáp án cần chọn là: D
Câu 7:
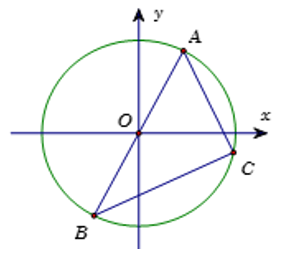
Trong mặt phẳng phức, gọi A, B, C lần lượt là các điểm biểu diễn của các số phức . Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Ta có:
Suy ra trọng tâm của tam giác ABC là suy ra phương án B sai.
Đáp án cần chọn là: B
Câu 9:
Cho số phức với . Gọi (P) là tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng
 Xem đáp án
Xem đáp án
Ta có: được biểu diễn bởi điểm M(x; y) với
Vậy tập hợp điểm biểu diễn số phức z là parabol (P):
Hoành độ giao điểm của parabol (P) với trục hoành là:
Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng:
Đáp án cần chọn là: A
Câu 10:
Tính mô đun của số phức . Biết số phức z có mô đun bằng m
 Xem đáp án
Xem đáp án
Ta có:
vì
Đáp án cần chọn là: A
Câu 11:
Cho các số phức . Số giá trị nguyên của m để là:
 Xem đáp án
Xem đáp án
Ta có:
Mà
Mặt khác
Có 5 giá trị của m thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: B
Câu 13:
Cho số phức . Gọi (C) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (C) và trục hoành bằng:
 Xem đáp án
Xem đáp án
Ta có điểm biểu diễn của số phức z là
là 1 parabol.
Hoành độ giao điểm của đồ thị hàm số với trục hoành là
Diện tích hình phẳng cần tìm là
Đáp án cần chọn là: A
Câu 14:
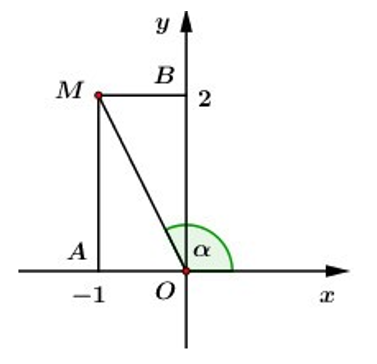
Trên mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn hình học của số phức và là góc lượng giác có tia đầu Ox, tia cuối OM. Tính
 Xem đáp án
Xem đáp án
Ta có: có điểm biểu diễn là
Ta có:
(hai góc bù nhau)
Đáp án cần chọn là: D

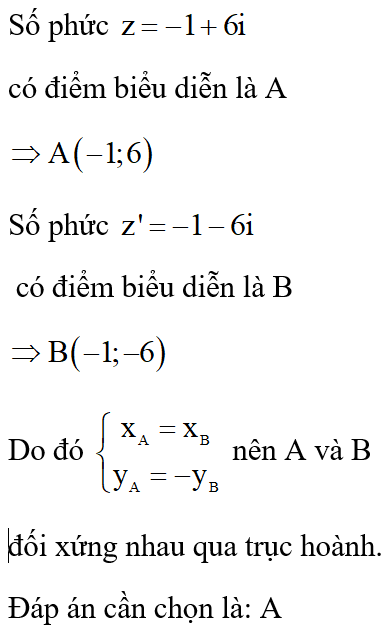
 . Mệnh đề nào sau đây là đúng?
. Mệnh đề nào sau đây là đúng?

