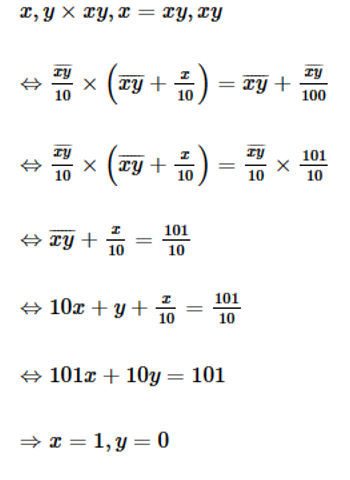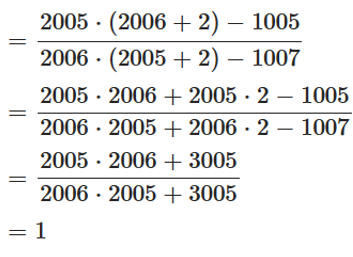Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 6)
-
2011 lượt thi
-
58 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Có bao nhiêu số tự nhiên chẵn có 4 chữ số chia hết cho 9?
 Xem đáp án
Xem đáp án
Các số chẵn có 4 chữ số chia hết cho 9 là: 1008; 1026; ...; 9990.
Số chẵn lớn nhất có 4 chữ số chia hết cho 9 là 9990
Số chẵn bé nhất có 4 chữ số chia hết cho 9 là 1008
Hai số chẵn có 4 chữ số chia hết cho 9 liên tiếp có khoảng cách là:
1026 – 1008 = 18 (đơn vị)
Số số chẵn có 4 chữ số chia hết cho 9 là:
(9990 – 1008) : 18 + 1 = 500 (số)
Vậy có 500 số chẵn có 4 chữ số chia hết cho 9.
Câu 2:
Tập hợp các số nguyên tố nhỏ hơn 10 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Nên các số nguyên tố nhỏ hơn 10 là 2; 3; 5; 7.
Vậy ta chọn đáp án B.
Câu 3:
Một tháng có ba ngày chủ nhật đều là ngày chẵn. Ngày 15 tháng đó là thứ mấy?
 Xem đáp án
Xem đáp án
Do 2 ngày chủ nhật liên tiếp cách nhau 7 ngày nên nếu 3 ngày chủ nhật đều là ngày chẵn thì tháng đó có 5 ngày chủ nhật
Suy ra ngày chủ nhật đầu tiên của tháng là ngày 2 (vì nếu là ngày 4 thì tháng đó sẽ không có ngày chủ nhật thứ năm, vì 4 + 4.7 = 32 > 31)
Do đó các ngày chủ nhật trong tháng là ngày 2; 9; 16; 23; 30
Suy ra ngày 15 là thứ 7
Vậy ngày 15 tháng đó là thứ 7.
Câu 4:
Một người mua một số cam, sau khi bán hết người đó thu được 682 500 đồng. Tính ra người đó lãi được 18% giá bán. Hỏi giá vốn số cam đó là bao nhiêu?
 Xem đáp án
Xem đáp án
Số tiền lãi là:
682 500 : 100 × 18 = 122 850 (đồng)
Số tiền vốn là:
682 500 – 122 850 = 559 650 (đồng)
Vậy giá vốn số cam là 559 650 đồng.
Câu 5:
Tìm một số tự nhiên có hai chữ số, biết rằng nếu ta viết thêm vào bên trái số đó một chữ số 2 thì ta được số mới mà tổng số đã cho và số mới bằng 346.
 Xem đáp án
Xem đáp án
Gọi số phải tìm là
Số mới là
Theo bài ra ta có:
Vậy số phải tìm là 73 .
Câu 6:
Chứng minh rằng tích của 3 số tự nhiên liên tiếp chia hết cho 3.
 Xem đáp án
Xem đáp án
Gọi tích của 3 số liên tiếp là
A = a(a + 1)(a + 2) (a thuộc N*)
+) Nếu a chia hết 3
Suy ra a(a + 1)(a + 2) chia hết cho 3
Hay A chia hết 3.
+) Nếu a không chia hết cho 3 thì có 2 khả năng a chia 3 dư 1 hoặc a chia 3 dư 2
• Trường hợp 1: a chia 3 dư 1 thì a = 3n + 1
Suy ra a + 2 = (3n + 1) + 2 = 3n + 3 chia hết cho 3
Do đó A chia hết 3
• Trường hợp 2: a chia 3 dư 2 thì a = 3n + 2
Suy ra a + 1 = 3n + 2 + 1 = 3n + 3 chia hết cho 3
Do đó A chia hết 3
Vậy tích của 3 số tự nhiên liên tiếp chia hết cho 3.
Câu 7:
Tính bằng cách thuận tiện 649,18 – (25,48 + 49,18) – 74,52.
 Xem đáp án
Xem đáp án
649,18 – (25,48 + 49,18) – 74,52
= 649,18 – 25,48 – 49,18 – 74,25
= (649,18 – 49,18) – (25,48 + 74,52)
= 600 – 100
= 500.
Câu 8:
Tính nhanh: 2 904,02 – 152,36 – 547,64.
 Xem đáp án
Xem đáp án
Ta có:
2 904,02 – 152,36 – 547,64
= 2 904,02 – (152,36 + 547,64)
= 2 904,02 – 700
= 2 204,02.
Câu 9:
Tính diện tích một hình tròn, biết nếu giảm đường kính hình tròn đó đi 20% thì diện tích giảm đi 113,04 cm2.
 Xem đáp án
Xem đáp án
Nếu giảm đường kính hình tròn đi 20% thì bán kính hình tròn đó cũng giảm đi 20%
Khi đó diện tích đường tròn sẽ giảm đi
100% × 100% – (100% – 20%) × (100% – 20%) = 36%
Diện tích hình tròn là:
113,04 : 36 × 100 = 314 (cm2)
Vậy diện tích hình tròn là 314 cm2.
Câu 10:
Tổng của số thứ nhất và số thứ hai là 48,38. Tổng của số thứ hai và số thứ ba là 62,75. Tổng của số thứ nhất và số thứ ba là 62,87. Số thứ ba là bao nhiêu?
 Xem đáp án
Xem đáp án
Tổng của ba số là:
(48,38 + 62,75 + 62,87) : 2 = 87
Số thứ ba là:
87 – 48,38 = 38,62
Số thứ nhất là:
87 – 62,75 = 24,25
Số thứ hai là:
48,38 – 24,25 = 24,13
Vậy số thứ ba là 38,62.
Câu 11:
Vẽ đồ thị của hàm số y = |x – 2|.
 Xem đáp án
Xem đáp án
Xét hàm số y = x – 2
Ta có đường thẳng y = x – 2 đi qua hai điểm (0; –2) và (2; 0)
Vẽ đồ thị hàm số y = x – 2
Vẽ đồ thị hàm số y = |x – 2| bằng cách:
Giữ lại phần đồ thị hàm số y = x – 2 ở phía trên Ox và lấy đối xứng phần đồ thị phía dưới Ox lên phía trên ta được đồ thị hàm số y = |x – 2| như sau:
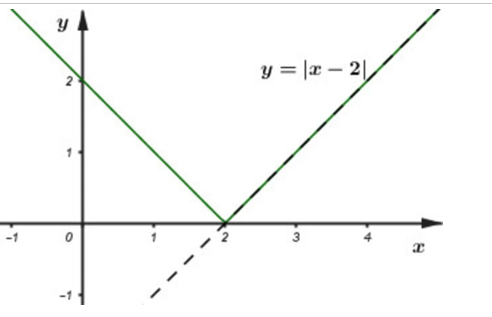
Câu 13:
Một người đi bộ trung bình mỗi phút đi được 73,5 m.
a) Trong giờ người đó đi được bao nhiêu m?
 Xem đáp án
Xem đáp án
a) giờ = 15 phút
Trong giờ người đó đi được là:
73,5 × 15 = 1 102,5 (m)
Câu 14:
b) Trong giờ người đó đi được bao nhiêu km?
 Xem đáp án
Xem đáp án
b) giờ = 24 phút
Trong giờ người đó đi được là:
73,5 × 24 = 1 764 (m) = 1,764 (km).
Câu 15:
Tìm hai số tự nhiên a và b biết BCNN(a, b) – ƯCLN(a, b) = 35.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Gọi ƯCLN(a, b) = d. Suy ra
ƯCLN(m, n) = 1 và m, n ∈ N*
Ta có BCNN(a, b) . ƯCLN(a, b) = ab
Suy ra
Mà BCNN(a, b) – UCLN(a, b) = 35
Do đó mnd – d = 35
Hay d(mn – 1) = 35
Suy ra mn – 1 ∈ Ư(35) = {1; 5; 7; 35}
Hay mn ∈ {2; 6; 8; 36}
+) Với d = 1 thì mn – 1 = 35 hay mn = 36
+) Với d = 5 thì mn – 1 = 7 hay mn = 8

+) Với d = 7 thì mn – 1 = 5 hay mn = 6

+) Với d = 35 thì mn – 1 = 1 hay mn = 2
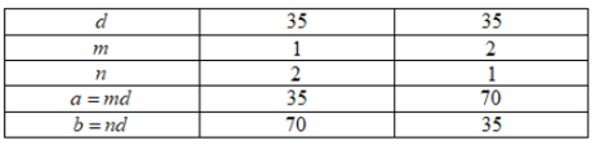
Khi đó ta có các cặp số thỏa mãn là (a; b) ∈ {(1; 36); (36; 1); (4; 9); (9; 4); (5; 40); (40; 5); (7; 42); (42; 7); (14; 21); (21; 14); (35; 70); (70; 35)}
Vậy ta chọn đáp án D.
Câu 16:
Cho hai tập hợp A = {1; 2; 3; 4}, B = {3; 4; 5}. Tìm tất cả các tập hợp M thỏa mãn M ⊂ A và M ∩ B = ∅.
 Xem đáp án
Xem đáp án
Do M ∩ B = ∅ nên M và B là hai tập hợp rời nhau hay mọi phần tử của tập hợp M đều khác các phần tử trong tập hợp B, do đó tập hợp M không chứa các phần tử 3; 4; 5 (1)
Lại có M ⊂ A, do đó mọi phần tử của M đều là phần tử của A nên M có thể chứa các phần tử 1; 2; 3; 4 (2)
Từ (1) và (2) suy ra M chỉ có thể chứa các phần tử 1; 2.
Do đó, M = {1}, M = {2}, M = {1; 2}
Lại có ∅ ⊂ A và ∅ ∩ B = ∅, do đó M = ∅
Vậy các tập hợp M thỏa mãn là: ∅, {1}, {2}, {1; 2}.
Câu 17:
Cho hai hợp tử: A = {1; 2}, B = {3; 4}. Viết các tập hợp gồm hai phần tử, trong đó một phần tử thuộc A, một phần tử thuộc B.
 Xem đáp án
Xem đáp án
Ta có các tập hợp gồm hai phần tử, trong đó một phần tử thuộc A, một phần tử thuộc B là:
C = {1; 3}; D = {1; 4}; F = {2; 3}; E = {2; 4}.
Câu 18:
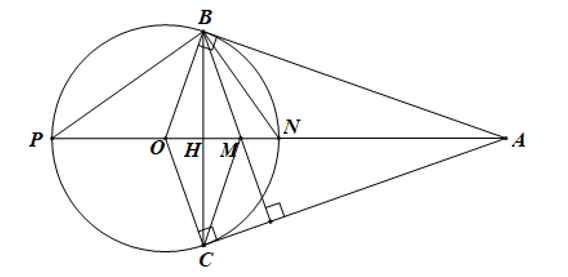
Cho đường tròn (O; R). Từ A nằm ngoài đường tròn kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh bốn điểm A, B, C, O thuộc cùng một đường tròn.
 Xem đáp án
Xem đáp án
a)
Vì AB, AC là tiếp tuyến của (O) nên AB ⊥ OB, AC ⊥ OC
Suy ra
Xét tứ giác ABOC có , mà hai góc này ở vị trí đối nhau
Suy ra tứ giác ABOC nội tiếp
Do đó 4 điểm A, B, O, C cùng nằm trên một đường tròn.
Câu 19:
b) Đường thẳng AO cắt đường tròn (O) tại P và N (N nằm giữa A và P). Chứng minh AN.AP = AB2.
 Xem đáp án
Xem đáp án
b) Xét (O) có lần lượt là góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BN
Suy ra
Xét tam giác PBA và tam giác BNA có
(chứng minh trên)
là góc chung
Suy ra (g.g)
Do đó (tỉ số đồng dạng)
Suy ra AP . AN = AB2.
Câu 20:
c) Khi A di động trên đường tròn (O; 3R), gọi M là trực tâm tam giác ABC. Chứng minh M di động trên một đường tròn cố định.
 Xem đáp án
Xem đáp án
c) Ta có: OC ⊥ CA, BM ⊥ CA nên OC // BM.
Tương tự ta có OB // CM.
Xét tứ giác OBMC có OC // BM và OB // CM nên OBMC là hình bình hành.
Lại có OB = OC nên OBMC là hình thoi.
Do đó OM, BC vuông góc với nhau tại trung điểm của mỗi đường, gọi là H.
Khi đó OM = 2OH.
Xét DOBA có đường cao BH, theo hệ thức lượng ta có:
OB2 = OH.OA, suy ra
Do đó .
Vậy khi A di động trên đường tròn (O; 3R) thì M di động trên đường tròn .
Câu 21:
Bạn Long có một quyển sách 80 trang nhưng vì quyển sách đã cũ nên bị mọt ăn mất một số trang. Các trang bị ăn là: 50; 28; 34; 69. Hỏi quyển sách còn lại bao nhiêu trang?
 Xem đáp án
Xem đáp án
Quyển sách mất trang 50 có nghĩa là mất luôn trang 49.
Quyển sách mất trang 28 có nghĩa là mất trang 27.
Quyển sách mất trang 34 có nghĩa là mất lôn trang 33.
Quyển sách mất trang 69 có nghĩa là mất luôn trang 70.
Vậy quyển sách còn số trang là:
80 – (4 × 2) = 72 (trang)
Vậy quyển sách còn lại 72 trang.
Câu 22:
Một cửa hàng có 12,45 tạ gạo. Cửa hàng đã bán hai lần, mỗi lần 367 kg. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
 Xem đáp án
Xem đáp án
Đổi 12,45 tạ = 1 245 kg
Số kg gạo cửa hàng đã bán là:
367 × 2 = 734 (kg)
Cửa hàng còn lại số kg gạo là :
1 245 – 734 = 511 (kg)
Vậy cửa hàng còn lại 511 kg gạo.
Câu 23:
 Xem đáp án
Xem đáp án
Chu vi hình vuông đó là:
12,36 × 4 = 49,44 (cm)
Vậy chu vi hình vuông là 49,44 cm.
Câu 24:
 Xem đáp án
Xem đáp án
Tổng 10 số tự nhiên liên tiếp đầu tiên là:
0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
= (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 5
= 10 × 4 + 5 = 45.
Câu 25:
Trong đợt khảo sát chất lượng, lớp 10C có 11 học sinh đạt điểm giỏi môn Toán, 8 học sinh đạt điểm giỏi môn Lý, 5 học sinh đạt điểm giỏi cả môn Toán và Lý, 4 học sinh đạt điểm giỏi cả môn Toán và Hóa, 2 học sinh đạt điểm giỏi cả môn Hóa và Lý, 1 học sinh đạt điểm giỏi cả ba môn Toán, Lý, Hóa. Hỏi lớp 10C có bao nhiêu học sinh đạt điểm giỏi môn Hóa, biết trong lớp có 16 học sinh giỏi ít nhất một môn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
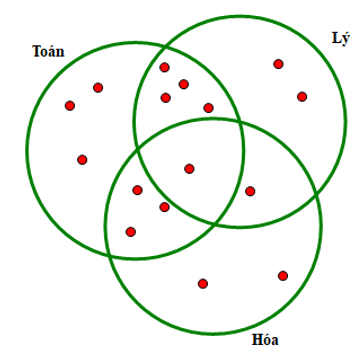
Dựa vào biểu đổ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: 5 – 1 = 4 (em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: 4 – 1 = 3 (em)
Số học sinh chỉ giỏi Hóa và Lý (không giỏi Toán) là: 2 – 1 = 1 (em)
Số học sinh chỉ giỏi một môn Toán là: 11 – 1 – 4 – 3 = 3 (em)
Số học sinh chỉ giỏi một môn Lý là: 8 – 1 – 4 – 1 = 2 (em)
Mà số học sinh giỏi ít nhất một môn là 16 em
Suy ra số học sinh chỉ giỏi một môn Hóa là: 16 – 4 – 3 – 1 – 3 – 2 – 1 = 2 (em)
Khi đó số học sinh giỏi môn Hóa là: 3 + 1 + 1 + 2 = 7 (em)
Vậy ta chọn đáp án A.
Câu 26:
Tìm số có dạng abc sao cho .
 Xem đáp án
Xem đáp án
Vì hàng đơn vị và hàng chục có c + b = c nên b = 0
Hàng trăm có a + a = c nên c = 2a
Vì c là số có 1 chữ số nên ta có các cặp
(a; c) = (1; 2), (a; c) = (2; 4), (a; c) = (3; 6), (a; c) = (4; 8).
Khi đó ta có
102 + 120 = 222
204 + 240 = 444
306 + 360 = 666
408 + 480 = 888
Vậy có 4 số thỏa mãn là 102, 204, 306, 408.
Câu 27:
Một ô tô trong 3 giờ đầu, mỗi giờ đi được 42,8 km. Hai giờ sau, mỗi giờ ô tô đi được 48,3 km. Hỏi trung bình mỗi giờ ô tô đó đi được bao nhiêu km?
 Xem đáp án
Xem đáp án
Trong 3 giờ đầu ô tô đi được số km là:
42,8 × 3 = 128,4 (km)
Trong 2 giờ sau ô tô đi được số km là:
48,3 × 2 = 96,6 (km)
Trung bình mỗi giờ ô tô đi được số km là:
(128,4 + 96,6) : (3 + 2) = 45 (km)
Vậy trung bình mỗi giờ ô tô đi được 45 km.
Câu 29:
Tìm điều kiện của k để N chia hết cho 16 biết N = k4 + 2k3 – 16k2 – 2k + 15.
 Xem đáp án
Xem đáp án
Ta có:
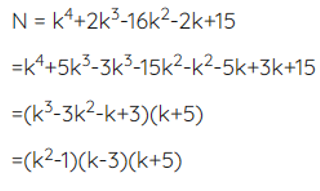
Để N ⋮ 16 thì ta xét các trường hợp:
TH1: N = 0
⇔ (k2 – 1)(k – 3)(k + 5) = 0
TH2: Với k là số lẻ
Ta có k2 – 1 = (k + 1)(k – 1)
Với k là số lẻ thì k – 1 và k + 1 là 2 số chẵn liên tiếp. Trong đó có 1 số chia hết cho 2 và 1 số chia hết cho 4
Suy ra (k – 1)(k + 1) ⋮ 8
Đồng thời, với k lẻ thì k – 1 hoặc k + 5 đều chia hết cho 2
Suy ra N ⋮ 16
Vậy k lẻ thì N chia hết cho 16.
Câu 30:
Một người dùng 760 chữ số để đánh số trang một cuốn sách. Hỏi cuốn sách đó có bao nhiêu trang (cả bìa) biết các trang của bìa không đánh số.
 Xem đáp án
Xem đáp án
Số có 1 chữ số là 3 đến 9 có 7 chữ số
Số có 2 chữ số là 10 đến 99 có 90 số và 180 chữ số
Còn lại 760 – 7 – 180 = 753 chữ số
753 chữ số tương ứng với 191 số có 3 chữ số
số có 3 chữ số từ số 100 đến 290 có 191 chữ số
Vậy trang có 294 trang.
Câu 31:
Cho phân số . Hãy tìm một số sao cho khi đem tử số và mẫu số của phân số đã cho cộng với số đó ta được phân số tối giản .
 Xem đáp án
Xem đáp án
Nếu đem tử số và mẫu số của phân số đã cho cộng với số đó thì hiệu không đổi
Hiệu của tử số và mẫu số ban đầu là: 99 – 29 = 70
Ta có sơ đồ sau:
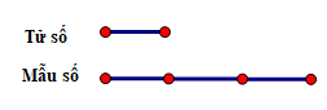
Tử số mới là:
70 : (3 – 1) = 35
Số đó là:
35 – 29 = 6
Vậy số cần tìm là 6.
Câu 32:
Khi xóa 2 chữ số tận cùng của một số ta được số mới kém số đầu 1989 đơn vị. Tìm số tự nhiên đó.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là
Ta có
Mà 1989 : 99 = 20 (dư 9)
Suy ra
Vậy số cần tìm là 2009.
Câu 33:
Tìm số có 2 chữ số, biết rằng số đó gấp 21 lần hiệu của chữ số hàng chục trừ đi chữ số hàng đơn vị.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là
Ta có:
⇔ 10a + b = 21a – 21b
⇔ 11a = 22b
⇔ a = 2b
Suy ra các số thỏa mãn là 21, 42, 63, 84.
Câu 34:
Tính nhanh:
A = 2006 × 2008 – 20072.
 Xem đáp án
Xem đáp án
Ta có:
A = 2006 × 2008 – 20072
A = 2006 × 2008 – 2007 × 2007
A = 2006 × (2007 + 1) – 2007 × (2006 + 1)
A = 2006 × 2007 + 2006 – 2007 × 2006 + 2007
A = 2006 – 2007
A = –1
Câu 35:
Tính nhanh:
B = 2016 × 2018 – 20172.
 Xem đáp án
Xem đáp án
B = 2016 × 2018 – 20172
B = 2016 × 2018 – 2017 × 2017
B = 2016 × (2017 + 1) – 2017 × (2016 + 1)
B = 2016 × 2017 + 2016 – 2017 × 2016 + 2017
B = 2016 – 2017
B = –1.
Câu 37:
S có 128 phần tử, hỏi S có bao nhiêu tập hợp con có 3 phần tử?
 Xem đáp án
Xem đáp án
Mỗi tập con gồm 3 phần tử là một tổ hợp chập 3 của 128 phần tử.
Vậy có tập con.
Câu 38:
Bỏ ngoặc rồi tính: – (12 + 21 – 23) – (23 – 21 + 10).
 Xem đáp án
Xem đáp án
Ta có:
– (12 + 21 – 23) – (23 – 21 + 10)
= –12 – 21 + 23 – 23 + 21 – 10
= (–12 – 10) + (23 – 23) + (21 – 21)
= –24 + 0 + 0
= –24.
Câu 39:
Cho hình chữ nhật ABCD, (M trên AB).
a) Tìm điểm N trên DC sao cho diện tích tứ giác MBCN gấp đôi diện tích tứ MNDA?
 Xem đáp án
Xem đáp án
a)
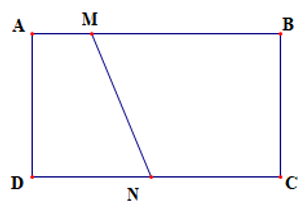
Vì ABCD là hình chữ nhật
Nên AB = CD, AD = BC,
Ta có AB = 4AM = 4 × 3 = 12
Suy ra CD = 12
AM + MB = AB
⇔ 3 + MB = 12
⇔ MB = 9
Ta có:
Vì SMBCN = 2SMNDA
Nên
Mà AD = BC
Suy ra (MB + NC) = 2(MA + ND)
⇔ MB – 2 MA = 2ND – NC
⇔ 9 – 2 × 3 = 2ND – NC
⇔ 3 = 2ND – NC
Mà ND + NC = CD = 12
Suy ra NC = 7, ND = 5
Vậy điểm N trên DC thỏa mãn ND = 5 cm thì diện tích tứ giác MBCN gấp đôi diện tích tứ MNDA.
Câu 40:
b) Với điểm N ở câu a, tính hiệu chu vi hình thang MBCN và MNDA?
 Xem đáp án
Xem đáp án
b) Chu vi hình thang MBCN là
MB + BC + CN + NM = 9 + BC + 7 + MN = AD + MN + 16
Chu vi hình thang MNDA là
AM + MN + ND + DA = 3 + MN + 5 + AD = AD + MN + 8
Suy ra hiệu chu vi hình thang MBCN và MNDA là
AD + MN + 16 – (AD + MN + 8) = 8
Vậy hiệu chu vi hình thang MBCN và MNDA bằng 8 cm.
Câu 41:
Cho đường tròn (O; R), đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax, kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao điểm của CO và AD là I.
a) Chứng minh: CO ⊥ AD.
 Xem đáp án
Xem đáp án
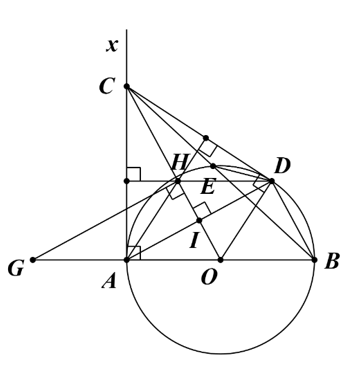
a) Ta có CA, CD là hai tiếp tuyến của (O) cắt nhau tại C
Suy ra CA = CD
Khi đó C nằm trên đường trung trực của đoạn thẳng AD (1)
Lại có OA = OD = R.
Suy ra O nằm trên đường trung trực của đoạn thẳng AD (2)
Từ (1) và (2) suy ra CO là đường trung trực của đoạn thẳng AD
Do đó CO ⊥ AD tại I.
Câu 42:
b) Gọi giao điểm của CB và đường tròn (O) là E (E ≠ B). Chứng minh CE . CB = CI . CO.
 Xem đáp án
Xem đáp án
b) Xét ∆CED và ∆CDB có:
là góc chung
(góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung)
Suy ra (g.g)
Do đó
Suy ra CE . CB = CD2 (3)
Xét ∆CDO vuông tại D có DI là đường cao:
CD2 = CI . CO (hệ thức lượng trong tam giác vuông) (4)
Từ (3) và (4) suy ra CE . CB = CI . CO (điều phải chứng minh).
Câu 43:
c) Chứng minh: Trực tâm H của tam giác CAD di động trên đường cố định khi điểm C di chuyển trên Ax.
 Xem đáp án
Xem đáp án
c) Ta có AH ⊥ CD, OD ⊥ CD
Suy ra AH // OD (quan hệ từ vuông góc đến song song)
Ta có DH ⊥ CA, AO ⊥ CA
Suy ra DH // OA (quan hệ từ vuông góc đến song song)
Xét tứ giác AHDO có
AH // OD, DH // OA (chứng minh trên)
Suy ra tứ giác AHDO là hình bình hành
Mà I là giao điểm của AD và HO
Do đó I là trung điểm của HO
Trên tia đối của tia AO, lấy điểm G sao cho A là trung điểm của GO
Khi đó AI là đường trung bình của tam giác GHO
Suy ra AI // GH
Mà AI ⊥ HO (chứng minh trên)
Do đó GH ⊥ HO
Hay
Vậy khi C di chuyển trên Ax thì trực tâm H của tam giác ACD di động trên đường tròn tâm A, bán kính AO cố định.
Câu 44:
Một kho chứa 246,75 tấn gạo. Người ta chuyển đến một số lượng gạo bằng số gạo hiện có của kho. Hỏi kho đó có tất cả bao nhiêu kg gạo?
 Xem đáp án
Xem đáp án
Số tấn gạo được chuyển đến là:
(tấn)
Số tấn gạo kho có tất cả là:
246,75 + 148,05 = 394,8 (tấn) = 394 800 (kg)
Vậy kho đó có 394 800 kg gạo.
Câu 45:
Một vườn cây hình chữ nhật có diện tích 789,25 m2, chiều dài 38,5 m. Người ta muốn rào xung quanh vườn dài bao nhiêu mét, biết cửa vườn rộng 3,2 m.
 Xem đáp án
Xem đáp án
Chiều rộng vườn cây là:
789,25 : 38,5 = 20,5 (m)
Chu vi vườn cây là:
(38,5 + 20,5) × 2 = 118 (m)
Rào xung quanh vườn dài là:
118 – 3,2 = 114,8 (m)
Vậy rào xung quanh vườn dài 114,8 m.
Câu 46:
Tìm x biết: x4 = 2x2 – 12x + 8.
 Xem đáp án
Xem đáp án
x4 = 2x2 – 12x + 8.
⇔ x4 – 2x2 + 12x – 8 = 0
⇔ (x4 + 2x3 – 2x2) + (–2x3 – 4x2 + 4x) + (4x2 + 8x – 8) = 0
⇔ x2(x2 + 2x – 2) – 2x(x2 + 2x – 2) + 4(x2 + 2x – 2) = 0
⇔ (x2 + 2x – 2)(x2 – 2x + 4) = 0
Vậy hoặc .
Câu 48:
Tìm x, y là số nguyên dương biết:
.
 Xem đáp án
Xem đáp án
Ta có:

Vì x, y là số nguyên dương nên (x – 6)(y – 6) ∈ Ư(37) = {1; 37}
Vậy (x; y) = (7; 42) hoặc (x; y) = (42; 7).
Câu 49:
Cho tích 1 × 2 × 3 × 4 × ... × 100. Hỏi tích tận cùng có bao nhiêu chữ số 0.
 Xem đáp án
Xem đáp án
Ta chú ý đến các thừa số tận cùng bằng 0: 10; 20; 30; 40; 50; 60; 70; 80; 90; 100 và tận cùng bằng 5: 5; 15; 25; 35; 45; 55; 65; 75; 85; 95
Tích 10 × 20 × 30 × 40 × 60 × 70 × 80 × 90 × 100 tận cùng bằng 10 số 0
Tích của 50 và một số chẵn tận cùng bằng 2 chữ số 0
Tích 25 × 4 tận cùng bằng 2 chữ số 0
Tích 75 × 36 tận cùng bằng 2 chữ số 0
Mỗi số 5; 15; 35; 45; 55; 65; 85; 95 nhân với một số chẵn (ngoài những số đã lấy ở trên) cho một số tận cùng bằng 1 chữ số 0
Ngoài ra, không còn có hai thừa số nào cho tích tận cùng bằng 0
Suy ra có 10 + 2 + 2 + 2 + 1 + 1 + 1 + 1 + 1 + 1 + 1+ 1 = 24 chữ số 0
Vậy tích 1 × 2 × 3 × 4 × ... × 100 tận cùng bằng 24 chữ số 0.
Câu 50:
 Xem đáp án
Xem đáp án
Ta có:
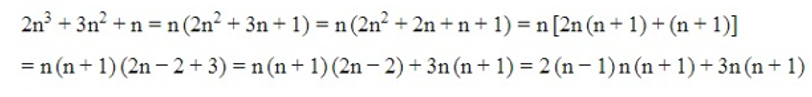
Ta thấy (n – 1), n, (n + 1) là 3 số nguyên liên tiếp
Suy ra (n – 1)n(n + 1) chia hết cho 2 và 3
Do đó 2(n – 1)n(n + 1) ⋮ 6
Có n(n + 1) ⋮ 2
Suy ra 3n(n + 1) ⋮ 6
Do đó 2(n – 1)n(n + 1) + 3n(n + 1) ⋮ 6
Vậy 2n3 +3n2 + n chia hết cho 6 với mọi số nguyên n.
Câu 51:
Tìm các cặp số tự nhiên x, y biết: 6xy – 9x – 4y + 5 = 0.
 Xem đáp án
Xem đáp án
Ta có 6xy – 9x – 4y + 5 = 0
⟺ 6xy – 9x – 4y + 6 – 1 = 0
⟺ 3x(2y – 3) – 2(2y – 3) = 1
⟺ (3x – 2)(2y – 3) = 1
Ta có bảng
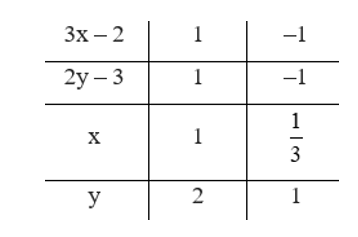
Mà x, y là số tự nhiên, suy ra x = 1, y = 2
Vậy x = 1, y = 2.
Câu 52:
Cho tam giác ABC. Trên tia đối của AB lấy D sao cho AD = AC, trên tia đối của AC lấy E sao cho AE = AB. Gọi M và N lần lượt là trung điểm của BE và CD. Chứng minh 3 điểm M, A, N thẳng hàng.
 Xem đáp án
Xem đáp án
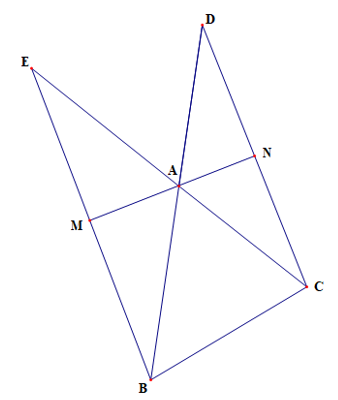
Vì AD = AC nên tam giác ACD cân tại A
Mà AN là trung tuyến
Suy ra AN là phân giác của
Do đó
Vì AE = AB nên tam giác ABE cân tại A
Mà AM là trung tuyến
Suy ra AM là phân giác của
Do đó
Ta có (hai góc đối đỉnh)
Suy ra
Hay
Ta có (hai góc kề bù)
Mà
Suy ra
Hay
Do đó M, A, N thẳng hàng
Vậy 3 điểm M, A, N thẳng hàng.
Câu 53:
Cho tam giác ABC. Trên tia đối của tia AB lấy D sao cho AD = AB, trên tia đối của tia AC lấy điểm E sao cho AE = AC
a) Chứng minh rằng: BE = CD.
 Xem đáp án
Xem đáp án
a)
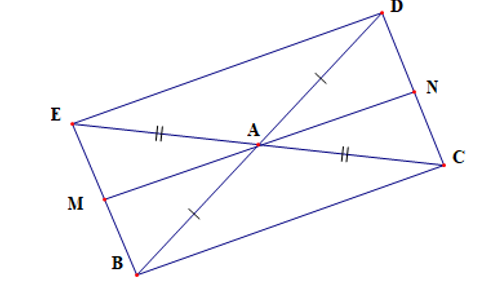
Xét ∆ABE và ∆ADC có:
AB = AD (giả thiết)
AE = AC (giả thiết)
(hai góc đối đỉnh)
Do đó ∆ABE = ∆ADC (c.g.c)
Suy ra BE = CD (2 cạnh tương ứng).
Câu 54:
b) Chứng minh: BE // CD.
 Xem đáp án
Xem đáp án
b) Vì ∆ABE = ∆ADC (chứng minh câu a)
Suy ra (hai góc tương ứng)
Mà 2 góc này ở vị trí so le trong nên BE // CD.
Câu 55:
 Xem đáp án
Xem đáp án
c) Vì BE = CD
nên
suy ra BM = DN
Xét ∆AMB và ∆AND có:
BM = DN (chứng minh trên)
AB = AD (giả thiết)
(chứng minh trên)
Do đó ∆AMB = ∆AND (c.g.c)
Suy ra AM = AN (2 cạnh tương ứng).
Câu 56:
Cho các số thực dương x, y, z thỏa mãn x + y + z = 3. Tìm giá trị nhỏ nhẩ của .
 Xem đáp án
Xem đáp án
Ta có: (x – y)2 + (y – z)2 + (z – x)2 ≥ 0
⇔ x2 – 2xy + y2 + y2 – 2yz + z2 + z2 – 2xz + x2 ≥ 0
⇔ 2x2 – 2xy + 2y2 – 2yz + 2z2 – 2xz ≥ 0
⇔ x2 + y2 + z2 – xy – yz – xz ≥ 0
⇔ x2 + y2 + z2 + 2xy + 2yz + 2xz ≥ 3xy + 3yz + 3xz
⇔ (x + y + z)2 ≥ 3(xy + yz + xz)
Ta có
Suy ra
Dấu “ = ” xảy ra khi x2 = y2 = z2 = 1 hay x = y = 1
Vậy P đạt giá trị nhỏ nhất bằng 3 khi x = y = z = 1.
Câu 57:
Cho x, y, z > 0. Tìm giá trị nhỏ nhất của .
 Xem đáp án
Xem đáp án
Ta có
Áp dụng bất đẳng thức Cô – si ta có
Suy ra A ≥ 3 + 2 + 2 + 2
Hay A ≥ 9
Dấu “ = ” xảy ra khi x = y = z
Vậy A đạt giá trị nhỏ nhất bằng 9 khi x = y = z.
Câu 58:
Cách đây 2 năm mẹ hơn con 28 tuổi. Sau đây 2 năm tuổi con bằng tuổi mẹ. Tính tuổi mẹ và tuổi con hiên nay.
 Xem đáp án
Xem đáp án
Sau 2 năm thì tuổi mẹ vẫn hơn tuổi con 28 tuổi
Ta có sơ đồ sau 2 năm:
Tuổi mẹ: |-----|-----|-----|-----|-----|
Tuổi con: |-----| 28 tuổi
Hiệu số phần bằng nhau là: 5 – 1 = 4 (phần)
Tuổi mẹ hiện nay là:
(28 : 4) × 5 – 2 = 33 (tuổi)
Tuổi con hiện nay là:
33 –28 = 5 (tuổi)
Vậy hiện nay mẹ 33 tuổi, con 5 tuổi