30 câu hỏi trắc nghiệm thuộc 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P2)

Câu 1:

Biết hàm số f(x) xác định trên R và có đạo hàm f’(x) = (x – 1)x²(x + 1)³(x + 2)⁴. Hỏi hàm số có bao nhiêu điểm cực trị?

A. 4

B. 1

C. 2

D. 3

Xem đáp án

Đáp án C.

f’(x) = (x – 1)x²(x + 1)³(x + 2)⁴

Ta thấy phương trình f’(x) = 0 có 2 nghiệm đơn là 1; -1 và có hai nghiệm kép là 0; -2

Từ đó số điểm cực trị là 2.

Câu 2:

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:

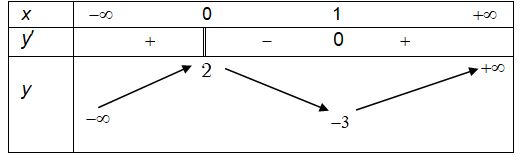
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có đúng một cực trị

B. Hàm số có giá trị cực tiểu bằng 2

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1

Xem đáp án

Đáp án D.

Sử dụng: (Điều kiện đủ để hàm số có cực trị)

- Nếu f’(x) < 0, ∀x ∈(a,x₀) và f’(x) > 0,∀x ∈ (x₀;b) thì đạt cực tiểu tại x₀;

- Nếu f’(x) > 0,∀x ∈ (a;x₀) và f’(x) < 0, ∀x ∈ (x₀;b) thì đạt cực đại tại x₀.

Suy ra hàm số có 2 cực trị và đạt cực đại tại x = 0; đạt cực tiểu tại x = 1

Câu 3:

Cho hàm số y = mx⁴ – (m² – 1)x² + 1. Khẳng định nào sau đây là sai?

A. Với m = 0 thì hàm số có một điểm cực trị

B. Hàm số luôn có 3 điểm cực trị với với mọi m ≤ 0

C. Với m ∈ (-1;0) ∪ (1;+∞) hàm số có 3 điểm cực trị

D. Có nhiều hơn ba giá trị của tham số m để hàm số có 1 điểm cực trị

Xem đáp án

Đáp án B.

Hàm số trùng phương có ba điểm cực trị khi và chỉ khi ab < 0 ó m(1 – m²) < 0

ó m ∈ (-1;0) ∪ (1;+∞).

Vậy phương án B sai.

Câu 4:

Cho các phát biểu sau:

I. Đồ thị hàm số có y = x⁴ – x + 2 có trục đối xứng là Oy.

II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x₀ thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x₀,f(x₀)) song song với trục hoành.

III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b).

IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x₀ thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x₀) và đồng biến trên khoảng (x₀;b).

Các phát biểu đúng là:

A. II,III,IV

B. I,II,III

C. III,IV

D. I,III,IV

Xem đáp án

Đáp án A.

Hàm số có y = x⁴ – x + 2 không là hàm số chẵn nên mệnh đề I sai.

Mệnh đề II, III, IV đúng

Câu 5:

Hàm số nào trong các hàm số sau đây không có cực trị?

A. y = |x|

B. $y = x^{3} - x^{2} + 3 x + 5$

C. $y = x^{4} + x^{2} - 2$

D. $y = 3 x^{2} + 2 x - 1$

Xem đáp án

Đáp án B.

y' = 3x² – 2x + 3 > 0 ∀x ∈ R

Câu 6:

Hàm số y = x⁴ – 4x² + 4 đạt cực tiểu tại những điểm nào?

A. $x = \pm \sqrt{2}, x = 0$

B. $x = \pm \sqrt{2}$

C. $x = \sqrt{2}, x = 0$

D. $x = - \sqrt{2}$

Xem đáp án

Đáp án B

Do a = 1 > 0 nên hàm số đạt cực tiểu tại x = $\pm \sqrt{2}$

Câu 7:

Cho hàm số $y = \frac{1}{3} x^{3} + x^{2} - 7 x + 3$ đạt cực trị tại x₁, x₂. Tính T = x₁³ + x₂³

A. T = -50

B. T = -30

C. T = 29

D. T = 49

Xem đáp án

Đáp án A

Ta có

Khi đó T = x₁³ + x₂³ = -50

Câu 8:

Kết luận nào đúng về cực trị của hàm số y = x³ – 3x² + 3x + 4

A. Đạt cực đại tại x = 1

B. Có hai điểm cực trị

C. Đạt cực tiểu tại x = 1

D. Không có cực trị

Xem đáp án

Đáp án D.

Ta có y’ = 3(x – 1)² ≥ 0, ∀x ∈ R

Câu 9:

Hàm số y = x – sin 2x + 3. Chọn khẳng định đúng trong các khẳng định sau?

A. Nhận điểm x = -π/6 làm điểm cực tiểu

B. Nhận điểm x = π/2 làm điểm cực đại

C. Nhận điểm x = -π/6 làm điểm cực đại

D. Nhận điểm x = π/2 làm điểm cực tiểu

Xem đáp án

Đáp án C

Câu 10:

Hàm số y = x³ – 3x² + 3x – 4 có bao nhiêu cực trị?

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án A

Ta có: y’ = 0 $\Leftrightarrow$ 3x² – 6x + 3 ≥ 0 với mọi x

Nên hàm số đã cho luôn đồng biến trên R.

Vậy hàm số đã cho không có cực trị

Câu 11:

Cho hàm số y = -x³ + 3x² – 3x + 1, mệnh đề nào sau đây là đúng?

A. Hàm số đạt cực đại tại x = 1

B. Hàm số luôn luôn nghịch biến

C. Hàm số luôn luôn đồng biến

D. Hàm số đạt cực tiểu tại x = 1

Xem đáp án

Đáp án B.

Tập xác định D = R.

y' = -3x² + 6x – 3 = -3(x – 1)² ≤ 0, ∀x ∈ R .Vậy hàm số luôn nghịch biến trên R

Câu 12:

Số điểm cực đại của đồ thị hàm số y = x⁴ + 100 là:

A. 1.

B. 3.

C. 0.

D. 2.

Xem đáp án

Đáp án C.

y' = 4x³, y’’ = 12x² ≥ 0 với mọi x nên không có giá trị nào của x để y '' < 0

=> hàm số không có cực đại

Câu 13:

Tìm x_CĐ (nếu có) của hàm số $y = \sqrt{x - 3} - \sqrt{6 - x}$

A. $x_{C Đ}$ = 3

B. $x_{C Đ}$ = 6

C. $x_{C Đ}$ = 0

D. Hàm số không có điểm cực đại

Xem đáp án

Đáp án D

Nên hàm số không có cực đại

Câu 14:

Cho hàm số $y = \frac{- x^{2} + 3}{x - 2}$ . Mệnh đề nào dưới đây đúng?

A. Cực tiểu của hàm số bằng -2

B. Cực tiểu của hàm số bằng 3

C. Cực tiểu của hàm số bằng 1

D. Cực tiểu của hàm số bằng -6

Xem đáp án

Đáp án C.

TXĐ: D = R \ {2}

Câu 15:

Tìm số điểm cực trị của hàm số y = x⁴ + 2x² + 3

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án B.

Tập xác định D = R.

y' = 4x³ + 4x

y’ = 0 <=> 4x³ + 4x = 0 <=> x = 0.

Bảng biến thiên

Câu 16:

Hàm số y = x – sin 2x đạt cực đại tại các điểm nào cho dưới đây?

A. x = -π/3 + kπ, k ∈ Z.

B. x = π/3 + kπ, k ∈ Z.

C. x = π/6 + kπ, k ∈ Z.

D. x = -π/6 + kπ, k ∈ Z.

Xem đáp án

Đáp án D.

Tập xác định: D = R

Ta có y’ = 1 – 2cos 2x

y’ = 0 ó 2x = ±π/3 + k2π $\Leftrightarrow$ x = ±π/6 + kπ, k ∈ Z

y’’ = 4sin 2x.

Khi đó:

y’’(π/6 + kπ) = 4sin(π/3 + k2π) = 2√3 > 0;

y’’(-π/6 + kπ) = 4sin(-π/3 + k2π) = -2√3

Vậy hàm số đạt cực đại tại x = - π/6 + kπ, k ∈ Z

Câu 17:

Cho hàm số $y = \frac{x^{2} - 4 x + 8}{x - 2}$ . Số điểm cực trị của hàm số là

A. 0.

B. 1.

C. 3.

D. 2.

Xem đáp án

Đáp án D.

Tập xác định D = R \ {2}

Bảng biến thiên

Dựa vào bảng biến thiên, số điểm cực trị của hàm số đã cho là 2

Câu 18:

Tọa độ điểm cực đại của đồ thị hàm số y = x³ – 3x² + 4 là:

A. (2;4)

B. (2;0)

C. (0;-4)

D. (0;4)

Xem đáp án

Đáp án D.

+ TXĐ: D = R

+ y’ = 3x² – 6x

Dựa vào bảng biến thiên ta thấy tọa độ điểm cực đại của đồ thị hàm số là (0;4)

Câu 19:

Đồ thị của hàm số y = 3x⁴ – 4x³ – 6x² + 12x + 1 đạt cực tiểu tại M(x₁; y₁). Tính tổng x₁ + y₁

A. 5

B. -11

C. 7

D. 6

Xem đáp án

Đáp án B.

Ta có: y’ = 12x³ – 12x² – 12x + 12.

Bảng biến thiên

=> M(-1;-10) => x₁ + y₁ = -11

Câu 20:

Tìm độ dài khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = x³ + 3x² – 4?

A. $2 \sqrt{5}$

B. $4 \sqrt{5}$

C. $6 \sqrt{5}$

D. $8 \sqrt{5}$

Xem đáp án

Đáp án A

Câu 21:

Đồ thị của hàm số y = 3x⁴ – 4x³ – 6x² + 12x + 1 đạt cực tiểu tại M(x₁; y₁). Khi đó x₁ + y₁ bằng

A. 5

B. 6

C. -11

D. 7

Xem đáp án

chọn C.

y = 3x⁴ – 4x³ – 6x² + 12x + 1 => y’ = 12x³ – 12x² – 12x + 12

y’ = 0 ó 12x³ – 12x² – 12x + 12 = 0

bảng biến thiên

Vậy hàm số y = 3x⁴ – 4x³ – 6x² + 12x + 1 đạt cực tiểu tại M(-1;-10). Khi đó x₁ + y₁ = -11

Câu 22:

Đồ thị hàm số y = ax³ + bx² + cx + d có hai điểm cực trị A(0;0), B(1;1) thì các hệ số a, b, c, d có giá trị lần lượt là:

A. a = -2; b = 1; c = 0; d = 0

B. a = 0; b = 0; c = -2; d = 3

C. a = -2; b = 0; c = 3; d = 0

D. a = -2; b = 3; c = 0; d = 0

Xem đáp án

Đáp án D

Câu 23:

Điểm cực đại của đồ thị hàm số y = x³ + 3x² + 2 là

A. (2;0).

B. (0;2).

C. (-2;6).

D. (-2;-18).

Xem đáp án

Đáp án C.

y = x³+ 3x²+ 2 suy ra y’ = 3x² + 6x; y’’ = 6x + 6

Vậy điểm cực đại của đồ thị hàm số là (-2;6).

Câu 24:

Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số y = (x + 1)(x – 2)²

A. $5 \sqrt{2}$

B. 2

C. $2 \sqrt{5}$

D. 4

Xem đáp án

Đáp án C.

y = (x + 1)(x – 2)².

y' = 3x² – 6x

Khoảng cách giữa hai điểm cực trị AB = $2 \sqrt{5}$

Câu 25:

Tìm tất cả giá trị của m để hàm số y = 1/3.x³ – mx² + (m² – m + 1)x + 1 đạt cực đại tại x = 1

A. m = -2

B. m = -1

C. m = 2

D. m = 1

Xem đáp án

Câu 26:

Đồ thị hàm số y = x⁴ – 3x² + ax + b có điểm cực tiểu A(2;-2). Tính tổng (a + b)

A. -14

B. 14

C. -20

D. 34

Xem đáp án

Đáp án B.

y = x⁴ – 3x² + ax + b => y’ = 4x³ – 6x + a => y’’ = 12x² – 6x

Hàm số có điểm cực tiểu A(2;-2)

Câu 27:

Cho hàm số $y = \frac{x^{2} + 3}{x - 1}$ Khẳng định nào sau đây là đúng?

A. Hàm số đạt cực tiểu tại x = -1

B. Hàm số có hai cực trị $y_{C Đ} < y_{C T}$

C. Hàm số đạt cực đại tại x = 3

D. Giá trị cực tiểu bằng -2

Xem đáp án

Đáp án B

Ta có bảng biến thiên

Hàm số có hai cực trị y_CĐ < y_CT.

Câu 28:

Cho hàm số y = x³/3 – 2x² + 3x + 2/3. Toạ độ điểm cực đại của đồ thị hàm số là

A. (-1;2)

B. (3;2/3)

C. (1;-2)

D. (1;2)

Xem đáp án

Đáp án D.

Tập xác định D = R.

Ta có y’ = x² – 4x + 3, y’ = 0

Bảng biến thiên

Tọa độ điểm cực đại của hàm số là (1;2).

Câu 29:

Giá trị lớn nhất của hàm số $y = \sqrt{- x^{2} + 4 x}$ là:

A. 4

B. 0

C. -2

D. 2

Xem đáp án

Đáp án D.

Câu 30:

Hàm số $y = \frac{x^{2} - 4 x + 1}{x + 1}$ có hai điểm cực trị là x₁, x₂ khi đó tích x₁x₂ bằng

A. -5.

B. 5.

C. -2.

D. 2.

Xem đáp án

Chọn A.

Ta có:

CHỌN BỘ SÁCH BẠN MUỐN XEM

250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số

250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương