256 Bài tập Hàm số mũ và Logarit cực hay có lời giải chi tiết (P1)
-
1172 lượt thi
-
50 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Biết phương trình
có một nghiệm dạng trong đó a,b là các số nguyên. Tính 2a + b.
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng tính đơn điệu của hàm số để giải phương trình.
Cách giải:
ĐKXĐ: x > 1
Ta có:
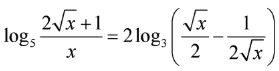
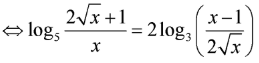
![]()
![]()
![]()
![]()
Xét hàm số ,
có:
Hàm số đồng biến trên
Khi đó, phương trình
![]()
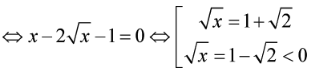
![]()
![]()
Chọn B.
Câu 2:
Số nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Phương pháp:
Cách giải:
Ta có:
Vậy phương trình đã cho có 2 nghiệm là:
Chọn D
Câu 3:
Phương trình có hai nghiệm (với ). Tính giá trị của biểu thức
 Xem đáp án
Xem đáp án
Phương pháp:
.
Cách giải:
ĐKXĐ: x > 0
Ta có:
![]()
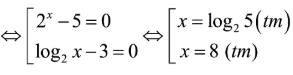
Do phương trình có 2 nghiệm với nên
Chọn C.
Câu 5:
Anh Nam mới ra trường và đi làm với mức lương khởi điêm là 6 triệu đồng/ltháng. Anh muốn dành một khoản tiền tiết kiệm bằng cách trích ra 20% lương hàng tháng gửi vào ngân hàng theo hình thức lãi kép với lãi suất 0,5%/ tháng. Hỏi sau một năm, số tiền tiết kiệm của anh Nam gần nhất với số nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp:
Bài toán: Mỗi tháng đều gửi một số tiền là a triệu đồng vào đầu mỗi tháng tính theo lại kép với lãi suất là
r% mỗi tháng. Số tiền thu được sau n tháng là:
Cách giải:
Số tiền anh Nam gửi mỗi tháng là: 6.20% = 1,2 (triệu đồng)
Sau 1 năm, số tiền tiết kiệm của anh Nam là:
(triệu đồng)
Chọn C.
Câu 6:
Sau một tháng thi công dãy phòng học của Trường X, công ty xây dựng đã thực hiện được một khối lượng công việc. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 25 tháng nữa công trình sẽ hoàn thành. Để kịp thời đưa công trình vào sử dụng, công ty xây dựng quyết định từ tháng thứ 2 , mỗi tháng tăng 5% khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn thành ở tháng thứ mấy sau khi khởi công?
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức:
Cách giải:
Theo kế hoạch, mỗi tháng, công ti đó làm được công việc
Do kê từ tháng thứ 2, mỗi tháng tăng 5% khối lượng công việc so với tháng kề trước, nên lượng công việc công ti đó hoàn thành ở tháng thứ k là:
Gọi là số tháng đê công trình được hoàn thành. Khi đó, là giá trị nguyên dương nhỏ nhất của n, thỏa mãn:
![]()
![]()
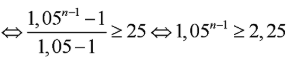
![]()
Vậy sau 18 tháng, công trình sẽ được hoàn thành.
Chọn B.
Câu 7:
Tìm tập xác định của hàm số
 Xem đáp án
Xem đáp án
Phương pháp:
Hàm số xácđịnh
Hàm số ln f (x) xác định
Cách giải:
ĐKXĐ:
TXĐ:
Chọn: A
Câu 8:
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm phân biệt?
 Xem đáp án
Xem đáp án
Phương pháp:
Giải phương trình bằng phương pháp xét hàm số.
Cách giải:
Điều kiện:
Ta có: ![]()
![]()
![]()
![]()
Phương trình (1) có 2 nghiệm thực phân biệt
Phương trình (2) có 2 nghiệm thực phân biệt lớn hơn 1 (*)
Xét hàm số
có
(*) .
Mà : có 3 giá trị của m thỏa mãn.
Câu 9:
Tập giá trị của hàm số là
 Xem đáp án
Xem đáp án
Phương pháp
Hàm số mũ luôn nhận giá trị dương với mọi .
Cách giải:
Ta có: nên tập giá trị của hàm số là .
Chọn B.
Chú ý: Cần phân biệt tập giá trị và tập xác định của hàm số. Hàm số là và TXĐ là .
Câu 10:
Tập xác định của hàm số là
 Xem đáp án
Xem đáp án
Phương pháp
Hàm số với có ĐK:
Cách giải:
ĐK: . Suy ra
Chọn B.
Câu 11:
Tập nghiệm của bất phương trình là
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng các giải bất phương trình: Với a >1 thì
Cách giải:
Ta có ![]()
![]()
Vậy tập nghiệm bất phương trình là
Chọn A.
Câu 12:
Tích tất cả các nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Phương pháp
- Đặt đưa về phương trình bậc hai ẩn t.
- Tìm mối quan hệ giữa các nghiệm x của phương trình đầu với các nghiệm t tương ứng của phương trình sau và tính toán.
Cách giải:
Điều kiện: x > 0 .
Đặt phương trình trở thành
Có ac =1.(-7) = -7 < 0 nên phương trình luôn có hai nghiệm phân biệt thỏa mãn
Do đó phương trình đã cho luôn có hai nghiệm phân biệt
Khi đó
Vậy tích các nghiệm của phương trình đã cho bằng 9 .
Chọn A.
Câu 13:
Cho và . Tính
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng các công thức
(với điều kiện các log có nghĩa)
Cách giải:
Ta có ![]()
![]()
Chọn B.
Câu 14:
Gọi S là tập hợp tất cả các giá trị của tham số và phương trình
=có nghiệm duy nhất. Tìm số phân tử của S .
 Xem đáp án
Xem đáp án
Phương pháp:
- Tìm điều kiện xác định.
- Giải phương trình tìm nghiệm và tìm điều kiện để phương trình có nghiệm duy nhất.
Cách giải:
Điều kiện:
Khi đó, phương trình
Do đó phương trình có nghiệm duy nhất nếu nó chỉ có duy nhất nghiệm hoặc .
TH1: là nghiệm và không là nghiệm.
Khi đó hay không có giá trị nào của m để phương trình nhận làm nghiệm duy nhất.
TH2: là nghiệm và không là nghiệm.
Khi đó
Do đó với thì phương trình đã cho có nghiệm duy nhất .
Mà nên m = 2 hoặc m = 3.
Vậy có hai giá tị của m thỏa mãn bài toán.
Chọn A.
Câu 15:
Tìm tất cả các giá trị của tham số m để phương trình có đúng 2 nghiệm phân biệt thuộc khoảng (0;1).
 Xem đáp án
Xem đáp án
Chọn đáp án A
Phương pháp
+) Tìm điều kiện xác định của phương trình.
+) Đặt ẩn phụ để giải phương trình. Phương trình đã cho có hai nghiệm phân biệt thuộc phương trình ẩn t có hai nghiệm phân biệt thuộc .
Cách giải
Điều kiện: .
Đặt
Khi đó ta có phương trình:
![]()
![]()
(*)
Phương trình đã cho có hai nghiệm phân biệt thuộc phương trình ẩn t có hai nghiệm phân biệt thuộc .
Xét hàm số: trên ta có:
.
Để phương trình (*) có 2 nghiệm phân biệt thuộc thì đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt thuộc .
Câu 16:
Rút gọn biểu thức (với a>0 và a khác 1)
 Xem đáp án
Xem đáp án
Chọn đáp án A
Phương pháp
Sử dụng các công thức .
Cách giải
Câu 17:
Mệnh đề nào sau đây Sai?
 Xem đáp án
Xem đáp án
Chọn đáp án D
Phương pháp
Sử dụng các tính chất của hàm mũ để chọn đáp án đúng.
Cách giải
Ta có: đáp án A đúng.
đáp án B đúng.
đáp án C sai.
Đáp án D đúng.
Câu 18:
Cho biết , khẳng định nào sau đây Đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án A
Phương pháp
Giải bất phương trình lũy thừa:
.
Cách giải
Ta có:
.
Câu 19:
Cho và . Tìm giá trị của biểu thức .
 Xem đáp án
Xem đáp án
Chọn đáp án B
Phương pháp
Giải hệ phương trình logarit và áp dụng bất đẳng thức trị tuyệt đối.
Cách giải
Điều kiện: .
Theo đề bài ta có hệ phương trình:
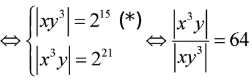
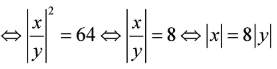
Thay vào (*) ta có
Khi đó ta có
Câu 20:
Tìm hàm số đồng biến trên R.
 Xem đáp án
Xem đáp án
Chọn đáp án A
Phương pháp
Hàm số có TXĐ .
+) Nếu Hàm số đồng biến trên .
+) Nếu Hàm số nghịch biến trên .
Cách giải
Xét hàm số có TXĐ và Hàm số đồng biến trên .
Câu 21:
Cho hai số thực dương x, y thỏa mãn . Tìm giá trị lớn nhất của biểu thức sau:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Phương pháp
+) Sử dụng , chia cả 2 vế cho , tìm mối quan hệ giữa x và y.
+) Thế x theo y vào biểu thức P, đưa P về dạng . Tìm GTLN của .
Cách giải
![]()
![]()
![]()
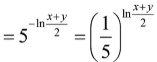
![]()
![]()
Khi đó ta có:
ĐK: .
Xét hàm số , sử dụng MTCT ta tìm được
Vậy .
Câu 22:
Tìm tập xác định D của hàm số
 Xem đáp án
Xem đáp án
Chọn đáp án C
Phương pháp
Hàm số lũy thừa
có TXĐ phụ thuộc vào n như sau:
Cách giải
Ta có: Hàm số xác định
.
Vậy .
Câu 23:
Cho biết , tính giá trị biểu thức
 Xem đáp án
Xem đáp án
Chọn đáp án C
Phương pháp
Sử dụng công thức ().
Cách giải
Ta có:
![]()
![]()
Câu 29:
Một người gửi tiết kiệm ngân hàng với lãi suất 0,5% mỗi tháng theo cách sau: mỗi tháng (vào đầu tháng) người đó gửi vào ngân hàng 10 triệu đồng và ngân hàng tính lãi suất (lãi suất không đổi) dựa trên số tiền tiết kiệm thực tế của tháng đó. Hỏi sau 5 năm, số tiền của người đó có được gần nhất với số tiền nào dưới đây (cả gốc và lãi, đơn vị triệu đồng)?
 Xem đáp án
Xem đáp án
Chọn đáp án A
Tiền thu được cuối mỗi tháng là:
• Tháng 1: .
• Tháng 2
![]()
![]()
…
• Tháng 60:
(triệu đồng)
Câu 30:
Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm.
 Xem đáp án
Xem đáp án
Chọn đáp án A
ycbt có nghiệm
có nghiệm.
Khảo sát , ta có bảng biến thiên:
Từ bảng biến thiên suy ra .
Câu 31:
Tìm tất cả các giá trị thực của tham số m để phương trình có hai nghiệm thỏa .
 Xem đáp án
Xem đáp án
Đáp án B
Câu 33:
Giả sử phương trình có hai nghiệm thực phân biệt thỏa mãn . Giá trị của biểu thức là
 Xem đáp án
Xem đáp án
Chọn đáp án C
Phương pháp
+) Đặt điều kiện để phương trình có nghĩa.
+) Đặt ẩn phụ để giải phương trình: . Tìm điều kiện để phương trình có nghiệm.
+) Dựa vào dữ kiện tìm m. Từ đó tính .
Cách giải
Điều kiện: .
Đặt . Khi đó ta có phương trình:
(*)
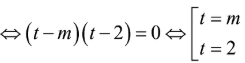
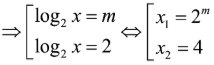
Phương trình đã cho có hai nghiệm phân biệt:
có hai nghiệm phân biệt .
Ta có:
(tm).
.
Câu 34:
Trong hình dưới đây, điểm B là trung điểm của đoạn thẳng AC. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án B
Phương pháp
B là trung điểm AC
Cách giải
Dựa vào đồ thị hàm số ta thấy: A, B, C.
.
Lại có B là trung điểm của AC
Câu 35:
Một người nhận hợp đồng dài hạn làm việc cho một công ty với mức lương khởi điểm của mỗi tháng trong 3 năm đầu tiên là 6 triệu đồng/tháng. Tính từ ngày đầu tiên làm việc, cứ sau đúng 3 năm liên tiếp thì tăng lương 10% so với mức lương một tháng người đó đang hưởng. Nếu tính theo hợp đồng thì tháng đầu tiên của năm thứ 16 người đó nhận được mức lương là bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Phương pháp
Sử dụng công thức: với:
A là số tiền lương tháng đầu tiên người đó nhận được.
r là số % lương người đó được tăng.
n là kì hạn người đó được tăng lương.
Cách giải
Đến năm thứ 16 thì người đó được tăng lương số lần là: lần.
Áp dụng công thức:
ta có số tiền người đó nhận được ở tháng đầu tiên của năm thứ 16 là:
triệu đồng.
Câu 36:
Với x là số thực dương tùy ý, giá trị của biểu thức ln(10x)-ln(5x) bằng
 Xem đáp án
Xem đáp án
Đáp án D
.
Câu 39:
Tổng tất cả các nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Đáp án C
ĐK: và .
Ta có
![]()
![]()
Trường hợp , phương trình tương đương:
![]()
![]()
Nhận nghiệm
Trường hợp , phương trình tương đương:
Nhận nghiệm tổng hai nghiệm bằng .
Câu 40:
Cho các số thực dương a, b thỏa mãn . Đặt T=b/a. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Giả sử , ta có
Thế (1), (2) và (3) ta được phương trình:
.
Vậy
Mà Do đó
Câu 41:
Cho phương trình , với a là tham số thực. Biết phương trình có nghiệm x=2. Giá trị của a bằng
 Xem đáp án
Xem đáp án
Chọn D
.
Vì phương trình có nghiệm nên .
Vậy .
Câu 44:
Tập nghiệm của bất phương trình là
 Xem đáp án
Xem đáp án
Chọn C
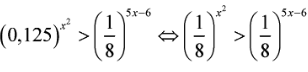 .
.
![]()
Vậy tập nghiệm của bất phương trình đã cho là .
Câu 45:
Ông A vay ngân hàng 200 triệu đồng với lãi suất 1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng theo cách sau: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ, hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ mỗi tháng là như nhau. Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó và sau đúng hai năm kể từ ngày vay ông A trả hết nợ. Hỏi số tiền mỗi tháng ông ta cần trả cho ngân hàng gần nhất với số tiền nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn D
Vay vốn trả góp: Vay ngân hàng số tiền là đồng với lãi suất trên tháng. Sau đúng một tháng kể từ ngày vay, bắt đầu hoàn nợ; hai lần hoàn nợ cách nhau đúng một tháng, mỗi tháng hoàn nợ số tiền là X đồng và trả hết số tiền nợ sau đúng n tháng.
Cách tính số tiền còn lại sau n tháng là:
Chứng minh
Gọi X là số tiền phải trả hàng tháng
- Cuối tháng thứ nhất số tiền nợ là: . Đã trả X đồng nên còn nợ:
- Cuối tháng thứ hai, còn nợ:
- Cuối tháng thứ ba, còn nợ:
…………….
- Cuối tháng thứ n, còn nợ:
Từ đó ta có công thức tổng quát số tiền còn nợ sau n tháng là
Để sau đúng n tháng trả hết nợ thì
Khi đó:
Theo đề ta có 2 năm ứng với 24 tháng:
Vậy số tiền mỗi tháng ông A cần phải trả nợ cho ngân hàng là:
triệu đồng.
Câu 46:
Tổng tất cả các nghiệm của phương trình bằng
 Xem đáp án
Xem đáp án
Chọn B
Ta có
(1)
Đặt ta có PT (1) trở thành
Với ta có
Với ta có
. Do đó tổng tất cả các nghiệm bằng
![]()
![]()
Câu 49:
Cho phương trình . Phương trình đã cho có bao nhiêu nghiệm thực?
 Xem đáp án
Xem đáp án
Chọn C
Điều kiện . Khi đó phương trình đã cho tương đương
Vậy phương trình đang xét có 2 nghiệm thực.
Câu 50:
Tính tích các nghiệm thực của phương trình bằng
 Xem đáp án
Xem đáp án
Chọn A
Bài này không thể nào đưa được về cùng cơ số rồi các em. Bài này rơi vào dạng logarit hóa. Có thể lấy logarit theo cơ số 2 hoặc 3. Tuy nhiên qua sát đáp án là logarit cơ số 2. Do đó ta nghĩ đến việc lấy logarit hai vế của phương trình theo cơ số 2.
Phương trình
![]()
![]()
(*). Gọi là các nghiệm của phương trình (*)
Khi đó